750.1 Open Channels
Contents
- 1 750.1.1 Types of Open Channel Flow
- 2 750.1.2 Kinds of Open Channels
- 3 750.1.3 Continuity and Energy in Open Channel Flow
- 4 750.1.4 Uniform Flow Calculations
- 5 750.1.5 Design of Non-Erodible Channels
- 5.1 750.1.5.1 General Considerations
- 5.2 750.1.5.2 Instructions for the Use of Trapezoidal Channel Charts
- 5.3 750.1.5.3 Instructions for Use of Trapezoidal and Triangular Channel Charts
- 5.4 750.1.5.4 Instructions for Use of Pipe Flow Charts
- 5.5 750.1.5.5 Instructions for Use of Rectangular Channel Charts
- 6 750.1.6 Design of Channels with Flexible Linings
750.1.1 Types of Open Channel Flow
Open channel flow may be classified into several different types. Flow in an open channel is said to be steady if the discharge is constant with respect to time. If the discharge is increasing or decreasing with time, the flow is said to be unsteady. In general, all open channel flow encountered in highway drainage problems is unsteady. That is, the flow rate in these channels will vary with time. Design, however, must be based on the "worst" condition to be expected within a reasonable period of time. This worst condition is the peak flow rate produced by the selected design frequency. Therefore, in design, the time dependent variations of open channel flow are ignored and the channel is assumed to be operating in a steady state.
Steady state flow may be divided into two subgroups; these are: uniform flow and varied flow. Steady state uniform flow is the primary type of flow considered in open channel hydraulics and is the only type of flow to be treated in depth in this guidance on open channel flow. Channel design is based on analysis assuming uniform open channel flow. Varied flow may be subdivided into two classes as gradually varied or rapidly varied. Rapidly varied flow may take the form of either a hydraulic drop or a hydraulic jump. The hydraulic jump has some applications in reducing the velocity of flow and will be discussed in EPG 750.6 Erosion Control and Energy Dissipation.
The flow rate in a channel may also vary along the length of the channel. This type of flow is known as spatially varied open channel flow. That is, the flow rate varies in space. In general, all open channel flow occurring during a runoff event is spatially varied. The best example of spatially varied flow in highway drainage design applications is the flow in a street gutter. Here the flow rate varies from zero at the high point of the pavement, to a maximum at the first down-stream inlet. The spatial variations of open channel flow are considered in the design of some highway drainage facilities.
750.1.2 Kinds of Open Channels
Open channels may be grouped as natural and artificial. This chapter is mainly concerned with the design of artificial channels; however, procedures for the analysis of natural channels are similar.
Open channels may also be classified as to their use, such as roadside channels or storm sewers. All roadside channels, median channels, and street gutters are analyzed and designed as open channels. In general, most storm sewer and sanitary sewer system design is based on open channel flow computations. Culverts may be considered to be a type of open channel. However, culverts do not operate as open channels during the design event and are therefore not designed by the mathematical models of open channel hydraulics. The outlet velocity of culverts may, however, be estimated by open channel flow computations.
750.1.3 Continuity and Energy in Open Channel Flow
Steady state open channel flow is governed by the principles of conservation of mass and conservation of energy.
750.1.3.1 Continuity Equation
The principle of conservation of mass may be expressed by the continuity equation as follows:
- or
- where:
- Q = the flow rate, ft3/s
- A = cross-sectional area of flow, ft2
- V = velocity of flow, ft/s. The subscripts 1 and 2 denote two sections along the channel reach
The above equations apply to all steady state flow. When the flow is also uniform, the area and the velocity at all sections are equal; i.e., A1 = A2 and V1 = V2.
750.1.3.2 Energy Equation
The principle of conservation of energy states that the energy at an upstream section of a channel is equal to the energy at a downstream section of the channel plus the energy required to overcome friction between these two sections. This principle may be expressed by the energy equation.
- where:
- hL = energy loss between Sections 1 and 2, ft
- Z1 and Z2 = elevation head at Sections 1 and 2, respectively, ft
- d1 and d2 = depth of flow at Sections 1 and 2, respectively, ft
- a = a velocity distribution coefficient which may be assumed equal to 1.15 for fairly straight prismatic channels
- V1 and V1 = mean velocity of flow at Sections 1 and 2, respectively, ft/s
- g = 32.2 ft/s2
Steady state uniform open channel flow, hereafter referred to as uniform flow, exists between two sections of a channel when the depth, area, and velocity of flow between these two sections are constant. In order for these conditions to be met, the channel must be of constant cross section, constant roughness, and constant slope for a length sufficient to establish the uniform conditions. When uniform flow exists, the slope of the total energy line, the slope of the water surface profile and the slope of the channel bottom will all be equal.
750.1.4 Uniform Flow Calculations
Various formulas have been developed for calculating the mean velocity in an open channel operating under uniform conditions. These formulas are referred to as uniform flow formulas. The most commonly used uniform-flow formula was presented by Robert Manning in 1889. This formula has almost universal acceptance and is to be used for all open channel design.
750.1.4.1 Manning's Formula
The Manning Equation is expressed as follows:
- where:
- K1 = constant =1.49 English
- V = mean velocity of flow, ft/s
- n = a roughness coefficient
- R = hydraulic radius of the channel cross-section, ft
- S = slope of the channel bottom, ft/ft
A nomograph for the solution of the Manning Equation is available.
750.1.4.1.1 Manning's n
The n value to be used in the above equation is a function of the type of material from which the channel is constructed. The table of n values is used in the design of most open channels.
The n value to be used for calculating the velocity in rock or boulder lined channels may be calculated by the following formulae:
- when 1.5 ≤ da/D50 ≤ 185.
- where:
- n = Manning’s roughness coefficient
- α = unit conversion constant, 0.262
- da = average flow depth in channel, ft
- D50 = mean stone size of the channel lining, ft
- when 0.3 ≤ da/D50 ≤ 1.5.
- where:
- n = Manning’s roughness coefficient
- α = unit conversion constant, 1.49
- da = average flow depth in channel, ft
- g = acceleration due to gravity, 32.2 ft/s2
- f(Fr) = Froude number
- f(REG) = roughness element geometry
- f(CG) = channel geometry
- where:
- T = channel top width, ft
- b = parameter describing the effective roughness concentration
The roughness coefficient of grassed channels varies depending on grass properties as reflected in the Cn parameter and the shear force exerted by the flow. This is because the applied shear on the grass stem causes the stem to bend, which reduces the stem height relative to the depth of flow and reducing the roughness. The following formulae may be used to estimate the n value for channels with grass linings, erosion control blankets or turf reinforcement mats.
- n =
- where:
- n = Manning’s roughness coefficient
- α = units correction constant, 0.213
- 𝜏o = mean boundary shear, lb/ft2
- Cn = roughness coefficient for SCS retardance class vegetation (see tables for Classification of Vegetal Covers and Coefficients for Roughness of Grass-Lined Channels)
- 𝜏o = γRSo
- γ = unit weight of water, 62.4 lb/ft3
- R = hydraulic radius, ft
- So = channel slope, ft/ft
SCS Retardance Class C vegetation is appropriate for most seed mixtures used on MoDOT roadway projects and Manning Formula for Grassed Channels provides a solution for the above equation for Class C Vegetation. As an alternative to the above equation, the values given in Roughness Coefficients for Various Materials for grass-lined channels may be used as a conservative estimate for hand calculations.
| Material | n Value |
|---|---|
| Concrete Culvert (pipe or box) | 0.013 |
| Corrugated Metal Pipe (CMP) | |
| 2-2/3 in. x 1/2 in. Corrugations | 0.024(1) |
| 3 in. x 1 in. Corrugations | 0.027 |
| 6 in. x 2 in. Corrugations (5 ft. diameter) | 0.033 |
| 6 in. x 2 in. Corrugations (7 ft. diameter) | 0.032 |
| 6 in. x 2 in. Corrugations (10 ft. diameter) | 0.030 |
| 6 in. x 2 in. Corrugations (15 ft. diameter) | 0.028 |
| Polyethylene Pipe | |
| Smooth | 0.012 |
| Corrugated | 0.024 |
| Concrete Paved Ditch | 0.015 |
| Grouted Riprap | 0.040 |
| Rock Ditch Liner Type 1 | 0.031 |
| Rock Ditch Liner Type 2 | 0.035 |
| Rock Ditch Liner Type 3 | 0.040 |
| Rock Ditch Liner Type 4 | 0.043 |
| Grass Lined Ditches (depth calculation) | 0.045 |
| Grass Lined Ditches (velocity/shear calculation) | 0.030 |
| Street Gutters and Pavements | 0.016 |
| (1) Manning's n for helically corrugated CMP may be less than above in certain conditions. See Appendix B of FHWA Hydraulic Design of Highway Culverts (HDS No. 5) for additional information. | |
| Retardance Class | Cover | Condition |
|---|---|---|
| A | Weeping lovegrass | Excellent stand, tall, average 30 in. |
| Yellow bluestem Ischaemum | Excellent stand, tall, average 36 in. | |
| B | Bermuda grass | Good stand, tall, average 12 in. |
| Native grass mixture (little bluestem, bluestem, blue gamma, and other long and short Midwest grasses | Good stand, unmowed | |
| Weeping lovegrass | Good stand, tall, average 24 in. | |
| Lespedeza serica | Good stand, not woody, tall, average 19 in. | |
| Alfalfa | Good stand uncut, average 11 in. | |
| Weeping lovegrass | Good stand, unmowed, average 13 in. | |
| Kudzu | Dense growth, uncut | |
| Blue gamma | Good stand, uncut, average 13 in. | |
| C | Crabgrass | Fair stand, uncut, avg. 10 in. |
| Bermuda grass | Good stand, mowed, average 6 in. | |
| Common lespedeza | Good stand, uncut, average 11 in. | |
| Grass-legume mixture - summer (orchard grass, redtop Italian ryegrass, and common lespedeza) |
Good stand, uncut, average 6 to 8 in. | |
| Centipedegrass | Very dense cover, average 6 in. | |
| Kentucky Bluegrass | Good stand, headed, 6 to 12 in. | |
| D | Bermuda grass | Good stand, cut to 2.5 in. height |
| Common lespedeza | Excellent stand, uncut, average 4.5 in. | |
| Buffalo Grass | Good stand, uncut, 3 t 6 in. | |
| Grass-legume mixture - fall (orchard grass, redtop Italian ryegrass, and common lespedeza) | Good stand, uncut, 3 to 5 in. | |
| Lespedeza serica | After cutting to 2 in. height, good stand before cutting | |
| E | Bermuda grass | Good stand, cut to average 1.5 in. height |
| Bermuda grass | Burned stubble | |
| Note: Covers classified have been tested in experimental channels. Covers were green and generally uniform. | ||
| Source: HEC-15 | ||
| SCS Retardance Class | Cn |
|---|---|
| Source: HEC-15 | |
Composite Roughness
Culverts using different materials for portions of the perimeter such as embedded culverts or culverts with an invert liner should use a composite Manning’s n value. A weighted n value based on the materials can be derived using the following equation:
- Where:
- nc = Composite/weighted Manning’s n.
- pi = Wetted perimeter for the material, ft.
- ni = Manning’s n value for the material.
- p = Total wetted perimeter, ft.
750.1.4.1.2 Hydraulic Radius
The hydraulic radius is a characteristic depth of flow and is defined as the cross-sectional area of flow divided by the wetted perimeter of the channel. The hydraulic radius is computed as follows:
- where:
- R = hydraulic radius, ft
- A = cross-sectional area of flow, ft2
- P = wetted perimeter of the channel cross section, ft
750.1.4.1.3 Slope
The slope to be used in the Manning Equation is the slope of the total energy or total head line. Under uniform flow conditions, the slope of the total energy line is equal to the slope of the channel bottom. Therefore, the channel bottom slope, expressed in ft/ft, is used for uniform flow design computations.
750.1.4.2 Uniform Flow Regimes
The regime of flow existing in a channel at any given time is a function of the channel geometry, channel slope, and discharge. The regimes of flow which may be present in an open channel are subcritical flow, critical flow and supercritical flow. The flow regime which exists under a given set of conditions may be determined by calculation of the Froude Number.
750.1.4.2.1 Froude Number
The Froude Number is defined as the ratio of the inertial forces (velocity) to the gravity forces, for a given set of flow conditions. The Froude Number is calculated as follows.
- where:
- F = Froude Number (unitless)
- V = mean velocity of flow, ft/s
- g = 32.2 ft/s2
- D = hydraulic depth, ft
The hydraulic depth is similar to the hydraulic radius in that both are characteristic depths of flow. However, they are defined differently. In open channel flow, the hydraulic depth, D, is defined as the cross-sectional area of flow, A, divided by the top width of the free surface, T, i.e. D = A/T, expressed in feet.
750.1.4.2.2 Subcritical Flow
Subcritical flow exists when the Froude Number is less than 1.0. Subcritical flow is sometimes referred to as tranquil flow and is characterized by low velocities and large depths. When a channel is operating in the subcritical flow regime, the formation of a hydraulic jump is not possible.
If the channel cross-section and the discharge are constant, then the regime of flow becomes a function of the slope of the channel. In this case, the slope of the channel defines the flow regime and the slope may be referred to as either subcritical slope (less than critical), critical slope, or supercritical slope (greater than critical). In order for subcritical flow to occur, the channel slope must also be subcritical.
750.1.4.2.3 Critical Flow
Critical flow will occur when the Froude Number is equal to 1.0. For a given channel cross section and discharge, critical flow will occur when the channel slope is equal to the critical slope.
Critical flow may also be defined as the flow condition at which, for a given channel section and discharge, the specific energy of the flowing water is at a minimum. The specific energy is defined as the depth of flow plus the velocity head and may be expressed as follows:
- where:
- E = the specific energy or specific head, ft
- d = depth of flow, ft
- V = mean velocity of flow, ft/s
- g = 32.2 ft/s2
The above definition of critical flow may be interpreted to mean that the energy required to convey a given discharge is at a minimum when the water is flowing in the critical regime.
The critical depth may be determined from the general expression for critical flow, which is given by:
- where:
- Q = discharge, ft3/s
- \alpha\ = velocity distribution coefficient
- g = 32.2 ft/s2
- Ac = cross-sectional area of flow at critical depth, ft
- Tc = top width of flow at critical depth, ft
750.1.4.2.4 Supercritical Flow
Supercritical flow will occur when the Froude Number is greater than 1.0. Supercritical flow is sometimes referred to as rapid or shooting flow and is characterized by high velocities and shallow depths. When a channel is operating in the supercritical regime, the formation of a hydraulic jump is possible. A hydraulic jump will occur when the flow regime changes from supercritical to subcritical in a short distance. For example, a hydraulic jump will occur in a channel if the channel slope abruptly changes from a supercritical value to a subcritical value.
750.1.4.3 Gradually Varied Flow
Truly uniform flow rarely exists in either natural or man-made channels. Changes in discharge, channel section, slope or roughness cause the depths and velocities to vary from point to point along the channel, and the water surface will not be parallel to the streambed. For many gradually varied non-uniform flow conditions, the flow is not too far from uniform and the assumption of uniform flow results in computed values that are close enough to the actual for all practical purposes. For this reason, the uniform flow assumption and Manning’s equation can generally be used to design artificial channels or to develop stage-discharge rating curves for determination of tailwater at a culvert or storm drain outlet. Under some conditions, however, the uniform flow assumption is not appropriate, and gradually varied water surface profile calculations must be made. The most commonly used method of computing water surface profiles is the step-backwater method, described below. Typical examples of non-uniform flow that may require calculation of water surface profiles include:
- A channel on a mild slope discharging into a pool. This situation often exists upstream of a bridge or culvert where, for instance, the headwater elevation required for flow through a culvert results in a pool upstream of the culvert that can influence water surface elevations for some distance upstream.
- A channel whose slope changes from subcritical (mild) to supercritical (steep). Flow passes through critical depth near the break in slope and uniform depth is not established for some distance downstream.
- Flow inside a culvert barrel when the barrel is not flowing full.
- A steep channel discharging into a mild channel or pool.
750.1.4.3.2 Step-Backwater Analysis
Step-backwater analysis is used for calculating water surface profiles for steady gradually varied flow conditions. Gradually varied water surface profiles are typically computed using the standard step method in which the stream reach of interest is divided into a number of subreaches by cross sections spaced so that the flow is gradually varied in each subreach. The energy equation is then solved in a step-wise fashion for the water surface elevation at one cross section based on the water surface elevation at the previous cross-section. Water surface profile computation therefore requires a beginning value of elevation or depth and proceeds upstream for subcritical flow and downstream for supercritical flow. In subcritical flow, uniform flow and normal depth at the most downstream cross section are ordinarily assumed as the boundary condition. In supercritical flow, critical depth is often the boundary condition at a control section.
The calculations involved in a step-backwater analysis are tedious and repetitive. It is recommended that a computer program such as the Corps of Engineers HEC-RAS be used for step-backwater calculations. See the documentation of the selected computer program for additional details on the step-backwater methodology used.
750.1.4.4 Manning's Equation for Circular Pipes
The Hydraulic Elements Graph will assist in the solution of Manning’s equation for part full uniform flow in circular pipes. The graph is presented in terms of ratios of hydraulic elements such as depth divided by diameter (d/D) and actual discharge divided by full flow discharge (Q/Qfull). When any one of the element ratios (d/D, Q/Qfull, V/Vfull) is known, the hydraulic elements graph can be used to determine any of the other ratios.
For circular pipes flowing full, Manning’s equation can be rearranged to provide the full flow discharge:
- where:
- K2 = constant = 0.46 English
- Qfull = discharge when pipe is flowing full, ft3/s
- n = a roughness coefficient
- D = pipe diameter, ft
- S = pipe slope, ft/ft
The full flow velocity (Vfull) can be determined using the continuity equation with the full flow discharge and cross-sectional area of the pipe.
750.1.5 Design of Non-Erodible Channels
Channels which are constructed from materials such as concrete and metal can withstand erosion under all but the most extreme conditions and are therefore considered non-erodible.
750.1.5.1 General Considerations
All non-erodible channels are to be designed on the basis of uniform open channel flow. The factors to be considered in design are the kind of material forming the channel lining; the "n" value of this material, the channel slope; the channel shape; and the freeboard. In addition to these hydraulic design factors, the designer must keep in mind other design limitations such as safety considerations. For example, the designer may be greatly restricted as to the channel shapes which may be considered inside a clear zone. In general, the object of design is to provide the least costly channel which has the required capacity and which will not scour. For non-erodible channels, this means selecting the smallest possible cross-section which will pass the design flow rate at the given channel slope. A factor of safety in channel design is introduced by addition of a freeboard to the computed depth of flow. For minimum freeboard to the top of the channel lining and to the top of the channel embankment, refer to EPG 748.3 Freeboard.
In order to reduce the number of computations required to design non-erodible channels, a set of open channel flow charts have been developed and are presented below. Depths and velocities shown by these charts apply with accuracy only to channels in which uniform flow at normal depth has been established. These charts may be applied with sufficient accuracy for practical purposes, to channels of somewhat irregular cross section approximating that represented by the chart and to channels on an irregular bottom slope where the irregularities are sufficiently short that they may be represented by a continuous mean slope.
750.1.5.2 Instructions for the Use of Trapezoidal Channel Charts
These charts are designed to enable direct solution of the Manning formula for uniform flow in trapezoidal channels with 2:1 side slopes, each chart applying to a fixed bottom width. The abscissa and ordinate scales represent discharge Q and normal velocity V for a roughness coefficient n = 0.030, when read in conjunction with the superimposed lines for slope So and normal depth of flow dn.
Depth of uniform flow for a given discharge in a given size of channel on a given slope and with a roughness coefficient n = 0.030 may be determined directly from the chart for that size by entering on the Q-scale and reading normal depth at the intersection with the appropriate slope line (or an interpolated slope.) Normal velocity may be read on the V-scale opposite this same point. This procedure may be reversed to determine discharge at a given depth of flow.
For channel roughness coefficients other than n = 0.030 compute the product Q times n and use the Qn and Vn scales. To obtain normal velocity V from the value on the Vn scale, divide the reading by n.
Critical depth dc for a given discharge is read by interpolation from the depth lines at the point where the Q-ordinate and the critical curve intersect, regardless of channel roughness. Critical velocity Vc is the reading on the V-scale for this same point.
750.1.5.3 Instructions for Use of Trapezoidal and Triangular Channel Charts
8 ft. Channel Chart - 6:1, 2:1
8 ft. Channel Chart - 6:1, 3:1
V-Bottom Channel Chart - 3:1, 2:1
V-Bottom Channel Chart - 4:1, 2:1
V-Bottom Channel Chart - 4:1, 3:1
V-Bottom Channel Chart - 4:1, 4:1
V-Bottom Channel Chart - 6:1, 2:1
V-Bottom Channel Chart - 6:1, 3:1
These charts were developed to enable direct solution of the Manning formula for the two trapezoidal sections most often used inside safety zones and for various triangular sections. These charts apply only to the cross section shown on the figures and are used in a manner similar to the charts for trapezoidal cross-sections with 2:1 side slopes as previously discussed.
Depth of flow for a given discharge in a given channel on a given slope and with a roughness coefficient n = 0.030 may be determined directly from the chart for that channel by entering on the Q-scale and reading normal depth at the intersection with the appropriate slope line (or an interpolated slope.) Normal velocity may be read on the V-scale opposite this same point. This procedure may be reversed to determine discharge at a given depth of flow.
For channel roughness coefficients other than n = 0.030 compute the product Q times n and use the Qn and Vn scales. To obtain normal velocity V from the value on the Vn scale, divide the reading by n.
Critical depth dc for a given discharge is read by interpolation from the depth lines at the point where the Q-ordinate and the critical curve intersect, regardless of channel roughness. Critical velocity Vc is the reading on the V-scale for this same point.
750.1.5.4 Instructions for Use of Pipe Flow Charts
Pipe Flow Chart - 12 Inch Diameter
Pipe Flow Chart - 15 Inch Diameter
Pipe Flow Chart - 18 Inch Diameter
Pipe Flow Chart - 21 Inch Diameter
Pipe Flow Chart - 24 Inch Diameter
Pipe Flow Chart - 30 Inch Diameter
Pipe Flow Chart - 36 Inch Diameter
Pipe Flow Chart - 42 Inch Diameter
Pipe Flow Chart - 48 Inch Diameter
Pipe Flow Chart - 54 Inch Diameter
Pipe Flow Chart - 60 Inch Diameter
Pipe Flow Chart - 66 Inch Diameter
Pipe Flow Chart - 72 Inch Diameter
Pipe Flow Chart - 84 Inch Diameter
These charts are designed to enable direct solution of the Manning equation for flow in circular pipes. Each chart applies to a certain diameter pipe.
Depth of uniform flow for a given discharge Q in a given size pipe on a given slope So, and with roughness coefficients n = 0.013, 0.015, or 0.024 may be determined directly from the chart for that size by entering on the appropriate slope line (or an interpolated slope). Normal velocity may be read on the appropriate V-scale opposite this same point. The procedure may be reversed to determine discharge at a given depth of flow.
Where the Q-ordinate intersects a slope line, So, in the area near its right terminus, two alternate depths will be indicated if dn is greater than 0.82 diameters. For these cases, flow will occur at the lesser of the alternate depths.
For pipe roughness coefficients other than those of n = 0.013, 0.015 or 0.024 shown on the chart scales, enter the chart on the inner scale for n = 0.015 with an adjusted value of Q = Q design x n/0.015 to determine depth and velocity. Read depth directly from the chart at the pipe slope line, So, and obtain the velocity by dividing the value read on the V-scale for n = 0.015 by the ratio n/0.015. In reversing the above procedure to determine Q for a given depth, read Q on the scale for n = 0.015 and divide by the ratio n/0.015 to obtain the flow rate, Q.
The maximum rate of discharge of any circular pipe on a given slope, not flowing under pressure, will occur with a depth of flow of 0.94 diameters. Therefore, to determine the maximum open channel capacity of a pipe on a given slope, read the Q-ordinate for the appropriate value of n at the maximum value reached by the sharply curved slope line (depth equals 0.94 diameters).
750.1.5.5 Instructions for Use of Rectangular Channel Charts
4 ft. Channel Chart - Vertical
5 ft. Channel Chart - Vertical
6 ft. Channel Chart - Vertical
7 ft. Channel Chart - Vertical
8 ft. Channel Chart - Vertical
9 ft. Channel Chart - Vertical
10 ft. Channel Chart - Vertical
12 ft. Channel Chart - Vertical
14 ft. Channel Chart - Vertical
These charts are designed to enable direct solution of the Manning equation for uniform flow in rectangular channels, each chart applying to a fixed bottom width.
Depth of uniform flow for a given discharge in a given size of channel on a given slope and with a roughness coefficient n = 0.015 may be determined directly from the chart for that size by entering on the Q-scale and reading normal depth at the intersection with the appropriate slope line (or an interpolated slope). Normal velocity may be read on the V-scale opposite this same point. This procedure may be reversed to determine discharge at a given depth of flow.
For channel roughness coefficients other than n = 0.015 compute the product Q times n and use the Qn and Vn scales. To obtain normal velocity from the value on Vn scale, divide the reading by n.
Critical depth dc for a given discharge is read by interpolation from the depth lines at the point where the Q-ordinate and the critical curve intersect, regardless of channel roughness. Critical velocity Vc is the reading on the V-scale for this same point.
Where n = 0.015 critical slope Sc is read at the critical depth point as found above. Critical slope will vary with channel roughness, therefore, to determine critical slope for other values of roughness coefficient it is first necessary to determine critical depth. Critical slope is then interpolated from the slope lines at the intersection of this depth with the Qn ordinate.
750.1.6 Design of Channels with Flexible Linings
Flexible linings are those able to conform to changes in channel shape and include grass, rock and synthetic linings. Advantages of flexible linings over rigid linings are that they are generally less expensive than non-erodible linings, permit infiltration of water and provide a more natural appearance. Flexible linings are also able to adapt to minor changes in channel shape, while rigid linings are not. Rigid linings are prone to failure when some portion of the lining is damaged.
Flow of water in a channel with flexible linings may be analyzed by the Manning formula. However, the solution to the problem is complicated because a single n value cannot be used to describe the retardance in such channels. The n value for a given flexible lining is generally a function of the channel slope and the hydraulic radius of the channel cross-section.
The general procedure for design of channels with grass linings involves an iterative process, since flow depth depends on roughness and roughness depends on flow depth. The steps required to determine an appropriate roughness coefficient and flow depth are as follows:
1) An arbitrary roughness coefficient (nest) is assumed and used with the ditch geometry and discharge to determine a calculated flow depth (dcalc).
2) This calculated flow depth (dcalc) is next used to determine the corresponding roughness coefficient (ncalc) from Mannning's Roughness for Retardance Class C Vegetation.
3) If the two roughness coefficients, nest and ncalc, are within an acceptable tolerance, the calculated flow depth and roughness coefficient are considered correct; otherwise, the procedure is repeated, using the calculated roughness coefficient as a new estimate (nest) to determine a new calculated flow depth (dcalc).
Design of channels with flexible linings is based on the criterion of maximum permissible tractive force or shear stress. Procedures for determination of shear stress at a channel lining are given in Erosion Control and Energy Dissipation. The shear stress can then be calculated and compared to the maximum permissible shear stress for the chosen lining type. If the shear stress is greater than permissible, the lining type is not acceptable, and another lining must be chosen.
For more information, refer to FHWA publication HEC-15 Design of Roadside Channels with Flexible Linings.





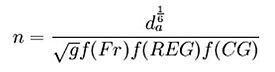





![{\displaystyle n_{c}={\Bigg [}{\frac {\Sigma (p_{i}n_{i}^{1.5})}{p}}{\Bigg ]}^{0.67}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6662bedc0366bfe88396948f02080e56549b7376)




