Difference between revisions of "321.1 Design of Earth Slopes"
| Line 162: | Line 162: | ||
|Despite the fact that stability is really a strength limit state, load factors associated with the Service I limit state are used for all loads by convention with current AASHTO LRFD procedures. This position makes some sense when considering earth loads that often have little variability and uncertainty, but may not make sense when stability is dominated by loading from bridge or other structures. | |Despite the fact that stability is really a strength limit state, load factors associated with the Service I limit state are used for all loads by convention with current AASHTO LRFD procedures. This position makes some sense when considering earth loads that often have little variability and uncertainty, but may not make sense when stability is dominated by loading from bridge or other structures. | ||
|} | |} | ||
| − | Loads to be used for stability evaluations shall be factored according to the Service I limit state. Accordingly, a load factor of 1.0 shall be used for all applied loads, including “surcharge” loads associated with foundations or other surface loads. The soil unit weight shall also be factored using a<div id=" | + | Loads to be used for stability evaluations shall be factored according to the Service I limit state. Accordingly, a load factor of 1.0 shall be used for all applied loads, including “surcharge” loads associated with foundations or other surface loads. The soil unit weight shall also be factored using a load factor of 1.0. |
| + | <div id="321.1.2.4 Resistance factors"></div> | ||
===321.1.2.4 Resistance factors for short-term, undrained conditions=== | ===321.1.2.4 Resistance factors for short-term, undrained conditions=== | ||
Revision as of 14:51, 5 September 2013
| Commentary Boxes |
| These boxes will provide supplemental information or commentary on application of specific provisions, supporting documentation for the provisions, or explanations for how the provisions should be applied. |
This article provides requirements for design of earth slopes commonly encountered in transportation rights of way. Such slopes commonly include embankment slopes for fills and bridge approaches and excavated slopes in cut sections of roadway. Earth slopes should be designed to maintain stability for conditions and loads that can reasonably be expected to be encountered throughout the life of the slope based on available information regarding site conditions and anticipated loadings. Earth slopes should also be designed such that excessive deformations are not experienced throughout the life of the structure or so that deformations that do occur do not adversely affect the travel way.
In the context of these guidelines, “design” of earth slopes generally involves selection of some combination of the following to produce a final slope that will satisfy performance requirements:
- 1) Slope geometry to include slope inclination, slope width, and slope height,
- 2) Slope materials to include selection of fill materials for embankments,
- 3) Materials and methods to provide for appropriate drainage of surface and/or groundwater,
- 4) Materials and methods for reinforcing a slope to provide necessary stability, and
- 5) Loading conditions
For any given slope, some of these parameters will be constrained to satisfy site or project specific requirements so the specific parameters that can be varied to produce acceptable performance will be case dependent.
| The provisions of EPG 321.1.2 and EPG 321.1.3 shall be followed for site/location specific stability analyses and for overall stability evaluations for retaining walls and spread footings. |
The remainder of these guidelines is organized into three different sections. EPG 321.1.1 describes general requirements and limits for earth slopes that can be considered routine. The majority of slope designs will be established based on the provisions in this section. EPG 321.1.2 describes provisions that apply for special slope stability problems to include design of remedial measures for sites where slides have occurred, evaluation and design of relatively large embankments on soft soils, and other complex slope stability problems that generally involve considerable risk and potential expense.
Contents
321.1.1 Slope Inclination for Preliminary Geotechnical Report
The majority of soil and rock slopes designed for transportation right of way will be designed based on the provisions of this section. Complex slope stability cases (e.g. cases where there is uncertainty regarding likely loading or ground conditions), cases where the consequences of failure are great (e.g. slopes supporting foundations for bridges or retaining walls, unusually large fills, etc.), or cases where a slide has already occurred shall be designed according to EPG 321.1.2 and EPG 321.1.3.
321.1.1.1 Soil Slopes
For design of routine slopes without notable complications, the guidelines provided in Table 321.1 shall be used to select an appropriate maximum slope inclination based on the soil/rock types present at the specific site. These recommendations should be considered along with other factors that may influence the stability and performance of slopes in establishing final design recommendations. Factors such as presence or absence of structural foundations, adverse seepage conditions, susceptibility to inundation, or presence of notably poor soil/rock, etc. may dictate use of flatter slopes. MCHRP Report 79-1 provides recommendations for handling of notoriously problematic soils including gley, Cheltenham claystone, and Maquoketa clay shale. Soils classified as OH, OL and MH in the ASTM classification are rare and, if encountered, will require special design and/or handling.
Table 321.1 Guide for Selection of Slope Inclination for Routine Design
| Geologic Origin | Glacial, Alluvial and Loessial Soils (Rock-free Residual Soils Derived from Shale, Claystone and Siltstone) | Residual Soil with Admixed Chert or Rock Fragments 4 | Class C 5 | ||||
|---|---|---|---|---|---|---|---|
| General Description | Sand1 | Silt/Loess2 | Clay of Low Plasticity | Clay of High Plasticity3 | |||
| ASTM Classification | SP,SM | SW,SC | ML, ML-CL | CL | CH | CL,CH,GC | |
| Backslope | 1V:2.5H (2.5:1) | 1V:2.0H (2.0:1) | 1V:2.5H (2.5:1) | 1V:2.5H (2.5:1) | 1V:3.0H (3.0:1) | 1V:2.0H (2.0:1) | (Standard) |
| Fill Side Slope | 1V:2.5H (2.5:1) | 1V:2.0H (2.0:1) | 1V:2.5H (2.5:1) | 1V:2.5H (2.5:1) | 1V:3.0H (3.0:1) | 1V:2.0H (2.0:1) | 1V:2.0H (2.0:1) |
| Fill Spill Slope6: | |||||||
| H ≤ 20 ft. | 1V:2.5H (2.5:1) | 1V:2.0H (2.0:1) | 1V:2.0H (2.0:1) | 1V:2.0H (2.0:1) | 1V:2.5H (2.5:1) | 1V:2.0H (2.0:1) | 1V:2.0H (2.0:1) |
| H > 20 ft. | 1V:2.5H (2.5:1) | 1V:2.0H (2.0:1) | 1V:2.5H (2.5:1) | 1V:2.5H (2.5:1) | 1V:3.0H (3.0:1) | 1V:2.0H (2.0:1) | 1V:2.0H (2.0:1) |
| 1 Soil caps to control erosion may be required for sandy soils other than SC soils. | |||||||
| 2 Essentially vertical cut slopes may be used in loess when indicated to be practical by criteria outlined in MCHRP Report 74-1 | |||||||
| 3 Soils with extremely high PI (>50) should be used with extreme caution. Consideration should be given to wasting such materials or to use of even flatter slopes than those listed. | |||||||
| 4 Consider flatter slopes where height of fill exceeds 40 feet and percentage of admixed granular material is less than 40 percent. Refer to MCHRP Report 75-1 for additional information. | |||||||
| 5 Locally steeper slopes for Class C fills are practical only with special handling in excavation and placement. | |||||||
| 6 Steeper slopes for low spill slopes assume that some form of slope protection be used to control erosion and/or seasonal moisture changes. | |||||||
In most cases, a single value for slope inclination shall be selected for an entire project. See commentary for additional explanation and description.
Slope inclinations for excavated (cut) slopes shall be based on Table 321.1 and are to be carried uninterrupted beneath structures regardless of the height of cut. No steepening or warping of cut slopes shall be allowed, including cut slopes less than 20 ft. high.
321.1.1.2 Rock Slopes
Rock slopes in limestones, dolomites and sandstones are normally cut vertically or with a slight batter. Benches shall be provided at a vertical spacing not to exceed 30 ft. for cut slopes greater than 30 ft. high. Benches shall be a minimum of 10 ft. wide. Benches may be provided at the contacts of different formations (not necessarily at 30 ft.) and may vary in width.
Cut slopes in shale, siltstone, and other soft rocks shall be inclined at 1V:2H (2:1).
A flat bottom ditch with a minimum width of 10 ft. is required for all rock cut slopes.
| Commentary on EPG 321.1 Slope Inclination for Preliminary Geotechnical Report |
| It is not intended that a slope’s inclination be varied with different soil horizons or for each soil type encountered. Rather, the slope inclination selected for a project shall be determined from an overall evaluation of the predominant soils encountered on a project. In the event of uncertainty, a conservative selection of inclination should be made, or site specific analyses according to EPG 321.1.2 shall be required. For example, A and B horizons will normally be relatively thin and less plastic compared to the C horizon. In such cases, the slope selection would logically be based on the C horizon as both the worst and predominant material to be encountered. |
| In most cases, a constant slope inclination shall be used throughout a given project. Slope inclinations should only be varied horizontally within a project if the alignment traverses two or more distinct soil types and only if it is known where material from any cut in the transition zone will be placed in fill. In the event of uncertainty, the more conservative slope should be extended to the point where the uncertainty is minimal. |
| A somewhat common source of confusion with Table 321.1 has been in selecting slopes for some CH residual soils. Note that the top column of the chart deals with geologic origin and this is the first division before looking at ASTM classification. A CH soil residual from rock with admixed chert or other rock fragments may be constructed with an inclination of 1V:2H (2:1). However, a slope inclination of 1V:3H (3:1) is required for a CH residual soil derived from shale and claystone - and without admixed granular material. |
| A soil series that has been especially confusing is the Union. The lower part of the profile is typically a cherty, residual clay and the upper part is of wind-blow origin, usually CL. Soil survey recommendations have ranged from 1V:2H (2:1) through 1V:3H (3:1). The 1V:3H (3:1) has been based on the CH classification, which is a misinterpretation since it is a CH residual from carbonates and is cherty. The slope selected should be based on the predominant phase. If it is mostly CL loess with only a few feet of residual soil, the 1V:2.5H (2.5:1) should probably be used. If it is almost all residual soil with only a few feet of windblown soil then 1V:2H (2:1) should be adequate. |
| It should be emphasized that this chart is a guide. It is based on some theory and it is tempered by experience. It fits most situations, but there are exceptions. Some of the exceptions have been addressed in research reports. For the most part, this chart is based on stability considerations, but in one area it is been shaded a bit for erosion control purposes. This is for the ML loesses. When dealing with a very tight right of way situation, it may be practical to steepen slopes in this material to 1V:2H (2:1) at the expense of some increased erosion problems or erosion control measures. If in doubt, shear tests can be done. To repeat, this chart is a guide - it is not carved in stone. |
| For grade separations, consideration should be given to selective grading of fill materials such that better materials are placed in fill spill slopes (i.e. beneath bridge abutments) so that the spill slopes can be steepened. While such handling will likely increase costs for fill placement, some additional handling can be justified if it results in reducing bridge length. Selective fill placement is not generally practical on stream crossings -- only on grade separations. |
| Table 321.1 permits spill slopes to be 1V:0.5H (0.5:1) steeper than side slopes for several soil types, but no steeper than 1V:2H (2:1), where the elevation differential between the toe of slope and grade at the bridge end is less than 20 feet. This recognizes the fact that the effective height of the spill slope will be reduced by at least 6 to 8 ft. because of the abutment headwall. This concept becomes more complicated at stream channel crossings where it is necessary to consider the depth and condition of the stream channel and their effect on bridge end location. For example, one might have CL glacial soils and a height differential between grade and toe of slope of some 15 feet. Table 321.1 requries 1V:2.5H (2.5:1) side slopes and 1V:2H (2:1) spill slopes for CL fill soils. However, if the stream channel is entrenched in CL soil another 15 feet deep such that the total height differential is greater than 20 feet, the bridge ends should be stepped back to or beyond a point determined by projecting a 1V:2.5H (2.5:1) upward from the toe of the channel slope to intersection with grade. For typically steep channel banks, this will generally leave a substantial bench at natural ground level, which provides some room for bank sloughing without affecting the integrity of the spill slope. The spill slope would remain at 1V:2H (2:1) but the bridge end would be located as if it were at least 1V:2.5H (2.5:1). |
| Now things get even more complicated. To this point, we have not really considered some of the possible complications to the stability of stream and channel slopes. There is a caution in the text beneath the slope selection chart that, "Factors such as foundations, seepage, susceptibility to inundation, etc. may dictate flatter slopes." Even ignoring foundations, which call for a special investigation, there is no simple way of considering the effects of water that will fit every case. Determining proper slopes in such circumstances involves consideration of a complex intermingling of factors such as flooding rate, height and duration, rate of recession, water velocity, scour potential, soil strength, weight, permeability, swell potential, and seepage rates, all further complicated by considerations of costs and the risks and consequences of failure. |
| The following general comments and guidelines are offered, however, to supplement the Guide for Slope Recommendations. First, use the chart to determine the slope (spill or side) you would use if water were not a factor. This is the slope to which you will make adjustments based on the following considerations. |
| For moderate stream flows of average flood duration, about 1V:0.5H (0.5:1) flatter may suffice. For prolonged flooding followed by drawdown, 1:1 flatter may be appropriate. For intermittent or low-flow streams subject only to flash flooding, no flattening may be needed. Always inspect stream slopes for evidence of slides and sloughs and inspect the condition of adjacent structures over the same stream. Consider the width of the embankment; a 4-lane roadway is more likely to fail into a stream channel than a narrow county road or railroad fill. Consider also the consequences of failure; be more conservative for heavily traveled arterial roadways than for minor or rural supplemental roads for example. |
| Keep in mind that many stream channel slopes are stable only because of mature tree growth along the banks and the reinforcement provided the banks by the root structure. Remember that trees will be destroyed by construction, the roots will rot, and maintenance will prevent their regrowth. The net result will be less inherent stability where most needed. |
| Channelization has led to much stream bank instability, particularly in the northwest part of the state. It is especially prevalent in Lafayette, Atchison and Holt Counties. The invariable result is channel deepening, sometimes severe deepening. Careful examination of banks will often reveal massive slides, sometimes so massive as to resemble natural terraces. Always look at your county map; if the stream follows a straight line, it has been channelized. The streambed will have deepened and the banks, if not already failed, will be in precarious condition. |
321.1.2 Slope Stability Analyses for Special Foundation Investigations
The provisions of this article shall be used for design and analysis of slopes for non-routine slope design. The most common instances for these “site specific” designs is for cases where slides have already occurred, cases with complex site and/or loading conditions, and cases with substantial consequences of failure (e.g. high fills, embankments of soft foundation soils, and slopes with bridge foundations). The provisions of this section shall also be followed for evaluation of overall stability for retaining walls and spread footings founded within slopes.
321.1.2.1 General Considerations
Embankment (fill) and excavated (cut) slopes shall be designed to remain stable throughout the anticipated life of the slope without excessive deformations. The provisions of this article address the issue of stability, or the strength limit state.
321.1.2.2 General Procedure for Slope Stability Analysis Using LRFD Approach
| The procedure for design of earth slopes following LRFD is quite similar to procedures for conventional ASD analysis, with two important differences. The first difference occurs in No. 4, where factored parameters are used as input for the slope stability analyses for LRFD analyses whereas unfactored parameters are used for the traditional ASD analyses. The second difference occurs in No. 5, where instead of comparing the computed factor of safety to some required or target factor of safety as is done in ASD, the computed factor of safety is compared to a limit value (= 1.0) indicating stability or instability. In this respect, the LRFD procedure is indeed more straightforward than current procedures in that the analysis target or limit is consistent for all stability cases for the LRFD procedure whereas the analysis target for conventional ASD procedures varies from one application to another. The result of these differences is simply that, for LRFD procedures, uncertainties in the analyses are accounted for through factoring of the input parameters whereas for ASD procedures the uncertainty is accounted for through a single factor of safety. By factoring individual input parameters, it is possible to more appropriately apply conservatism to the individual parameters involved in the analysis, and therefore to effect more consistent levels of safety across a broad range of cases. Both load and resistance factors in LRFD and factors of safety in ASD are intended to account for uncertainties involved in the respective analyses. They are simply different methods for accounting for these uncertainties. |
| Five common parameters are used for slope stability analyses including the soil (total) unit weight, , undrained shear strength, su, Mohr-Coulomb shear strength parameters, c and (or and in the case of effective stress analyses), and the pore water pressure, u. For the current implementation, neither soil unit weight nor pore water pressures are factored. Soil unit weight is not factored because it generally contributes little towards the reliability of an earth slope so that appropriate values for the load factor would only be slightly greater than 1.0 (generally less than 1.03). The variability and uncertainty in the unit weight is thus accounted for in the resistance factors for soil shear strength. In contrast, pore water pressures, and the variability/uncertainty in pore pressure, has a dramatic influence on the reliability of a given slope. Unfortunately procedures for rationally estimating and factoring pore pressures for LRFD analyses have not yet been established so procedures for handling pore water pressures, or piezometric lines and other constructs used to model pore water pressures, remain unchanged and should be estimated following procedures identical to those used for traditional ASD procedures. |
Design of earth slopes according to LRFD concepts can be confusing because current methods for stability analysis commonly produce a “factor of safety”, which is an artifact of traditional ASD methods. While potentially confusing, this fact does not preclude use of LRFD for design of earth slopes, but it does necessitate slight changes to current procedures used for analysis and design of earth slopes (Loehr et al., 2006).
The following procedure shall be utilized for design of earth slopes according to these provisions:
- 1) Establish site geometry and stratigraphy using available geologic information, boring logs, site surveys and plans, and other information available to the designer;
- 2) Estimate parameters for each respective stratum within the slope using available laboratory test results, empirical correlations, back-calculations, and other available information;
- 3) Estimate anticipated pore pressure conditions (required only for effective stress analyses) based on available historical records and judgment;
- 4) Evaluate the factor of safety for the conditions established using appropriate slope stability analysis methods with factored parameters as input; and
- 5) Compare the computed factor of safety to the limit factor of safety (= 1.0):
- a) If the computed factor of safety is approximately equal to 1.0, the design is considered acceptable.
- b) If the factor of safety is significantly greater than 1.0, changes to reduce the computed factor of safety may be considered if significant cost savings can be realized.
- c) If the factor of safety is less than 1.0, the designer must consider alternative measures to increase the factor of safety and repeat the procedure until a factor of safety approximately equal to 1.0 is achieved.
Current procedures will factor the undrained shear strength, su, or the Mohr-Coulomb shear strength parameters, c and ϕ (or and ). Resistance factors for factoring of these parameters are provided in EPG 321.1.2.4.
321.1.2.3 Load Factors
| Despite the fact that stability is really a strength limit state, load factors associated with the Service I limit state are used for all loads by convention with current AASHTO LRFD procedures. This position makes some sense when considering earth loads that often have little variability and uncertainty, but may not make sense when stability is dominated by loading from bridge or other structures. |
Loads to be used for stability evaluations shall be factored according to the Service I limit state. Accordingly, a load factor of 1.0 shall be used for all applied loads, including “surcharge” loads associated with foundations or other surface loads. The soil unit weight shall also be factored using a load factor of 1.0.
321.1.2.4 Resistance factors for short-term, undrained conditions
| Resistance factors for short-term stability analyses were calibrated probabilistically to produce a target probability of failure of approximately 1 in 2000. This target probability of failure reflects the fact that most short-term stability failures are relatively deep and massive (and thus costly) so that a relatively low target probability of failure is desired. |
Stability analyses for short-term, undrained conditions (generally associated with conditions during or shortly after construction) should be performed using factored shear strength parameters established in terms of total stresses without consideration of pore water pressures (i.e. total stress analyses). In general, the resistance factor to be used is dependent on the slope stability parameter, λcϕ, which is determined as
| (dimensionless) | Equation 321.1.2.4.1 |
where is the total unit weight for the soil, H is the slope height, and c and tanϕ are respectively the intercept and slope of the Mohr-Coulomb failure envelope for the soil in question.
For conditions and strata that can be considered as ϕ = 0 conditions (saturated soil, undrained loading), the undrained shear strength(s) should be factored as
| (consistent units of stress) | Equation 321.1.2.4.2 |
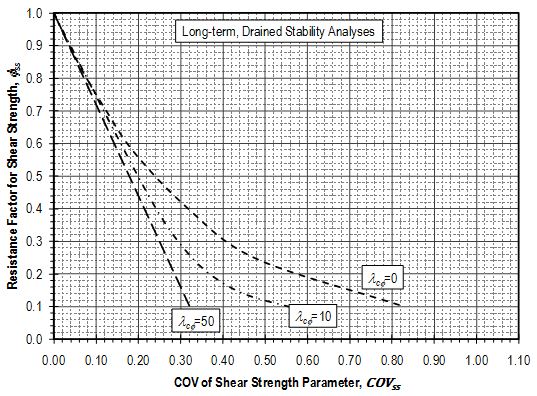
where is the factored undrained shear strength, su is the nominal value of shear strength, and ϕss is the resistance factor determined from Fig. 321.1.2.4 for λcϕ = 0. For conditions that can be represented by Mohr-Coulomb shear strength parameters c and ϕ, in terms of total stresses, the Mohr-Coulomb shear strength parameters should be factored as
| (consistent units of stress) | Equation 321.1.2.4.3 | |
| (dimensionless) | Equation 321.1.2.4.4 |
where and tanϕ* are respectively the factored intercept and slope of the Mohr-Coulomb failure envelope, c and tanϕ are respectively the nominal intercept and slope of the Mohr-Coulomb failure envelope, and ϕss is the resistance factor determined from Figure 321.1.2.4 for the appropriate value of λcϕ and COV of Shear Strength Parameter, COVss, as determined in accordance with EPG 321.3. Note that it is the tangent of the friction angle that is factored rather than the friction angle itself.
321.1.2.5 Resistance factors for long-term, fully drained conditions
| Resistance factors for long-term stability analyses were calibrated probabilistically to produce a target probability of failure of approximately 1 in 400. This target probability of failure reflects the fact that most long-term stability failures are relatively shallow (and thus less costly) so that a relatively greater target probability of failure is desired. |
Stability analyses for long-term, drained conditions (generally associated with conditions long after construction) should be performed using factored shear strength parameters in terms of effective stresses (i.e. effective stress analyses). In general, the resistance factor to be used is dependent on the slope stability parameter, λcϕ, which is determined as
| (dimensionless) | Equation 321.1.2.5.1 |
where is the total unit weight for the soil, H is the slope height, and and are respectively the intercept and slope of the Mohr-Coulomb failure envelope for the soil in terms of effective stresses.
The Mohr-Coulomb shear strength parameters established in terms of effective stresses should be factored as
| (consistent units of stress) | Equation 321.1.2.5.2 | |
| (dimensionless) | Equation 321.1.2.5.3 |
where and are respectively the factored intercept and slope of the Mohr-Coulomb failure envelope, and are respectively the nominal intercept and slope of the Mohr-Coulomb failure envelope established in terms of effective stresses, and ϕss is the resistance factor determined from Figure 321.1.2.5 for the appropriate value of λcϕ and COV of Shear Strength Parameter, COVss, as determined in accordance with EPG 321.3. Note that it is the tangent of the friction angle that is factored rather than the friction angle itself.
Pore pressure conditions, which may be represented in a number of different ways for stability analyses (e.g. piezometric lines, pore pressure ratio, etc.), should be selected using all available information as well as sound judgment, just as it would be following traditional ASD analysis methods. It is important that the pore pressure conditions used reflect the worst-case pore pressure conditions anticipated over the life of the slope.
321.1.3 Serviceability
| Serviceability of other slopes, and lateral deformations are controlled by use of appropriate conservatism in the resistance factors from EPG 321.1.2. The serviceability check for settlement of embankments is primarily intended for use as a criterion for deciding whether bridge approach slabs are necessary and justified, and potentially for establishing when settlement has occurred to a sufficient extent to complete construction in cases where staged construction is planned, or when final paving of a project is being postponed until embankment settlements will be less than established tolerable limits. |
The serviceability limit state requirements of this section are intended to provide for evaluation of the potential for excessive settlement of embankments. The primary application of this section is expected to be for predicting settlement of bridge approach embankments to establish whether bridge approach slabs are justified. The provisions of this section may also be utilized to establish whether the remaining settlement of an embankment is sufficiently low to proceed with final paving for projects where final paving is postponed to allow embankment settlement to occur.
321.1.3.1 General Considerations
In general, settlement at the surface of an embankment can arise from compression of the foundations soil due to the weight of the overlying embankment fill soils and compression of the embankment fill soils (e.g. due to wetting induced compression, etc.). This section includes provisions for prediction of settlement from both sources. Factored settlements are determined using factor consolidation parameters to reflect the uncertainty and variability present at the specific site in question. The total factored settlement is computed as the sum of the factored compression of the foundation soils and the factored compression of the embankment
| (consistent units of stress) | Equation 321.1.3.1 |
Where is the total factored settlement, is the factored compression of the foundation soils due to the weight of the overlying fill, and is the factored compression of the embankment soils. Provisions for estimation of and are provided below.
321.1.3.2 Settlement Due to Compression of Foundation Soils
| The factored compression of the foundation soil is computed in a manner very similar to that use for estimating the factored settlement of spread footings on soil. However, the resistance factors that are used for estimating these two settlements are different. The differences arise from the fact that the change in stress due to loading from a spread footing is more uncertain and variable than is loading from embankment soils. The resistance factors presented reflect this difference. |
The factored settlement for embankments on cohesive soils shall be computed following classical consolidation theory (e.g. Reese et al., 2006), modified to include resistance factors to be applied to the compression and recompression indices, cc and cr, and to the maximum past vertical effective stress, σ'p (also referred to as the pre-consolidation stress). Application of this method within the LRFD framework requires comparison of a factored value for σ'p, with the initial and final vertical effective stresses, σ'o and σ'f, within the foundation soils.
If σ'o < ϕp σ'p < σ'f, the factored total settlement shall be computed as:
| (consistent units of length) | Equation 321.1.3.2.1 |
Where:
- σ'0 = vertical effective stress (consistent units of stress),
- ϕp = resistance factor to be applied to pre-consolidation stress (dimensionless),
- σ'p = maximum past vertical effective stress (consistent units of stress),
- σ'f = final vertical effective stress (consistent units of stress),
- δR = factored settlement (consistent units of length),
- H0 = thickness of compressible layer (consistent units of length),
- e0 = initial void ratio (dimensionless),
- cc = compression index (dimensionless),
- ϕc = resistance factor to be applied to compression index term (dimensionless),
- cr = recompression index (dimensionless), and
- ϕr = resistance factor to be applied to recompression index term (dimensionless).
If ϕpσ'p ≥ σ'f, the factored settlement shall be computed as:
| (consistent units of length) | Equation 321.1.3.2.2 |
Similarly, if ϕpσ'p ≤ σ'f, the factored settlement shall be computed as:
| (consistent units of length) | Equation 321.1.3.2.3 |
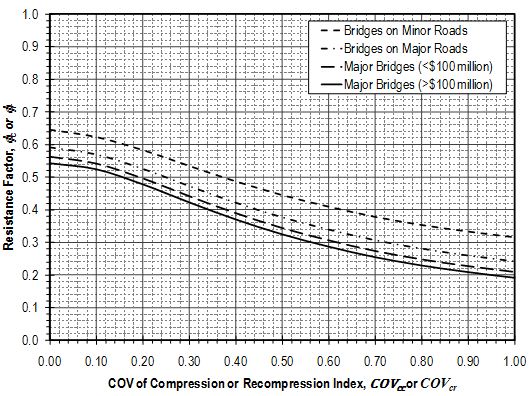
Values for ϕc and ϕr shall be established from Figure 321.1.3.2.1 based on the coefficient of variation of the mean compression index and mean recompression index , respectively. Similarly, values for ϕp shall be established from EPG 321.1.3.2 based on the coefficient of variation of the mean maximum past vertical effective stress . Coefficients of variation for each of these parameters shall be determined in accordance with methods described in EPG 321.
Where embankments are underlain by compressible soils of substantial thickness, the soil beneath the embankment shall be subdivided into several sublayers to account for potential changes in consolidation parameters and stress distribution beneath the embankment. Compression of each of these sublayers shall be computed using Equation 321.1.3.2.1, 321.1.3.2.2 or 321.1.3.2.3, as appropriate, and the resulting values should be summed to arrive at the total settlement. For each sublayer, values for cc, cr, and e0 shall be taken as the mean values of these parameters over the thickness of the sublayer. Values for H0 shall be taken as the thickness of the respective sublayer. Values for σ'0, σ'f and σ'p for each sublayer shall also be taken as the mean values over each sublayer, although this is often approximated by using values calculated for the center of the sublayer. Values used for , and shall be representative of the variability and uncertainty of the mean values for the respective parameters within each sublayer.
Where conditions warrant, settlement contributions due secondary compression shall be added to those computed from Equations 321.1.3.2.1, 321.1.3.2.2 or 321.1.3.2.3.
321.1.3.3 Settlement Due to Compression of Fill
The factored compression of the embankment soils shall be computed as
| (consistent units of length) | Equation 321.1.3.3 |
Where Hfill is the total fill thickness and ϕfill is the resistance factor for embankment compression. The value of ϕfill shall be taken as 0.62.
| Commentary on EPG 321.1.3.3 |
| The estimate provided is based on observational data suggesting that the compression of embankments constructed following common compaction specifications is between 1 and 3 percent of the embankment height. |
| The resistance factor for compression of the embankment soils will produce a value of settlement that has an approximately 1 in 150 chance of settlements exceeding that value. |
321.1.3.4 Settlement Limits
For deciding whether bridge approach slabs should be utilized at bridge abutments, the total factored settlement shall be compared to a limit settlement of 3 inches. If the total factored settlement exceeds this value, bridge approach slabs are likely to prove cost effective.
321.1.4 References
Loehr, J.E., C.A. Finley, and D. Huaco (2006), Procedures for Design of Earth Slopes Using LRFD, Final Report to Missouri Department of Transportation, Research Investigation RI03-030.
MCHRP 75-1
MCHRP 79-1
Reese, L.C., W.M. Isenhower, and S-T Wang (2006), Analysis and Design of Shallow and Deep Foundations, John Wiley and Sons, 574 pp.





















![{\displaystyle \delta _{R}={\frac {H_{0}}{1+e_{0}}}{\Bigg [}{\frac {c_{r}}{\phi _{r}}}log{\big (}{\frac {\phi _{p}\sigma '_{p}}{\sigma _{0}}}{\big )}+{\frac {c_{c}}{\phi _{c}}}log{\big (}{\frac {\sigma '_{f}}{\phi _{p}\sigma '_{p}}}{\big )}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27942069f16d2a26c93aef15efc6b3c996badcd5)
![{\displaystyle \delta _{R}={\frac {H_{0}}{1+e_{0}}}{\Bigg [}{\frac {c_{r}}{\phi _{r}}}log{\big (}{\frac {\phi '_{f}}{\sigma '_{0}}}{\big )}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c837c36f3b1ecbf99e41bf1c3777eeaaec70542)
![{\displaystyle \delta _{R}={\frac {H_{0}}{1+e_{0}}}{\Bigg [}{\frac {c_{c}}{\phi _{c}}}log{\big (}{\frac {\phi '_{f}}{\sigma '_{0}}}{\big )}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba4446f59ae40596583eedecbd7421721b3ddbf0)