750.4 Storm Sewers
Contents
- 1 750.4.1 General
- 2 750.4.2 Drainage System Layout Criteria
- 3 750.4.3 Time of Concentration and Discharge
- 4 750.4.4 Hydraulic Design and Analysis of Storm Drain Conduits
- 5 750.4.5 Design Procedure
- 6 750.4.6 References
750.4.1 General
The purpose of this article is to present criteria and design methods that will govern the location, alignment, type, slope and size of storm water conduits. The peak rate of runoff at each inlet in a storm sewer system is determined using the Rational Method detailed in Hydrologic Analysis. The rate of runoff is determined using the total time of concentration to that point in the system, which may include time to flow to an upstream inlet and travel time from that inlet through the upstream portions of the storm sewer system to the inlet in question. After the peak rate of runoff arriving at each inlet has been established, the storm drain conduits can be designed to carry this discharge.
750.4.2 Drainage System Layout Criteria
The first step in the design of storm drain systems is the determination of drop inlet and manhole structure location. This determination is not attempted until such time as the pavement drainage (drop inlet) design is complete, and the inlet sizes have been established.
750.4.2.1 Conduit Location
Trunk or main line conduits are located outside the roadway pavement, if practicable. The location of both main line and lateral conduit is given sufficient study to ensure the selection of the most feasible plan. The final location of a conduit system is established in such a manner that its length is a minimum consistent with hydraulic requirements and in such a manner that the entire system is economically designed for both construction and maintenance.
Flowline depth or vertical location of conduit is generally determined by size of conduit and slope requirements. However, such factors as lateral connections and vertical clearance of obstructions must also be considered in the determination of flowline depth. A minimum depth of cover of 3.0 ft. is recommended. In no case shall the depth of cover be less than 1.0 ft. When a conduit is located under the pavement, the top of the conduit is held to a depth of at least 6 in. below the bottom of the base course. The maximum depth of cover is controlled by fill and other dead loads.
750.4.2.2 Conduit Alignment
Since hydraulic losses are affected by changes in alignment, any change in alignment between connected structures is avoided, if possible. This is especially true on trunk or main line segments of a storm sewer system. Curved alignment is permissible for conduit of 30 in. or more in diameter. Long radius bends are available from many suppliers and are the preferable means of changing direction in pipes. The radius of curvature specified should coincide with standard curves available for the type of material being used. Short radius curves may require curved pipe or other special designs. Such design, however, is restricted to unavoidable cases. The alignment of combining lines of conduit is arranged to minimize head loss at the junction. An angular change in alignment of conduit 30 in. or less in diameter is permissible on lateral lines to effect right angle entry into an inlet or manhole.
750.4.2.3 Conduit Type
The permissible types of conduit for storm sewers are concrete box and the pipe types described in Non-Hydraulic Considerations. When elliptical pipe is substituted for round pipe, it is to be of equivalent size and of the same type as the round pipe for which it is substituted.
750.4.2.4 Conduit Slope
As a general rule, a uniform slope is maintained between structures. A break in slope between any two structures is used only when unavoidable. If practicable, storm sewers are designed with conduit slopes sufficient to develop a self-cleaning full-flow velocity of three feet per second or greater. Minimum slopes complying with the above can be calculated using the following form of Manning’s equation:
- Where:
- S = minimum pipe slope, ft/ft
- Ks = constant, 2.88
- n = Manning’s roughness coefficient
- V = average pipe velocity, 3 ft/s
- D = pipe diameter, ft
Minimum slopes meeting the above criteria for concrete pipe with n=0.013 are given in the following table.
| Pipe Diameter (in.) | Minimum Slope (ft/ft) |
|---|---|
| 8 | 0.0075 |
| 10 | 0.0056 |
| 12 | 0.0044 |
| 15 | 0.0032 |
| 18 | 0.0026 |
| 24 | 0.0017 |
| 30 | 0.0013 |
| 36 | 0.0010 |
| 42 | 0.0008 |
| 48 | 0.0007 |
| 54 | 0.0006 |
| 60 | 0.0005 |
| 66 | 0.0005 |
| 72 | 0.0004 |
750.4.2.5 Manholes
Manholes are installed at all changes in pipe grade or size; at changes in pipe alignment where the pipe diameter is 30 inches or less; at all pipe intersections; and at intervals not greater than 400 feet for conduit 15 inches or less in diameter, and 500 feet for conduit 18 inches or more in diameter. Manholes are not placed in traffic lanes.
As a general rule, a drop inlet is not used as a manhole. It is permissible, however, when consistent with good design and in the interest of economy, to construct an inlet to serve as a manhole, provided storm water alone is involved.
750.4.3 Time of Concentration and Discharge
The Rational Method is used to determine the discharge for storm sewer design. The rate of discharge at any point in the storm drain system is not necessarily the sum of the inlet flow rates of all inlets above that section in the storm drain system. It is generally less than this total. The time of concentration is very influential in determining the design discharge using the Rational Method. As the time of concentration grows larger, the rainfall intensity to be used in the design grows smaller.
The time of concentration for pipe sizing is defined as the time required for water to travel from the most hydraulically distant point in the total contributing watershed to the design point. Typically, this time consists of two components: 1) the time for overland and/or gutter flow to reach the inlet, and 2) the time to flow through the storm sewer system to the design point.
In some cases, such as where a small relatively impervious drainage area with a short time of concentration is added to the system, the peak flow may be larger using the shorter time even though the entire drainage area is not contributing. The designer should be alert for unusual conditions and determine which time of concentration controls for each pipe segment.
750.4.4 Hydraulic Design and Analysis of Storm Drain Conduits
After the preliminary locations of inlets, connecting conduits and outfalls have been determined, the next step is determining the discharge to be carried by each conduit and the required conduit size and gradient. This is done by starting at the upstream reach, calculating the discharge and sizing the pipe, then proceeding downstream, reach by reach to the point where the storm drain connects with other drains or the outfall.
At locations where the pipe size increases (drop inlets and manholes), the downstream crown should be lower than the upstream crown by the amount of energy loss in the structure. A preliminary estimate of the energy loss in the structure can be determined using:
- Where:
- Hp = preliminary estimate of energy loss in manhole or inlet box, ft
- Kp = preliminary loss coefficient from the Preliminary Head Loss Coefficient for Manholes and Inlets table below
- Vo = velocity in outlet pipe, ft/s
- g = acceleration due to gravity, 32.2 ft/s2
Note that this method is to be used only for computing appropriate conduit flow lines and is not to be used in the final hydraulic grade line calculations.
| Structure Configuration | Kp |
|---|---|
| Inlet - Straight Run | 0.50 |
| Inlet - Angled Through | |
| 90° | 1.50 |
| 60° | 1.25 |
| 45° | 1.10 |
| 22.5° | 0.70 |
| Manhole - Straight Run | 0.15 |
| Manhole - Angled Through | |
| 90° | 1.00 |
| 60° | 0.85 |
| 45° | 0.75 |
| 22.5° | 0.45 |
After the design flow rate in a conduit has been established the conduit is sized to carry this flow as an open channel. Under this criterion, the conduits are sized to flow full based on analysis by Manning’s Equation. The open channel flow design charts presented in Open Channels can be of great aid in conduit size selection. In general, conduits sized in this manner will have an ultimate capacity greater than the design capacity because of the potential for pressure flow and the resulting hydraulic head that may develop at the manholes and drop inlets.
Although storm water conduits are designed based on open channel flow, they will not operate as open channels during the design event. For this reason, determination of the hydraulic grade line (HGL) through the storm drain system is necessary in order to determine the water surface elevations at critical points such as manholes and drop inlets. Typically, the energy grade line (EGL) is determined first, and then the velocity head (V2/2g) is subtracted to determine the HGL. In general, if the HGL is above the crown of the pipe, pressure flow hydraulic calculations are appropriate. Conversely, if the HGL is below the crown of the pipe, open channel flow calculations are appropriate. A special concern with storm drains operating under pressure flow is that inlet surcharging and possible manhole lid displacement can occur if the HGL rises above the ground surface.
Calculating the HGL through the system begins at the system outfall with determination of the tailwater elevation. Energy losses in pipe runs, junctions, drop inlets and other structures within the storm drain system are then added to determine the EGL at a specific location, and the HGL is found by subtracting the velocity head. If the outfall is an existing storm sewer system, the HGL calculation must begin at the outfall of the existing system and proceed upstream through this in place system, then upstream through the proposed system to the upstream inlet.
750.4.4.1 Tailwater
The tailwater depth must be evaluated carefully. Evaluation of the HGL for a storm sewer system begins at the system outfall with the tailwater elevation. For most design applications, the tailwater will either be above the crown of the outlet or can be considered to be between the crown and critical depth. When the tailwater is above the crown of the pipe, the actual tailwater depth is used. When the tailwater depth can be considered to be between the crown and critical depth, a value of (dc+D)/2 is used, where dc is the critical depth and D is the pipe diameter. An exception to this rule would be for a very large outfall with low tailwater, where it may be appropriate to compute a water surface profile to determine where the water surface will intersect the top of the conduit and full flow calculations can begin. In this case the downstream water surface would be based on critical depth or the design tailwater depth, whichever is higher.
If the outfall channel is a river or stream, it may be necessary to consider the joint or coincidental probability of two hydrologic events occurring at the same time. The relative independence of the discharge from the storm sewer system and the discharge in the receiving channel can be evaluated by a comparison of the two drainage areas. When there is a large difference in the sizes of the two drainage areas, it becomes less likely that any particular storm event would have the same frequency for both drainage areas. The FHWA HEC-22 publication contains additional information on determining frequencies for coincidental occurrence.
750.4.4.2 Exit Loss
The exit loss (Ho) at the outfall is a function of the change in velocity at the outlet of the conduit. For a sudden expansion such as at the outlet of the storm sewer system, the exit loss is:
- Where:
- V = average outlet velocity, ft/s
- Vd = channel velocity downstream of outlet, ft/s
- g = acceleration due to gravity, 32.2 ft/s2
750.4.4.3 Bend Loss
The bend loss (hb) for storm drain design is generally minor but can be evaluated using the formula:
- Where:
- Δ = angle of curvature in degrees
- Vo = velocity in outlet pipe, ft/s
750.4.4.4 Pipe Friction Loss
The major loss in a storm drain system is the friction loss in conduit runs. The head losses due to friction may be determined by the formula:
- Where:
- Hf = friction loss, ft
- Sf = friction slope, ft/ft
- L = length of conduit run, ft
The friction slope is the slope of the hydraulic gradient in for a particular pipe run and may be determined by rewriting the Manning’s equation:
- Where:
- Q = flow rate, cfs
- n = Manning’s roughness coefficient
- KQ = constant, 0.46
- D = conduit diameter, ft
750.4.4.5 Junction Losses
A pipe junction is the connection of a lateral pipe to a larger trunk pipe without the use of a manhole structure. The following form of the momentum equation may be used to determine junction losses:
- Where:
- Hj = junction loss, ft
- Qo, Qi, Q1 = outlet, inlet, and lateral flows, respectively, cfs
- Vo, Vi, V1 = outlet, inlet, and lateral velocities, respectively, ft/s
- ho, hi = outlet and inlet velocity heads, ft
- Ao, Ai = outlet and inlet cross-sectional areas, ft2
- θ = the angle between the lateral inflow and outflow pipes
750.4.4.6 Transition Losses
A transition is a location where a conduit changes size. Typically, transitions should be avoided and access holes should be used when pipe size increases. However, sometimes transitions are unavoidable. Transitions include expansions, contractions or both. In small storm drains, transitions may be confined within access holes. However, in larger storm drains or when a specific need arises, transitions may occur within pipe runs.
750.4.4.6.1 Non-Pressure Flow
Energy losses in expansions or contractions in non-pressure flow can be expressed in terms of the kinetic energy at the two ends. Contraction and expansion losses for non-pressure flow in pipes can be evaluated with the following equations:
- Hc = Kc [(V22 / 2g) - (V12 / 2g)] (Contraction)
- He = Ke [(V22 / 2g) - (V12 / 2g)] (Expansion)
- where:
- Kc = Contraction Coefficient
- Ke = Expansion Coefficient
- V1 = Velocity Upstream of Transition
- V2 = Velocity Downstream of Transition
- g = Acceleration Due to Gravity, ft/s2,
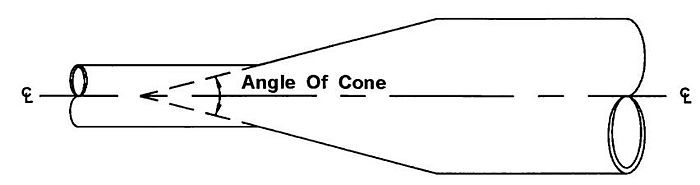
| Typical Values for Ke for Gradual Expansion of Pipes in Non-Pressure Flow (Kc = 0.5Ke) | |||||||
|---|---|---|---|---|---|---|---|
| D2/D1 | Angle of Cone | ||||||
| 10° | 20° | 45° | 60° | 90° | 120° | 180° | |
| 1.5 | 0.17 | 0.40 | 1.06 | 1.21 | 1.14 | 1.07 | 1.00 |
| 3 | 0.17 | 0.40 | 0.86 | 1.02 | 1.06 | 1.04 | 1.00 |
| D2/D1 = Ratio of diameter of larger pipe to smaller pipe. | |||||||
| Typical Values of Kc for Sudden Pipe Contractions | |
|---|---|
| D2/D1 | Kc |
| 0.2 | 0.5 |
| 0.4 | 0.4 |
| 0.6 | 0.3 |
| 0.8 | 0.1 |
| 1.0 | 0.0 |
| D2/D1 = Ratio of diameter of smaller pipe to larger pipe. | |
750.4.4.6.2 Pressure Flow
750.4.4.6.2.1 Expansions
Energy losses in expansions functioning under pressure flow can be evaluated with the following equation:
- He = Ke(V2/2g)
- where:
- Ke = Expansion Coefficient
- V = Velocity Upstream of Transition
- g = Acceleration Due to Gravity, ft/s2
| Values of Ke for Determining Loss of Head due to Gradual Expansions in Pipes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| D2/D1 | Angle of Cone | ||||||||||
| 2° | 6° | 10° | 15° | 20° | 25° | 30° | 35° | 40° | 50° | 60° | |
| 1.1 | 0.01 | 0.01 | 0.03 | 0.05 | 0.10 | 0.13 | 0.16 | 0.18 | 0.19 | 0.21 | 0.23 |
| 1.2 | 0.02 | 0.02 | 0.04 | 0.09 | 0.16 | 0.21 | 0.25 | 0.29 | 0.31 | 0.35 | 0.37 |
| 1.4 | 0.02 | 0.03 | 0.06 | 0.12 | 0.23 | 0.30 | 0.36 | 0.41 | 0.44 | 0.50 | 0.53 |
| 1.6 | 0.03 | 0.04 | 0.07 | 0.14 | 0.26 | 0.35 | 0.42 | 0.47 | 0.51 | 0.57 | 0.61 |
| 1.8 | 0.03 | 0.04 | 0.07 | 0.15 | 0.28 | 0.37 | 0.44 | 0.50 | 0.54 | 0.61 | 0.65 |
| 2.0 | 0.03 | 0.04 | 0.07 | 0.16 | 0.29 | 0.38 | 0.46 | 0.52 | 0.56 | 0.63 | 0.68 |
| 2.5 | 0.03 | 0.04 | 0.08 | 0.16 | 0.30 | 0.39 | 0.48 | 0.54 | 0.58 | 0.65 | 0.70 |
| 3.0 | 0.03 | 0.04 | 0.08 | 0.16 | 0.31 | 0.40 | 0.48 | 0.55 | 0.59 | 0.66 | 0.71 |
| ∞ | 0.03 | 0.05 | 0.08 | 0.16 | 0.31 | 0.40 | 0.49 | 0.46 | 0.60 | 0.67 | 0.72 |
| D2/D1 = Ratio of diameter of larger pipe to diameter of smaller pipe. | |||||||||||
| Values of Ke for Determining Loss of Head due to Sudden Expansions in Pipes | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D2/D1 | Velocity, V, in feet per second | ||||||||||||
| 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 10.0 | 12.0 | 15.0 | 20.0 | 30.0 | 40.0 | |
| 1.2 | 0.11 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.08 |
| 1.4 | 0.26 | 0.26 | 0.25 | 0.24 | 0.24 | 0.24 | 0.24 | 0.23 | 0.23 | 0.22 | 0.22 | 0.21 | 0.20 |
| 1.6 | 0.40 | 0.39 | 0.38 | 0.37 | 0.37 | 0.36 | 0.36 | 0.35 | 0.35 | 0.34 | 0.33 | 0.32 | 0.32 |
| 1.8 | 0.51 | 0.49 | 0.48 | 0.47 | 0.47 | 0.46 | 0.46 | 0.45 | 0.44 | 0.43 | 0.42 | 0.41 | 0.40 |
| 2.0 | 0.60 | 0.58 | 0.56 | 0.55 | 0.55 | 0.54 | 0.53 | 0.52 | 0.52 | 0.51 | 0.50 | 0.48 | 0.47 |
| 2.5 | 0.74 | 0.72 | 0.70 | 0.69 | 0.68 | 0.67 | 0.66 | 0.65 | 0.64 | 0.63 | 0.62 | 0.60 | 0.58 |
| 3.0 | 0.83 | 0.80 | 0.78 | 0.77 | 0.76 | 0.75 | 0.74 | 0.73 | 0.72 | 0.70 | 0.69 | 0.67 | 0.65 |
| 4.0 | 0.92 | 0.89 | 0.87 | 0.85 | 0.84 | 0.83 | 0.82 | 0.80 | 0.79 | 0.78 | 0.76 | 0.74 | 0.72 |
| 5.0 | 0.96 | 0.93 | 0.91 | 0.89 | 0.88 | 0.87 | 0.86 | 0.84 | 0.83 | 0.82 | 0.80 | 0.77 | 0.75 |
| 10.0 | 1.00 | 0.99 | 0.96 | 0.95 | 0.93 | 0.92 | 0.91 | 0.89 | 0.88 | 0.86 | 0.84 | 0.82 | 0.80 |
| ∞ | 1.00 | 1.00 | 0.98 | 0.96 | 0.95 | 0.94 | 0.93 | 0.91 | 0.90 | 0.88 | 0.86 | 0.83 | 0.81 |
| D2/D1 = Ratio of diameter of larger pipe to smaller pipe. | |||||||||||||
750.4.4.6.2.2 Contractions
Energy losses in sudden contractions functioning under pressure flow can be evaluated with the following equation:
- Hc = Kc(V2/2g)
- where:
- Kc = Contraction Coefficient
- V = Velocity Downstream of Transition
- g = Acceleration Due to Gravity, ft/s2
| Values of Ke for Determining Loss of Head due to Sudden Contraction | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D2/D1 | Velocity, V, in feet per second | ||||||||||||
| 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 10.0 | 12.0 | 15.0 | 20.0 | 30.0 | 40.0 | |
| 1.1 | 0.03 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.05 | 0.05 | 0.06 |
| 1.2 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.08 | 0.08 | 0.08 | 0.09 | 0.10 | 0.11 |
| 1.4 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.18 | 0.18 | 0.18 | 0.18 | 0.19 | 0.20 |
| 1.6 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.25 | 0.25 | 0.24 |
| 1.8 | 0.34 | 0.34 | 0.34 | 0.34 | 0.34 | 0.34 | 0.33 | 0.33 | 0.32 | 0.32 | 0.32 | 0.29 | 0.27 |
| 2.0 | 0.38 | 0.38 | 0.37 | 0.37 | 0.37 | 0.37 | 0.36 | 0.36 | 0.35 | 0.34 | 0.33 | 0.31 | 0.29 |
| 2.2 | 0.40 | 0.40 | 0.40 | 0.39 | 0.39 | 0.39 | 0.39 | 0.38 | 0.37 | 0.37 | 0.35 | 0.33 | 0.30 |
| 2.5 | 0.42 | 0.42 | 0.42 | 0.41 | 0.41 | 0.41 | 0.40 | 0.40 | 0.39 | 0.38 | 0.37 | 0.34 | 0.31 |
| 3.0 | 0.44 | 0.44 | 0.44 | 0.43 | 0.43 | 0.43 | 0.42 | 0.42 | 0.41 | 0.40 | 0.39 | 0.36 | 0.33 |
| 4.0 | 0.47 | 0.46 | 0.46 | 0.46 | 0.45 | 0.45 | 0.45 | 0.44 | 0.43 | 0.42 | 0.41 | 0.37 | 0.34 |
| 5.0 | 0.48 | 0.48 | 0.47 | 0.47 | 0.47 | 0.46 | 0.46 | 0.45 | 0.45 | 0.44 | 0.42 | 0.38 | 0.35 |
| 10.0 | 0.49 | 0.48 | 0.48 | 0.48 | 0.48 | 0.47 | 0.47 | 0.46 | 0.46 | 0.45 | 0.43 | 0.40 | 0.36 |
| ∞ | 0.49 | 0.49 | 0.48 | 0.48 | 0.48 | 0.47 | 0.47 | 0.47 | 0.46 | 0.45 | 0.44 | 0.41 | 0.38 |
| D2/D1 = Ratio of diameter of larger pipe to smaller pipe. | |||||||||||||
750.4.4.7 Manhole and Inlet Losses
The head loss encountered in going from one pipe to another through a manhole or inlet is commonly represented as being proportional to the velocity head at the outlet pipe. Using K to signify this constant of proportionality, the energy loss is approximated as:
- Where:
- Hi = head loss through manhole or inlet
- K = adjusted loss coefficient
- Vo = velocity in outlet pipe
- g = acceleration due to gravity
The loss coefficient (K) is dependent on several different factors and can be approximated by the following equation when the inflow pipe invert is below the water level in the manhole or inlet box:
- Where:
- Ko = initial head loss coefficient based on manhole size
- CD = correction factor for pipe diameter (pressure flow only)
- Cd = correction factor for flow depth (non-pressure flow only)
- CQ = correction factor for relative flow
- Cp = correction factor for plunging flow
For cases where the inlet pipe invert is above the water level in the manhole or inlet box, the outflow pipe will function as a culvert, and the procedures in Culverts can be used to determine the water surface elevation (HGL) in the manhole or inlet box.
750.4.4.7.1 Relative Manhole Size
Ko is estimated as a function of the relative manhole size and the angle of deflection between the inflow and outflow pipes.
- Where:
- θ = angle between inflow and outflow pipes
- b = manhole or inlet diameter, ft
- Do = outlet pipe diameter, ft
750.4.4.7.2 Pipe Diameter
A change in head loss due to differences in pipe diameter is only significant in pressure flow situations when the depth in the access hole to outlet pipe diameter ratio (d/Do) is greater than 3.2. Therefore, it is only applied in such cases.
- Where:
- Do = outgoing pipe diameter, ft
- Di = incoming pipe diameter, ft
750.4.4.7.3 Flow Depth
The correction factor for flow depth is significant only in cases of free surface flow when the d/Do ratio is less than 3.2 and is only applied in such cases. Water depth in the access hole is approximated as the level of the hydraulic grade line at the upstream end of the outlet pipe. The correction factor for flow depth (Cd) is calculated by the following:
- Where:
- d = water depth in manhole or inlet above outlet pipe, ft
- Do = outlet pipe diameter, ft
750.4.4.7.4 Relative Flow
The correction factor for relative flow (CQ) is a function of the angle of incoming flow as well as the percentage of flow coming in through the pipe of interest versus other incoming pipes. It is computed as follows:
- Where:
- θ = angle between inflow and outflow pipes
- Qi = flow in the inflow pipe, cfs
- Qo = flow in the outflow pipe, cfs
750.4.4.7.5 Plunging Flow
The correction factor for plunging flow (Cp) corresponds to the effect of another inflow pipe or surface flow from an inlet, plunging into the manhole or inlet box, on the inflow pipe for which the head loss is being calculated. The correction factor is calculated by the following:
- Where:
- h = vertical distance of plunging flow from flow line of incoming pipe to center of outlet pipe, ft
- Do = outlet pipe diameter, ft
- d = water depth in manhole or inlet, ft
750.4.4.8 Freeboard
The calculated water surface elevation (HGL) must be at least one foot below the intake of drop inlets and at least two feet below the top of manhole covers. If these criteria are not met, appropriate adjustments in conduit size and or structure depth are made until the water surface elevations are within allowable limits.
750.4.5 Design Procedure
The following eight-step procedure is to be used in the design of storm sewer systems:
1. Determine inlet locations and geometric layout of system.
2. Prepare plan layout of the storm drainage system establishing the following design data:
- a. Location of storm drains.
- b. Direction of flow.
- c. Location of access holes.
- d. Location of existing utilities such as water, gas, or underground cables.
3. Determine drainage areas and runoff coefficients, and a time of concentration to the first inlet. Use the rational method to determine discharge.
4. Determine an initial pipe size by varying the slope and pipe size as necessary to convey the flow as an open channel (Manning’s equation).
5. Calculate travel time in the pipe to the next inlet by dividing pipe length by the velocity. This travel time is added to the time of concentration for a new time of concentration and new rainfall intensity at the next entry point.
6. Calculate the new area (A) and multiply by the runoff coefficient (C). Use the rational method to determine the new discharge. Determine the size of pipe and slope necessary to convey the discharge as open channel flow.
7. Continue this process to the storm drain outlet.
8. Complete the design by calculating the hydraulic grade line as described in Hydraulic Design and Analysis of Storm Drain Conduits and checking freeboard in manholes and drop inlets. Adjust the system as necessary to meet the freeboard requirements.
750.4.6 References
AASHTO, 2014, AASHTO Drainage Manual, 1st Edition, American Association of State Highway and Transportation Officials..
Federal Highway Administration, 1996, Urban Drainage Design Manual – Hydraulic Engineering Circular 22 (HEC-22), Report No. FHWA-SA-96-078.
Brown, S.A., etal., Urban Drainage Design Manual – Hydraulic Engineering Circular No. 22 (HEC-22), Federal Highway Administration, 3rd Edition, Publication No. FHWA-NHI-10-009, 2009


![{\displaystyle H_{o}=1.0\left[{\frac {V^{2}}{2g}}-{\frac {V_{d}^{2}}{2g}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c373f31a7fbd4e75533f3c2d2a44ada57d760ef)
![{\displaystyle h_{b}=0.0033\Delta \left[{\frac {V_{o}^{2}}{2g}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/795c46fe53f65c2c5b68bd0276666eca07342b78)

![{\displaystyle S_{f}=\left[{\frac {Qn}{K_{Q}D^{2.67}}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be04ed8e7e2a7bb06b53e1a3a6f40661db536296)