106.3.2.78 TM-78, Los Angeles Abrasion for Lightweight Aggregate
This test method determines the resistance to degradation of lightweight aggregate by abrasion and impact in the Los Angeles Machine.
106.3.2.78.1 Apparatus
1) Los Angeles Machine – As described in AASHTO T 96 (ASTM C 131-01 Section 6).
2) Sieves – Conforming to ASTM E 11.
3) Balance - Accurate to within 0.1 percent of the test load over the range required for this test.
4) Oven – A ventilated oven capable of maintaining the temperature at 110°±5º C (230 ± 9º F).
5) Charge – The charge shall consist of steel spheres having diameters averaging approximately 46.8mm (1 27/32 in.) and each having a mass between 390-445 g.
| Grading | Number of Spheres | Mass of Charge, g |
|---|---|---|
| A | 6 | 2500 ± 12 |
| B | 5 | 2090 ± 11 |
| C | 4 | 1670 ± 10 |
| D | 3 | 1250 ± 8 |
106.3.2.78.2 Procedure for Lightweight Aggregate
106.3.2.78.2.1 Sampling
Obtain the field sample in accordance with the Practice AASHTO T2, and reduce the field sample to adequate sample size in accordance with Practice AASHTO T 248.
106.3.2.78.2.2 Preparation
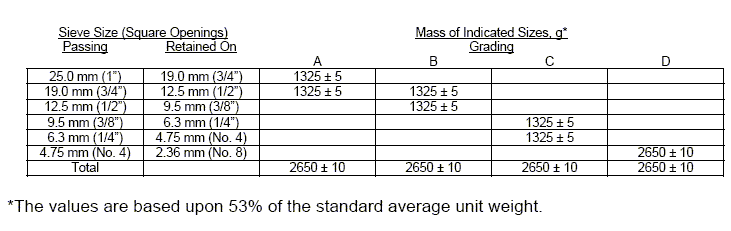
Wash and oven dry the reduced sample at 110° ± 5º C (230° ± 9º F) to substantially constant mass, separate into individual size fractions, and recombine to the grading of Table 106.3.2.78.2.2 most nearly corresponding to the range of sizes in the aggregate as furnished for the work. Record the mass of the sample prior to test to the nearest 1 g.
106.3.2.78.2.3 Test
Place the test sample and the charge in the Los Angeles testing machine and rotate the machine at a speed of 30 to 33 r/min for 500 revolutions. After the prescribed number of revolutions, discharge the sample from the machine and make a preliminary separation of the sample on a sieve coarser than the 1.70-mm (No. 12). Sieve the finer portion on a 1.70 mm sieve in a manner conforming to Test Method AASHTO T 27. Wash the material coarser than the 1.70-mm sieve and oven-dry at 110° ± 5° C (230° ± 9° F).
If the aggregate is essentially free of adherent coatings and dust, the requirement for washing after test may be waived, but drying before the test is always required. However in case of referee testing, the washing procedure shall be performed.
106.3.2.78.3 Calculations
Calculate the loss (difference between the original mass and the final mass of the test sample) as a percentage of the original mass of the test sample.
106.3.2.78.4 Report
Report the loss by abrasion and impact of the sample expressed to the nearest 1% by mass; and report grading of material, A, B, C or D.