751.22 Prestressed Concrete I Girders
| Video |
| Concrete Girder |
751.22.1 General
751.22.1.1 Material Properties
Concrete
Conventional concrete strength for P/S I-Girder shall be the following:
- For MoDOT Standard Girders:
- ,
- Optional higher concrete strength shall be:
- ,
- OR
- With the approval of the Structural Project Manager or Liaison:
- ,
- For NU Standard Girder:
- ,
- Strengths greater than 8 ksi shall require high performance concrete (HPC) and may increase costs due to production modifications necessary to obtain the required strength.
- Modulus of Elasticity,
- Where,
- f'c in ksi
- K1 = correction factor for source of aggregate
- = 1.0 unless determined by physical testing
- K1 = correction factor for source of aggregate
| Prestressing strand | ||
|---|---|---|
| Type of strand: | ||
| AASHTO M203 (ASTM A416) Grade 270 | ||
| Uncoated, seven-wire, low-relaxation strand | ||
| Ultimate tensile strength, | ||
| Yield strength, | ||
| Strand modulus of elasticity, | ||
| For standard concrete: | ||
| Strand diameter, | ||
| Strand area, | ||
| For optional concrete: | ||
| Strand diameter, | ||
| Strand area, | ||
| Mild reinforcing steel | ||
| Minimum yield strength, | ||
| Steel modulus of elasticity, | ||
| Welded Wire Reinforcement | ||
| Minimum yield strength, | ||
| Steel modulus of elasticity, | ||
751.22.1.2 Geometric Dimensions
The ratio of the depth of girder to span length will in general be not less than 1/18.
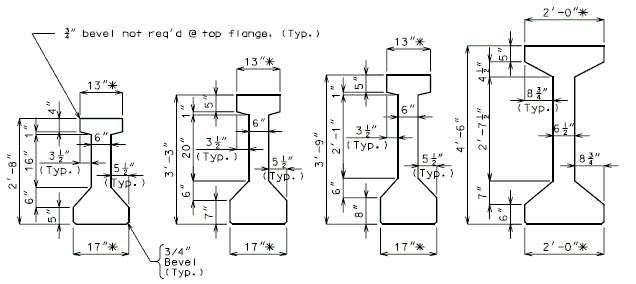
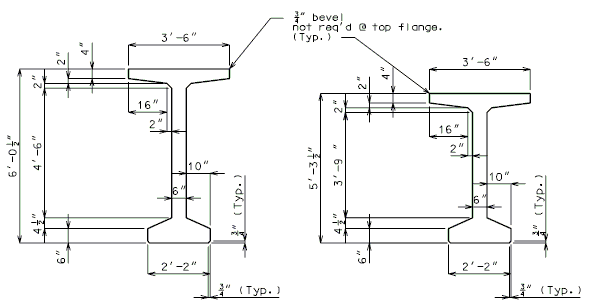
The cross sectional dimensions of the girder shall be one of the following:
- MoDOT Standard Girders:
| BEAM TYPE 2 | BEAM TYPE 3 | BEAM TYPE 4 | BEAM TYPE 6 |
| BEAM TYPE 7 | BEAM TYPE 8 |
If the web is required to be increased, then the top and bottom flanges are to be increased by the same amount. (1" increments 2" max.).
See Structural Project Manager before using NU Sections.
- NU Standard Girders:
751.22.1.3 Typical Span Ranges
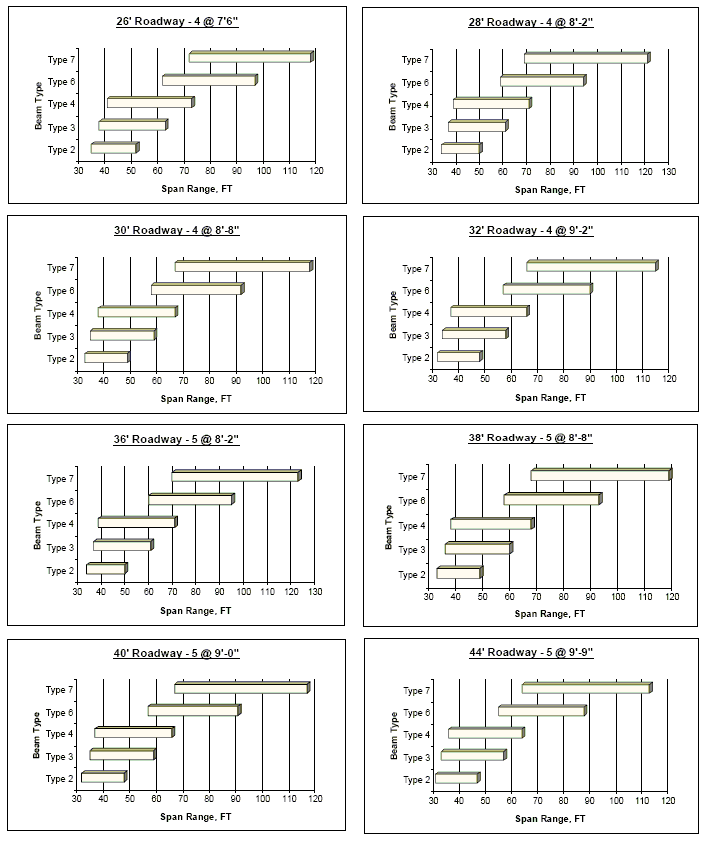
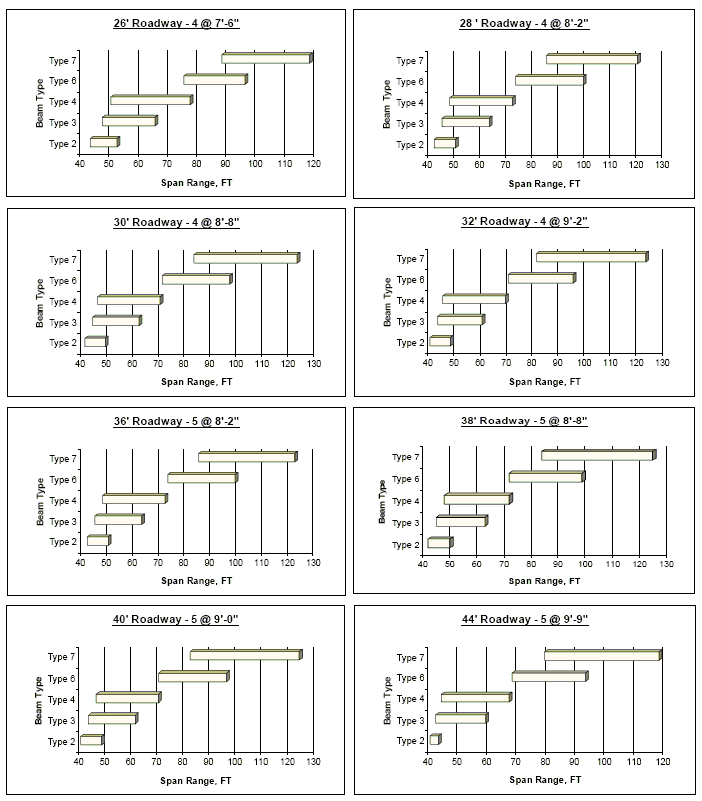
The following charts provide span ranges (limits) for P/S I-girders based on girder spacing and standard roadway widths.
Limitations of the Charts:
- A. Standard Concrete Charts Only
- Criteria used in determining maximum span lengths for lower conventional concrete strength:
- 1) Low-relaxation strand with 0.5” strand diameter
- 2) Concrete strengths, = 4.5 ksi and = 6.0 ksi
- 3) 3-span bridge consisting of 3 equal length girders made continuous and composite
- B. Optional Concrete Charts Only
- Criteria used in determining maximum span lengths for greater conventional concrete strength:
- 1) Low-relaxation strand with 0.6” strand diameter
- 2) Concrete strengths, = 5.0 ksi and = 7.0 ksi
- 3) 3-span bridge consisting of 3 equal length girders made continuous and composite
- C. Both Standard Concrete and Optional Concrete Charts
- Criteria used in determining span ranges for both Standard and Optional Concrete conventional strengths.
- 1) Minimum span lengths were determined by the positive moment capacity of the smallest strand arrangement per beam shape. Shorter span lengths are possible.
- 2) Based on 10 ft. design lanes. (Current design practice meets AASHTO LRFD and uses 12 ft. design lanes.)
- 3) Based on unrefined prestress loss equations. (Current design practice meets AASHTO LRFD and uses refined losses.)
Recommended Adjustments for Using the Charts:
Because the span limit charts were developed using older design criteria as noted above, increased span lengths are probable.
- 1) Span limits given in all charts should be increased 10 percent to account for current design practice. Ten percent can safely be used without a preliminary girder analysis.
- 2) Span limits given in all charts shall be increased when a preliminary girder analysis based on actual design conditions is performed which shall be noted on the Design Layout.
| Span range charts are planned for future replacement. Use the recommended adjustments until implemented. |
Given Roadway Widths and Girder Spacing
Given Roadway Widths and Girder Spacing
751.22.1.4 Span and Structure Lengths
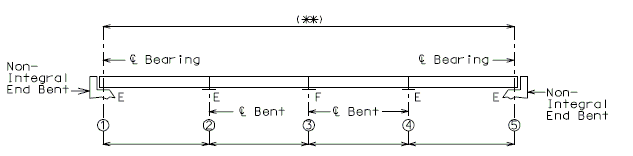
Girder Length and Geometric Layout
- Tangent Bridges
- Girder lengths of exterior spans (i.e., end spans) shall be computed using the requirements shown below.
- Girder lengths of interior spans shall be computed using the requirements shown below.
- Curved Bridges
- Layout of any curved structure may be done using any coordinate geometry programs available. To layout the bridge, use the following steps:
- Start out by laying in the centerline (CL) of the survey curve.
- Locate the tie point of the bridge. This point will usually be on the CL of the survey curve but may be on a baseline which is offset a certain distance to the CL of the survey curve.
- A second tie point may be required if the skew is not measured to the CL of roadway at the bridge tie point. If this is the case, establish the tie point at the specified station and plot the skew line at the required angle.
- Next, on the centerline of structure or baseline curve, locate the station of the CL of bent for each intermediate bent and the fill face for the end bents. Once these points are located, plot lines through these stations parallel to skew line. Normally the layout file will specify that all bents are parallel to the skew line; however, there may be times when the bents are radial or have varying skews.
- When locating the stations in the preceding step, the distance between CL of intermediate bents are exactly the layout lengths specified on the file. However, the end spans need to follow the procedure for calculating length set forth in this section.
- When the CL of the intermediate bents and the fill face lines have been added, chords should be drawn connecting these points sequentially. For example, if you have a three span bridge, chords should be drawn from the fill face of bent 1 to CL of bent 2, CL bent 2 to CL bent 3, and CL bent 3 to fill face bent 4.
- When all the chords are in, offset each girder in each span parallel to this chord. The perpendicular distance between girders will be the same for all spans, but the skew distance between girders along the bent will vary from bent to bent depending on the skew to the CL at that point. The designer needs to be aware of the fact that at an intermediate bent the distance between bearings on the approaching and leaving span sides will be different distances. These bearings will not line up across the bent and will actually diverge more the farther away they are from the CL of the survey.
- When establishing the CL of bearing points, the designer needs to allow for a minimum of seven (7) inches between ends of girders at the bents while keeping in mind that the girders will be offset and at different skews. If the offset is greater than half the girder bottom flange width, see Structural Project Manager. The distance from the end of girder to CL of bearing point should be half of the bearing length plus one inch minimum clearance. Once the distance for CL bent to CL of bearing is calculated, the designer should offset lines by that dimension on either side of the CL of bent. These lines will then be intersected with each of the girder lines to create the bearing points on each bent.
- Between the bearing points at the ends of the girders, quarter points or tenth points need to be established, depending on the girder span. These points will be used in calculating the haunch and bottom of slab elevations for the bridge deck.
- The bridge deck and barrier curbs can be laid in by offsetting the CL of roadway to each side by the proper distance. Curves should be laid in to designate both the inside and outside edges of the barrier curb. These will later be useful in laying in the wings and end bents.
- After the outside edge of slab curves are plotted, the curve offsets need to be found. The intersection point of the outside edge of slab and the CL of each bent or fill face can be connected with chords. The distance between these chords and their partner curves need to be calculated at five foot intervals beginning at the center point of each chord.
- Joints are placed in the barrier curb at each bent. These joints are placed perpendicular to the CL of the roadway through the intersection point of the CL bent and the inside of barrier curb.
- Wing layout length is given on the profile sheets in the layout file. An arc should be struck so as to intersect the inside of barrier curb the specified length from a point at the intersection of the fill face and the inside of barrier curb. This point will mark the end of the wing which is perpendicular to the CL of the roadway.
- The vertical curve information needs to be added so a program can calculate the elevations at the desired stations. After this is done, the designer can request any of the following information which will be needed:
- Stations and elevations of all points
- Offset distances to the chords
- Lengths of girders
- Distances between bearings
- Angles between girders and each bent
- Lengths of bents
- Lengths of barrier curbs between joints
- Minimum vertical clearance


- Note: Layout length for single span shall be measured from centerline of bearing to centerline of bearing. If the difference between layout length of the end span and interior span is within 1 ft., then layout length should be adjusted if possible so the girder lengths are equal for end span and interior span.
- (*) Minimum dimension from edge of bearing pad to end of girder equals one inch.
- (**) Design layout lengths are horizontal lengths. Girder lengths should be adjusted according to grade and shall be specified to the nearest 1/8 inch.
- (***) For large skews, end bent beam caps may need to be larger to provide edge distance.
- (****) Horizontal distance along certerline of girder.

Note: Non-Integral end bents with skews greater than 40° shall always have girder ends coped. Skews less than 40° shall have girder ends coped on case by case basis. It is preferable to not cope across the web.
Check clearance from fill face of integral end bents to bottom flanges of NU standard girders. Maintain 3” (min.) clearance. Coping may be permitted with approval of the Structural Project Manager or Structural Liaison Engineer.

(INTEGRAL END BENTS)
(NON-INTEGRAL END BENTS)
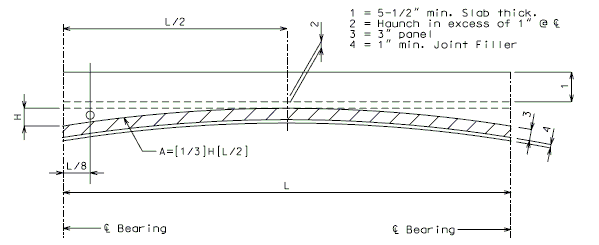
751.22.1.5 Constant and Varied Joint Filler Loads
Varied joint filler load
The prestressed I-girder should first be designed assuming that the contractor will vary the joint filler supporting the panels on the girder flange. This assumption will maintain the minimum slab/panel combination thickness of 8 1/2”, and will eliminate the possibility of increased load due to varying slab thickness.
Constant joint filler load
With the girder designed and the camber and haunching dimensions calculated, the girder should be checked assuming the contractor will use a constant 1” joint filler. This will cause the slab thickness to vary due to camber of the girder, increasing load. This additional load shall be placed as a concentrated load at 1/8 point from each end of the girder.
An example of how this concentrated load could be calculated is shown as follows:
- Load
- Determine the concentrated load* to girders by distributing w transversely across the girders. If the minimum haunch is greater than 1” joint filler, the additional haunch shall be included in the slab thickness as a uniform load. If the use of these loads causes the girder design to change, it shall be the responsibility of the designer to determine if the camber and haunching should be recalculated.
This load shall be positioned at the 1/8 point from centerline of bearing pad.
The girder and bearing designs should be checked for the constant joint filler option and constant joint filler load. However, camber, haunching and beam seat elevations shown on the plans should be based on the variable joint filler option.
751.22.2 Design
751.22.2.1 Load Combinations
In general, each component shall satisfy the following equation:
Where:
| = Total factored force effect | |
| = Force effect | |
| = Load modifier | |
| = Load factor | |
| = Resistance factor | |
| = Nominal resistance | |
| = Factored resistance |
- Limit States
The following limit states shall be considered for P/S Girder design:
- SERVICE I - for compressive stress
- SERVICE III - for tensile stress
- STRENGTH I
See LRFD Table 3.4.1-1 for Loads and Load Factors applied at each given limit state.
- Resistance factors,
STRENGTH limit states, see LRFD Article 6.5.4.2 & 5.5.4.2.1
For all other limit states, = 1.00
See EPG 751.2.3.1 Load Modifiers.
751.22.2.2 Prestressing Strands
Transfer Length of Prestressing Strands
The prestressing force may be assumed to vary linearly from zero at the point where bonding commences to a maximum at the transfer length. The transfer length may be taken as 60 times the strand diameter.
Development Length of Prestressing Strands
The development length for prestressing strands shall be taken as:
Where: = Nominal diameter of strand, (in.) = Average stress in prestressing strand at the time for which the nominal resistance of the girder is required, (ksi)
Stress limits for prestressing strands
Strand stress at service limit state shall not exceed the following:
At jacking:
- ksi
- (For typical girders and fabrication economy, )
At service limit state after all losses:
- ksi
Where:
| = Stress in prestressing strand at jacking, (ksi) | |
| = Effective stress of strand after all losses, (ksi) | |
| = Yield strength of strand, (ksi) | |
| = Ultimate tensile strength of strand, (ksi) |
Prestress Losses
Refined estimates of time-dependent losses are used, based on AASHTO LRFD Article 5.9.5.4, as opposed to approximate lump sum estimate of losses in AASHTO LRFD Article 5.9.5.3.
The prestress losses shall be calculated to investigate concrete stresses at two different stages.
- Temporary stresses immediately after transfer:
- Final stresses
SERVICE I and SERVICE III Limit states shall be investigated at each stage.
Harped Strands
Harped strands, although they add to the shear strength of the girder, are primarily used to keep the girder stresses (both top and bottom) within allowable limits while developing the full capacity of the girder at midspan.
Harped strands should be held down at points of 0.4 of the distance from each end of the girder.
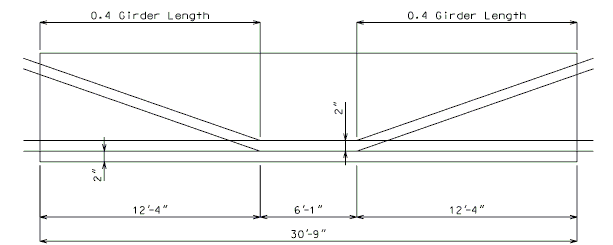
The jacking force applied to prestress strands produces an excessive vertical uplift in short spans on tall girders resulting in failure of harped strand hold-downs. The allowable limits for hold-downs are as follows:
- 5 kip/strand
- 10 kip/bolt
- 42 kip/hold-down
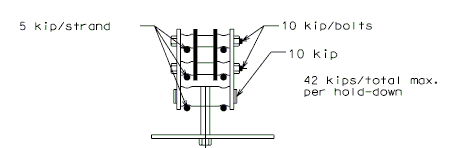
If necessary lower harped strand end location to meet criteria or use straight strands only. Investigate the possibility of using all straight strands when strength check of a hold-down device exceeds allowable.
Straight Strands.
Short spans (<40 ft.) are to use straight strands only for all girders greater than 2'-8" tall. Use at least two straight strands at the top of the girder when straight strands are used. Where straight strands only will not work a single hold-down point may be used. Note: A single point hold-down has twice the uplift force.
Strand Arrangement Optimizing
Using all straight strands for girder lengths less than 70 ft. should be investigated for MoDOT Standard Girder Types 6, 7, 8 and all NU Standard Girders in order to reduce risk of strand or hold-down breakage, increase safety by reducing risk of injury during fabrication and reduce cost.
Consider using the same section for all spans. This permits the use of shorter girders in the casting bed with longer girders, even if straight strands are needed, in the top flanges of the girders. They can be placed at either end of the bed and still optimize the usage of the bed.
Consider using the same number of draped strands for all spans and debond where needed. Strand patterns should be similar between long and short spans. For example, the designer should not use a single column of draped strands on the short spans and two columns of draped strands on the long spans. This will prevent optimization of the bed.
Debonding Strands
In all debonding operations the prestressing forces must be in such a manner as to prevent any sudden or shock loading.
Debonding a strand consists of wrapping the unnecessary strand(s) with a polyethylene plastic sleeve that prevents interaction of the strand with the concrete during casting and release which prevents any prestress force transfer.
751.22.2.3 Flexure
Flexure capacity of prestressed I-girders shall be determined as the following.
Flexural resistance at strength limit state
Where:
| = | Flexural resistance | |
| = | Nominal flexural resistance | |
| = | Total factored moment from Strength I load combination | |
| = | Flexural resistance factor as calculated in LRFD 5.5.4.2 |
Negative moment reinforcement design
P/S I-girder shall be designed as a reinforced concrete section at regions of negative flexures (i.e., negative moments).
At least one-third of the total tensile reinforcement provided for negative moment at the support shall have an embedment length beyond the point of inflection not less than the specified development length of the bars used.
Slab longitudinal reinforcement that contributes to making the precast beam continuous over an intermediate bent shall be anchored in regions of the slab that can be shown to be crack-free at strength limit states. This reinforcement anchorage shall be staggered. Regular longitudinal slab reinforcement may be utilized as part of the total longitudinal reinforcement required.
Effective Slab Thickness
An effective slab thickness shall be used for design by deducting from the actual slab thickness a 1” integral, sacrificial wearing surface.
Design A1 bar in the top flange
The reinforcement A1 shall resist the tensile force in a cracked section computed on the basis of an uncracked section.
Required steel area is equal to:
Where:
| = , allowable tensile stress of mild steel, (ksi) | |
| = Resultant of total tensile force computed on the basis of an uncracked section, (kips) |
Limits for reinforcement
The following criteria shall be considered only at composite stage.
Minimum amount of prestressed and non-prestressed tensile reinforcement shall be such that the factored flexural resistance, Mr, is at least equal to the lesser of:
- , or
Where:
| = | Cracking moment, (kip-in.) | |
| = | Total factored moment from Strength I load combination, (kip-in.) |
751.22.2.4 Shear
Shear capacity of P/S I-girder should be checked along girder length and girder-slab interface.
Shear resistance at strength limit state
Where:
| = | Shear resistance | |
| = | Nominal shear resistance | |
| = | Total factored shear from Strength I load combination | |
| = | Shear resistance factor |
Nominal shear resistance
The nominal shear resistance, , shall be lesser of:
- , or
Where:
Where:
| = | Nominal concrete shear resistance, (kips) | |
| = | Nominal shear reinforcement resistance, (kips) | |
| = | Component of prestressing force in the direction of shear force, (kips) | |
| = | Thickness of web, (in.) | |
| = | Effective shear depth taken as the distance measured perpendicular to the neutral axis, between the resultants of tensile and compressive forces due to flexure, (in.) | |
| = | Spacing of shear reinforcement, (in.) | |
| = | Factor indicating ability of diagonally cracked concrete to transmit tension | |
| = | Angle of inclination of diagonal compressive stress, (degree) | |
| = | 90.0, Angle of inclination of shear reinforcement to a longitudinal axis, (degree) | |
| = | Area of shear reinforcement, (in.2) | |
| = | Minimum yield strength of tension shear reinforcement, (ksi) |
Design sections near supports
Where a reaction force in the direction of the applied shear introduces compression into the end region of girder, the location of the critical section for shear is measured from the internal face of support a distance, dv. Otherwise, the design section shall be taken at the internal face of the support.
Where:
= effective shear depth taken as the distance, measured perpendicular to the neutral axis, between the resultants of the tensile and compressive forces due to flexure; it need not be taken to be less than the greater of 0.9de and 0.72h.
Girder regions requiring shear reinforcement
Girder shear reinforcement, usually consisting of stirrups, shall be provided where:
Where:
| = | Factored shear force from Strength I load combination, (kips) | |
| = | Nominal concrete shear resistance, (kips) | |
| = | Component of prestressing force in the direction of shear force, (kips) | |
| = = |
Shear resistance factor
0.9 for normal weight concrete |
Shear Reinforcement Limits
Minimum reinforcement
Area of shear reinforcement shall not be less than:
Where:
| = | Area of shear reinforcement, (in.2) | |
| = | Thickness of web, (in.) | |
| = | Spacing of shear reinforcement, (in.) | |
| = | Final concrete compressive strength, (ksi) |
Maximum reinforcement
Maximum spacing of shear reinforcement shall be determined as:
If , then
If , then
Where:
| = | Effective shear depth taken as the distance measured perpendicular to the neutral axis, between the resultants of tensile and compressive forces due to flexure, (in.) | |
| = | Shear stress on concrete, (ksi) | |
| = | Maximum spacing of shear reinforcement, (in.) |
Shear stress on concrete shall be determined as:
Where:
| = | Shear stress on concrete, (ksi) | |
| = | Factored shear from Strength I load combination, (kips) | |
| = = |
Shear resistance factor
0.9 for normal weight concrete | |
| = | Thickness of web, (in.) | |
| = | Component of prestressing force in the direction of shear force, (kips) | |
| = | Effective shear depth taken as the distance measured perpendicular to the neutral axis, between the resultants of tensile and compressive forces due to flexure, (in.) | |
| = | ||
| = | Distance from extreme compression fiber to the centroid of tensile force in the tensile reinforcement, (in.) | |
| = | Total height of girder including slab thickness, (in.) |
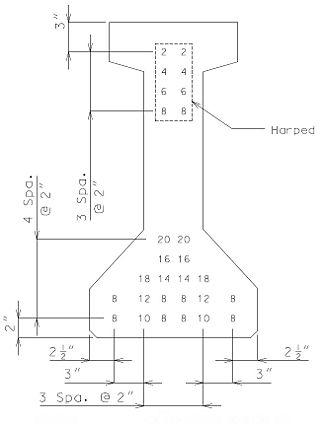
Girder-Slab Interface
The horizontal shear between the girder and slab shall be determined as specified in LRFD 5.8.4.3. The nominal horizontal shear resistance of the interface plane shall be taken as specified in LRFD 5.8.4.1. Minimum interface shear reinforcement shall be provided as specified in LRFD 5.8.4.4. The parameters used in determining the nominal horizontal shear resistance shall be taken as specified for a “cast-in-place concrete slab on clean concrete girder surfaces, free of laitance with surface roughened to an amplitude of 0.25 inch.”
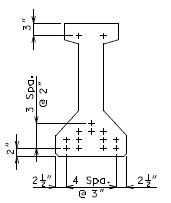
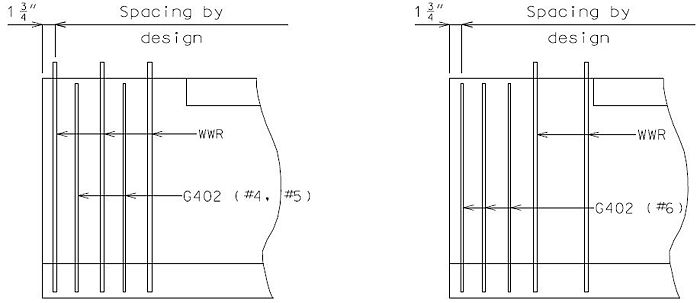
The interface shear shall be resisted by extending and anchoring the vertical shear reinforcement into the slab. If the resistance provided by extending the vertical shear reinforcement is inadequate then additional U-bars may be provided as shown for a MoDOT Standard Girder Type 7 in EPG 751.22.3.6 Girder Reinforcement.
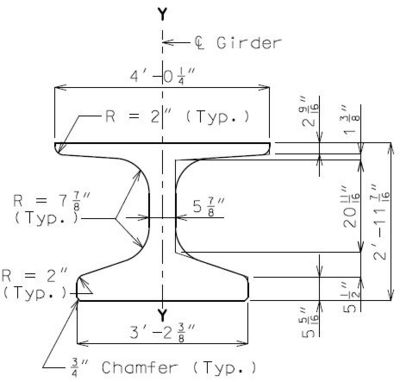
For NU Girders the edges of the top of girder flange are intentionally debonded (see figure below) and shall not be included when determining the nominal horizontal shear resistance. See EPG 751.50 Standard Detailing Notes H2.93 for specifics about the debonded width for NU Girders. Similarly, for all other prestressed girders, the joint filler width supporting precast panels shall be considered debonded and excluded when determining the interface resistance.
Pretensioned anchorage zones
The bursting resistance of anchorage zones provided by vertical reinforcement (i.e., B2 bars, WWF, G402 bars) in the ends of prestressed girders at the service limit state shall be taken as:
Where:
| = | Stress in mild steel not exceeding 20 ksi | |
| = | Total area of vertical reinforcement located within a minimum distance of h/4 from the end of the girder where h is overall depth of precast member as shown below. | |
| = | Prestressing force at transfer |
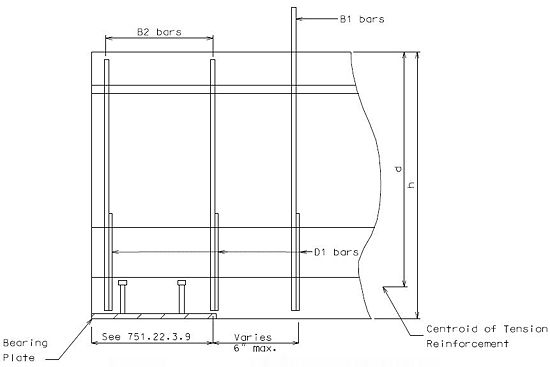
Confinement reinforcement
Reinforcement (i.e., D1 bars or G301 bars, not shown) shown in the figure above shall be placed to confine the prestressing strands in the bottom flange for a minimum distance of 1.5d from the end of beam.
The reinforcement shall not be less than #3 deformed bar, with spacing not exceeding 6.0 inches and shaped to enclose the strands.
MoDOT extends the use of D1 and G301 bars for the full length of girders.
751.22.2.5 Deformations
Criteria for deflection
For investigating maximum absolute deflection, all design lanes shall be loaded, and all supporting components should be assumed to deflect equally.
For composite design, the design cross-section should include the entire width of the roadway and the structurally continuous portions of railings, sidewalks, and median barriers. Note that safety barrier curbs are usually discontinuous over the bents. For skewed bridges, a right cross-section may be used.
Service I load combination shall be used. Dynamic load allowance shall be applied.
See EPG 751.2.4.2 Live Load Deflection Limits.
Calculation of deflection and camber
Deflection and camber calculations shall consider all internal loads (i.e., prestressing, concrete creep, and shrinkage) and external loads such as dead loads and live loads.
Camber is an upward displacement caused by moment due to prestressing forces. Deflection is a downward displacement due to external loads. Therefore, both camber and deflection shall be considered in making an appropriate adjustment for final profile grade on the bridge.
Initial camber at midspan
Total initial camber at transfer due to self-weight of girder and prestressing forces shall be determined as:
Where:
| = Initial camber at transfer | |
| = Deflection due to self-weight of girder | |
| = Camber due to prestressing straight strands | |
| = Camber due to prestressing harped strands | |
| = Camber due to creep |
Note: Positive and negative values indicate downward and upward displacements, respectively.
Final camber at midspan
Total deformation can be determined as the sum of initial camber and deflections due to slab, diaphragm, and creep effect before composite action between slab and girder.
Where:
| = | Deflection due to concentrated loads (haunch, diaphragms) | |
| = | Deflection due to weight of slab |
Final camber along span length
Deformations along the span length can be approximately determined as a product of final camber at midspan times correction factors.
| = | 0.3140 at span fraction of 0.10 | |
| = | 0.5930 at span fraction of 0.20 | |
| = | 0.7125 at span fraction of 0.25 | |
| = | 0.8130 at span fraction of 0.30 | |
| = | 0.9520 at span fraction of 0.40 | |
| = | 1.0000 at span fraction of 0.50 |
Calculation of camber (upward)
Camber at midspan due to strand forces is determined as the following: For straight strands,
Where:
Where:
| = Total prestressing force of straight strands at transfer (including losses due to elastic shortening), (kips) | |
| = Total prestressing force in straight strands due to losses prior to slab placement (kips). Opposite in sign to , typically. | |
| = Distance between centerlines of bearing pads, (in.) | |
| = Initial concrete modulus of elasticity based on , (ksi) | |
| = Final concrete modulus of elasticity based on (ksi) | |
| = Moment of inertia of transformed non-composite section computed based on , (in.4) | |
| = Moment of inertia of transformed non-composite section based on , (in.4) | |
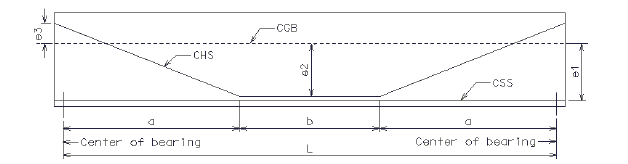
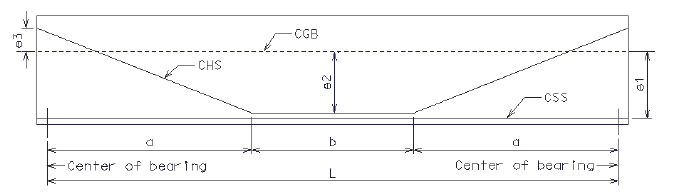
| = Eccentricity between centroid of straight strands (CSS) and center of gravity of transformed non-composite section (CGB) as shown in Figure below, (in.) |
For two-point harped strands,
Where:
Where:
| = Total prestressing force of harped strands at transfer (including loss due to elastic shortening), (kips) | |
| = Total prestressing force of harped strands due to losses prior to slab placement (kips) | |
| = Length between harped points, (in.) | |
| = Eccentricity between centroid of harped strands (CHS) and center of gravity of transformed non-composite section (CGB) at midspan as shown in Figure below, (in.) | |
| = Eccentricity between centroid of harped strands (CHS) and center of gravity of transformed non-composite section (CGB) at the end of girder as shown in Figure below, (in.) |
Calculations of deflections (downward)
Deflections at midspan due to dead loads are determined as the following: For self-weight of girder,
Where:
| = | Uniform load due to self-weight of girder, (kip/in.) |
For self-weight of slab,
Where:
| = | Uniform load due to self-weight of slab, (kip/in.) |
Weight of additional slab haunch may be treated as uniform or concentrated load as appropriate. Diaphragm weight should be treated as concentrated load.
For one concentrated load at midspan,
For two equal concentrated loads,
Where:
| = Concentrated load due to diaphragm and/or additional slab haunch, (kips) | |
| = Distance from the centerline of bearing pad to the applied load, P, (in.) |
Creep coefficient
Research has indicated that high strength concrete (HSC) undergoes less ultimate creep and shrinkage than conventional concrete.
Creep is a time-dependent phenomenon in which deformation increases under a constant stress. Creep coefficient is a ratio of creep strain over elastic strain, and it can be estimated as follows:
| = | |
| = | |
| = | |
| = | |
| = |
Where:
| = Creep coefficient. | |
| = 70, Average annual ambient relative humidity | |
| = Maturity of concrete, (days) Use 90 days for camber design. | |
| = Age of concrete when a load is initially applied, (days) Use 0.75 days for camber design. | |
| = Volume-to-surface area ratio, (in.) | |
| = Initial girder concrete compressive strength, (ksi) |
Where:
| = Moment due to girder weight at mid span. |
751.22.3 Details
751.22.3.1 Reinforcement Criteria
Minimum Concrete Cover
- 2.0" (Min.) to centerline of strands
- 1.0" for stirrups
Minimum Radius of Bar Bend in Stirrups
- 3 through #5 bars = 4.0 x Bar Diameter.
Minimum Spacing of Reinforcement Bars
For precast concrete, the clear distance between parallel bars in a layer shall not be lesser than:
- Nominal Diameter of bar
- 1.33 x Maximum Aggregate Size
- 1.0"
Minimum Spacing of Prestressing Strands
Spacing between each pretressing strand shall not be less than the larger of:
- A clear distance of 1.33 x Maximum Aggregate Size
- Center-to-center spacing of 2" for 0.6" strand diameter
- Center-to-center spacing of 1.75" for 0.5" strand diameter
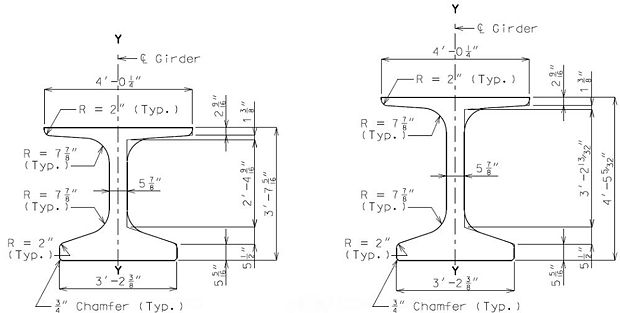
751.22.3.2 MoDOT Standard Girders
751.22.3.2.1 Beam Type 2 Dimensions/Strand Arrangements
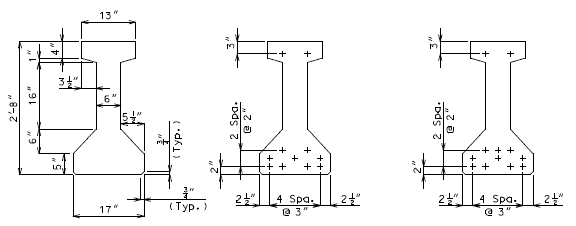
| GIRDERS 2A THRU 2C
= 310.9 SQ. IN. |
GIRDER 2A
(11 STRANDS) |
GIRDER 2B
(12 STRANDS) |
| = 310.9 SQ. IN. = 14.08 IN. |
GROUP I |
 GROUP II |
Numbers shown on girders relate to strand locations. |
ATTENTION: Location of harped strands shown in top flange are at end of girder and harped strands in bottom flange are at centerline.
If the web thickness is required to be increased, then the top and bottom flanges are to be increased by the same amount. (1" increments, 2" max.)
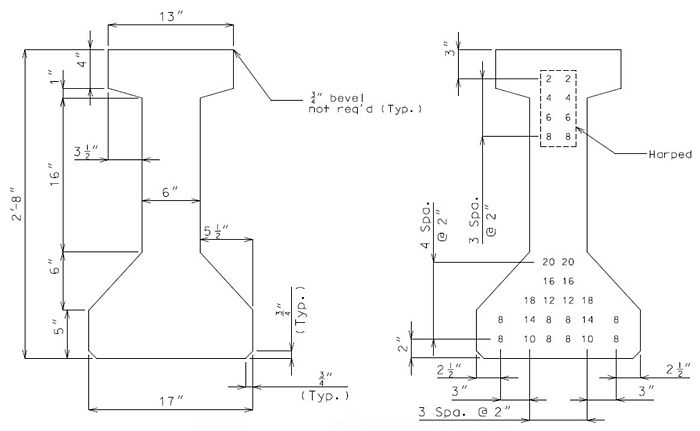
751.22.3.2.2 Beam Type 3 Dimensions/Strand Arrangements
| GIRDERS 3A THRU 3B
= 381.9 SQ. IN. |
GIRDER 3A
(11 STRANDS) |
GIRDER 3B
(12 STRANDS) |
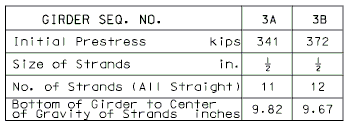
| Note: Investigate the possibility of using all straight strands when strength check of a hold-down device exceeds allowable. All strand arrangements shown on this page have straight strands only. Strand arrangements other than those shown may be investigated by the designer. |
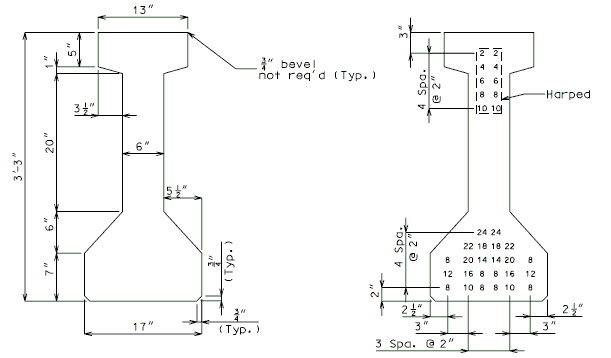
| = 381.9 SQ. IN. = 17.08 IN. |
GROUP I |
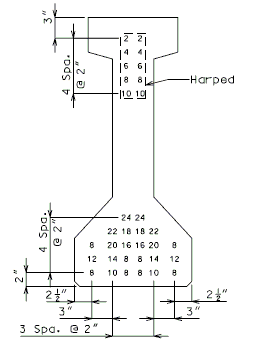 GROUP II |
Numbers shown on girders relate to strand locations. |
ATTENTION: Location of harped strands shown in top flange are at end of girder and harped strands in bottom flange are at centerline.
If the web thickness is required to be increased, then the top and bottom flanges are to be increased by the same amount. (1" increments, 2" max.)
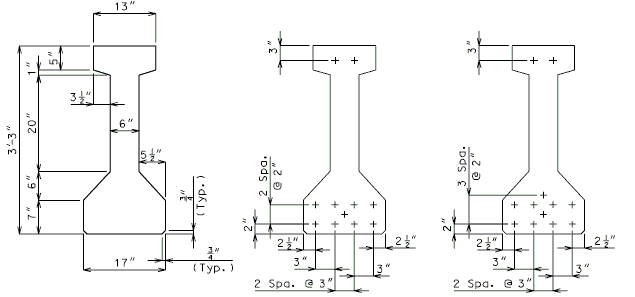
751.22.3.2.3 Beam Type 4 Dimensions/Strand Arrangements
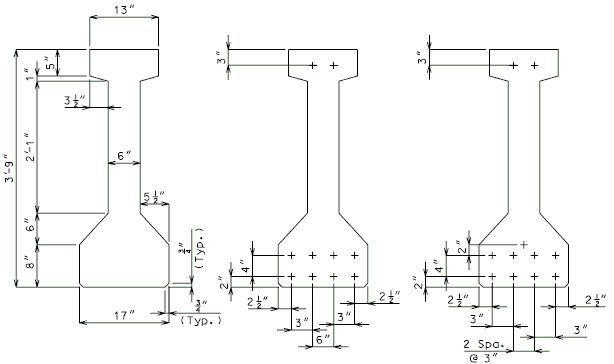
| GIRDERS 4A THRU 4C
= 428.9 SQ. IN. |
GIRDER 4A
(10 STRANDS) |
GIRDER 4B
(11 STRANDS) |
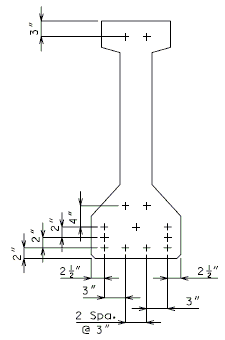 GIRDERS 4C |

|
| = 428.9 SQ. IN. = 19.54 IN. |
GROUP I |
 GROUP II |
Numbers shown on girders relate to strand locations. |
ATTENTION: Location of harped strands shown in top flange are at end of girder and harped strands in bottom flange are at centerline.
If the web thickness is required to be increased, then the top and bottom flanges are to be increased by the same amount. (1" increments, 2" max.)
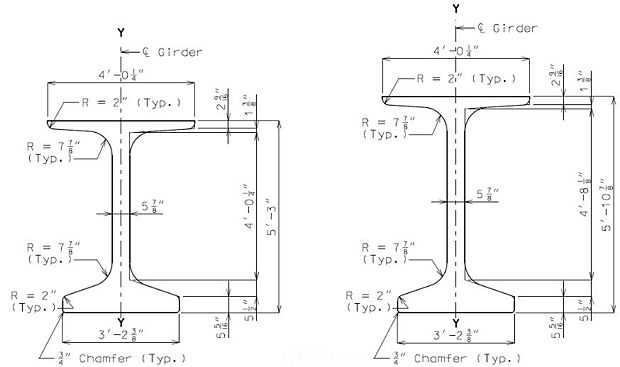
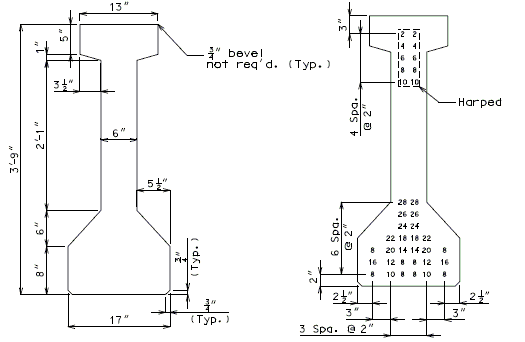
751.22.3.2.4 Beam Type 6 Dimensions/Strand Arrangements
|
|
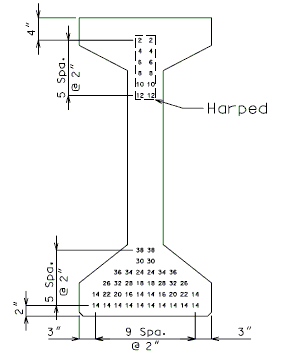 GROUP I |
Numbers shown on girders relate to strand locations. |
ATTENTION: Location of harped strands shown in top flange are at end of girder and harped strands in bottom flange are at centerline.
If the web thickness is required to be increased, then the top and bottom flanges are to be increased by the same amount. (1" increments, 2" max.)
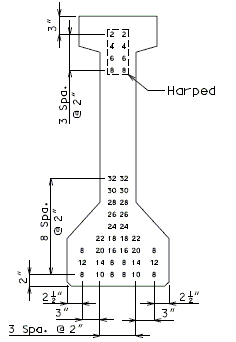
751.22.3.2.5 Beam Type 7 Dimensions/Strand Arrangements
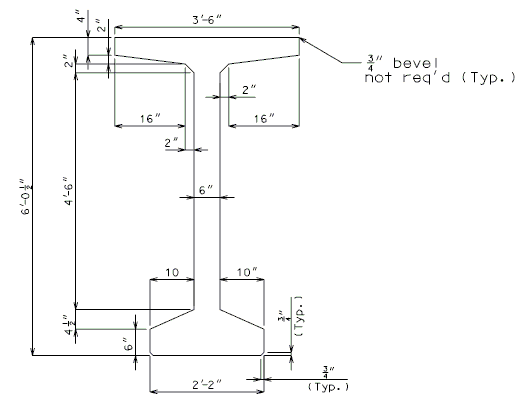
|
|
 GROUP I |
Numbers shown on girders relate to strand locations. |
ATTENTION: Location of harped strands shown in top flange are at end of girder and harped strands in bottom flange are at centerline.
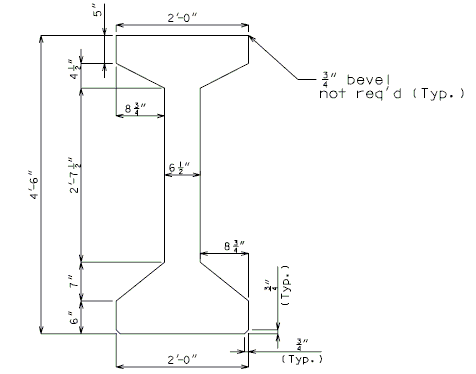
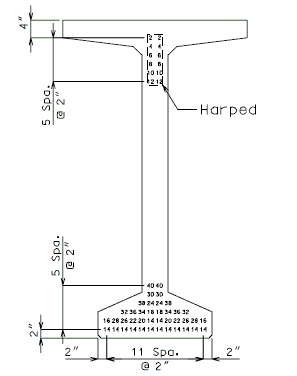
751.22.3.3 NU Standard Girders
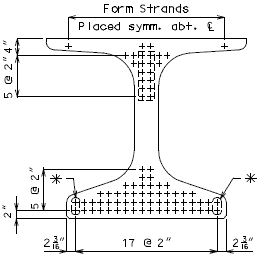
- Note: Strand arrangements shall start at the bottom row and then move up for the most efficient design.
751.22.3.4 Beam Section Properties Tables - Conventional Concrete Strength
The properties of prestressed I-girders in the following tables are valid for = 4.5 ksi and = 6 ksi. The modular ratio , , is 8 for the initial moment of inertia, , and 7 for the final moment of inertia, .
Note: Moments of inertia, and are computed based on transformed non-composite section and are used in camber calculations.
Definitions used in tables are:
| Section Area | = | Gross area of girder, (in.2) |
| Section | = | Distance from bottom of girder to center of gravity of non-transformed non-composite section, (in.) |
| = | Moment of inertia of non-transformed non-composite section, (in.4) | |
| Depth | = | Height of girder, (in.) |
| Strand size | = | Strand diameter, (in.) |
| e1* | = | Eccentricity between centroid of straight strands (CSS) and center of gravity of non-transformed non-composite section (CGB) as shown in figure below, (in.) |
| e2* | = | Eccentricity between centroid of harped strands (CHS) and center of gravity of non-transformed non-composite section (CGB) at midspan as shown in figure below, (in.) |
| e3* | = | Eccentricity between centroid of harped strands (CHS) and center of gravity of non-transformed non-composite section (CGB) at the end of girder as shown in figure below, (in.) |
A more accurate value can be used based on transformed non-composite section. The final camber calculation will not be significantly different using values between transformed and non-transformed sections.
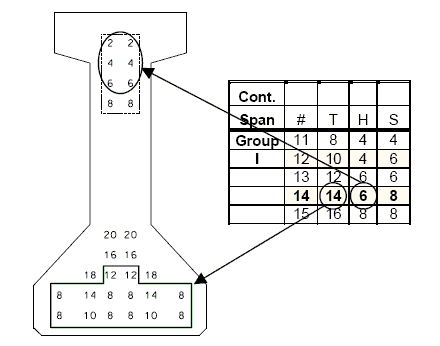
Steps for detailing strand patterns from Prestressed Beam Tables
- For strand locations at mid-span of girder: Look up the "Total Number of Strands" value for the corresponding strand pattern number. The strands will then be located at that number and all numbers below that number. Ex. For 14 total strands, the strands will be placed at all locations numbered ≤14.
- For harped strand locations at end of girder: Look up the "Number of Harped Strands" value for the corresponding strand pattern number. The strands will then be located at that number and all numbers below that number. Ex. For 6 harped strands, the strands will be placed at all locations numbered ≤6.
- GROUP I
Section Properties
Beam Type 2 -- 6" Web
| Section Area = | 310.9 | in2 |
| ||||||||||||||||
| Section = | 14.08 | in | |||||||||||||||||
| = | 33,974 | in4 | |||||||||||||||||
| Depth= | 32 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Iinitial | Ifinal | ||||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars, 2-#6 | |
| Group | 1 | 8 | 4 | 4 | 11.08 | 11.08 | 13.92 | 36,147 | 36,627 | 35,837 | 36,248 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 10 | 4 | 6 | 11.41 | 11.08 | 13.92 | 36,453 | 36,938 | 36,100 | 36,515 |
| 3 | 12 | 6 | 6 | 11.41 | 10.08 | 12.92 | 36,587 | 37,075 | 36,215 | 36,632 | |
| 4 | 14 | 6 | 8 | 11.08 | 10.08 | 12.92 | 36,794 | 37,286 | 36,394 | 36,814 | |
| 5 | 16 | 8 | 8 | 11.08 | 9.08 | 11.92 | 36,866 | 37,360 | 36,456 | 36,878 | |
| 6 | 18 | 8 | 10 | 10.48 | 9.08 | 11.92 | 36,994 | 37,491 | 36,568 | 36,992 | |
| Group | 7 | 8 | 2 | 6 | 11.41 | 10.08 | 14.92 | 36,147 | 36,627 | 35,837 | 36,248 |
| II | 8 | 10 | 2 | 8 | 11.58 | 10.08 | 14.92 | 36,453 | 36,938 | 36,100 | 36,515 |
| 9 | 12 | 4 | 8 | 11.08 | 11.08 | 13.92 | 36,663 | 37,151 | 36,280 | 36,698 | |
| 10 | 14 | 4 | 10 | 11.28 | 9.08 | 13.92 | 36,794 | 37,286 | 36,394 | 36,814 | |
| 11 | 16 | 6 | 10 | 11.28 | 8.08 | 12.92 | 36,866 | 37,360 | 36,456 | 36,878 | |
| 12 | 18 | 6 | 12 | 10.75 | 8.08 | 12.92 | 36,994 | 37,491 | 36,568 | 36,992 | |
| 13 | 20 | 6 | 14 | 10.65 | 6.08 | 12.92 | 37,024 | 37,522 | 36,594 | 37,019 | |
Section Properties
Beam Type 2 -- 7" Web
| Section Area = | 342.9 | in2 |
| ||||||||||||||||
| Section = | 14.26 | in | |||||||||||||||||
| = | 36,812 | in4 | |||||||||||||||||
| Depth= | 32 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Iinitial | Ifinal | ||||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 | |
| Group | 1 | 8 | 4 | 4 | 11.26 | 11.26 | 13.74 | 38,994 | 39,464 | 38,683 | 39,085 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 10 | 4 | 6 | 11.59 | 11.26 | 13.74 | 39,310 | 39,784 | 38,954 | 39,360 |
| 3 | 12 | 6 | 6 | 11.59 | 10.26 | 12.74 | 39,450 | 39,927 | 39,075 | 39,482 | |
| 4 | 14 | 6 | 8 | 11.26 | 10.26 | 12.74 | 39,666 | 40,146 | 39,261 | 39,671 | |
| 5 | 16 | 8 | 8 | 11.26 | 9.26 | 11.74 | 39,742 | 40,225 | 39,327 | 39,739 | |
| 6 | 18 | 8 | 10 | 10.66 | 9.26 | 11.74 | 39,877 | 40,363 | 39,444 | 39,858 | |
| Group | 7 | 8 | 2 | 6 | 11.59 | 10.26 | 14.74 | 38,994 | 39,464 | 38,683 | 39,085 |
| II | 8 | 10 | 2 | 8 | 11.76 | 10.26 | 14.74 | 39,310 | 39,784 | 38,954 | 39,360 |
| 9 | 12 | 4 | 8 | 11.26 | 11.26 | 13.74 | 39,528 | 40,005 | 39,142 | 39,550 | |
| 10 | 14 | 4 | 10 | 11.46 | 9.26 | 13.74 | 39,666 | 40,146 | 39,261 | 39,671 | |
| 11 | 16 | 6 | 10 | 11.46 | 8.26 | 12.74 | 39,742 | 40,225 | 39,327 | 39,739 | |
| 12 | 18 | 6 | 12 | 10.93 | 8.26 | 12.74 | 39,877 | 40,363 | 39,444 | 39,858 | |
| 13 | 20 | 6 | 14 | 10.83 | 6.26 | 12.74 | 39,910 | 39,473 | 39,473 | 39,888 | |
Section Properties
Beam Type 2 -- 8" Web
| Section Area = | 374.9 | in2 |
| ||||||||||||||||
| Section = | 14.41 | in | |||||||||||||||||
| = | 39,632 | in4 | |||||||||||||||||
| Depth= | 32 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Iinitial | Ifinal | ||||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 | |
| Group | 1 | 8 | 4 | 4 | 11.41 | 11.41 | 13.59 | 41,823 | 42,283 | 41,510 | 41,905 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 10 | 4 | 6 | 11.74 | 11.41 | 13.59 | 42,147 | 42,611 | 41,789 | 42,186 |
| 3 | 12 | 6 | 6 | 11.74 | 10.41 | 12.59 | 42,292 | 42,760 | 41,914 | 42,313 | |
| 4 | 14 | 6 | 8 | 11.41 | 10.41 | 12.59 | 42,515 | 42,985 | 42,106 | 42,508 | |
| 5 | 16 | 8 | 8 | 11.41 | 9.41 | 11.59 | 42,596 | 43,068 | 42,176 | 42,579 | |
| 6 | 18 | 8 | 10 | 10.81 | 9.41 | 11.59 | 42,737 | 43,212 | 42,298 | 42,703 | |
| Group | 7 | 8 | 2 | 6 | 11.74 | 10.41 | 14.59 | 41,823 | 42,283 | 41,510 | 41,905 |
| II | 8 | 10 | 2 | 8 | 11.91 | 10.41 | 14.59 | 42,147 | 42,611 | 41,789 | 42,186 |
| 9 | 12 | 4 | 8 | 11.41 | 11.41 | 13.59 | 42,371 | 42,839 | 41,982 | 42,382 | |
| 10 | 14 | 4 | 10 | 11.61 | 9.41 | 13.59 | 42,515 | 42,985 | 42,106 | 42,508 | |
| 11 | 16 | 6 | 10 | 11.61 | 8.41 | 12.59 | 42,596 | 43,068 | 42,176 | 42,579 | |
| 12 | 18 | 6 | 12 | 11.08 | 8.41 | 12.59 | 42,737 | 43,212 | 42,298 | 42,703 | |
| 13 | 20 | 6 | 14 | 10.98 | 6.41 | 12.59 | 42,772 | 43,249 | 42,329 | 42,736 | |
Section Properties
Beam Type 3 -- 6" Web
| Section Area = | 381.9 | in2 |
| ||||||||||||||||
| Section = | 17.08 | in | |||||||||||||||||
| = | 61,841 | in4 | |||||||||||||||||
| Depth= | 39 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 13.08 | 14.08 | 17.92 | 65,179 | 65,930 | 64,702 | 65,346 |
| I | 2 | 10 | 4 | 6 | 13.75 | 14.08 | 17.92 | 65,659 | 66,415 | 65,114 | 65,762 |
| 3 | 12 | 4 | 8 | 13.58 | 14.08 | 17.92 | 66,014 | 66,776 | 65,421 | 66,072 | |
| 4 | 14 | 6 | 8 | 13.58 | 13.08 | 16.92 | 66,265 | 67,032 | 65,637 | 66,292 | |
| 5 | 16 | 6 | 10 | 13.48 | 13.08 | 16.92 | 66,614 | 67,386 | 65,938 | 66,597 | |
| 6 | 18 | 8 | 10 | 13.48 | 12.08 | 15.92 | 66,776 | 67,552 | 66,079 | 66,740 | |
| 7 | 20 | 8 | 12 | 13.08 | 12.08 | 15.92 | 67,020 | 67,799 | 66,290 | 66,954 | |
| 8 | 22 | 8 | 14 | 12.51 | 12.08 | 15.92 | 67,178 | 67,961 | 66,427 | 67,095 | |
| 9 | 24 | 10 | 14 | 12.51 | 11.08 | 14.92 | 67,270 | 68,056 | 66,508 | 67,177 | |
| Group | 10 | 8 | 2 | 6 | 13.75 | 13.08 | 18.92 | 65,179 | 65,930 | 64,702 | 65,346 |
| II | 11 | 10 | 2 | 8 | 14.08 | 13.08 | 18.92 | 65,659 | 66,415 | 65,114 | 65,762 |
| 12 | 12 | 2 | 10 | 13.88 | 13.08 | 18.92 | 66,014 | 66,776 | 65,421 | 66,072 | |
| 13 | 14 | 4 | 10 | 13.48 | 14.08 | 17.92 | 66,366 | 67,134 | 65,724 | 66,379 | |
| 14 | 16 | 4 | 12 | 13.75 | 12.08 | 17.92 | 66,614 | 67,386 | 65,938 | 66,597 | |
| 15 | 18 | 6 | 12 | 13.75 | 11.08 | 16.92 | 66,776 | 67,552 | 66,079 | 66,740 | |
| 16 | 20 | 6 | 14 | 13.37 | 11.08 | 16.92 | 67,020 | 67,799 | 66,290 | 66,954 | |
| 17 | 22 | 6 | 16 | 12.83 | 11.08 | 16.92 | 67,178 | 67,961 | 66,427 | 67,095 | |
| 18 | 24 | 8 | 16 | 12.83 | 10.08 | 15.92 | 67,270 | 68,056 | 66,508 | 67,177 | |
Section Properties
Beam Type 3 -- 7" Web
| Section Area = | 420.9 | in2 |
| ||||||||||||||||
| Section = | 17.31 | in | |||||||||||||||||
| = | 66,991 | in4 | |||||||||||||||||
| Depth= | 39 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 13.31 | 14.31 | 17.69 | 70,343 | 71,077 | 69,865 | 70,493 |
| I | 2 | 10 | 4 | 6 | 13.98 | 14.31 | 17.69 | 70,838 | 71,577 | 70,289 | 70,922 |
| 3 | 12 | 4 | 8 | 13.81 | 14.31 | 17.69 | 71,207 | 71,951 | 70,607 | 71,243 | |
| 4 | 14 | 6 | 8 | 13.81 | 13.31 | 16.69 | 71,469 | 72,218 | 70,833 | 71,473 | |
| 5 | 16 | 6 | 10 | 13.71 | 13.31 | 16.69 | 71,832 | 72,585 | 71,146 | 71,789 | |
| 6 | 18 | 8 | 10 | 13.71 | 12.31 | 15.69 | 72,004 | 72,760 | 71,295 | 71,940 | |
| 7 | 20 | 8 | 12 | 13.31 | 12.31 | 15.69 | 72,259 | 73,019 | 71,516 | 72,164 | |
| 8 | 22 | 8 | 14 | 12.74 | 12.31 | 15.69 | 72,427 | 73,190 | 71,662 | 72,312 | |
| 9 | 24 | 10 | 14 | 12.74 | 11.31 | 14.69 | 72,526 | 73,292 | 71,749 | 72,401 | |
| Group | 10 | 8 | 2 | 6 | 13.98 | 13.31 | 18.69 | 70,343 | 71,077 | 69,865 | 70,493 |
| II | 11 | 10 | 2 | 8 | 14.31 | 13.31 | 18.69 | 70,838 | 71,577 | 70,289 | 70,922 |
| 12 | 12 | 2 | 10 | 14.11 | 13.31 | 18.69 | 71,207 | 71,951 | 70,607 | 71,243 | |
| 13 | 14 | 4 | 10 | 13.71 | 14.31 | 17.69 | 71,572 | 72,322 | 70,922 | 71,562 | |
| 14 | 16 | 4 | 12 | 13.98 | 12.31 | 17.69 | 71,832 | 72,585 | 71,146 | 71,789 | |
| 15 | 18 | 6 | 12 | 13.98 | 11.31 | 16.69 | 72,004 | 72,760 | 71,295 | 71,940 | |
| 16 | 20 | 6 | 14 | 13.60 | 11.31 | 16.69 | 72,259 | 73,019 | 71,516 | 72,164 | |
| 17 | 22 | 6 | 16 | 13.06 | 11.31 | 16.69 | 72,427 | 73,190 | 71,662 | 72,312 | |
| 18 | 24 | 8 | 16 | 13.06 | 10.31 | 15.69 | 72,526 | 73,292 | 71,749 | 72,401 | |
Section Properties
Beam Type 3 -- 8" Web
| Section Area = | 459.9 | in2 |
| ||||||||||||||||
| Section = | 17.49 | in | |||||||||||||||||
| = | 72,106 | in4 | |||||||||||||||||
| Depth= | 39 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 13.49 | 14.49 | 17.51 | 75,470 | 76,191 | 74,990 | 75,607 |
| I | 2 | 10 | 4 | 6 | 14.16 | 14.49 | 17.51 | 75,977 | 76,703 | 75,425 | 76,046 |
| 3 | 12 | 4 | 8 | 13.99 | 14.49 | 17.51 | 76,357 | 77,087 | 75,752 | 76,376 | |
| 4 | 14 | 6 | 8 | 13.99 | 13.49 | 16.51 | 76,628 | 77,363 | 75,986 | 76,613 | |
| 5 | 16 | 6 | 10 | 13.89 | 13.49 | 16.51 | 77,002 | 77,740 | 76,308 | 76,939 | |
| 6 | 18 | 8 | 10 | 13.89 | 12.49 | 15.51 | 77,182 | 77,923 | 76,464 | 77,096 | |
| 7 | 20 | 8 | 12 | 13.49 | 12.49 | 15.51 | 77,446 | 78,191 | 76,692 | 77,328 | |
| 8 | 22 | 8 | 14 | 12.92 | 12.49 | 15.51 | 77,622 | 78,370 | 76,845 | 77,483 | |
| 9 | 24 | 10 | 14 | 12.92 | 11.49 | 14.51 | 77,728 | 78,479 | 76,938 | 77,577 | |
| Group | 10 | 8 | 2 | 6 | 14.16 | 13.49 | 18.51 | 75,470 | 76,191 | 74,990 | 75,607 |
| II | 11 | 10 | 2 | 8 | 14.49 | 13.49 | 18.51 | 75,977 | 76,703 | 75,425 | 76,046 |
| 12 | 12 | 2 | 10 | 14.29 | 13.49 | 18.51 | 76,357 | 77,087 | 75,752 | 76,376 | |
| 13 | 14 | 4 | 10 | 13.89 | 14.49 | 17.51 | 76,733 | 77,468 | 76,076 | 76,704 | |
| 14 | 16 | 4 | 12 | 14.16 | 12.49 | 17.51 | 77,002 | 77,740 | 76,308 | 76,939 | |
| 15 | 18 | 6 | 12 | 14.16 | 11.49 | 16.51 | 77,182 | 77,923 | 76,464 | 77,096 | |
| 16 | 20 | 6 | 14 | 13.78 | 11.49 | 16.51 | 77,446 | 78,191 | 76,692 | 77,328 | |
| 17 | 22 | 6 | 16 | 13.24 | 11.49 | 16.51 | 77,622 | 78,370 | 76,845 | 77,483 | |
| 18 | 24 | 8 | 16 | 13.24 | 10.49 | 15.51 | 77,728 | 78,479 | 76,938 | 77,577 | |
Section Properties
Beam Type 4 -- 6" Web
| Section Area = | 428.9 | in2 |
| ||||||||||||||||
| Section = | 19.54 | in | |||||||||||||||||
| = | 92,450 | in4 | |||||||||||||||||
| Depth= | 45 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 15.54 | 16.54 | 21.46 | 97,077 | 98,118 | 96,416 | 97,308 |
| I | 2 | 10 | 4 | 6 | 16.21 | 16.54 | 21.46 | 97,727 | 98,775 | 96,974 | 97,872 |
| 3 | 12 | 4 | 8 | 16.04 | 16.54 | 21.46 | 98,231 | 99,286 | 97,408 | 98,310 | |
| 4 | 14 | 6 | 8 | 16.04 | 15.54 | 20.46 | 98,608 | 99,669 | 97,733 | 98,640 | |
| 5 | 16 | 6 | 10 | 15.94 | 15.54 | 20.46 | 99,103 | 100,170 | 98,160 | 99,071 | |
| 6 | 18 | 8 | 10 | 15.94 | 14.54 | 19.46 | 99,368 | 100,441 | 98,390 | 99,305 | |
| 7 | 20 | 8 | 12 | 15.54 | 14.54 | 19.46 | 99,735 | 100,813 | 98,707 | 99,626 | |
| 8 | 22 | 8 | 14 | 14.97 | 14.54 | 19.46 | 99,995 | 101,078 | 98,933 | 99,856 | |
| 9 | 24 | 8 | 16 | 15.29 | 12.54 | 19.46 | 100,168 | 101,254 | 99,083 | 100,009 | |
| 10 | 26 | 10 | 16 | 15.29 | 11.54 | 18.46 | 100,271 | 101,360 | 99,174 | 100,102 | |
| 11 | 28 | 10 | 18 | 15.32 | 9.54 | 18.46 | 100,323 | 101,414 | 99,220 | 100,149 | |
| Group | 12 | 8 | 2 | 6 | 16.21 | 15.54 | 22.46 | 97,077 | 98,118 | 96,416 | 97,308 |
| II | 13 | 10 | 2 | 8 | 16.54 | 15.54 | 22.46 | 97,727 | 98,775 | 96,974 | 97,872 |
| 14 | 12 | 4 | 8 | 16.04 | 16.54 | 21.46 | 98,231 | 99,286 | 97,408 | 98,310 | |
| 15 | 14 | 4 | 10 | 15.94 | 16.54 | 21.46 | 98,730 | 99,792 | 97,838 | 98,745 | |
| 16 | 16 | 4 | 12 | 16.21 | 14.54 | 21.46 | 99,103 | 100,170 | 98,160 | 99,071 | |
| 17 | 16 | 6 | 10 | 15.94 | 15.54 | 20.46 | 99,103 | 100,170 | 98,160 | 99,071 | |
| 18 | 18 | 6 | 12 | 16.21 | 13.54 | 20.46 | 99,368 | 100,441 | 98,390 | 99,305 | |
| 19 | 20 | 6 | 14 | 15.83 | 13.54 | 20.46 | 99,735 | 100,813 | 98,707 | 99,626 | |
| 20 | 22 | 6 | 16 | 15.29 | 13.54 | 20.46 | 99,995 | 101,078 | 98,933 | 99,856 | |
| 21 | 24 | 6 | 18 | 15.32 | 11.54 | 20.46 | 100,168 | 101,254 | 99,083 | 100,009 | |
| 22 | 26 | 6 | 20 | 15.14 | 9.54 | 20.46 | 100,271 | 101,360 | 99,174 | 100,102 | |
| 23 | 26 | 8 | 18 | 15.32 | 10.54 | 19.46 | 100,271 | 101,360 | 99,174 | 100,102 | |
| 24 | 28 | 6 | 22 | 14.81 | 7.54 | 20.46 | 100,323 | 101,414 | 99,220 | 100,149 | |
| 25 | 28 | 8 | 20 | 15.14 | 8.54 | 19.46 | 100,323 | 101,414 | 99,220 | 100,149 | |
| 26 | 30 | 8 | 22 | 14.81 | 6.54 | 19.46 | 100,341 | 101,433 | 99,236 | 100,166 | |
| 27 | 32 | 8 | 24 | 14.37 | 4.54 | 19.46 | 100,342 | 101,435 | 99,238 | 100,168 | |
Section Properties
Beam Type 4 -- 7" Web
| Section Area = | 473.9 | in2 |
| ||||||||||||||||
| Section = | 19.82 | in | |||||||||||||||||
| = | 100,400 | in4 | |||||||||||||||||
| Depth= | 45 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 15.82 | 16.82 | 21.18 | 105,048 | 106,065 | 104,384 | 105,256 |
| I | 2 | 10 | 4 | 6 | 16.49 | 16.82 | 21.18 | 105,719 | 106,743 | 104,960 | 105,837 |
| 3 | 12 | 4 | 8 | 16.32 | 16.82 | 21.18 | 106,242 | 107,272 | 105,410 | 106,291 | |
| 4 | 14 | 6 | 8 | 16.32 | 15.82 | 20.18 | 106,636 | 107,671 | 105,750 | 106,635 | |
| 5 | 16 | 6 | 10 | 16.22 | 15.82 | 20.18 | 107,151 | 108,192 | 106,193 | 107,083 | |
| 6 | 18 | 8 | 10 | 16.22 | 14.82 | 19.18 | 107,431 | 108,476 | 106,436 | 107,328 | |
| 7 | 20 | 8 | 12 | 15.82 | 14.82 | 19.18 | 107,815 | 108,866 | 106,768 | 107,664 | |
| 8 | 22 | 8 | 14 | 15.25 | 14.82 | 19.18 | 108,090 | 109,145 | 107,007 | 107,906 | |
| 9 | 24 | 8 | 16 | 15.57 | 12.82 | 19.18 | 108,275 | 109,334 | 107,168 | 108,070 | |
| 10 | 26 | 10 | 16 | 15.57 | 11.82 | 18.18 | 108,388 | 109,449 | 107,266 | 108,171 | |
| 11 | 28 | 10 | 18 | 15.60 | 9.82 | 18.18 | 108,446 | 109,510 | 107,318 | 108,224 | |
| Group | 12 | 8 | 2 | 6 | 16.49 | 15.82 | 22.18 | 105,048 | 106,065 | 104,384 | 105,256 |
| II | 13 | 10 | 2 | 8 | 16.82 | 15.82 | 22.18 | 105,719 | 106,743 | 104,960 | 105,837 |
| 14 | 12 | 4 | 8 | 16.32 | 16.82 | 21.18 | 106,242 | 107,272 | 105,410 | 106,291 | |
| 15 | 14 | 4 | 10 | 16.22 | 16.82 | 21.18 | 106,760 | 107,796 | 105,857 | 106,742 | |
| 16 | 16 | 4 | 12 | 16.49 | 14.82 | 21.18 | 107,151 | 108,192 | 106,193 | 107,083 | |
| 17 | 16 | 6 | 10 | 16.22 | 15.82 | 20.18 | 107,151 | 108,192 | 106,193 | 107,083 | |
| 18 | 18 | 6 | 12 | 16.49 | 13.82 | 20.18 | 107,431 | 108,476 | 106,436 | 107,328 | |
| 19 | 20 | 6 | 14 | 16.11 | 13.82 | 20.18 | 107,815 | 108,866 | 106,768 | 107,664 | |
| 20 | 22 | 6 | 16 | 15.57 | 13.82 | 20.18 | 108,090 | 109,145 | 107,007 | 107,906 | |
| 21 | 24 | 6 | 18 | 15.60 | 11.82 | 20.18 | 108,275 | 109,334 | 107,168 | 108,070 | |
| 22 | 26 | 6 | 20 | 15.42 | 9.82 | 20.18 | 108,388 | 109,449 | 107,266 | 108,171 | |
| 23 | 26 | 8 | 18 | 15.60 | 10.82 | 19.18 | 108,388 | 109,449 | 107,266 | 108,171 | |
| 24 | 28 | 6 | 22 | 15.09 | 7.82 | 20.18 | 108,446 | 109,510 | 107,318 | 108,224 | |
| 25 | 28 | 8 | 20 | 15.42 | 8.82 | 19.18 | 108,446 | 109,510 | 107,318 | 108,224 | |
| 26 | 30 | 8 | 22 | 15.09 | 6.82 | 19.18 | 108,469 | 109,533 | 107,338 | 108,245 | |
| 27 | 32 | 8 | 24 | 14.65 | 4.82 | 19.18 | 108,472 | 109,537 | 107,341 | 108,248 | |
Section Properties
Beam Type 4 -- 8" Web
| Section Area = | 518.9 | in2 |
| ||||||||||||||||
| Section = | 20.06 | in | |||||||||||||||||
| = | 108,288 | in4 | |||||||||||||||||
| Depth= | 45 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 16.06 | 17.06 | 20.94 | 112,955 | 113,952 | 112,289 | 113,143 |
| I | 2 | 10 | 4 | 6 | 16.73 | 17.06 | 20.94 | 113,645 | 114,648 | 112,881 | 113,739 |
| 3 | 12 | 4 | 8 | 16.56 | 17.06 | 20.94 | 114,185 | 115,193 | 113,345 | 114,208 | |
| 4 | 14 | 6 | 8 | 16.56 | 16.06 | 19.94 | 114,594 | 115,607 | 113,698 | 114,563 | |
| 5 | 16 | 6 | 10 | 16.46 | 16.06 | 19.94 | 115,126 | 116,144 | 114,156 | 115,026 | |
| 6 | 18 | 8 | 10 | 16.46 | 15.06 | 18.94 | 115,419 | 116,442 | 114,409 | 115,282 | |
| 7 | 20 | 8 | 12 | 16.06 | 15.06 | 18.94 | 115,818 | 116,846 | 114,755 | 115,631 | |
| 8 | 22 | 8 | 14 | 15.49 | 15.06 | 18.94 | 116,107 | 117,138 | 115,004 | 115,884 | |
| 9 | 24 | 8 | 16 | 15.81 | 13.06 | 18.94 | 116,303 | 117,337 | 115,175 | 116,057 | |
| 10 | 26 | 10 | 16 | 15.81 | 12.06 | 17.94 | 116,424 | 117,461 | 115,281 | 116,165 | |
| 11 | 28 | 10 | 18 | 15.84 | 10.06 | 17.94 | 116,489 | 117,528 | 115,338 | 116,223 | |
| Group | 12 | 8 | 2 | 6 | 16.73 | 16.06 | 21.94 | 112,955 | 113,952 | 112,289 | 113,143 |
| II | 13 | 10 | 2 | 8 | 17.06 | 16.06 | 21.94 | 113,645 | 114,648 | 112,881 | 113,739 |
| 14 | 12 | 4 | 8 | 16.56 | 17.06 | 20.94 | 114,185 | 115,193 | 113,345 | 114,208 | |
| 15 | 14 | 4 | 10 | 16.46 | 17.06 | 20.94 | 114,720 | 115,734 | 113,806 | 114,673 | |
| 16 | 16 | 4 | 12 | 16.73 | 15.06 | 20.94 | 115,126 | 116,144 | 114,156 | 115,026 | |
| 17 | 16 | 6 | 10 | 16.46 | 16.06 | 19.94 | 115,126 | 116,144 | 114,156 | 115,026 | |
| 18 | 18 | 6 | 12 | 16.73 | 14.06 | 19.94 | 115,419 | 116,442 | 114,409 | 115,282 | |
| 19 | 20 | 6 | 14 | 16.35 | 14.06 | 19.94 | 115,818 | 116,846 | 114,755 | 115,631 | |
| 20 | 22 | 6 | 16 | 15.81 | 14.06 | 19.94 | 116,107 | 117,138 | 115,004 | 115,884 | |
| 21 | 24 | 6 | 18 | 15.84 | 12.06 | 19.94 | 116,303 | 117,337 | 115,175 | 116,057 | |
| 22 | 26 | 6 | 20 | 15.66 | 10.06 | 19.94 | 116,424 | 117,461 | 115,281 | 116,165 | |
| 23 | 26 | 8 | 18 | 15.84 | 11.06 | 18.94 | 116,424 | 117,461 | 115,281 | 116,165 | |
| 24 | 28 | 6 | 22 | 15.33 | 8.06 | 19.94 | 116,489 | 117,528 | 115,338 | 116,223 | |
| 25 | 28 | 8 | 20 | 15.66 | 9.06 | 18.94 | 116,489 | 117,528 | 115,338 | 116,223 | |
| 26 | 30 | 8 | 22 | 15.33 | 7.06 | 18.94 | 116,515 | 117,555 | 115,361 | 116,247 | |
| 27 | 32 | 8 | 24 | 14.89 | 5.06 | 18.94 | 116,520 | 117,560 | 115,366 | 116,252 | |
Section Properties
Beam Type 6 -- 6.5" Web
| Section Area = | 643.6 | in2 |
| ||||||||||||||||
| Section = | 25.92 | in | |||||||||||||||||
| = | 235,735 | in4 | |||||||||||||||||
| Depth= | 54 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Iinitial | Ifinal | ||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#6 |
A1 Bars 2-#6 | |
| Group | 1 | 14 | 4 | 10 | 23.52 | 22.92 | 23.08 | 248,115 | 246,353 |
|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 16 | 4 | 12 | 23.25 | 22.92 | 23.08 | 249,115 | 247,213 |
| 3 | 18 | 6 | 12 | 23.25 | 21.92 | 22.08 | 249,933 | 247,918 | |
| 4 | 20 | 6 | 14 | 23.06 | 21.92 | 22.08 | 250,920 | 248,769 | |
| 5 | 22 | 6 | 16 | 22.92 | 21.92 | 22.08 | 251,901 | 249,616 | |
| 6 | 24 | 8 | 16 | 22.92 | 20.92 | 21.08 | 252,545 | 250,173 | |
| 7 | 26 | 8 | 18 | 22.59 | 20.92 | 21.08 | 253,342 | 250,862 | |
| 8 | 28 | 8 | 20 | 22.32 | 20.92 | 21.08 | 254,133 | 251,547 | |
| 9 | 30 | 10 | 20 | 22.32 | 19.92 | 20.08 | 254,626 | 251,975 | |
| 10 | 32 | 10 | 22 | 22.10 | 19.92 | 20.08 | 255,408 | 252,653 | |
| 11 | 34 | 10 | 24 | 21.75 | 19.92 | 20.08 | 256,032 | 253,195 | |
| 12 | 36 | 10 | 26 | 21.46 | 19.92 | 20.08 | 256,651 | 253,734 | |
| 13 | 38 | 12 | 26 | 21.46 | 18.92 | 19.08 | 257,011 | 254,048 |
Section Properties
Beam Type 6 -- 7.5" Web
| Section Area = | 697.6 | in2 |
| ||||||||||||||||
| Section = | 26.00 | in | |||||||||||||||||
| = | 248,915 | in4 | |||||||||||||||||
| Depth= | 54 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Iinitial | Ifinal | ||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#6 |
A1 Bars 2-#6 | |
| Group | 1 | 14 | 4 | 10 | 23.60 | 23.00 | 23.00 | 262,852 | 260,864 |
|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 16 | 4 | 12 | 23.33 | 23.00 | 23.00 | 263,868 | 261,737 |
| 3 | 18 | 6 | 12 | 23.33 | 22.00 | 22.00 | 264,701 | 262,454 | |
| 4 | 20 | 6 | 14 | 23.14 | 22.00 | 22.00 | 265,707 | 263,319 | |
| 5 | 22 | 6 | 16 | 23.00 | 22.00 | 22.00 | 266,706 | 264,180 | |
| 6 | 24 | 8 | 16 | 23.00 | 21.00 | 21.00 | 267,365 | 264,749 | |
| 7 | 26 | 8 | 18 | 22.67 | 21.00 | 21.00 | 268,178 | 265,452 | |
| 8 | 28 | 8 | 20 | 22.40 | 21.00 | 21.00 | 268,987 | 266,150 | |
| 9 | 30 | 10 | 20 | 22.40 | 20.00 | 20.00 | 269,493 | 266,589 | |
| 10 | 32 | 10 | 22 | 22.18 | 20.00 | 20.00 | 270,294 | 267,282 | |
| 11 | 34 | 10 | 24 | 21.83 | 20.00 | 20.00 | 270,933 | 267,836 | |
| 12 | 36 | 10 | 26 | 21.54 | 20.00 | 20.00 | 271,569 | 268,387 | |
| 13 | 38 | 12 | 26 | 21.54 | 19.00 | 19.00 | 271,941 | 268,712 |
Section Properties
Beam Type 6 -- 8.5" Web
| Section Area = | 751.6 | in2 |
| ||||||||||||||||
| Section = | 26.07 | in | |||||||||||||||||
| = | 262,087 | in4 | |||||||||||||||||
| Depth= | 54 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Iinitial | Ifinal | ||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#6 |
A1 Bars 2-#6 | |
| Group | 1 | 14 | 4 | 10 | 23.67 | 23.07 | 22.93 | 276,043 | 274,052 |
|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 16 | 4 | 12 | 23.40 | 23.07 | 22.93 | 277,068 | 274,932 |
| 3 | 18 | 6 | 12 | 23.40 | 22.07 | 21.93 | 277,908 | 275,656 | |
| 4 | 20 | 6 | 14 | 23.21 | 22.07 | 21.93 | 278,922 | 276,528 | |
| 5 | 22 | 6 | 16 | 23.07 | 22.07 | 21.93 | 279,930 | 277,396 | |
| 6 | 24 | 8 | 16 | 23.07 | 21.07 | 20.93 | 280,596 | 277,971 | |
| 7 | 26 | 8 | 18 | 22.74 | 21.07 | 20.93 | 281,418 | 278,680 | |
| 8 | 28 | 8 | 20 | 22.47 | 21.07 | 20.93 | 282,236 | 279,386 | |
| 9 | 30 | 10 | 20 | 22.47 | 20.07 | 19.93 | 282,750 | 279,831 | |
| 10 | 32 | 10 | 22 | 22.25 | 20.07 | 19.93 | 283,559 | 280,531 | |
| 11 | 34 | 10 | 24 | 21.90 | 20.07 | 19.93 | 284,207 | 281,093 | |
| 12 | 36 | 10 | 26 | 21.61 | 20.07 | 19.93 | 284,851 | 281,651 | |
| 13 | 38 | 12 | 26 | 21.61 | 19.07 | 18.93 | 285,230 | 281,981 |
Section Properties
Beam Type 7 -- 6" Web
Bulb Tee Girder
| Section Area = | 787.4 | in2 |
| ||||||||||||||||
| Section = | 37.58 | in | |||||||||||||||||
| = | 571,047 | in4 | |||||||||||||||||
| Depth= | 72.5 | in | |||||||||||||||||
| Strand Size= | ½ | in | |||||||||||||||||
| = | 4.5 | ksi | |||||||||||||||||
| = | 6 | ksi |
| Cont. | Iinitial | Ifinal | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 4-#6 |
A1 Bars 4-#6 |
| Group | 1 | 14 | 4 | 10 | 35.58 | 34.58 | 29.92 | 603,636 | 598,983 |
| I | 2 | 16 | 4 | 12 | 35.25 | 34.58 | 29.92 | 606,025 | 601,033 |
| 3 | 18 | 6 | 12 | 35.25 | 33.58 | 28.92 | 608,125 | 602,838 | |
| 4 | 20 | 6 | 14 | 35.01 | 33.58 | 28.92 | 610,490 | 604,871 | |
| 5 | 22 | 6 | 16 | 34.83 | 33.58 | 28.92 | 612,843 | 606,895 | |
| 6 | 24 | 8 | 16 | 34.83 | 32.58 | 27.92 | 614,652 | 608,453 | |
| 7 | 26 | 8 | 18 | 34.69 | 32.58 | 27.92 | 616,981 | 610,459 | |
| 8 | 28 | 8 | 20 | 34.58 | 32.58 | 27.92 | 619,299 | 612,457 | |
| 9 | 30 | 10 | 20 | 34.58 | 31.58 | 26.92 | 620,839 | 613,788 | |
| 10 | 32 | 10 | 22 | 34.31 | 31.58 | 26.92 | 622,864 | 615,536 | |
| 11 | 34 | 10 | 24 | 34.08 | 31.58 | 26.92 | 624,878 | 617,276 | |
| 12 | 36 | 10 | 26 | 33.89 | 31.58 | 26.92 | 626,881 | 619,009 | |
| 13 | 38 | 10 | 28 | 33.58 | 31.58 | 26.92 | 628,622 | 620,517 | |
| 14 | 40 | 12 | 28 | 33.58 | 30.58 | 25.92 | 629,902 | 621,627 |
751.22.3.5 Beam Section Properties Tables - Higher Concrete Strength
The properties of prestressed I-girders in the following tables are valid for = 5 ksi and = 7 ksi. The modular ratio , , is 7 for the initial moment of inertia, , and 6 for the final moment of inertia, .
Note: Moments of inertia, and are computed based on transformed non-composite section and are used in camber calculations. A1 Bar locations are assumed at 3" from the top of girder.
Definitions used in tables are:
| Section Area | = | Gross area of girder, (in.2) |
| Section | = | Distance from bottom of girder to center of gravity of non-transformed non-composite section, (in.) |
| = | Moment of inertia of non-transformed non-composite section, (in.4) | |
| Depth | = | Height of girder, (in.) |
| Strand size | = | Strand diameter, (in.) |
| e1* | = | Eccentricity between centroid of straight strands (CSS) and center of gravity of non-transformed non-composite section (CGB) as shown in figure below, (in.) |
| e2* | = | Eccentricity between centroid of harped strands (CHS) and center of gravity of non-transformed non-composite section (CGB) at midspan as shown in figure below, (in.) |
| e3* | = | Eccentricity between centroid of harped strands (CHS) and center of gravity of non-transformed non-composite section (CGB) at the end of girder as shown in figure below, (in.) |
A more accurate value can be used based on transformed non-composite section. The final camber calculation will not be significantly different using values between transformed and non-transformed sections.

Steps for detailing strand patterns from Prestressed Beam Tables
- For strand locations at mid-span of girder: Look up the "Total Number of Strands" value for the corresponding strand pattern number. The strands will then be located at that number and all numbers below that number. Ex. For 14 total strands, the strands will be placed at all locations numbered ≤14.
- For harped strand locations at end of girder: Look up the "Number of Harped Strands" value for the corresponding strand pattern number. The strands will then be located at that number and all numbers below that number. Ex. For 6 harped strands, the strands will be placed at all locations numbered ≤6.

- GROUP I
Section Properties
Beam Type 2 -- 6" Web
| Section Area = | 310.9 | in2 |
| ||||||||||||||||
| Section = | 14.08 | in | |||||||||||||||||
| = | 33,974 | in4 | |||||||||||||||||
| Depth= | 32 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Iinitial | Ifinal | ||||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars, 2-#6 | |
| Group | 1 | 8 | 4 | 4 | 11.08 | 11.08 | 13.92 | 36,407 | 36,838 | 36,062 | 36,429 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 10 | 4 | 6 | 11.41 | 11.08 | 13.92 | 36,828 | 37,265 | 36,424 | 36,797 |
| 3 | 12 | 6 | 6 | 11.41 | 10.08 | 12.92 | 36,983 | 37,424 | 36,559 | 36,935 | |
| 4 | 14 | 6 | 8 | 11.08 | 10.08 | 12.92 | 37,265 | 37,711 | 36,804 | 37,183 | |
| 5 | 16 | 8 | 8 | 11.08 | 9.08 | 11.92 | 37,304 | 37,753 | 36,839 | 37,221 | |
| 6 | 18 | 8 | 10 | 10.48 | 9.08 | 11.92 | 37,465 | 37,917 | 36,980 | 37,364 | |
| Group | 7 | 8 | 2 | 6 | 11.41 | 10.08 | 14.92 | 36,407 | 36,837 | 36,061 | 36,429 |
| II | 8 | 10 | 2 | 8 | 11.58 | 10.08 | 14.92 | 36,829 | 37,265 | 36,425 | 36,797 |
| 9 | 12 | 4 | 8 | 11.08 | 11.08 | 13.92 | 37,112 | 37,553 | 36,670 | 37,046 | |
| 10 | 14 | 4 | 10 | 11.28 | 9.08 | 13.92 | 37,265 | 37,711 | 36,804 | 37,183 | |
| 11 | 16 | 6 | 10 | 11.28 | 8.08 | 12.92 | 37,304 | 37,753 | 36,839 | 37,221 | |
| 12 | 18 | 6 | 12 | 10.75 | 8.08 | 12.92 | 37,466 | 37,918 | 36,981 | 37,365 | |
| 13 | 20 | 6 | 14 | 10.65 | 6.08 | 12.92 | 37,409 | 37,864 | 36,934 | 37,320 | |
Section Properties
Beam Type 2 -- 7" Web
| Section Area = | 342.9 | in2 |
| ||||||||||||||||
| Section = | 14.26 | in | |||||||||||||||||
| = | 36,812 | in4 | |||||||||||||||||
| Depth= | 32 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Iinitial | Ifinal | ||||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 | |
| Group | 1 | 8 | 4 | 4 | 11.26 | 11.26 | 13.74 | 39,272 | 39,691 | 38,922 | 39,281 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 10 | 4 | 6 | 11.59 | 11.26 | 13.74 | 39,706 | 40,132 | 39,297 | 39,660 |
| 3 | 12 | 6 | 6 | 11.59 | 10.26 | 12.74 | 39,871 | 40,300 | 39,440 | 39,806 | |
| 4 | 14 | 6 | 8 | 11.26 | 10.26 | 12.74 | 40,165 | 40,599 | 39,695 | 40,064 | |
| 5 | 16 | 8 | 8 | 11.26 | 9.26 | 11.74 | 40,211 | 40,648 | 39,736 | 40,108 | |
| 6 | 18 | 8 | 10 | 10.66 | 9.26 | 11.74 | 40,382 | 40,822 | 39,885 | 40,259 | |
| Group | 7 | 8 | 2 | 6 | 11.59 | 10.26 | 14.74 | 39,271 | 39,691 | 38,921 | 39,280 |
| II | 8 | 10 | 2 | 8 | 11.76 | 10.26 | 14.74 | 39,707 | 40,133 | 39,297 | 39,660 |
| 9 | 12 | 4 | 8 | 11.26 | 11.26 | 13.74 | 40,002 | 40,432 | 39,553 | 39,919 | |
| 10 | 14 | 4 | 10 | 11.46 | 9.26 | 13.74 | 40,165 | 40,599 | 39,695 | 40,064 | |
| 11 | 16 | 6 | 10 | 11.46 | 8.26 | 12.74 | 40,211 | 40,648 | 39,736 | 40,108 | |
| 12 | 18 | 6 | 12 | 10.93 | 8.26 | 12.74 | 40,383 | 40,823 | 39,886 | 40,260 | |
| 13 | 20 | 6 | 14 | 10.83 | 6.26 | 12.74 | 40,331 | 40,773 | 39,843 | 40,219 | |
Section Properties
Beam Type 2 -- 8" Web
| Section Area = | 374.9 | in2 |
| ||||||||||||||||
| Section = | 14.41 | in | |||||||||||||||||
| = | 39,632 | in4 | |||||||||||||||||
| Depth= | 32 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Iinitial | Ifinal | ||||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 | |
| Group | 1 | 8 | 4 | 4 | 11.41 | 11.41 | 13.59 | 42,114 | 42,525 | 41,761 | 42,113 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 10 | 4 | 6 | 11.74 | 11.41 | 13.59 | 42,561 | 42,977 | 42,146 | 42,502 |
| 3 | 12 | 6 | 6 | 11.74 | 10.41 | 12.59 | 42,734 | 43,154 | 42,296 | 42,654 | |
| 4 | 14 | 6 | 8 | 11.41 | 10.41 | 12.59 | 43,039 | 43,463 | 42,560 | 42,921 | |
| 5 | 16 | 8 | 8 | 11.41 | 9.41 | 11.59 | 43,091 | 43,518 | 42,607 | 42,970 | |
| 6 | 18 | 8 | 10 | 10.81 | 9.41 | 11.59 | 43,270 | 43,700 | 42,764 | 43,129 | |
| Group | 7 | 8 | 2 | 6 | 11.74 | 10.41 | 14.59 | 42,114 | 42,525 | 41,761 | 42,112 |
| II | 8 | 10 | 2 | 8 | 11.91 | 10.41 | 14.59 | 42,562 | 42,978 | 42,147 | 42,502 |
| 9 | 12 | 4 | 8 | 11.41 | 11.41 | 13.59 | 42,867 | 43,288 | 42,411 | 42,769 | |
| 10 | 14 | 4 | 10 | 11.61 | 9.41 | 13.59 | 43,039 | 43,463 | 42,560 | 42,921 | |
| 11 | 16 | 6 | 10 | 11.61 | 8.41 | 12.59 | 43,091 | 43,518 | 42,607 | 42,970 | |
| 12 | 18 | 6 | 12 | 11.08 | 8.41 | 12.59 | 43,271 | 43,701 | 42,765 | 43,130 | |
| 13 | 20 | 6 | 14 | 10.98 | 6.41 | 12.59 | 43,224 | 43,655 | 42,725 | 43,092 | |
Section Properties
Beam Type 3 -- 6" Web
| Section Area = | 381.9 | in2 |
| ||||||||||||||||
| Section = | 17.08 | in | |||||||||||||||||
| = | 61,841 | in4 | |||||||||||||||||
| Depth= | 39 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 13.08 | 14.08 | 17.92 | 65,603 | 66,291 | 65,068 | 65,656 |
| I | 2 | 10 | 4 | 6 | 13.75 | 14.08 | 17.92 | 66,265 | 66,962 | 65,638 | 66,233 |
| 3 | 12 | 4 | 8 | 13.58 | 14.08 | 17.92 | 66,753 | 67,457 | 66,060 | 66,660 | |
| 4 | 14 | 6 | 8 | 13.58 | 13.08 | 16.92 | 67,077 | 67,787 | 66,341 | 66,945 | |
| 5 | 16 | 6 | 10 | 13.48 | 13.08 | 16.92 | 67,555 | 68,271 | 66,755 | 67,364 | |
| 6 | 18 | 8 | 10 | 13.48 | 12.08 | 15.92 | 67,723 | 68,444 | 66,903 | 67,516 | |
| 7 | 20 | 8 | 12 | 13.08 | 12.08 | 15.92 | 68,042 | 68,769 | 67,182 | 67,799 | |
| 8 | 22 | 8 | 14 | 12.51 | 12.08 | 15.92 | 68,218 | 68,949 | 67,336 | 67,957 | |
| 9 | 24 | 10 | 14 | 12.51 | 11.08 | 14.92 | 68,260 | 68,994 | 67,376 | 67,998 | |
| Group | 10 | 8 | 2 | 6 | 13.75 | 13.08 | 18.92 | 65,604 | 66,292 | 65,068 | 65,657 |
| II | 11 | 10 | 2 | 8 | 14.08 | 13.08 | 18.92 | 66,264 | 66,961 | 65,637 | 66,232 |
| 12 | 12 | 2 | 10 | 13.88 | 13.08 | 18.92 | 66,753 | 67,457 | 66,060 | 66,660 | |
| 13 | 14 | 4 | 10 | 13.48 | 14.08 | 17.92 | 67,236 | 67,946 | 66,477 | 67,082 | |
| 14 | 16 | 4 | 12 | 13.75 | 12.08 | 17.92 | 67,556 | 68,272 | 66,756 | 67,366 | |
| 15 | 18 | 6 | 12 | 13.75 | 11.08 | 16.92 | 67,725 | 68,445 | 66,904 | 67,517 | |
| 16 | 20 | 6 | 14 | 13.37 | 11.08 | 16.92 | 68,045 | 68,771 | 67,184 | 67,800 | |
| 17 | 22 | 6 | 16 | 12.83 | 11.08 | 16.92 | 68,217 | 68,948 | 67,336 | 67,956 | |
| 18 | 24 | 8 | 16 | 12.83 | 10.08 | 15.92 | 68,259 | 68,993 | 67,375 | 67,998 | |
Section Properties
Beam Type 3 -- 7" Web
| Section Area = | 420.9 | in2 |
| ||||||||||||||||
| Section = | 17.31 | in | |||||||||||||||||
| = | 66,991 | in4 | |||||||||||||||||
| Depth= | 39 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 13.31 | 14.31 | 17.69 | 70,792 | 71,464 | 70,251 | 70,826 |
| I | 2 | 10 | 4 | 6 | 13.98 | 14.31 | 17.69 | 71,477 | 72,156 | 70,841 | 71,420 |
| 3 | 12 | 4 | 8 | 13.81 | 14.31 | 17.69 | 71,985 | 72,670 | 71,279 | 71,864 | |
| 4 | 14 | 6 | 8 | 13.81 | 13.31 | 16.69 | 72,326 | 73,016 | 71,575 | 72,163 | |
| 5 | 16 | 6 | 10 | 13.71 | 13.31 | 16.69 | 72,823 | 73,520 | 72,006 | 72,599 | |
| 6 | 18 | 8 | 10 | 13.71 | 12.31 | 15.69 | 73,006 | 73,707 | 72,166 | 72,762 | |
| 7 | 20 | 8 | 12 | 13.31 | 12.31 | 15.69 | 73,342 | 74,049 | 72,459 | 73,060 | |
| 8 | 22 | 8 | 14 | 12.74 | 12.31 | 15.69 | 73,532 | 74,242 | 72,626 | 73,229 | |
| 9 | 24 | 10 | 14 | 12.74 | 11.31 | 14.69 | 73,584 | 74,298 | 72,675 | 73,280 | |
| Group | 10 | 8 | 2 | 6 | 13.98 | 13.31 | 18.69 | 70,793 | 71,465 | 70,252 | 70,826 |
| II | 11 | 10 | 2 | 8 | 14.31 | 13.31 | 18.69 | 71,476 | 72,155 | 70,840 | 71,420 |
| 12 | 12 | 2 | 10 | 14.11 | 13.31 | 18.69 | 71,985 | 72,670 | 71,279 | 71,864 | |
| 13 | 14 | 4 | 10 | 13.71 | 14.31 | 17.69 | 72,487 | 73,178 | 71,714 | 72,303 | |
| 14 | 16 | 4 | 12 | 13.98 | 12.31 | 17.69 | 72,825 | 73,522 | 72,007 | 72,600 | |
| 15 | 18 | 6 | 12 | 13.98 | 11.31 | 16.69 | 73,007 | 73,708 | 72,167 | 72,764 | |
| 16 | 20 | 6 | 14 | 13.60 | 11.31 | 16.69 | 73,344 | 74,051 | 72,461 | 73,061 | |
| 17 | 22 | 6 | 16 | 13.06 | 11.31 | 16.69 | 73,531 | 74,242 | 72,625 | 73,229 | |
| 18 | 24 | 8 | 16 | 13.06 | 10.31 | 15.69 | 73,584 | 74,298 | 72,674 | 73,280 | |
Section Properties
Beam Type 3 -- 8" Web
| Section Area = | 459.9 | in2 |
| ||||||||||||||||
| Section = | 17.49 | in | |||||||||||||||||
| = | 72,106 | in4 | |||||||||||||||||
| Depth= | 39 | in | |||||||||||||||||
| Strand Size= | 0.60 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 13.49 | 14.49 | 17.51 | 75,940 | 76,598 | 75,394 | 75,957 |
| I | 2 | 10 | 4 | 6 | 14.16 | 14.49 | 17.51 | 76,642 | 77,307 | 75,999 | 76,567 |
| 3 | 12 | 4 | 8 | 13.99 | 14.49 | 17.51 | 77,166 | 77,837 | 76,451 | 77,023 | |
| 4 | 14 | 6 | 8 | 13.99 | 13.49 | 16.51 | 77,520 | 78,196 | 76,758 | 77,334 | |
| 5 | 16 | 6 | 10 | 13.89 | 13.49 | 16.51 | 78,034 | 78,716 | 77,203 | 77,783 | |
| 6 | 18 | 8 | 10 | 13.89 | 12.49 | 15.51 | 78,229 | 78,914 | 77,373 | 77,956 | |
| 7 | 20 | 8 | 12 | 13.49 | 12.49 | 15.51 | 78,580 | 79,270 | 77,678 | 78,265 | |
| 8 | 22 | 8 | 14 | 12.92 | 12.49 | 15.51 | 78,781 | 79,475 | 77,855 | 78,445 | |
| 9 | 24 | 10 | 14 | 12.92 | 11.49 | 14.51 | 78,843 | 79,540 | 77,911 | 78,504 | |
| Group | 10 | 8 | 2 | 6 | 14.16 | 13.49 | 18.51 | 75,941 | 76,599 | 75,395 | 75,958 |
| II | 11 | 10 | 2 | 8 | 14.49 | 13.49 | 18.51 | 76,641 | 77,306 | 75,998 | 76,566 |
| 12 | 12 | 2 | 10 | 14.29 | 13.49 | 18.51 | 77,166 | 77,837 | 76,451 | 77,023 | |
| 13 | 14 | 4 | 10 | 13.89 | 14.49 | 17.51 | 77,684 | 78,361 | 76,899 | 77,476 | |
| 14 | 16 | 4 | 12 | 14.16 | 12.49 | 17.51 | 78,036 | 78,718 | 77,204 | 77,785 | |
| 15 | 18 | 6 | 12 | 14.16 | 11.49 | 16.51 | 78,230 | 78,916 | 77,374 | 77,957 | |
| 16 | 20 | 6 | 14 | 13.78 | 11.49 | 16.51 | 78,582 | 79,273 | 77,680 | 78,267 | |
| 17 | 22 | 6 | 16 | 13.24 | 11.49 | 16.51 | 78,780 | 79,475 | 77,854 | 78,444 | |
| 18 | 24 | 8 | 16 | 13.24 | 10.49 | 15.51 | 78,842 | 79,540 | 77,911 | 78,503 | |
Section Properties
Beam Type 4 -- 6" Web
| Section Area = | 428.9 | in2 |
| ||||||||||||||||
| Section = | 19.54 | in | |||||||||||||||||
| = | 92,450 | in4 | |||||||||||||||||
| Depth= | 45 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 15.54 | 16.54 | 21.46 | 97,723 | 98,691 | 96,972 | 97,800 |
| I | 2 | 10 | 4 | 6 | 16.21 | 16.54 | 21.46 | 98,623 | 99,602 | 97,748 | 98,583 |
| 3 | 12 | 4 | 8 | 16.04 | 16.54 | 21.46 | 99,318 | 100,305 | 98,347 | 99,189 | |
| 4 | 14 | 6 | 8 | 16.04 | 15.54 | 20.46 | 99,818 | 100,812 | 98,780 | 99,627 | |
| 5 | 16 | 6 | 10 | 15.94 | 15.54 | 20.46 | 100,497 | 101,501 | 99,369 | 100,223 | |
| 6 | 18 | 8 | 10 | 15.94 | 14.54 | 19.46 | 100,808 | 101,818 | 99,640 | 100,499 | |
| 7 | 20 | 8 | 12 | 15.54 | 14.54 | 19.46 | 101,297 | 102,314 | 100,066 | 100,930 | |
| 8 | 22 | 8 | 14 | 14.97 | 14.54 | 19.46 | 101,611 | 102,634 | 100,341 | 101,210 | |
| 9 | 24 | 8 | 16 | 15.29 | 12.54 | 19.46 | 101,761 | 102,789 | 100,475 | 101,347 | |
| 10 | 26 | 10 | 16 | 15.29 | 11.54 | 18.46 | 101,762 | 102,794 | 100,480 | 101,356 | |
| 11 | 28 | 10 | 18 | 15.32 | 9.54 | 18.46 | 101,633 | 102,667 | 100,372 | 101,250 | |
| Group | 12 | 8 | 2 | 6 | 16.21 | 15.54 | 22.46 | 97,724 | 98,692 | 96,973 | 97,801 |
| II | 13 | 10 | 2 | 8 | 16.54 | 15.54 | 22.46 | 98,622 | 99,601 | 97,747 | 98,582 |
| 14 | 12 | 4 | 8 | 16.04 | 16.54 | 21.46 | 99,318 | 100,305 | 98,347 | 99,189 | |
| 15 | 14 | 4 | 10 | 15.94 | 16.54 | 21.46 | 100,005 | 101,001 | 98,941 | 99,790 | |
| 16 | 16 | 4 | 12 | 16.21 | 14.54 | 21.46 | 100,499 | 101,503 | 99,370 | 100,224 | |
| 17 | 16 | 6 | 10 | 15.94 | 15.54 | 20.46 | 100,497 | 101,501 | 99,369 | 100,223 | |
| 18 | 18 | 6 | 12 | 16.21 | 13.54 | 20.46 | 100,810 | 101,819 | 99,641 | 100,500 | |
| 19 | 20 | 6 | 14 | 15.83 | 13.54 | 20.46 | 101,300 | 102,317 | 100,068 | 100,932 | |
| 20 | 22 | 6 | 16 | 15.29 | 13.54 | 20.46 | 101,610 | 102,633 | 100,340 | 101,209 | |
| 21 | 24 | 6 | 18 | 15.32 | 11.54 | 20.46 | 101,762 | 102,790 | 100,476 | 101,349 | |
| 22 | 26 | 6 | 20 | 15.14 | 9.54 | 20.46 | 101,762 | 102,794 | 100,480 | 101,356 | |
| 23 | 26 | 8 | 18 | 15.32 | 10.54 | 19.46 | 101,764 | 102,796 | 100,482 | 101,357 | |
| 24 | 28 | 6 | 22 | 14.81 | 7.54 | 20.46 | 101,629 | 102,663 | 100,369 | 101,246 | |
| 25 | 28 | 8 | 20 | 15.14 | 8.54 | 19.46 | 101,631 | 102,666 | 100,371 | 101,248 | |
| 26 | 30 | 8 | 22 | 14.81 | 6.54 | 19.46 | 101,381 | 102,417 | 100,158 | 101,037 | |
| 27 | 32 | 8 | 24 | 14.37 | 4.54 | 19.46 | 101,033 | 102,069 | 99,860 | 100,739 | |
Section Properties
Beam Type 4 -- 7" Web
| Section Area = | 473.9 | in2 |
| ||||||||||||||||
| Section = | 19.82 | in | |||||||||||||||||
| = | 100,400 | in4 | |||||||||||||||||
| Depth= | 45 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 15.82 | 16.82 | 21.18 | 105,729 | 106,673 | 104,971 | 105,778 |
| I | 2 | 10 | 4 | 6 | 16.49 | 16.82 | 21.18 | 106,661 | 107,614 | 105,773 | 106,587 |
| 3 | 12 | 4 | 8 | 16.32 | 16.82 | 21.18 | 107,384 | 108,345 | 106,396 | 107,216 | |
| 4 | 14 | 6 | 8 | 16.32 | 15.82 | 20.18 | 107,908 | 108,876 | 106,850 | 107,675 | |
| 5 | 16 | 6 | 10 | 16.22 | 15.82 | 20.18 | 108,617 | 109,593 | 107,464 | 108,295 | |
| 6 | 18 | 8 | 10 | 16.22 | 14.82 | 19.18 | 108,950 | 109,931 | 107,753 | 108,589 | |
| 7 | 20 | 8 | 12 | 15.82 | 14.82 | 19.18 | 109,464 | 110,453 | 108,201 | 109,041 | |
| 8 | 22 | 8 | 14 | 15.25 | 14.82 | 19.18 | 109,801 | 110,795 | 108,495 | 109,340 | |
| 9 | 24 | 8 | 16 | 15.57 | 12.82 | 19.18 | 109,968 | 110,967 | 108,644 | 109,492 | |
| 10 | 26 | 10 | 16 | 15.57 | 11.82 | 18.18 | 109,984 | 110,986 | 108,661 | 109,512 | |
| 11 | 28 | 10 | 18 | 15.60 | 9.82 | 18.18 | 109,864 | 110,869 | 108,562 | 109,415 | |
| Group | 12 | 8 | 2 | 6 | 16.49 | 15.82 | 22.18 | 105,730 | 106,674 | 104,971 | 105,779 |
| II | 13 | 10 | 2 | 8 | 16.82 | 15.82 | 22.18 | 106,660 | 107,613 | 105,772 | 106,586 |
| 14 | 12 | 4 | 8 | 16.32 | 16.82 | 21.18 | 107,384 | 108,345 | 106,396 | 107,216 | |
| 15 | 14 | 4 | 10 | 16.22 | 16.82 | 21.18 | 108,100 | 109,069 | 107,015 | 107,841 | |
| 16 | 16 | 4 | 12 | 16.49 | 14.82 | 21.18 | 108,619 | 109,595 | 107,465 | 108,296 | |
| 17 | 16 | 6 | 10 | 16.22 | 15.82 | 20.18 | 108,617 | 109,593 | 107,464 | 108,295 | |
| 18 | 18 | 6 | 12 | 16.49 | 13.82 | 20.18 | 108,951 | 109,933 | 107,755 | 108,590 | |
| 19 | 20 | 6 | 14 | 16.11 | 13.82 | 20.18 | 109,467 | 110,456 | 108,203 | 109,044 | |
| 20 | 22 | 6 | 16 | 15.57 | 13.82 | 20.18 | 109,800 | 110,794 | 108,484 | 109,339 | |
| 21 | 24 | 6 | 18 | 15.60 | 11.82 | 20.18 | 109,970 | 110,969 | 108,645 | 109,494 | |
| 22 | 26 | 6 | 20 | 15.42 | 9.82 | 20.18 | 109,984 | 110,986 | 108,661 | 109,512 | |
| 23 | 26 | 8 | 18 | 15.60 | 10.82 | 19.18 | 109,985 | 110,988 | 108,663 | 109,514 | |
| 24 | 28 | 6 | 22 | 15.09 | 7.82 | 20.18 | 109,860 | 110,865 | 108,559 | 109,411 | |
| 25 | 28 | 8 | 20 | 15.42 | 8.82 | 19.18 | 109,862 | 110,867 | 108,561 | 109,413 | |
| 26 | 30 | 8 | 22 | 15.09 | 6.82 | 19.18 | 109,618 | 110,624 | 108,353 | 109,207 | |
| 27 | 32 | 8 | 24 | 14.65 | 4.82 | 19.18 | 109,271 | 110,278 | 108,056 | 108,910 | |
Section Properties
Beam Type 4 -- 8" Web
| Section Area = | 518.9 | in2 |
| ||||||||||||||||
| Section = | 20.06 | in | |||||||||||||||||
| = | 108,288 | in4 | |||||||||||||||||
| Depth= | 45 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Cont. | Iinitial | Ifinal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#5 |
A1 Bars 2-#6 |
A1 Bars 2-#5 |
A1 Bars 2-#6 |
| Group | 1 | 8 | 4 | 4 | 16.06 | 17.06 | 20.94 | 113,668 | 114,591 | 112,902 | 113,692 |
| I | 2 | 10 | 4 | 6 | 16.73 | 17.06 | 20.94 | 114,627 | 115,559 | 113,727 | 114,523 |
| 3 | 12 | 4 | 8 | 16.56 | 17.06 | 20.94 | 115,375 | 116,314 | 114,372 | 115,174 | |
| 4 | 14 | 6 | 8 | 16.56 | 16.06 | 19.94 | 115,921 | 116,866 | 114,844 | 115,651 | |
| 5 | 16 | 6 | 10 | 16.46 | 16.06 | 19.94 | 116,655 | 117,608 | 115,480 | 116,291 | |
| 6 | 18 | 8 | 10 | 16.46 | 15.06 | 18.94 | 117,007 | 117,965 | 115,786 | 116,601 | |
| 7 | 20 | 8 | 12 | 16.06 | 15.06 | 18.94 | 117,544 | 118,509 | 116,252 | 117,073 | |
| 8 | 22 | 8 | 14 | 15.49 | 15.06 | 18.94 | 117,900 | 118,870 | 116,563 | 117,387 | |
| 9 | 24 | 8 | 16 | 15.81 | 13.06 | 18.94 | 118,084 | 119,058 | 119,725 | 117,553 | |
| 10 | 26 | 10 | 16 | 15.81 | 12.06 | 17.94 | 118,112 | 119,089 | 116,754 | 117,584 | |
| 11 | 28 | 10 | 18 | 15.84 | 10.06 | 17.94 | 118,001 | 118,981 | 116,662 | 117,494 | |
| Group | 12 | 8 | 2 | 6 | 16.73 | 16.06 | 21.94 | 113,669 | 114,592 | 112,903 | 113,693 |
| II | 13 | 10 | 2 | 8 | 17.06 | 16.06 | 21.94 | 114,626 | 115,558 | 113,726 | 114,522 |
| 14 | 12 | 4 | 8 | 16.56 | 17.06 | 20.94 | 115,375 | 116,314 | 114,372 | 115,174 | |
| 15 | 14 | 4 | 10 | 16.46 | 17.06 | 20.94 | 116,116 | 117,062 | 115,012 | 115,819 | |
| 16 | 16 | 4 | 12 | 16.73 | 15.06 | 20.94 | 116,657 | 117,610 | 115,481 | 116,293 | |
| 17 | 16 | 6 | 10 | 16.46 | 16.06 | 19.94 | 116,655 | 117,608 | 115,480 | 116,291 | |
| 18 | 18 | 6 | 12 | 16.73 | 14.06 | 19.94 | 117,009 | 117,967 | 115,787 | 116,603 | |
| 19 | 20 | 6 | 14 | 16.35 | 14.06 | 19.94 | 117,547 | 118,512 | 116,255 | 117,075 | |
| 20 | 22 | 6 | 16 | 15.81 | 14.06 | 19.94 | 117,899 | 118,869 | 116,562 | 117,387 | |
| 21 | 24 | 6 | 18 | 15.84 | 12.06 | 19.94 | 118,085 | 119,059 | 116,727 | 117,554 | |
| 22 | 26 | 6 | 20 | 15.66 | 10.06 | 19.94 | 118,112 | 119,089 | 116,754 | 117,584 | |
| 23 | 26 | 8 | 18 | 15.84 | 11.06 | 18.94 | 118,113 | 119,091 | 116,755 | 117,585 | |
| 24 | 28 | 6 | 22 | 15.33 | 8.06 | 19.94 | 117,997 | 118,977 | 116,659 | 117,490 | |
| 25 | 28 | 8 | 20 | 15.66 | 9.06 | 18.94 | 117,999 | 118,979 | 116,661 | 117,493 | |
| 26 | 30 | 8 | 22 | 15.33 | 7.06 | 18.94 | 117,760 | 118,742 | 116,458 | 117,291 | |
| 27 | 32 | 8 | 24 | 14.89 | 5.06 | 18.94 | 117,415 | 118,397 | 116,163 | 116,996 | |
Section Properties
Beam Type 6 -- 6.5" Web
| Section Area = | 643.6 | in2 |
| ||||||||||||||||
| Section = | 25.92 | in | |||||||||||||||||
| = | 235,735 | in4 | |||||||||||||||||
| Depth= | 54 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Iinitial | Ifinal | ||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#6 |
A1 Bars 2-#6 | |
| Group | 1 | 14 | 4 | 10 | 23.52 | 22.92 | 23.08 | 251,047 | 248,880 |
|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 16 | 4 | 12 | 23.25 | 22.92 | 23.08 | 252,425 | 250,070 |
| 3 | 18 | 6 | 12 | 23.25 | 21.92 | 22.08 | 253,525 | 251,022 | |
| 4 | 20 | 6 | 14 | 23.06 | 21.92 | 22.08 | 254,886 | 252,199 | |
| 5 | 22 | 6 | 16 | 22.92 | 21.92 | 22.08 | 256,238 | 253,370 | |
| 6 | 24 | 8 | 16 | 22.92 | 20.92 | 21.08 | 257,053 | 254,081 | |
| 7 | 26 | 8 | 18 | 22.59 | 20.92 | 21.08 | 258,130 | 255,017 | |
| 8 | 28 | 8 | 20 | 22.32 | 20.92 | 21.08 | 259,191 | 255,940 | |
| 9 | 30 | 10 | 20 | 22.32 | 19.92 | 20.08 | 259,751 | 256,433 | |
| 10 | 32 | 10 | 22 | 22.10 | 19.92 | 20.08 | 260,803 | 257,350 | |
| 11 | 34 | 10 | 24 | 21.75 | 19.92 | 20.08 | 261,604 | 258,052 | |
| 12 | 36 | 10 | 26 | 21.46 | 19.92 | 20.08 | 262,412 | 258,760 | |
| 13 | 38 | 12 | 26 | 21.46 | 18.92 | 19.08 | 262,739 | 259,053 |
Section Properties
Beam Type 6 -- 7.5" Web
| Section Area = | 697.6 | in2 |
| ||||||||||||||||
| Section = | 26.00 | in | |||||||||||||||||
| = | 248,915 | in4 | |||||||||||||||||
| Depth= | 54 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Iinitial | Ifinal | ||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#6 |
A1 Bars 2-#6 | |
| Group | 1 | 14 | 4 | 10 | 23.60 | 23.00 | 23.00 | 264,293 | 262,115 |
|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 16 | 4 | 12 | 23.33 | 23.00 | 23.00 | 265,686 | 263,318 |
| 3 | 18 | 6 | 12 | 23.33 | 22.00 | 22.00 | 266,801 | 264,281 | |
| 4 | 20 | 6 | 14 | 23.14 | 22.00 | 22.00 | 268,178 | 265,473 | |
| 5 | 22 | 6 | 16 | 23.00 | 22.00 | 22.00 | 269,548 | 266,658 | |
| 6 | 24 | 8 | 16 | 23.00 | 21.00 | 21.00 | 270,378 | 267,381 | |
| 7 | 26 | 8 | 18 | 22.67 | 21.00 | 21.00 | 271,472 | 268,330 | |
| 8 | 28 | 8 | 20 | 22.40 | 21.00 | 21.00 | 272,551 | 269,269 | |
| 9 | 30 | 10 | 20 | 22.40 | 20.00 | 20.00 | 273,125 | 269,772 | |
| 10 | 32 | 10 | 22 | 22.18 | 20.00 | 20.00 | 274,195 | 270,705 | |
| 11 | 34 | 10 | 24 | 21.83 | 20.00 | 20.00 | 275,014 | 271,420 | |
| 12 | 36 | 10 | 26 | 21.54 | 20.00 | 20.00 | 275,839 | 272,143 | |
| 13 | 38 | 12 | 26 | 21.54 | 19.00 | 19.00 | 276,180 | 272,447 |
Section Properties
Beam Type 6 -- 8.5" Web
| Section Area = | 751.6 | in2 |
| ||||||||||||||||
| Section = | 26.07 | in | |||||||||||||||||
| = | 262,087 | in4 | |||||||||||||||||
| Depth= | 54 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Iinitial | Ifinal | ||||||||
| # | T | H | S | e1 | e2 | e3 | A1 Bars 2-#6 |
A1 Bars 2-#6 | |
| Group | 1 | 14 | 4 | 10 | 23.67 | 23.07 | 22.93 | 277,522 | 275,336 |
|---|---|---|---|---|---|---|---|---|---|
| I | 2 | 16 | 4 | 12 | 23.40 | 23.07 | 22.93 | 278,930 | 276,549 |
| 3 | 18 | 6 | 12 | 23.40 | 22.07 | 21.93 | 280,057 | 277,523 | |
| 4 | 20 | 6 | 14 | 23.21 | 22.07 | 21.93 | 281,449 | 278,727 | |
| 5 | 22 | 6 | 16 | 23.07 | 22.07 | 21.93 | 282,834 | 279,925 | |
| 6 | 24 | 8 | 16 | 23.07 | 21.07 | 20.93 | 283,678 | 280,658 | |
| 7 | 26 | 8 | 18 | 22.74 | 21.07 | 20.93 | 284,786 | 281,620 | |
| 8 | 28 | 8 | 20 | 22.47 | 21.07 | 20.93 | 285,881 | 282,571 | |
| 9 | 30 | 10 | 20 | 22.47 | 20.07 | 19.93 | 286,468 | 283,085 | |
| 10 | 32 | 10 | 22 | 22.25 | 20.07 | 19.93 | 287,554 | 284,030 | |
| 11 | 34 | 10 | 24 | 21.90 | 20.07 | 19.93 | 288,388 | 284,758 | |
| 12 | 36 | 10 | 26 | 21.61 | 20.07 | 19.93 | 289,228 | 285,493 | |
| 13 | 38 | 12 | 26 | 21.61 | 19.07 | 18.93 | 289,581 | 285,807 |
Section Properties
Beam Type 7 -- 6" Web
Bulb Tee Girder
| Section Area = | 787.4 | in2 |
| ||||||||||||||||
| Section = | 37.58 | in | |||||||||||||||||
| = | 571,047 | in4 | |||||||||||||||||
| Depth= | 72.5 | in | |||||||||||||||||
| Strand Size= | 0.6 | in | |||||||||||||||||
| = | 5 | ksi | |||||||||||||||||
| = | 7 | ksi |
| Cont. | Iinitial | Ifinal | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Span | # | T | H | S | e1 | e2 | e3 | A1 Bars 4-#6 |
A1 Bars 4-#6 |
| Group | 1 | 14 | 4 | 10 | 35.58 | 34.58 | 29.92 | 609,994 | 604,448 |
| I | 2 | 16 | 4 | 12 | 35.25 | 34.58 | 29.92 | 613,316 | 607,307 |
| 3 | 18 | 6 | 12 | 35.25 | 33.58 | 28.92 | 616,196 | 609,790 | |
| 4 | 20 | 6 | 14 | 35.01 | 33.58 | 28.92 | 619,469 | 612,612 | |
| 5 | 22 | 6 | 16 | 34.83 | 33.58 | 28.92 | 622,719 | 615,417 | |
| 6 | 24 | 8 | 16 | 34.83 | 32.58 | 27.92 | 625,140 | 617,512 | |
| 7 | 26 | 8 | 18 | 34.69 | 32.58 | 27.92 | 628,347 | 620,286 | |
| 8 | 28 | 8 | 20 | 34.58 | 32.58 | 27.92 | 631,536 | 623,046 | |
| 9 | 30 | 10 | 20 | 34.58 | 31.58 | 26.92 | 633,518 | 624,769 | |
| 10 | 32 | 10 | 22 | 34.31 | 31.58 | 26.92 | 636,280 | 627,166 | |
| 11 | 34 | 10 | 24 | 34.08 | 31.58 | 26.92 | 639,012 | 629,539 | |
| 12 | 36 | 10 | 26 | 33.89 | 31.58 | 26.92 | 641,737 | 631,909 | |
| 13 | 38 | 10 | 28 | 33.58 | 31.58 | 26.92 | 644,052 | 633,926 | |
| 14 | 40 | 12 | 28 | 33.58 | 30.58 | 25.92 | 645,607 | 635,289 |
751.22.3.6 Girder Reinforcement
| TABLE OF DIMENSIONS | |||||||||||||
| BEAM TYPE 2 | BEAM TYPE 3 | BEAM TYPE 4 | BEAM TYPE 6 | BEAM TYPE 7 | |||||||||
| WEB | 6" | 7" | 8" | 6" | 7" | 8" | 6" | 7" | 8" | 6½" | 7½" | 8½" | 6" |
| "a" | 5½" | 5½" | 5½" | 5½" | 5½" | 5½" | 5½" | 5½" | 5½" | 8¾" | 8¾" | 8¾" | 10" |
| "b" | 4" | 4" | 4" | 4" | 4" | 4" | 4" | 4" | 4" | 4" | 4" | 4" | 4" |
| "c" | 6" | 6" | 6" | 6" | 6" | 6" | 6" | 6" | 6" | 7" | 7" | 7" | 4½" |
| "d" | 3¼" | 3¼" | 3¼" | 5⅛" | 5⅛" | 5⅛" | 6¼" | 6¼" | 6¼" | 4⅛" | 4⅛" | 4⅛" | 4⅛" |
| "e" | 13" | 14" | 15" | 13" | 14" | 15" | 13" | 14" | 15" | 18" | 19" | 20" | 20" |
| "f" | 2" | 2" | 2" | 2" | 2" | 2" | 2" | 2" | 2" | 3" | 3" | 3" | 7¾" |
| "g" | 11" | 12" | 13" | 11" | 12" | 13" | 11" | 12" | 13" | 22" | 23" | 24" | 2'-11½" |
| "h" | 2'-6" | 2'-6" | 2'-6" | 3'-1" | 3'-1" | 3'-1" | 3'-7" | 3'-7" | 3'-7" | 4'-4" | 4'-4" | 4'-4" | 5'-10½" |
| "i" | 3'-0½" | 3'-0½" | 3'-0½" | 3'-7½" | 3'-7½" | 3'-7½" | 4'-1½" | 4'-1½" | 4'-1½" | 4'-10½" | 4'-10½" | 4'-10½" | 6'-5" |
| TOTAL BAR LENGTH | |||||||||||||
| BEAM TYPE 2 | BEAM TYPE 3 | BEAM TYPE 4 | BEAM TYPE 6 | BEAM TYPE 7 | |||||||||
| WEB | 6" | 7" | 8" | 6" | 7" | 8" | 6" | 7" | 8" | 6½" | 7½" | 8½" | 6" |
| B1 | 4'-1" | 4'-1" | 4'-1" | 4'-8" | 4'-8" | 4'-8" | 5'-2" | 5'-2" | 5'-2" | 5'-11" | 5'-11" | 5'-11" | 7'-8" |
| B2 | 3'-6" | 3'-6" | 3'-6" | 4'-1" | 4'-1" | 4'-1" | 4'-7" | 4'-7" | 4'-7" | 5'-4" | 5'-4" | 5'-4" | 7'-0" |
| C1 | 13" | 14" | 15" | 13" | 14" | 15" | 13" | 14" | 15" | 2'-2" | 2'-3" | 2'-4" | 3'-6" |
| D1 | 2'-4" | 2'-5" | 2'-6" | 2'-5" | 2'-6" | 2'-7" | 2'-7" | 2'-8" | 2'-9" | 3'-0" | 3'-1" | 3'-2" | 3'-1" |
Note: For girders that have stepped flanges, create new B1 and C1 Bars and adjust Bar Lengths for step heights.

|

|

|
| C1 BAR
(Beam Types 2-6) |
C1 BAR
(Beam Type 7) | |
| B1 & B2 BAR | 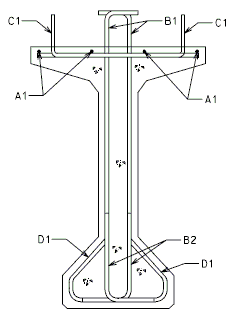
| |
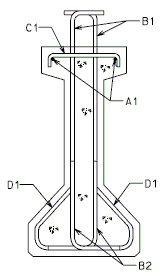
|

| |
| D1 BAR | ||
| SECTION THRU GIRDER
(Typ. for MoDOT Standard Girder Types 2-6) |
SECTION THRU GIRDER
(MoDOT Standard Girder Type 7) |
Welded Wire Reinforcing Steel Details for NU Standard Girders
(See Bridge Standard Drawings for details.)
Alternate Bar Reinforcing Steel Details for NU Standard Girders
Alternate bar reinforcing steel details shall be provided for all NU girders for all spans.
Details shall be similar to details provided for MoDOT Standard Girders:
- End section reinforcement shall be designed using #6 B2 Bars @ 3 ½” cts.
- C1 bars shall be straight bars without legs.
- All B1 bars shall be epoxy coated.
- B1 bars shall be #4 or #5 bar maximum. (#4 bars are preferred to allow permissible alternate bar shape.)
Section Reinforcement Details
(Typ. for MoDOT Standard Girder Types 2 thru 6 and NU Standard Girders.)

| |
| MILD STEEL REINFORCEMENT |
Guidance: For MoDOT Standard Girder Types 7 or 8, using #6 B1 bars does not provide 1” clearance when center strands are spaced 1” off centerline of girder between hold down devices because of bend radius of #6 bar. Use of #5 bar is preferred. For NU Standard Girders and alternate bar reinforcing steel details, use of #5 bar is preferred similarly. |
| Note: B1, B2 and D1 bars shall be placed in pairs. A note on the girder sheet gives the fabricator the option of furnishing the 2-D1 bars as one bar. | |

|
| B1 BAR PERMISSIBLE ALTERNATE SHAPE |
| Note: Place the above detail on Prestress I-Girder sheets only where #4-B1 reinforcing bars are used. |
Anchorage Zone Reinforcement
The following details meet the criteria for anchorage zone reinforcement for pretensioned girders in EPG 751.22.2.4 for all MoDOT and NU standard girder shapes.
MoDOT Standard Girder End Section Reinforcement
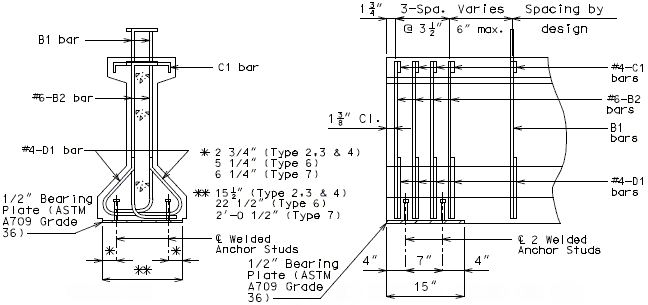
NU Standard Girder End Section Reinforcement
Typical end section reinforcement shall be all welded wire reinforcement (WWR) or all deformed bars. If additional reinforcement is required with WWR, the following options shall be considered.
Minimum spacing of reinforcing bars shall be in accordance with LRFD 5.10.3.1.2.
Consideration shall be given to spacing reinforcing bars 1” clear from welded studs on bearing plates (not shown).
Bearing Plate Anchor Studs
The standard ½" bearing plate will be anchored with four ½" x 4" studs for MoDOT shapes and eight ½” x 5” studs for NU shapes.
If required, increase the number of ½" studs and space between open B2 bars.
The minimum ¼" fillet weld between the ½" bearing plate and 1½" sole plate is adequate for all cases.
LFD Seismic Design
Studs shall be designed to meet the criteria of 2002 AASHTO 17th Edition Division I-A in Seismic Performance Category C or D.
Stud capacity is determined as follows for:
- Stud Cap. = (n)(As)(0.4Fy)(1.5)
- Where:
- N = number of studs
- As = area of stud
- Fy = yield strength of stud (50 ksi)
- 0.4Fy = Allowable Shear in Pins AASHTO Table 10.32.1A
- 1.5 = seismic overload factor
- Where:
If required, increase the number of 1/2” studs to six and space between open B2 bars or WWF. If this is still not adequate, 5/8” studs may be used. The following table may be used as a guide for upper limits of dead load reactions:
| No. of Studs | Stud Dia. | Max Allowable D.L Reaction (kips) | |
|---|---|---|---|
| A = 0.30 | A = 0.36 | ||
| 4 | 1/2” | 78 | 65 |
| 6 | 1/2” | 117 | 98 |
| 4 | 5/8” | 122 | 102 |
| 6 | 5/8” | 184 | 153 |
| 8 | 1/2” | 156 | 130 |
| 10 | 1/2” | 195 | 163 |
| 8 | 5/8” | 244 | 204 |
| 10 | 5/8” | 306 | 255 |
751.22.3.7 Bent-up Strands
Bent-up strands for positive moment connection
Tables below show the number of bent-up strands for closed and open diaphragms (with a continuous superstructure), respectively. Provide a minimum number of bent-up strands as shown in tables at the bottom of girder ends. These bent-up strands shall be adequate to resist a positive moment over the bents.
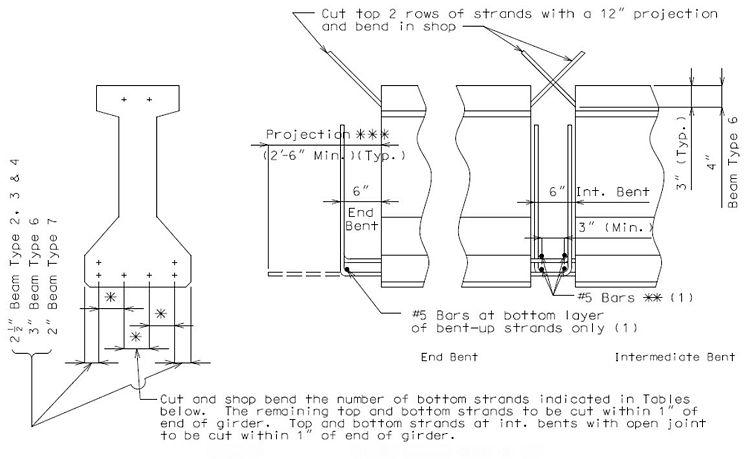
Varies
#5 bars typical at each layer of bent-up strands.
Use 3’-0” projection for NU Girders.
(1) #5-strand tie bars normal to girder.
| WEB THICKNESS (INCHES) |
NUMBER OF BOTTOM STRANDS FOR POSITIVE MOMENT CONNECTION (C) | ||||
| BEAM TYPE 2 | BEAM TYPE 3 | BEAM TYPE 4 | BEAM TYPE 6 | BEAM TYPE 7 (BULB TEE) | |
| 6 | 6 | 6 | 8 | --- | 12 |
| 6-1/2 | --- | --- | --- | 10 | --- |
| 7(A) | 6 | 8 | 8 | --- | --- |
| 7-1/2(B) | --- | --- | --- | 12 | --- |
| 8(A) | 6 | 8 | 10 | --- | --- |
| 8-1/2(B) | --- | --- | --- | 12 | --- |
- (A) Modified Beam Type 2, 3 or 4.
- (B) Modified Beam Type 6.
- (C) If available. Otherwise, bend all bottom strands.
| NUMBER OF BOTTOM STRANDS FOR POSITIVE MOMENT CONNECTION (C) | ||||
| NU 35 | 10 | |||
| NU 43 | 10 | |||
| NU 53 | 10 | |||
| NU 63 | 12 | |||
| NU 70 | 12 | |||
751.22.3.8 Haunching and Girder Steps
Haunching
Haunching for a P/S I-Girder bridge is the distance between the top of the girder and the bottom of the slab.
Haunching shall be computed at quarter (1/4) points for bridges with spans less than 75 feet, and at tenth (1/10) points for span 75 feet and longer. A typical theoretical slab haunching diagram as shown below shall be provided on all P/S I-Girder bridges.
For cast-in-place decks, a minimum haunch of 1" at the centerline of girder and 1/2" at the edge of the girder flange shall be provided to allow for construction tolerances and normal concrete variations. For NU and MoDOT Bulb Tee Standard Girders, the minimum haunch may need to be increased. See the Structural Project Manager or Structural Liaison Engineer for cast-in-place decks.
For precast prestressed panel decks, a minimum haunch of 1 1/8” shall be provided for MoDOT Standard Girders (Types 2, 3, 4, and 6) for the same reasons. Provide 1 ½” min. haunch for NU and MoDOT Bulb Tee Standard Girders. A minimum of 1" shall be made available below the precast prestressed panels to allow for adequate flow of concrete below the panel. This is accomplished by specifying and using 1” min. joint filler under the precast prestressed panels.
A maximum haunch at the centerline of the girder of 2.5" for MoDOT Type 2, 3, 4 and 6 girders or 4.5” for all NU and MoDOT Bulb Tee (Types 7 and 8) girders is allowed when prestressed panels are used, and 3.5" when only the cast-in-place option is used. (The maximum joint filler thickness to be used for supporting panels shall be 2" for MoDOT (Types 2, 3, 4 and 6) girders or 4” for all NU and MoDOT Bulb Tee (Types 7 and 8) girders; the remaining haunch thickness will be addressed by varying the slab thickness.)

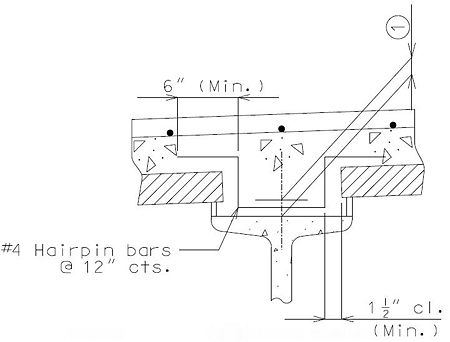
Girder Steps
Where haunches greater than 2.5" or 4.5", depending on girder type used, occur with prestressed panels, steps shall be provided on the girder as shown below, to keep the haunch less than 2" or 4" for MoDOT (Type 2, 3, 4 and 6) girders or all NU and Bulb Tee (Types 7 and 8) girders, respectively. The minimum step height shall be 1/2" with 1/2" increments with no limit of the number of steps. If the steps accumulate to 1" or more, adjust the height of the B1 bars or WWR in 1" increments. Length of WWR sections for NU girders should be based on shear and confinement requirements before adjusting height to avoid multiple short length sections.
| PART ELEVATION OF GIRDER | SECTION A-A |
Top of Girder
Tops of girders, for bridges with superelevations of more than 2%, shall be sloped across the top flange to match the superelevation as shown below. The minimum thickness of the top flange shall be the standard flange thickness and the overall height at the minimum point shall be the standard girder height.
NU and MoDOT Bulb Tee Standard Girder top flanges exceeding a 4% cross-slope may experience sweep after form removal because of the unsymmetrical section and a resulting imbalanced prestressed load. It is recommended that the flange thickness be increased to only half of that required (but less than or equal to 4% cross-slope) and the height difference mitigated using thicker joint filler on the high side. If thicker joint filler cannot be fully used to compensate for the height difference, the extra load of a thicker slab must be accounted for in the design of the girders.
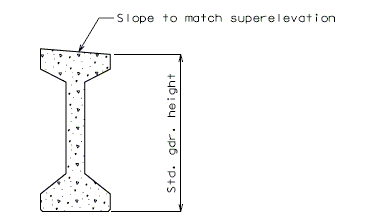
751.22.3.9 Open Intermediate Bent Diaphragms
(Expansion Intermediate Bent with Continuous Slab)
Dimensions:
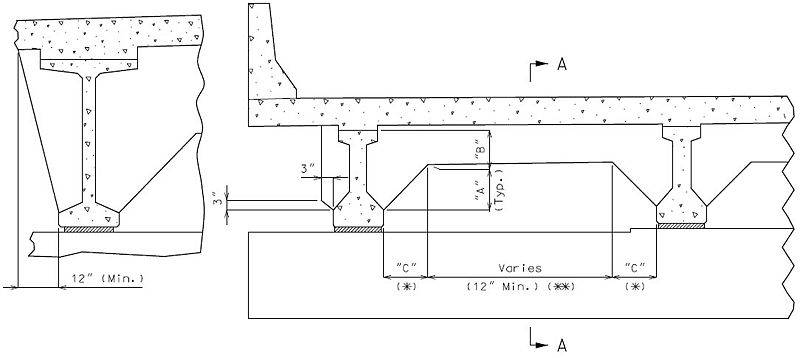
| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION |
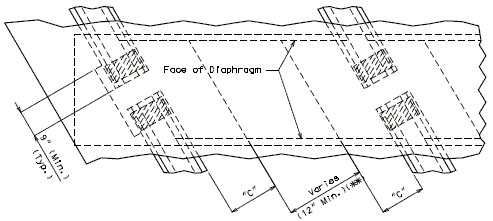
 PART SECTION A-A |
(*) A sloped diaphragm allows clearance for the future placement of jacks needed to replace bearings.
(**) For Bulb Tee Girder, spacings less than 8'-8" dimensions "A", "B" & "C" may have to be modified. (***) Make sure the diaphragm is wide enough to provide enough cover for the Coil Tie Rods. |
| |||||||||||||||||||||||||||
(Expansion Intermediate Bent with Continuous Slab)
Coil Tie Rod:


| PART SECTION A-A | DETAILS OF COIL TIE RODS IN BULB TEE GIRDERS |
(Expansion Intermediate Bent with Continuous Slab)
Reinforcement:

| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION |

| (1) For Bulb Tee Girders, the first #6 Bar shall be placed 10" from the centerline of Web (Top Flange will prevent some Bars from extending into the Slab). | 
|
| (*) See Section "A" for the placement of reinforcement. (**) Use the same clearance as longitudinal slab steel. |
PART SECTION A-A |
751.22.3.10 Closed Intermediate Bent Diaphragms
(Fixed Intermediate Bents with Continuous Slab)
Dimensions:

| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION |


(Showing Joint Filler)

|
(*) Make flush with Bent Caps less than 3'-0" wide. For Bent Caps 3'-0" and over, make Diaphragms 2'-6" wide unless skew requires wider Diaphragm to accommodate Coil Ties. (**) For tapered bearings or for bearings with different thickness use the following note: "Fill area under girders with Joint Filler." |
(Expansion Intermediate Bents with Continuous Slab)
Dimensions:

| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION |
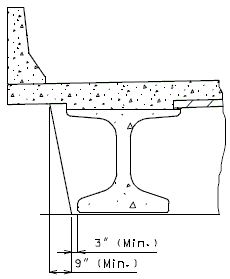


|
(*) Make flush with Bent Caps less than 3'-0" wide. For Bent Caps 3'-0" and over, make Diaphragm 2'-6" wide unless skew requires wider Diaphragm to accommodate Coil Ties.
(**) Use Shear Blocks when Bent Cap steps down in one direction or when there are less than two steps in each direction with maximum step height less than 1 1/2" each. Shear Blocks shall be detailed parallel to the centerline of roadway and shall be designed to resist 0.20 times the tributary weight where tributary weight is defined as the total bent dead load reaction. See this section for shear block design method. |
| PART LONGITUDINAL ELEVATION |
(Fixed and Expansion Intermediate Bents with Continuous Slab)
Reinforcement (Square Structure):

| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION |
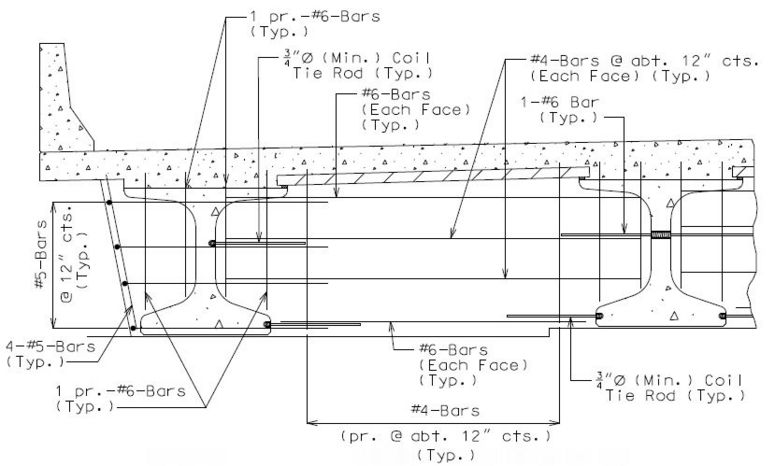
| (1) For Bulb Tee Girders, the #6 Bar shall be a min. of 15" from centerline of Girder and will not extend past the bottom of the top flange.
(2)For Bulb Tee Girders, use 3-#4 Bars in each Diaphragm face.
(*) #5 Bars for each layer of bent up strands. (**) Use the same clearance as the longitudinal slab steel. (***) By design, Min. #6 Dowel bars @ 12" cts. (Typ.) (Fixed bent only). |

|

|

|
| PART ELEVATION A-A | SECTION THRU DIAPHRAGM |
(Fixed and Expansion Intermediate Bents with Continuous Slab)
Reinforcement (Skewed Structure):

| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION |
| (1) For Bulb Tee Girders, the #6 Bar shall be a min. of 15" from centerline of Girder and will not extend past the bottom of the top flange.
(2)For Bulb Tee Girders, use 3-#4 Bars in each Diaphragm face.
(*) #5 Bars for each layer of bent up strands. (**) Omit leg on outside of exterior girder. (***) By design, Min. #6 Dowel bars @ 12" cts. (Typ.) (Fixed bent only). |

|

|

|
| SKEWS THRU 25 DEG. | SKEWS OVER 25 DEG. |
(Change in Girder Height at Fixed Bents)
Reinforcement:
Change girder heights within a continuous girder series only when specified on Design Layout or by Structural Project Manager.
Girder heights can only be changed at fixed bents for continuous series.
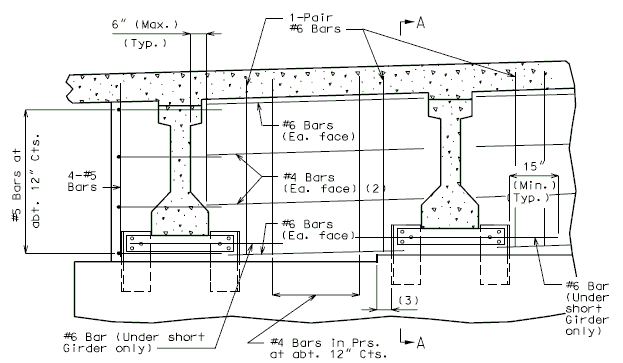
(*) By design, Min. #6 Dowel bars @ 12" Cts. (Typ.)
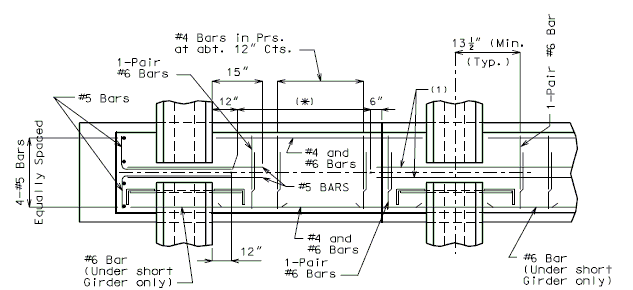
| (1) At each layer of bent strands.
(2) For Bulb Tee Girders, use 3-#4 Bars in each Diaphragm face. (3) 3" Min. when using beam step. (4) By design, Min. #6 @ 12" Cts. dowel bars (Typ.) |
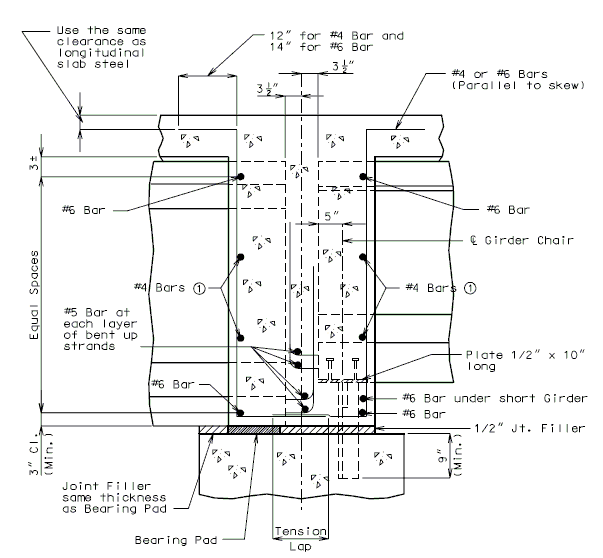
| Note: Girder heights can change a maximum of one Girder type.
(1) For Bulb Tee Girders, use 3-#4 Bars in each Diaphragm face. |
(Change in Girder Height at Fixed Bents)
Edge Distance Details:

| NOTE: | Field bending may be required for #4 and #6 H Bars in Skewed Structures near short Exterior Girder. |
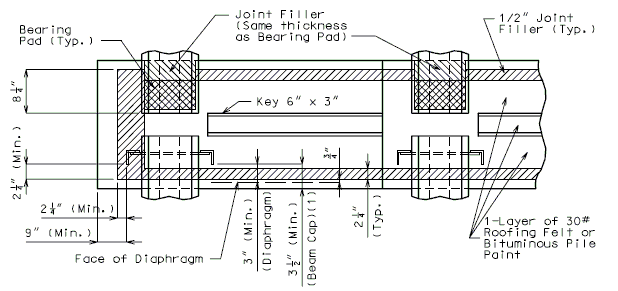
(1) When Beam width is controlled by Girder chair clearance, make Diaphragm Flush with Beam Cap.
(Change in Girder Height at Fixed Bents)
Girder Chair Details:

|

|
| PART END ELEVATION | |
| PART FRONT ELEVATION |
| SERVICE LOAD REACTIONS | VERTICAL ANGLE | HORIZONTAL BAR |
| 90 Kips | 8 x 6 x 1/2 | 7" x 7/8" |
- Use DC (non-composite loads) and 50#/Sq.Ft.
- Construction Load for Reactions.
- (*) 3" Min. when using beam step.
3/4" Chamfer and 1/2" Joint Filler

INTERMEDIATE DIAPHRAGMS

751.22.3.11 Non-integral End Bent Diaphragms
(End Diaphragm with no Expansion Devices)
Dimensions:
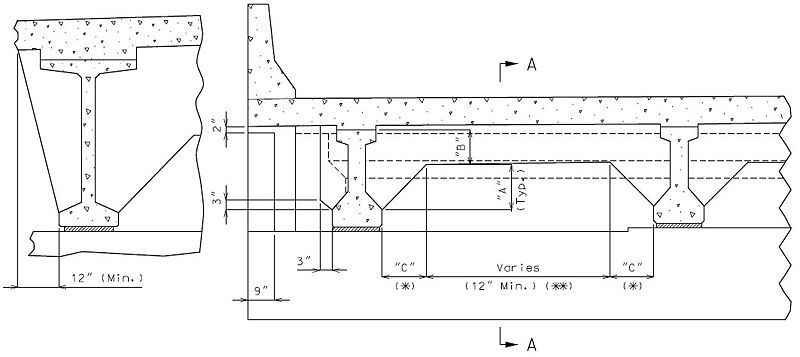
| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION NEAR END BENT |
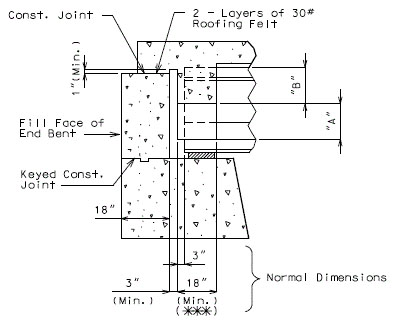 PART SECTION A-A |
(*) A sloped diaphragm allows clearance for the future placement of jacks needed to replace bearings. (**) For Bulb Tee Girder, spacings less than 8'-8" dimensions "A", "B" & "C" may have to be modified. |
| |||||||||||||||||||||||||||
(End Diaphragm with no Expansion Devices)
Coil Tie Rods:

| NOTE: | For location of the Coil Tie Rods in a plan view, see Coil Ties. |
| (*) 6" (Min.) shall be used for all I-Girders and Bulb Tee Girders. |
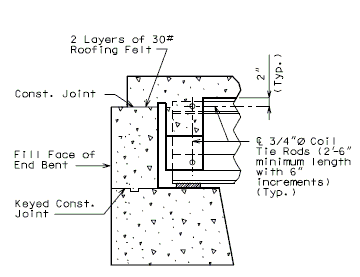
|
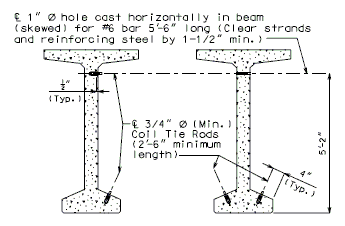
| |
| EXTERIOR GIRDERS | INTERIOR GIRDERS | |
| PART SECTION A-A | DETAILS OF COIL TIE RODS IN BULB TEE GIRDERS | |
(End Diaphragm with no Expansion Devices)
Reinforcement:
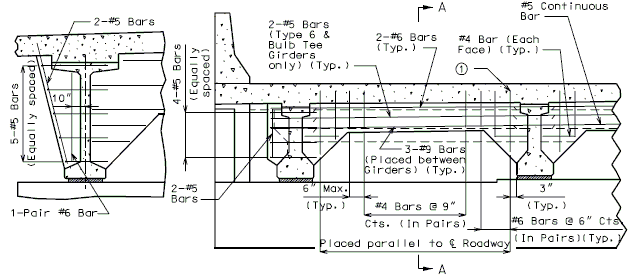
| PART ELEVATION NEAR END BENT FOR BULB TEE GIRDERS |
PART ELEVATION NEAR END BENT |
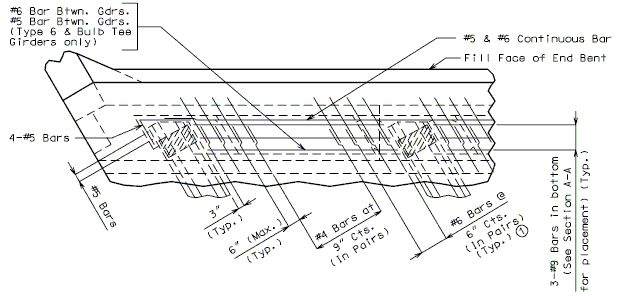
| (1) For Bulb Tee Girders, the first #6 Bar shall be placed 10" from the centerline of Web (Top Flange will prevent some Bars from extending into the Slab). | |
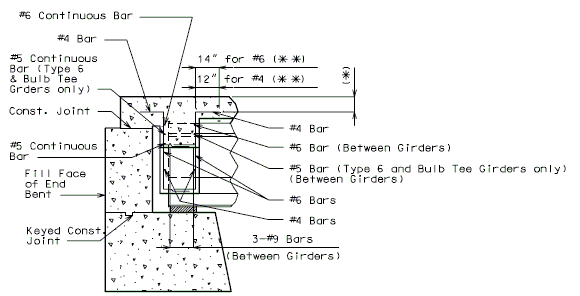
|
|
| NOTE: Bars across end of girders to be continuous. | |
| (*) Use the same clearance as longitudinal slab steel. (**) Show this dimension Bridge Plan Sheets. |
- PART SECTION A-A
(End Diaphragm with Expansion Devices)
Dimensions:
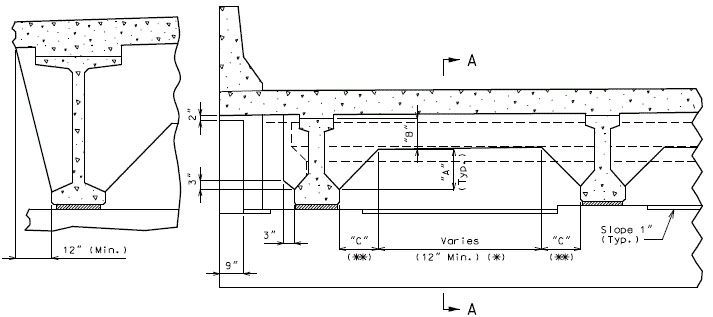
| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION NEAR END BENT |

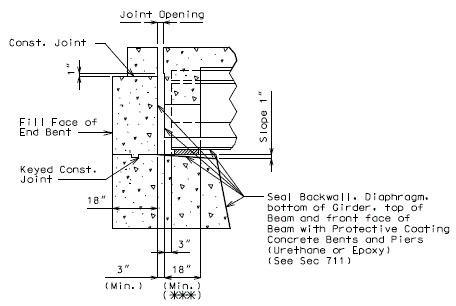 PART SECTION A-A |
(*) For Bulb Tee Girder, spacings less than 8'-8" dimensions "A", "B" & "C" may have to be modified. |
| |||||||||||||||||||||||||||
| (**) A sloped diaphragm allows clearance for the future placement of jacks needed to replace bearings. | |||||||||||||||||||||||||||||
| (***) Make sure the diaphragm is wide enough to provide cover for the coil tie rods. | |||||||||||||||||||||||||||||
(End Diaphragm with Expansion Devices)
Coil Tie Rods:

| NOTE: | For location of the Coil Tie Rods in a plan view, see Coil Ties. |
| (*) 6" (Min.) shall be used for all I-Girders and Bulb Tee Girders. |
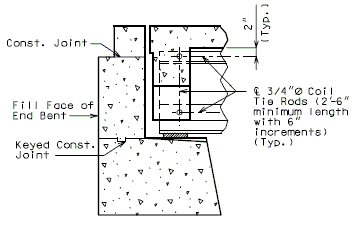
|
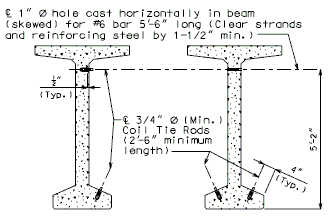
| |
| EXTERIOR GIRDERS | INTERIOR GIRDERS | |
| PART SECTION A-A | DETAILS OF COIL TIE RODS IN BULB TEE GIRDERS | |
(End Diaphragm with Expansion Devices)
Reinforcement:
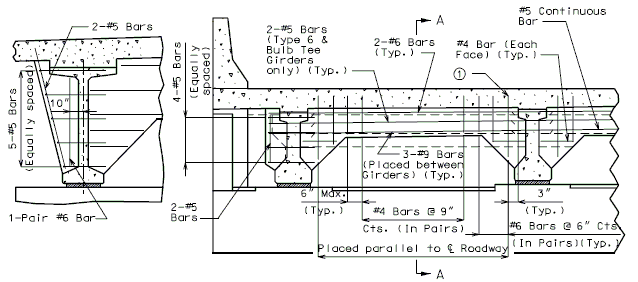
| PART ELEVATION NEAR END BENT FOR BULB TEE GIRDERS |
PART ELEVATION NEAR END BENT |
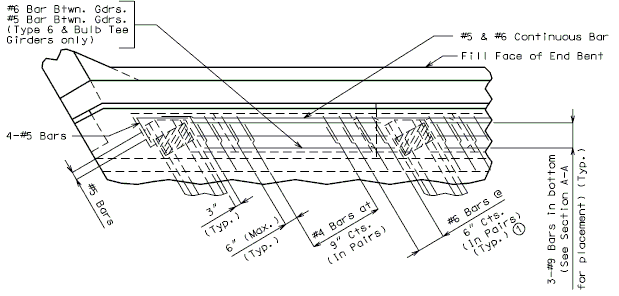
| (1) For Bulb Tee Girders, the first #6 Bar shall be placed 10" from the centerline of Web (Top Flange will prevent some Bars from extending into the Slab). | |
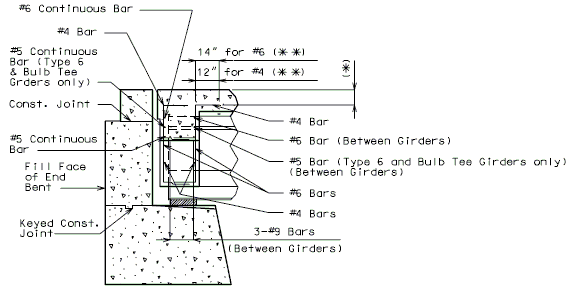
|
|
| NOTE: Epoxy Coat all Reinforcing Steel in the End of Diaphragms.
NOTE: Bars across end of girders to be continuous. | |
| (*) Use the same clearance as longitudinal slab steel. (**) Show this dimension Bridge Plan Sheets. |
- PART SECTION A-A
751.22.3.12 Non-integral Intermediate Bent Diaphragms
(End Diaphragms with Expansion Device)
Dimensions:
- NOTE: Slope at top of Beam Cap and Protective
Coating to be used on Structures with Expansion
Devices.
- NOTE: Slope at top of Beam Cap and Protective
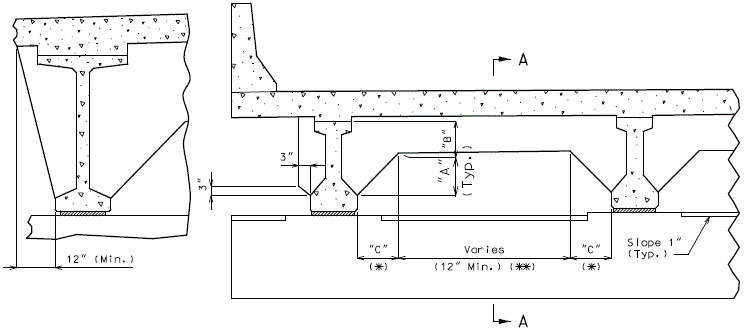
| PART ELEVATION FOR BULB TEE GIRDERS |
PART ELEVATION NEAR INT. BENT |
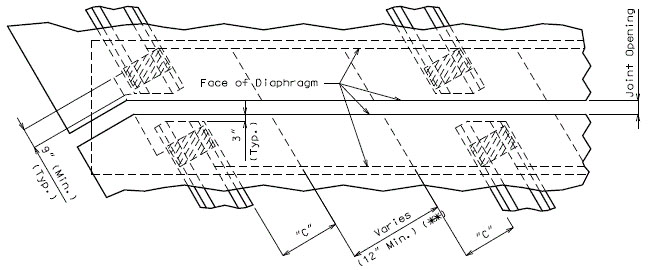
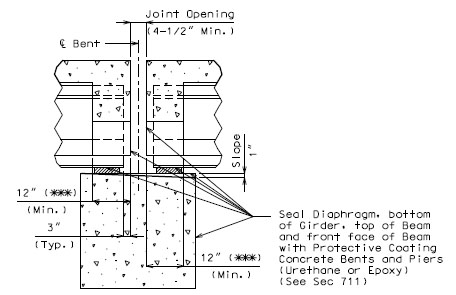 PART SECTION A-A |
(*) A sloped diaphragm allows clearance for the future placement of jacks needed to replace bearings. |
| |||||||||||||||||||||||||||
| (**) For Bulb Tee Girder, spacings less than 8'-8" dimensions "A", "B" & "C" may have to be modified. | |||||||||||||||||||||||||||||
| (***) Make sure the diaphragm is wide enough to provide enough cover for the Coil Tie Rods. | |||||||||||||||||||||||||||||
(End Diaphragms with Expansion Device)
Coil Tie Rods:

| NOTE: | For location of the Coil Tie Rods in a plan view, see Coil Ties. |
| (*) 6" (Min.) shall be used for all I-Girders and Bulb Tee Girders. |
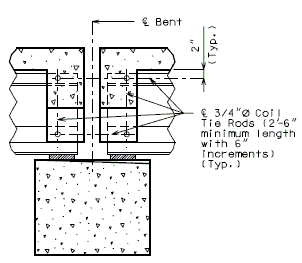
|
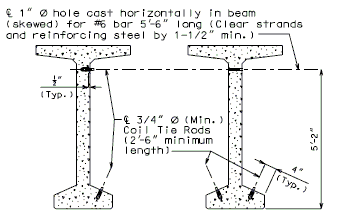
| |
| EXTERIOR GIRDERS | INTERIOR GIRDERS | |
| PART SECTION A-A | DETAILS OF COIL TIE RODS IN BULB TEE GIRDERS | |
(End Diaphragms with Expansion Device)
Reinforcement:
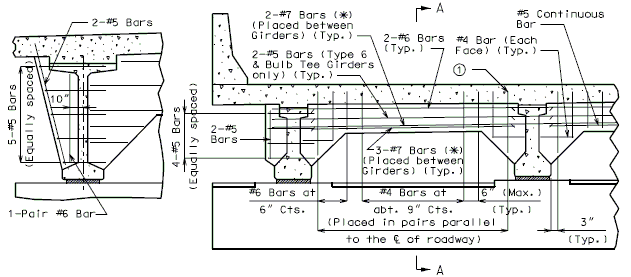
| PART ELEVATION NEAR INT. BENT FOR BULB TEE GIRDERS |
PART ELEVATION NEAR INT. BENT |
- Note: Slope at top of beam cap and protective coating to be used on structures with expansion devices.
- (1) For Bulb Tee Girders, the first #6 Bar shall be placed 10" from the centerline of Web (Top Flange will
prevent some Bars from extending into the Slab).
- (1) For Bulb Tee Girders, the first #6 Bar shall be placed 10" from the centerline of Web (Top Flange will
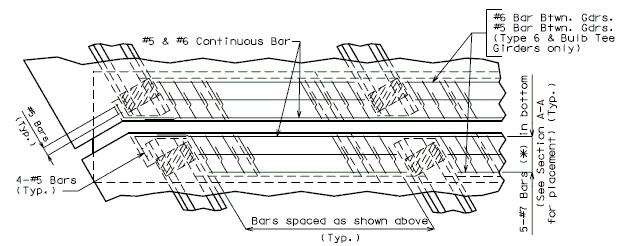
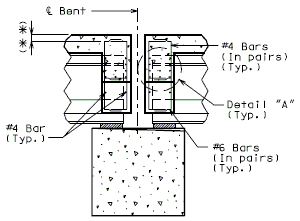
|
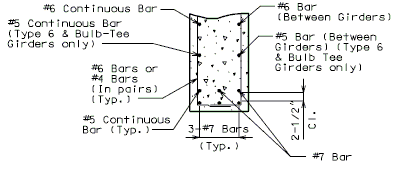
|
| PART SECTION A-A | DETAIL "A" |
| (*) See Detail "A" for the placement of reinforcement.
(**) Use the same clearance as longitudinal slab steel. NOTE: Epoxy coat all reinforcing steel in the end diaphragms. |
(End Diaphragm with Finger Plate Expansion Device)
Diaphragm Reinforcements:
CLOSED DIAPHRAGM:
- (NOTE: Use only when expansion device connects prestress girder series and steel girder series.)
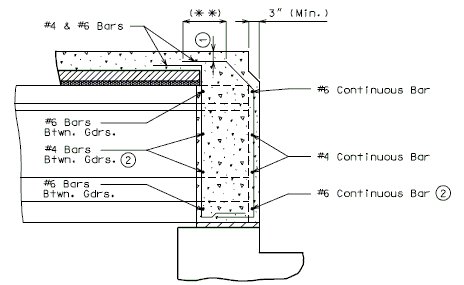
| NOTE: See preceding sheets for bar spacing and detail not shown.
A protective coating shall be applied to concrete surface exposed to drainage from roadway. Indicate surface to be coated on plans. Epoxy coat all reinforcing steel in the end diaphragms. |
(2) For Bulb Tee Girders use 3-#4 Bars in each face. |
OPEN DIAPHRAGM
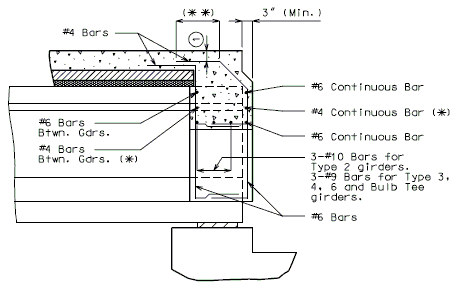
| (*) | Use only on Type 6 Girder | |
| (**) | 12" for #4 Bars 14" for #6 Bars (Shown on Plans) |
(1) Use the same clearance as longitudinal slab steel.
751.22.3.13 Intermediate Diaphragms
(Use Steel Intermediate Diaphragm for Prestress Spans over 50 feet)


| DETAIL "A" | DETAIL "B" |
| (*) | In lieu of 2 1/2" O.D. washers, contractor may substitute a 3/16" (Min. thickness) plate with four 15/16"ø holes and one hardened washer per bolt. |
| (**) | Bolts shall be tightened to provide a tension of one-half that specified in Sec 712 for high strength bolt installation. A325 bolts may be substituted for and installed in accordance with the requirements for the specified A307 bolts. |
| NOTE: | Use Detail "A" at interior girder for diaphragms straight in line across structure. (Use straight diaphragm normal to girders for skews thru 20°).
Use Detail "B" for exterior girder and interior girder for diaphragms stepped across structure. (Use stepped diaphragm for skews over 20°). |

| SECTION C-C | SECTION D-D |

|
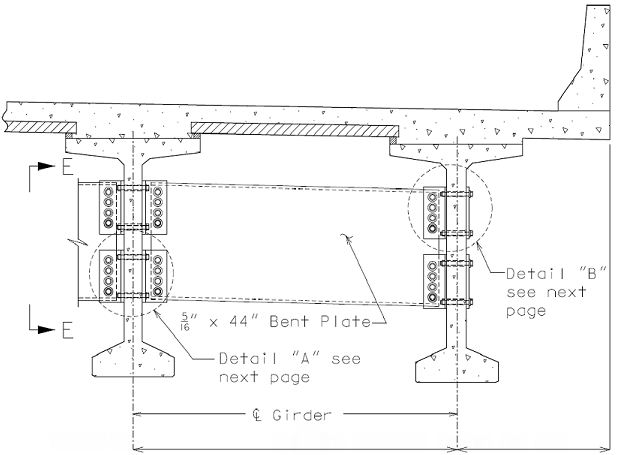
|
| SECTION E-E | |
| PART SECTION SHOWING INTERMEDIATE DIAPHRAGMS (MoDOT Type 7,8, NU 63 and 70) |
Bulb Tee spans of 90 ft. or less require one intermediate diaphragm per span. Bulb Tee spans of over 90 ft. require two intermediate diaphragms per span (spaced equally as allowed by clearance to harped strands). Maximum spacing is 50 ft.
Permanent intermediate diaphragms are not required for NU 35 and NU 43 standard girders. Temporary intermediate diaphragms/bracing are required for construction of the bridge deck. See EPG 751.50 Note H2.98.
The detailer shall check that the 1 1/2 inch ø holes for the diaphragms shown on the design plans will provide a minimum clearance of at least 1 1/2 inches to any prestressing strands.

| DETAIL "A" | DETAIL "B" |
| (*) | In lieu of 2 1/2" O.D. washers, the contractor may substitute a 3/16" (Min. thickness) plate with four 15/16"ø holes and one hardened washer per bolt. |
| (**) | Bolts shall be tightened to provide a tension of one-half that specified in Sec 712 for high strength bolt installation. A325 bolts may be substituted for and installed in accordance with the requirements for the specified A307 bolts. |
| NOTE: | Use Detail "A" at interior girder for diaphragms straight in line across structure. (Use straight diaphragm normal to girders for skews thru 20°).
Use Detail "B" for exterior girder and interior girder for diaphragms stepped across structure. (Use stepped diaphragm for skews over 20°). |

| SECTION C-C | SECTION D-D |
751.22.3.14 Coil Ties

| PART ELEVATION FOR BULB-TEE GIRDERS |
PART ELEVATION |
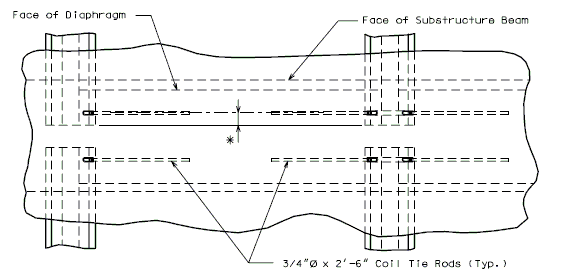
(SQUARE)
* 4" Min. (Typ.) (Do not show Dim. on Plans)
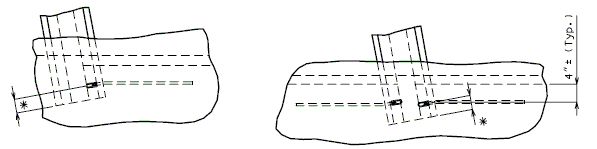
(SKEWED TO 20 DEG.)
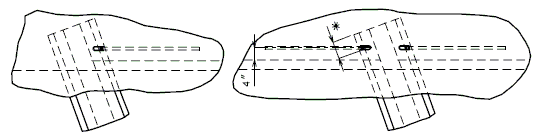
(SKEWED OVER 20 DEG.)
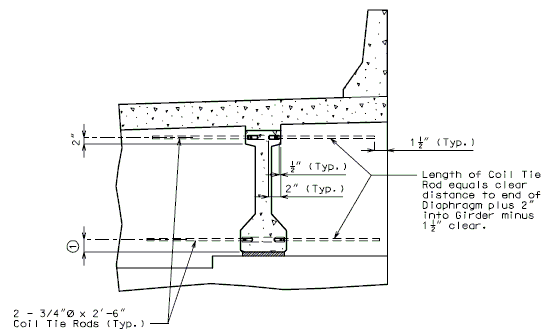
| (1) | 3" For Beam Type 2 5" For Beam Type 3, 4 & 6 |
| NOTE: | See previous page for location of Coil Tie Rods on Bulb Tee girders. |
751.22.3.15 Dowel Bars (Rods)

| PART ELEVATION (FIXED BENT) |
SECTION A-A |
- Dowel bars shall be used for all fixed intermediate bents under prestressed superstructures. Generally, shear resistance from shear key is not considered for typical bridges in seismic performance Category A.
- Dowel bars shall be determined by design. (Minimum #6 Bars @ 12" Cts.) For shear stress, fv, computation, see EPG 751.9.3.1.2 Dowel Rods.
- fv ≤ v ● Fvn
- Where,
- v = Resistance factor
- fv = Shear stress (ksi)
- Fvn = Nominal shear resistance of dowel bar (ksi)
751.22.3.16 Vent Holes
- Note: Use vent holes on all stream crossing structures.
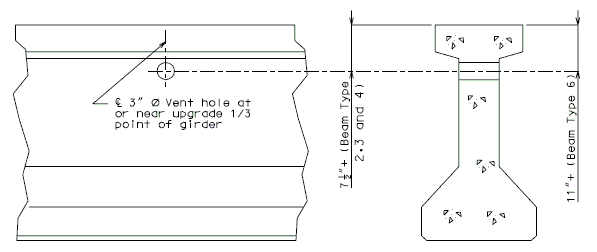
| PART ELEVATION OF GIRDER | PART SECTION NEAR VENT HOLE |
- Note: Place vent holes at or near upgrade of 1/3 point of girders and clear
reinforcing steel or strands by 1-1/2" minimum and steel intermediate
diaphragms bolt connection by 6" minimum.
- Note: Place vent holes at or near upgrade of 1/3 point of girders and clear
751.22.3.17 Shear Blocks
A minimum of two Shear Blocks 12" wide x (1) high by width of diaphragm, will be detailed at effective locations on open diaphragm bent caps when adequate structural restraint cannot be provided for with anchor bolts.
- (1) Height of shear block shall extend a minimum of 1" above the top pf the sole plate.


| Note: Shear blocks shall be used at bents with open diaphragms when anchor bolts can not be designed to resist earthquake loading. |
| Note: For Expansion Bents with open diaphragms, the steps or Shear Block (if applicable) should be normal to the length of cap. |
| Note: For Closed Diaphragm Expansion Bents, the steps or haunches shall be detailed parallel to the centerline of roadway. For Integral End Bents the steps may be skewed due to stirrups being placed parallel to centerline of roadway. Shear Blocks for Expansion Bents with Closed Diaphragms shall be detailed parallel to the centerline of roadway. Shear Blocks used in conjunction with sole plates and anchor bolts shall be detailed parallel to the edge of sole plate. |
751.22.3.18 Miscellaneous
Dimensional Tolerances - I Girders (For Tee Girders & Deck Panels, see Sec 1029)
Note: The following dimensional tolerances will be required (Also see Sec 1027 & 1029)
| Length of beam | ± 1/8 inch per 10 feet of beam length, but not greater than 3/4 inch. |
| Width (flanges, web and fillets) | + 3/8 inch, - 1/4 inch. |
| Depth (flanges, web and fillets) | ± 1/4 inch. |
| Depth (overall) | + 1/2 inch, - 1/4 inch. |
| Horizontal alignment (Deviation from a straight line parallel to centerline of member | 1/2 inch max., to 40-foot lengths. 3/4 inch max., 40 to 60-foot lengths. 1 inch max., 60-foot or greater lengths. |
| Camber (Deviation from design camber within 7 days of strand release) | ± 1/2 inch, to 80-foot lengths. ± 1 inch, greater than 80-foot lengths. |
| Stirrup bars (projection above top of beam) | ± 3/4 inch. |
| Stirrup bars (longitudinal spacing) | ± 2 inches |
| Tendon position | ± 1/4 inch center of gravity of strand group and individual tendons. |
| Position of deflection points for deflected strands | ± 6 inches, longitudinal. |
| Position for lifting devices | ± 6 inches, longitudinal. |
| Side Inserts (Centerline to centerline and centerline to end) | ± 1/2 inch. |
| Coil Inserts (Centerline to centerline and centerline to end) | ± 2 inches horizontal, except must be 3 inches or more from end of beam and within reinforcement cage of bent, ± 1 inch vertical. |
| Slab Drain Inserts | ± 1/2 inch from designated location, engineer may approve location ± 6 inches from design, multiple inserts for single drain must be within ± 1/2 inch of vertical line. |
| Exposed beam ends (deviation from square or designated skew) | ± 1/4 inch horizontal, ± 1/8 inch vertical per foot of beam height. |
| Bearing area (deviation from plane) | ± 1/8 inch. |
| Bearing plates (centerline to centerline) | ± 1/8 inch per 10 feet of beam length, but not greater than 3/4 inch. |
| Bearing plates (centerline to end of beam) | ± 1/2 inch. |
| Diaphragm Hole Location | ± 1 1/2 inches for centerline of group ± 1/2 inch within group. |
Expansion Device Support Slots
Used with preformed compression joint seal, flat plate, strip seal or finger plate expansion devices.
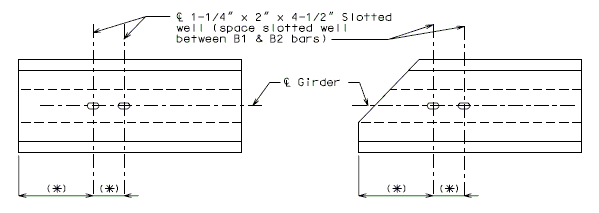
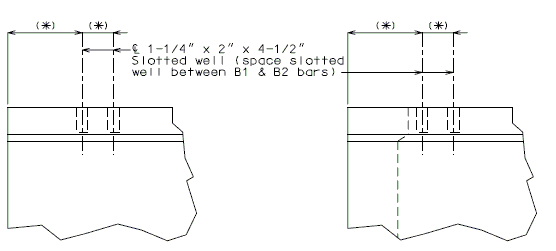
Anchor Bolts
Simple Spans
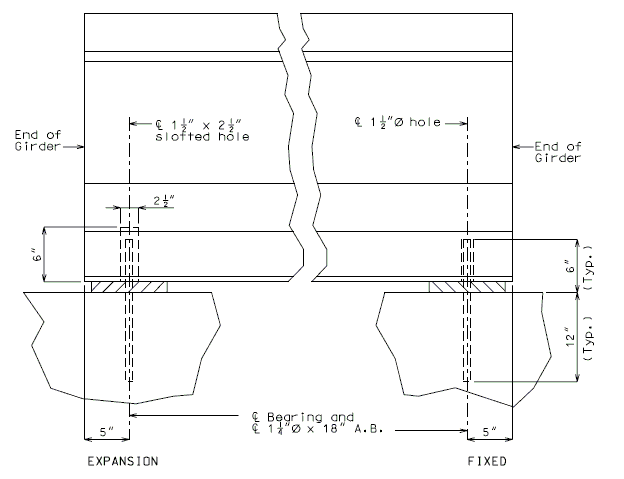
| Note:
It is permissible for the reinforcing bars and or the strands to come in contact with the materials used in forming A.B. holes. If A.B. holes are formed with galvanized sheet metal, the forms may be left in place. Hole (1-1/2"ø) to be grouted with expansive type mortar meeting the requirements of Sec 1066. |