751.40 LFD Widening and Repair (CONTINUED)
751.40.8.11 Open Concrete Intermediate Bents and Piers
751.40.8.11.1 Design
751.40.8.11.1.1 General and Unit Stresses
GENERAL
Use Load Factor design method, except for footing pressure and pile capacity where the Service Load design method shall be used.
In some cases, Service Load design method may be permitted on widening projects, see Structural Project Manager.
The terms, Intermediate Bents and Piers, are to be considered interchangeable for EPG 751.40.8.11 Open Concrete Intermediate Bents and Piers.
DESIGN UNIT STRESSES
(1) Reinforced Concrete
Class B Concrete (Substructure) = 1,200 psi = 3,000 psi Reinforcing Steel (Grade 60) = 24,000 psi = 60,000 psi n = 10 (AASHTO Article 8.7.1) (*)
(2) Reinforced Concrete (**)
Class B-1 Concrete (Substructure) = 1,600 psi = 4,000 psi Reinforcing Steel (Grade 60) = 24,000 psi = 60,000 psi = 8 (AASHTO Article 8.7.1) (*)
(3) Structural Steel
- Structural Carbon Steel (ASTM A709 Grade 36)
- = 20,000 psi, = 36,000 psi
(4) Overstress
- The allowable overstresses as specified in AASHTO Article 3.22 shall be used where applicable for Service Load design method.
(*) Use
(**) May be used for special cases, see Structural Project Manager.
751.40.8.11.1.2 Loads
(1) Dead Loads
(2) Live Loads
- As specified on the Bridge Memorandum.
- Impact of 30% is to be used for the design of beam, web supporting beam and top of columns. No impact is to be used for bottom of column, tie beam or footing design.
(3) Wind and Frictional Forces
(4) Temperature and Shrinkage
- The effect of normal and parallel components to the bent shall be considered. When bearings with high friction coefficients are used or for long bridge lengths, the columns and footings are to be analyzed for moments normal to the bent due to the horizontal deflection of the top of the bent.
(5) Buoyancy
- If specified by the Structural Project Manager, or by the Bridge Memorandum.
(6) Earth Pressure
- Bents are to be analyzed for moments due to equivalent fluid pressure on columns and web where the ground line at time of construction, or potential changes in the ground line, indicate.
(7) Earthquake
- See Structural Project Manager or Liaison.
(8) Special Stability Situations
- When indicated by the Bridge Memorandum or by the Structural Project Manager, piers must be analyzed for special loadings as directed (i.e., differential settlement).
(9) Collision
- Where the possibility of collision exists from railroad traffic, the appropriate protection system, for example Collision Wall, shall be provided (See the Bridge Memorandum).
(10) Collision Walls
- Collision walls are to be designed for the unequal horizontal forces from the earth pressure, if the condition exists (See the Bridge Memorandum). The vertical force on the collision wall is the dead load weight of the wall (*). If a bent has three or more columns, design the steel in the top of the wall for negative moment.
(*) For footing design, the eccentricity dead load moment due to an unsymmetrical collision wall shall be considered.
751.40.8.11.1.3 Distribution of Loads
(1) Dead Loads
- Loads from stringers, girders, etc. shall be concentrated loads applied at the centerline of bearing. Loads from superstructure, such as concrete slab spans, shall be applied as uniformly distributed loads.
(2) Live Loads
- Loads from stringers, girders, etc., shall be applied as concentrated loads at the intersection of centerline of stringer and centerline of bent.
(3) Wind and Frictional Forces
(4) Temperature
- Apply at the top of the substructure beam.
(5) Earth Loads
- (a) Vertical
- Vertical earth loads on tie beams shall be applied as uniform loads for a column of earth equal to 3 times the width of the beam. The weight of earth for footing design shall be that directly above the footing, excluding that occupied by the column.
- The earth above the seal courses shall be considered in computing pile loads. Refer to the Design and Dimension of the Pile Footings portion of EPG 751.40.8.13 Concrete Pile Cap Non-Integral End Bents or EPG 751.36 Driven Piles.
- (b) Horizontal
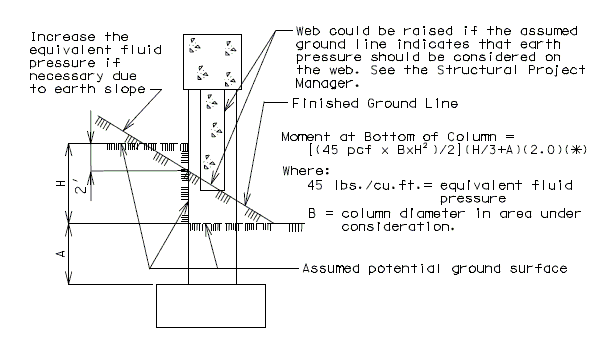
(*) A factor of 2.0 is applied to the moment to allow for the possibility of the column esisting earth pressure caused by the earth behind the column twice the column width.
(6) Earthquake Loads
- See Structural Project Manager or Liaison.
(7) Seal Course
- The weight of the seal course shall not be considered as contributing to the pile loads, except for unusual cases.
751.40.8.11.1.4 Types of Design
TYPES OF DESIGN
Rigid frame design is to be used for the design of Intermediate Bents and Piers.
The joint between the beam and column, and web or tie beam and column, is assumed to be integral for all phases of design and must be analyzed for reinforcement requirements as a "Rigid Frame".
The joint between the column and footing is assumed to be "fixed", unless foundation fexibility needs to be considered (consult Structural Project Manager for this assessment).
If the distance from the ground line to the footing is large (*), consideration shall be given to assuming the column to be "fixed" at a point below the ground line.
(*) When the distance from the ground line to the top of footing is 10' or more, the unsupported height and the fixed point may be measured from the bottom of the beam to the ground line plus 1/2 of the distance from the ground line to the top of the footing.
UNSUPPORTED HEIGHT
Unsupported height is the distance from the bottom of the beam to the top of the footing.
SINGLE COLUMN
Use rigid frame design with the column considered "fixed" at the bottom for all of the conditions.
COLUMN DIAMETER CHANGE
Use a change in column diameter as required by the Bridge Memorandum or column design.
COLUMN SPACING (TRIAL)
(Except Web Supporting Beam type)
Estimate centerline-centerline column spacing for a two column bent as 72% of the distance from the centerline of the outside girder to the centerline of the outside girder.
A three column bent spacing estimation is 44% of the centerline-centerline outside girder spacing.
751.40.8.11.2 Reinforcement
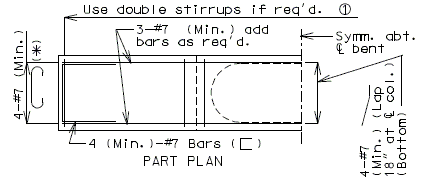
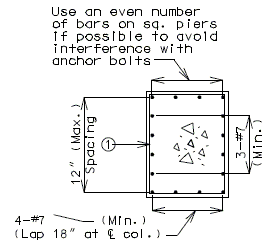
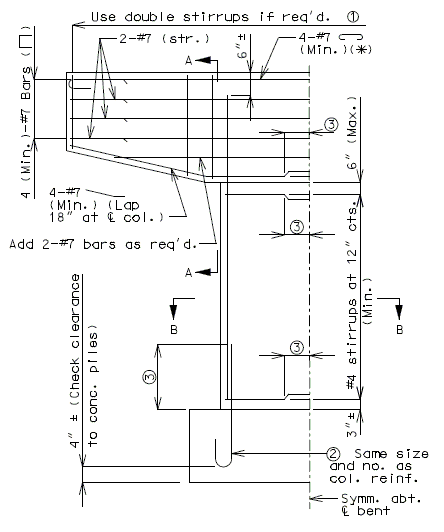
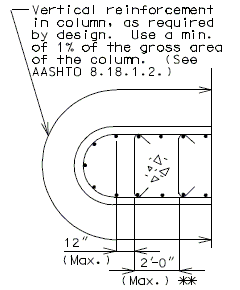
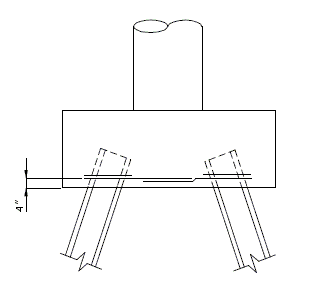
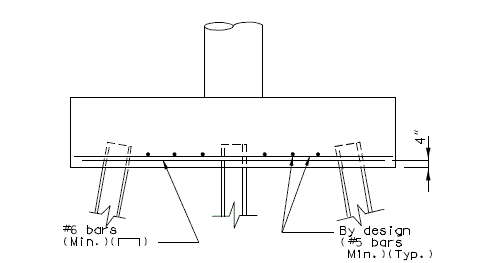
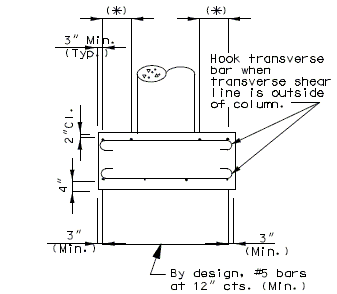
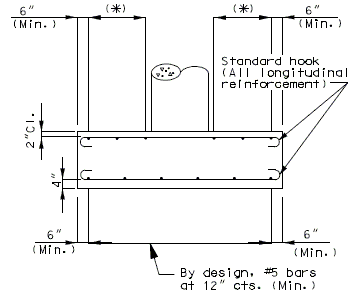
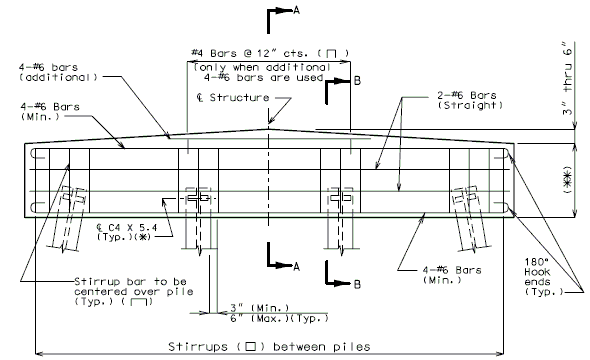
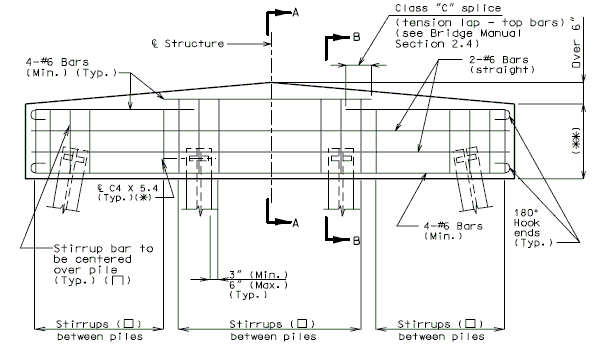
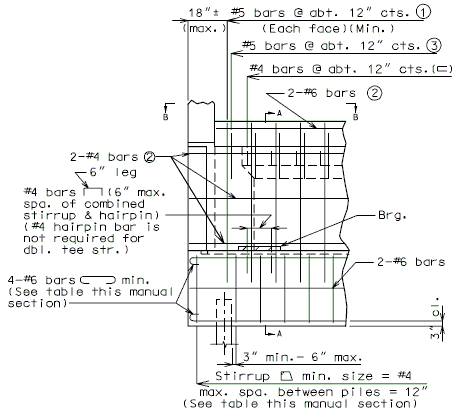
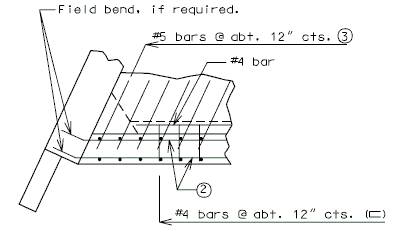
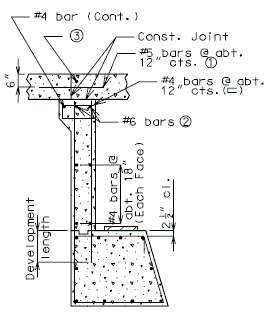
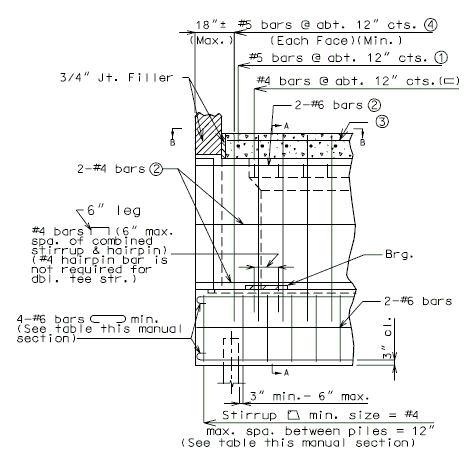
751.40.8.11.2.1 Hammer Head Type
(*) Add hooked reinforcement as required by design.
(**) See AASHTO Article 8.18.2.3.4 for tie requirements.
![]() All stirrups in beam to be the same size bar. (Use a min. spacing of 5" (6" for double stirrups), minimum stirrups are #4 at 12" cts., and maximum
stirrups are #6 at 6" cts.)
All stirrups in beam to be the same size bar. (Use a min. spacing of 5" (6" for double stirrups), minimum stirrups are #4 at 12" cts., and maximum
stirrups are #6 at 6" cts.)
Locate #4 bars (┌─┐) under bearings if required. (Not required for P/S Double-Tee Girders.)
![]() See development length (Other than top bars) or standard hooks in
tension, Ldh.
See development length (Other than top bars) or standard hooks in
tension, Ldh.
751.40.8.11.3 Pile Footings
751.40.8.11.3.1 Design and Dimensions
GENERAL
- Number, size and spacing of piling shall be determined by computing the pile loads and applying the proper allowable overstresses.
- Cases of Loading: (AASHTO Article 3.22)
- Group I and Group II maximum vertical loads (refer to distribution of loads, this Section).
- Group III thru VI wind and/or temperature moments with applicable vertical loads.
- Internal stresses including the position of the shear line shall then be computed.
- Long narrow footings are not desirable and care should be taken to avoid the use of an extremely long footing 6~0" wide when a shorter footing 8'-3" or 9'-0" wide could be used.
- Footings are to be designed for the greater of the minimum moment requirements at the bottom of the column, or the moments at the bottom of the footing.
- When using the load factor design method for footings, design the number of piles needed based on the working stress design method.
PILE LOADS
- Pile Loads - Vertical Loads - Number of Piles - Overturning Moment If minimum eccentricity controls the moment in both directions, It is necessary to use the moment in one direction (direction with less section modulus of pile group) only for the footing check. - Section Modulus of Pile Group
- (A) AASHTO Group I thru VI Loads as applicable
- Maximum = Pile Capacity
- Minimum (zero)
- Tension on a pile will not be allowed for any combination of forces.
- Pile design force shall be calculated with consideration of AASHTO percentage overstress factors.
- (B) Earthquake Loads
See Structural Project Manager or Liaison before using the following seismic information.
- Point Bearing Pile
- Maximum (**)
- (i.e., for HP 10 X 42 piles, Max. tons/pile)
- Minimum = Allowable uplift force specified for piles in this
- Section under Seal Course Design.
- (**) Two "2" is our normal factor of safety. Under earthquake loadings only the point bearing pile and rock capacities are their ultimate capacities.
- Friction Piles
- Maximum = Pile Capacity
- Minimum = Allowable uplift force specified for piles in this
- Section under Seal Course Design.
- See combined axial & bending stresses in Cast-In-Place friction piles in liquefaction areas.
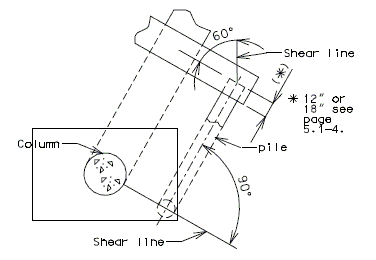
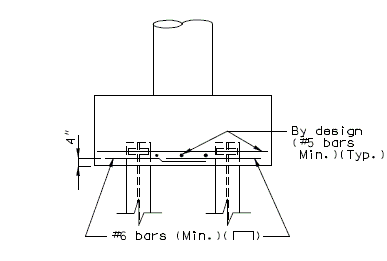
(1) Shear Line
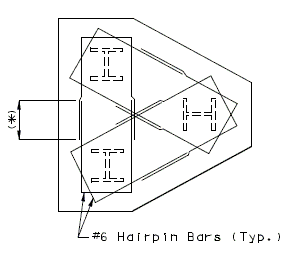
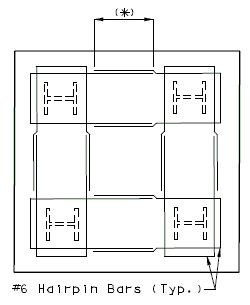
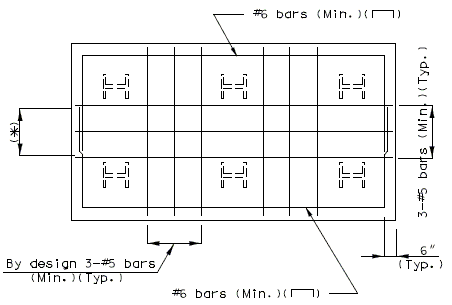
| If the shear line is within the column projected, the footing may be considered satisfactory for all conditions and standard #6 hairpin bars shall be used.
|
|
(2) Bending
The critical section for bending shall be taken at the face of the columns (concentric square of equivalent area for round columns).
The reinforcement shall be as indicated for reinforced footings, except that the standard #6 hairpin bars may be used for small footings if they provide sufficient steel area.
(3) Distribution of Reinforcement
Reinforcement in Bottom of Footing
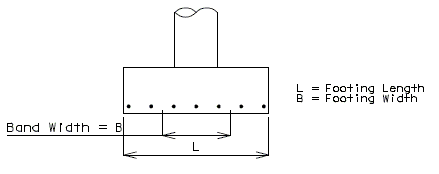
Reinforcement shall be distributed uniformly across the entire width of footing in the long direction. In the short direction, the portion of the total reinforcement given by AASHTO Equation 4.4.11.2.2-1 shall be distributed uniformly over a band width equal to the length of the short side of the footing, .
- Band Width Reinforcement =
- where
The remainder of the reinforcement required in the short direction shall be distributed uniformly outside the center band width of footing.
Reinforcement in Top of Footing
Reinforcement in the top of the footing shall be provided based on a seismic analysis for Seismic Performance Categories B, C and D. This reinforcement shall be at least the equivalent area as the bottom steel in both directions. The top steel shall be placed uniformly outside the column.
(4) Shear
(AASHTO Article 8.15.5 or 8.16.6)
The shear capacity of footing in the vicinity of concentrated loads shall be governed by the more severe of the following two conditions.
(i) Beam shear
Critical Section at "d" distance from face of column.
| b = Footing Width Service Load | 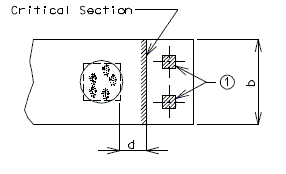
|
| Service Load | |
| Load Factor | |
| PART PLAN OF FOOTING |
|---|
(ii)Peripheral Shear
Critical Section at "d/2" distance from face of column.
| Service Load | 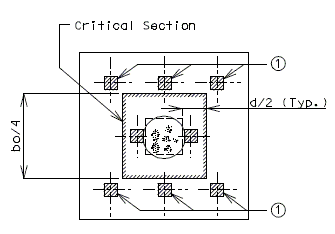
|
| Load Factor | |
| PART PLAN OF FOOTING |
|---|
If shear stress is excessive, increase footing depth.
| Piles to be considered for shear. (Center of piles are at or outside the critical section.) |
 |
|
| SIDE ELEVATION | FRONT ELEVATION |
|---|
TYPICAL PLAN OF
3 PILE FOOTINGS
(minimum pile spacings)
NOTES:
Use 3- piles on exterior foorings only.
Use only HP 10 x 42 or friction piles on three pile footings.
TYPICAL PLAN
STAGGERED PILE
(7 Pile footings shall not be used.)
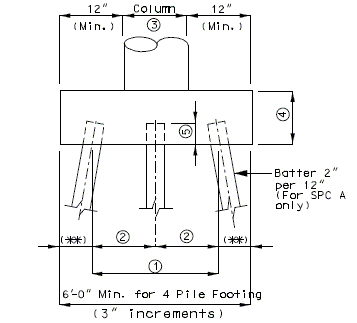
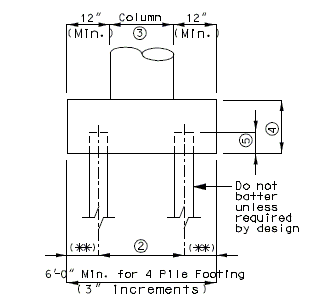
| If horizontal thrust requires pile batter- consult the Structural Project Manager. |
(*) The maximum pile spacing is 4'-0".
751.40.8.11.3.2 Reinforcement
Unreinforced Footing - Use only in Seismic Performance Category A
|
|
| Elevation (3 Pile Footing) |
Elevation (4 Pile Footing |
|---|---|
|
|
| Plan (3 Pile Footing) |
Plan (4 Pile Footing |
| (*) | See lap splice class C (Other than top bars). |
| Notes: | Reiforcement not required by design. Hairpins are sufficient for renforcing requirements. |
| The minimum percentage of reinforcement, "P" , is not required to be met, unless scour is anticipated. | |
| Use for all types of piling, except timber. |
Reinforced Footing - Seismic Performance Category A
|
|
| Front Elevation | Side Elevation |
|---|---|
| |
| Plan | |
| (*) | See lap splice class C (Other than top bars). |
| Note: | The maximum size of stress steel allowed is #8 bars. |
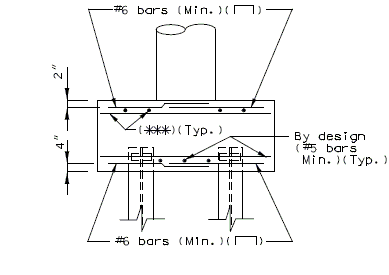
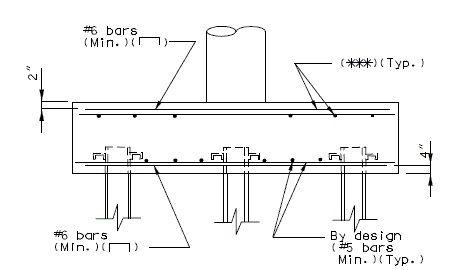
Reinforced Footing - Seismic Performance Categorys B, C & D
See Structural Project Manager or Liaison before using the following seismic details.
|
|
| Front Elevation | Side Elevation |
|---|---|
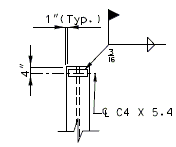
|
|
| Typical Detail Pile Channel Shear Connector | |
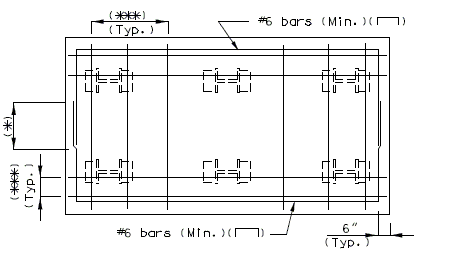
| Plan Showing Top Reinforcement | |
| |
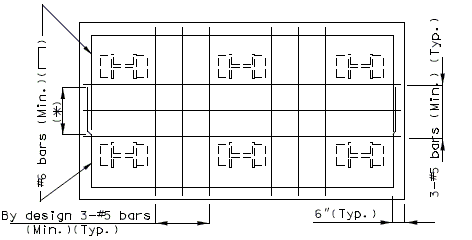
| Plan Showing Bottom reinforcement | |
| (*) | For reinforcement in top of the footing, see lap splice class C (Top bars). |
| (**) | Place the top reinforcement uniformly outside the column. |
| (***) | Use same area of steel in the top of the footing as is required for the bottom. |
| Notes: | For reinforcement in bottom of the footing, see lap splice Class C (Other than top bars). |
| The maximum size of stress steel allowed is #8 bars. | |
| Unreinforced footings shall not be used in seismic performance categories B, C & D. |
751.40.8.11.4 Spread Footings
751.40.8.11.4.1 Design and Dimensions
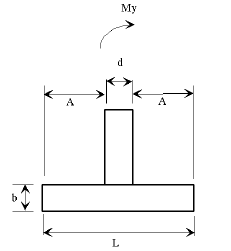
|
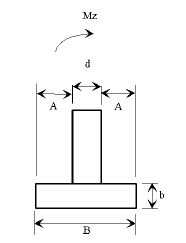
|
| Side Elevation | Front Elevation |
|---|
| d | = column diameter |
| L | = footing length |
| b | = footing depth |
| B | = footing width |
| A | = edge distance from column |
The calculated bearing pressure shall be less than the ultimate capacity of the foundation soil. The ultimate capacity of the foundation soil can be conservatively estimated as 2.0 times the allowable bearing pressure given on the Bridge Memorandum. The analysis method of calculating bearing pressures is outlined in the following information.
Dimensional Requirements
| L - | Minimum of 1/6 x distance from top of beam to bottom of footing (3" increments); |
| B - | Minimum footing width is column diameter + 2A, (3" increments); |
| A - | Minimum of 12"; |
| b - | Minimum of 30" or column diameter, Maximum of 72" at 3" increments; (for column diameters 48" and greater use a 48" minimum footing depth.) |
Size
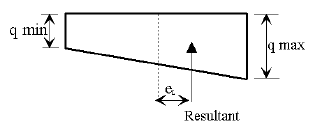
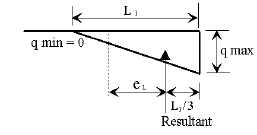
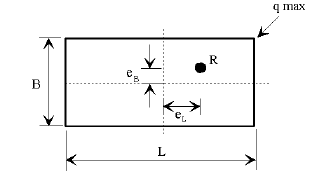
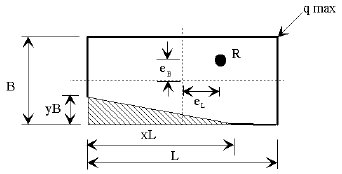
The size of footing shall be determined by computing the location of the resultant force and by calculating the bearing pressure.
Long, narrow footings are to be avoided, especially on foundation material of low capacity. In general, the length to width ratio should not exceed 2.0, except on structures where the ratio of the longitudinal to transverse loads or some other consideration makes the use of such a ratio limit impractical.
Location of Resultant Force
The location of the resultant force shall be determined by the following equations.
The Middle 1/3 is defined as:
The Middle 1/2 is defined as: and
The Middle 2/3 is defined as: and
The following table specifies requirements for the location of the resultant force.
| Soil Type | Resultant Location Group I - VI | Resultant Location Earthquake Loads Categories B, C and D |
|---|---|---|
| Clay, clay and boulders, cemented gravel, soft shale with allowable bearing values less than 6 tons, etc. | middle 1/3 | middle 1/2 |
| Rock, hard shale with allowable bearing values of 6 tons or more. | middle 1/2 | middle 2/3 |
Bearing Pressure
The bearing pressure for Group I thru VI loads shall be calculated using service loads and the allowable overstress reduction factors as specified in AASHTO Table 3.21.1A. The calculated bearing pressure shall be less than the allowable pressure given on the Bridge Memorandum.
The bearing pressure for Earthquake Loads in Categories B, C, and D shall be calculated from loads specified in AASHTO Division I-A Seismic Design, Sections 6.2.2, 7.2.1, and 7.2.2. The seismic design moment shall be the elastic seismic moment (EQ) divided by the modified response modification factor R'. The modified seismic moment shall then be combined independently with moments from other loads:
Group Load =
Where:
| = dead load | |
| = buoyancy | |
| = stream flow pressure | |
| = elastic seismic moment | |
| = earth pressure | |
| = R/2 for category B | |
| = 1 for categories C and D | |
| = Response Modification Factor | |
| = 5 for multi-column bent | |
| = 3 for single-column bent | |
The calculated bearing pressure shall be less than the ultimate capacity of the foundation soil. The ultimate capacity of the foundation soil can be conservatively estimated as 2.0 times the allowable bearing pressure given on the Bridge Memorandum. The analysis method of calculating bearing pressures is outlined in the following information.
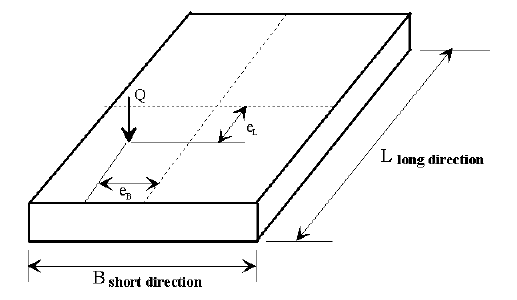
| For | For |
|---|---|
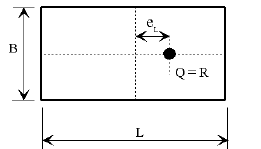
|
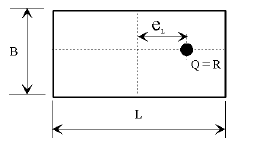
|
| Plan View | Plan View |
|
|
| Bearing Pressure | Bearing Pressure |
| CASE 1 | CASE 2 | |
|---|---|---|
|
| |
| k, x and y from AASHTO chart | ||
| CASE 1 Plan View | CASE 2 Plan View | |
| CASE 3 | CASE 4 | |
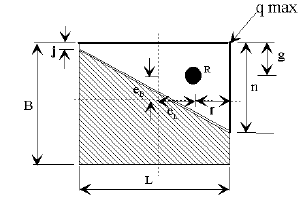
|
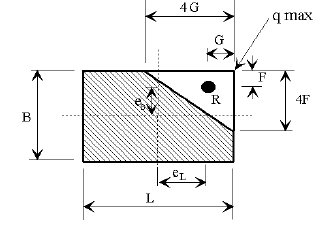
| |
| CASE 3 Plan View | CASE 4 Plan View | |
Loading Cases
Loads for Groups I thru VI shall be calculated for all bridges.
Earthquake loads shall be calculated when the bridge is in Seismic Zones B, C, and D.
Loads for other group loadings shall be used on a case by case basis.
Reinforcement
The footing is to be designed so that the shear strength of the concrete is adequate to handle the shear stress without the additional help of reinforcement. If the shear stress is too great, the footing depth should be increased.
Shear
The shear capacity of the footings in the vicinity of concentrated loads shall be governed by the more severe of the following two conditions.
Critical section at "d" distance from face of column:
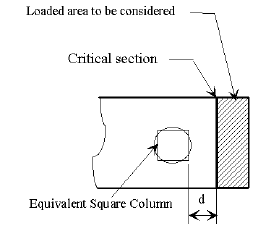
|
| Load Factor |
|---|
| = footing width |
Critical section at "d/2" distance from face of column:
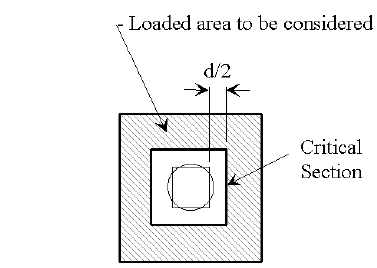
|
| Load Factor |
|---|
| If shear stress is excessive, increase footing depth. | |
Bending
If the shear line is within the projected equivalent square column, the footing may be considered satisfactory for all conditions. (minimum reinforcement required)
If the shear line is outside of the projected column, the footing must be analyzed and reinforced for bending and checked for shear stress.
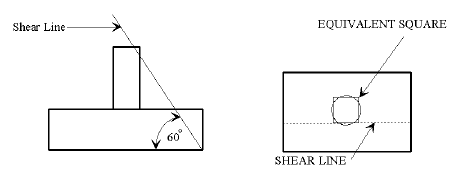
The critical section for bending shall be taken at the face of the equivalent square column. The equivalent square column is the theoretical square column which has a cross sectional area equal to the round section of the actual column and placed concentrically.
Reinforcement in Bottom of Footing
The bearing pressure used to design bending reinforcement for Group I thru VI loads shall be calculated using Load Factor Loads.
The bearing pressure used to design bending reinforcement for Earthquake Loads in Categories B, C, and D shall be calculated from the same loads as specified in AASHTO Division 1-A Seismic Design for ultimate bearing pressure.
The bottom reinforcement shall be designed using ultimate strength design.
Distribution of Reinforcement
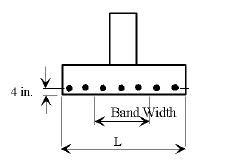
|
| L = Footing Length |
| B = Footing Width |
Reinforcement shall be distributed uniformly across the entire width of footing in the long direction. In the short direction, the portion of the total reinforcement given by AASHTO Equation 4.4.11.2.2-1 shall be distributed uniformly over a band width equal to the length of the short side of the footing, B.
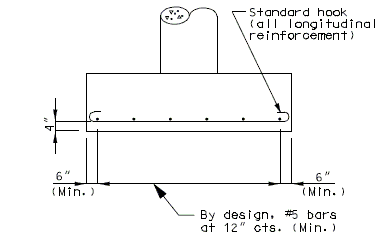
Reinforcement in Top of Footing
Reinforcement in the top of the footing shall be provided for Seismic Performance Categories B, C, and D. This reinforcement shall be the equivalent area as the bottom steel in both directions. The top steel shall be placed uniformly outside the column.
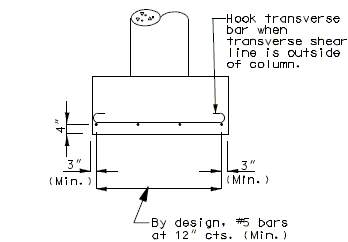
|
|
| Front Elevation | Side Elevation |
|---|
|
|
| Front Elevation | Side Elevation |
|---|
| (*) | Use same area of steel in the top of the footing as is required for the bottom. |
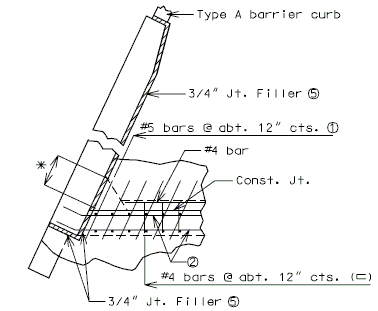
751.40.8.11.5 T- Joint Connections
Principal Tension and Compression Stresses in Beam-Column Joints
The connections where columns and beams join, or where columns and footings join, should be based on the capacity design for shear and diagonal tension. For most locations, this is a “T”-shaped joint. For the analysis of “knee joints”, see Priestley and Seible, 1996.

In the capacity design of connection joints, the column moment, M0, will be the moment that is known and which will correspond to flexural overstrength of the column plastic hinges, i.e. M0 = 1.3Mp of the column. If the columns are designed based on plastic hinging, the beam and footings shall be designed with capacities greater than or equal to 1.3Mp.
At each joint, the principal tension and compression stresses are defined and checked as follows:
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
- (7)
- (8)
- in which:
- Vjh = Average horizontal shear force within a joint.
- Vjv = Average vertical shear force within a joint.
- vjh = Average horizontal shear stress within a joint.
- vjv = Average vertical shear stress within a joint.
- hb = Beam depth.
- hc = Column diameter or rectangular column cross-section height.
- bje = The effective width of a joint, defined in Fig. 751.40.8.11.5.2.
- D = Round column diameter.
- fv = Average vertical axial stress due to column axial force Pc, including the seismic component.
- Pc = Column axial force.
- fh = Average horizontal axial stress at the center of the joint.
- pc = Nominal principal compression stress in a joint. (positive)
- pt = Nominal principal tensile stress in a joint. (negative)
- bb = Beam width
- bc = Column cross-section width
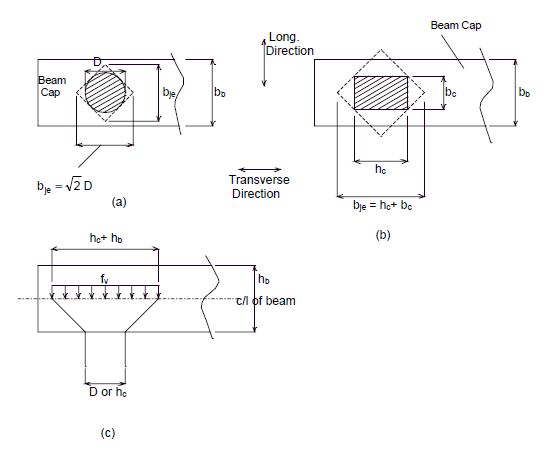
In Fig. 751.40.8.11.5.2(c), the effective width is taken at the center of the column section, allowing a 45° spread from boundaries of the column section into the beam cap. In the transverse direction, the effective width will be the smaller of the value given by eq. (3) and the beam cap width bb. Experimental evidence indicates that diagonal cracking is initiated in the joint region when psi. The principle compression stress pc shall be limited to .
Design of Reinforcement for Beam-Column Joints
When the principal tension stress, pt, exceeds psi, joint cracking occurs and the following reinforcement shall be provided:
a) Vertical beam stirrup reinforcement shall be placed throughout the distance of hb/2 from the column face on each side of the column. The required amount of vertical beam stirrup reinforcement, Ajv, is:
- (9)
- Where:
- Asc = The total area of longitudinal steel
- f°yc = overstrength stress in the column reinforcement use
- f°yc = 1.1f
- fyv = yield stress of vertical stirrup reinforcement.
b) Vertical beam stirrup reinforcement within the joint, Avi, is
- (10)
c) The additional beam bottom longitudinal reinforcement required is
- (11)
- where fyb = the yield stress of the beam bottom longitudinal reinforcement. This additional reinforcement must be carried a sufficient distance to develop its yield strength a distance hb/2 from the column face.
d) The horizontal hoop reinforcement within a joint requires
- (12)
which for F = 0 simplifies to
- (13)
- Where
- F = The beam cap prestress force.
- fyh = The yield stress of the horizontal hoops.
- La = The Anchorage length in the joint.
The minimum amount of horizontal hoop reinforcement shall be
- (14)
The spacing of the horizontal hoop can be based on:
(15)
- Where
- As = The cross-sectional area of the hoop bar.
- D’ = The hoop diameter.
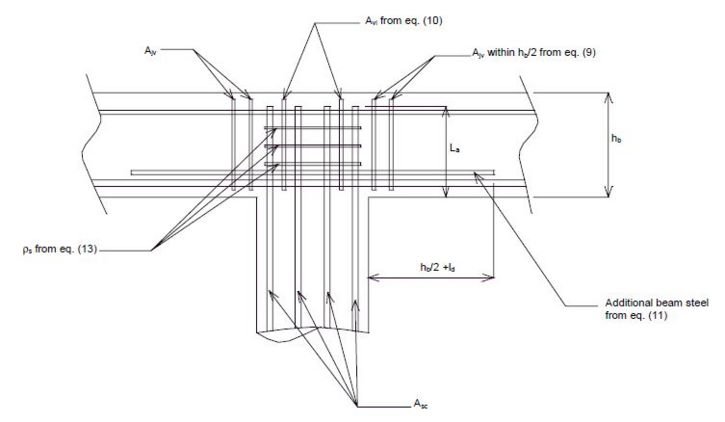
When the principal tension stress, pt, does not exceed psi, no joint cracking is expected. However, the following minimum reinforcement shall be provided:
- a) Vertical beam stirrup reinforcement within the joint based on eq. (10)
- b) Minimum horizontal hoop reinforcement based on eq. (14)
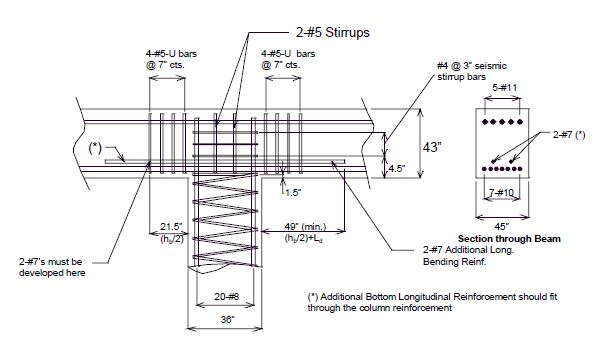
Note that the bending of any hooked reinforcement outward, away from the column core, shall not be used because it directs the anchorage force away from the joint. Inward bending of the column reinforcement is allowed. However, it is likely to cause a congestion problem. The use of straight column reinforcement embedded into the beam-column joint is recommended. The standard T-joint reinforcement details are shown in Figs. 751.40.8.11.5.4 - 751.40.8.11.5.6. If any reinforcement requirement based on eqs. (9) through (14) is greater than that shown in Figs. 751.40.8.11.5.4 - 751.40.8.11.5.6, the greater requirement shall be used.
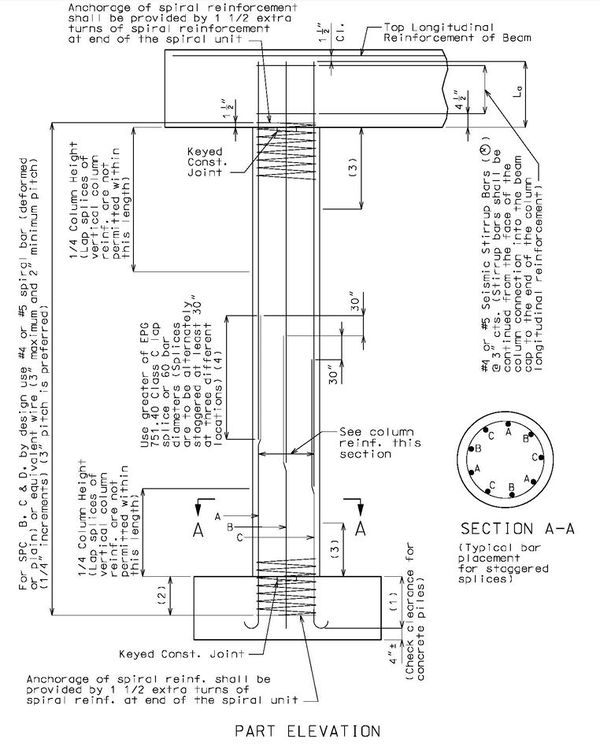
- (1) Increase by 25% the development length (other than top bars) or the standard hook in tension “Ldh” of EPG 751.40.8.4.2.
- (2) The spiral bars or wire shall be continued for a distance equal to ½ the column diameter but not less than 15” from the face of the column connection into the footing.
- (3) Use the greatest length of the following: column diameter of 1/6 of the clear height of column. Lapping of spiral reinforcement in this region is not permitted.
- (4) Splices may be eliminated when the column height is 20’-0” or less or restrictions do not practically allow for lap splices.
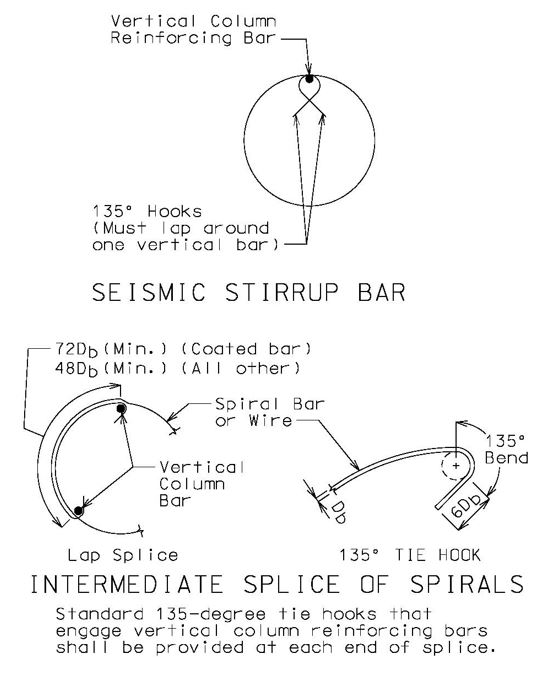
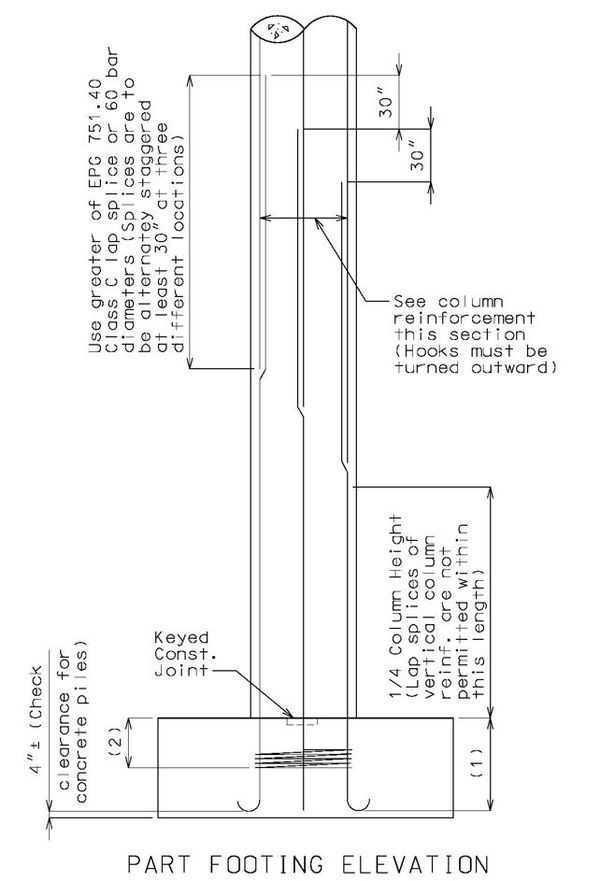
- See additional guidance in EPG 751.9.3.1.7, below, for footing reinforcement not shown.
- (1) Increase by 25% the development length (other than top bars) or the standard hook minimum in tension “Ldh” of EPG 751.40.8.4.2.
- (2) The spirals shall be continued for a distance equal to ½ the column diameter but not less than 15” from the face of the column connection into the footing.
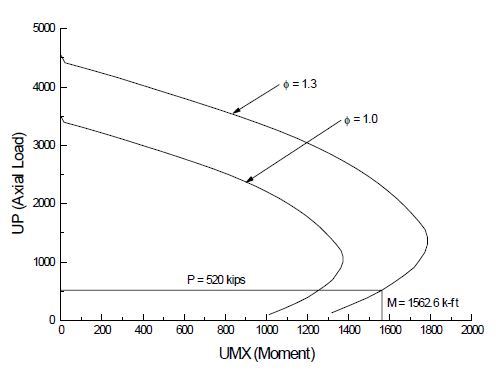
Example 751.40.8.11.5.1: A column is subjected to an axial load (due to dead and seismic earthquake loads) of 520 kips. The column diameter is 36 in. with 20 #8 bars for longitudinal reinforcement. The beam cap dimensions are 3 ft. 9 in. wide by 3 ft. 7 in. deep with 5 #11 bars for the top reinforcement and 7 #10 bars for the bottom reinforcement as shown in Fig. 751.40.8.11.5.7. The column overstrength moment-axial load curve is shown in Fig. 751.40.8.11.5.8. Design the reinforcement details for the beam-column joint.
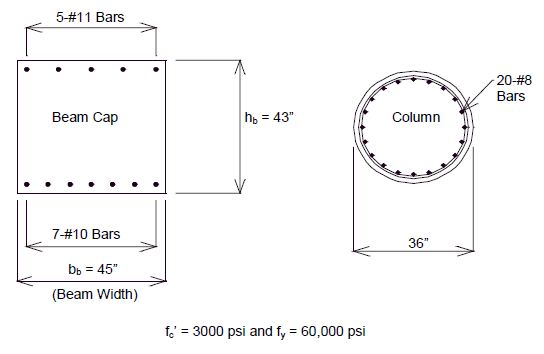
Solution:
The axial load for the column = 520 kips.
From Fig. 751.40.8.11.5.8, M0 = 1562.6 k-ft.
From eq. (1): = 436.07 kips
From eq. (3): = 45 in.
From eq. (2): = 269.18 psi.
Vertical Axial Stress:
From eq. (6):
- = 146.27 psi.
Horizontal Stress:
- fh = 0 psi.
From eq. (7):
pc = 352.07 psi ≤ 0.3(3000 psi) = 900 psi O.K.
From eq. (8):
pt = -205.80 psi ≥ 3.5 3000 = 191.7 psi Not O.K.
Since pt is greater than , special joint reinforcement based on eqs. (9) through (14) are needed.
Check if moment capacity of the beam is greater than the overstrength moment capacity of the column.
Neglect the effect of the compression steel (conservative).
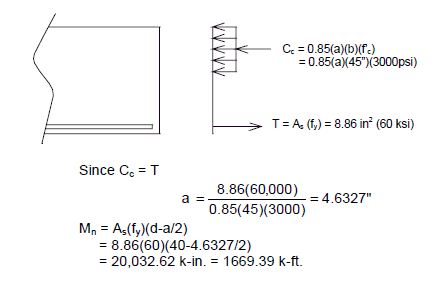
Compare moment capacity of beam versus overstrength moment capacity of the column:
- 1669.39 k-ft. > 1562.60 k-ft.
Moment capacity of beam is greater than the overstrength moment capacity of the column. O.K.
Design of reinforcement for the beam-column joint
- - Vertical reinforcement should be placed throughout a distance of hb/2 from the column face on each side of the column.
- From eq.(9):
- Asc = 15.70 in2
- From eq.(9):
- = 1.1f = 66 ksi.
- fyv = 60 ksi.
- Ajv = 0.125 (15.70) 66 / 60 = 2.16 in2
- - Reinforcement within the joint confines:
- From eq. (10):
- = 0.0625 (15.70) 66 / 60 = 1.08 in2
- From eq. (10):
- - Additional bottom of beam longitudinal reinforcement:
- From eq. (11):
- = 0.0625 (15.70) 66 / 60 = 1.08 in2
- From eq. (11):
- This reinforcement must be developed at a distance hb/2 away from the face of the column.
- - Hoop Reinforcement:
- From eq. (13):
- La = 40 in.
- fyh = 60 ksi
- ∴use ρs
- use #4 hoop reinforcement
- As = 0.1963 in2
- D’ = 36 – 2(2) – 4/8 = 31.5 in.
- ρs = 0.003238
- From eq. (15): = 7.70” spacing > 3” max. from Fig. 751.40.8.11.5.4. Therefore, Use S = 3”
Principal Tension and Compression Stresses in Column-Footing Joints
Column – Footing joints are essentially the same as inverted beam-column T joints. Eqs. (1) through (8) are applicable to column-footing joints except the beam height, hb, shall be changed to the footing height, hf.
Design of Reinforcement for Column-Footing Joint
The design of the reinforcement for column-footing joints is similar to that for beam-column T joint. From a joint performance viewpoint, it is desirable to bend the column bars inward toward the joint by using 90° hook bars, but this will cause undue congestion. Bending column bars away from the joint will increase the diagonal tension stress within the joint region. However, it makes a stable platform for supporting the column cage and prevents congestion. When the column reinforcement is bent outward, eqs. (9) through (14) shall be applied. Since the column inelastic action may develop in directions other than parallel to one of the principal axes of the footing, the amount of vertical reinforcement in eq. (9) shall be placed in each of the four quadrant areas outside the joint. In other words, a total vertical stirrup area of:
- (16)
shall be placed around the column.
Extra top reinforcement in the footing is also required in accordance with eq. (11). This reinforcement should pass through the column reinforcement or be placed as close as possible to the sides of the column and extend a distance of not less than l = 0.5*D + Ld, where Ld is the bar development length, beyond the face on both sides of the column.
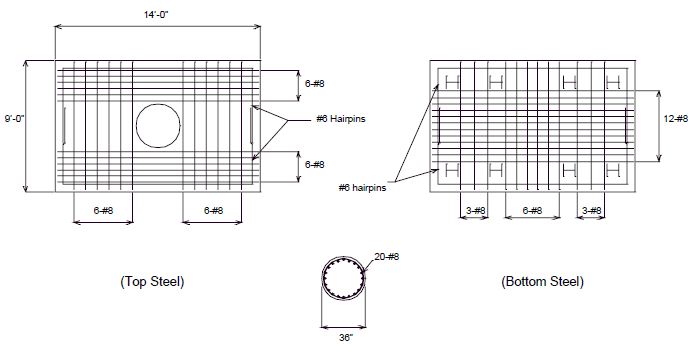
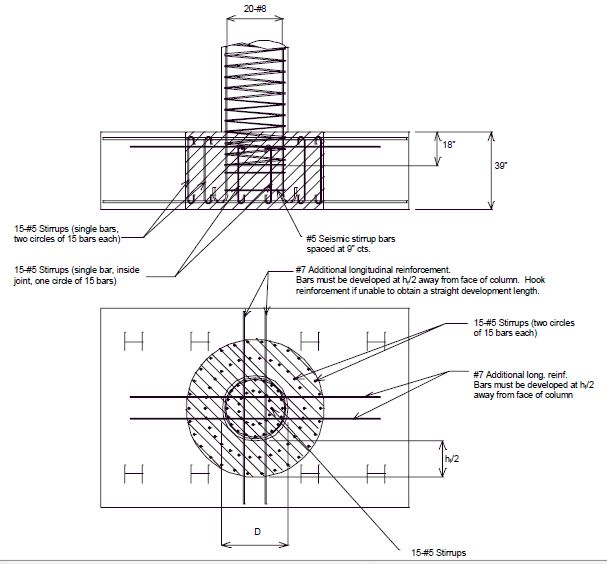
Example 751.40.8.11.5.2: A column is subjected to an axial load (due to dead and seismic loads) of 520 kips. The column diameter is 36 in. with 20 #8 bars for longitudinal reinforcement. All column reinforcement is bent outward into the footing away from the joint. The footing depth is 39 inches. The top and bottom reinforcement for the footing is shown in Fig. 751.40.8.11.5.10, below. Design the reinforcement details for the column-footing joint.
Solution:
The axial load for the column = 520 kips.
From Fig. 751.40.8.11.5.8 in Example 751.40.8.11.5.1, M0 = 1562.6 k-ft.
From eq.(1): = 480.8 kips
From eq. (3):
From eq. (2): =262.39 psi.
Vertical Axial Stress:
From eq. (6):
- = 136.21psi.
Horizontal Axial Stress:
- fh = 0 psi.
Principal Stresses:
From eq. (7):
- = 339.19 psi. ≤ 0.3(3000psi.) = 900 psi. O.K.
From eq. (8):
- = -202.98 psi. > 3.5 = 191.7 psi. Not O.K.
Since pt is greater than allowed, special joint reinforcement based on eqs. (9)through (14) are needed.
Check moment capacity
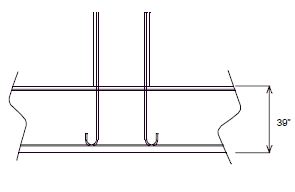
Check the moment capacity of footing in the long direction to see if it is greater than the overstrength moment capacity of the column.
Neglect the effect of the compression reinforcement.
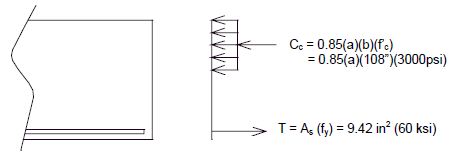
- Since Cc = T
- = 2.0523"
- Mn = As(fy)(d - a/2)
- = 9.42(60)(35-(2.0523/2))
- = 1600.17 k-ft.
Compare moment capacity of footing overstrength moment capacity of the column:
- 1600.17 k-ft > 1562.60 k-ft.
Moment capacity of the footing is greater than the overstrength moment of capacity of the column. O.K.
Check the moment capacity of the footing in the short direction to see if it is greater than the overstrength moment capacity of the column.
Neglect the effect of the compression reinforcement.
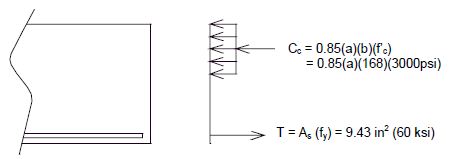
- Since Cc = T
- = 1.3207"
- Mn = As(fy)(d - a/2)
- = 9.43(60)(35-(1.3207/2))
- = 1619.11 k-ft.
Compare moment capacity of footing overstrength moment capacity of the column:
- 1619.11 k-ft > 1562.60 k-ft.
Moment capacity of the footing is greater than the overstrength moment of capacity of the column. O.K.
Design of reinforcement for the column-footing joint
- - Vertical reinforcement should be placed throughout a distance of hf/2 from the column face on each side of the column.
- From eq. (16):
- Asc = 15.71 in2
- = 1.1 fy = 66 ksi.
- fyv = 60 ksi.
- Ajv = 0.5 (15.71) (66 / 60) = 8.641 in2
- From eq. (16):
- - Reinforcement within the joint confines:
- From eqs. (9),(10) & (16):
-
- = 0.25 (15.71)(66/60) = 4.320 in2
-
- From eqs. (9),(10) & (16):
- - Additional top of footing longitudinal reinforcement:
-
- = 0.0625 (15.70)(66 / 60) = 1.08 in2
-
- This reinforcement must be developed at a distance hb/2 away from the face of the column and must be placed so that the reinforcement goes through the column reinforcement. Asb is required in both directions in the footing.
- - Hoop Reinforcement:
- From eq. (13):
- La = 35 in.
- fyh = 60 ksi
- = 0.004232
- = 0.003195
- ρs > ρs, min ∴use ρs
- Use #5 hoop reinforcement
- As = 0.3068
- D’ = 36 - 2(2) - 5/8” = 31.375”
- ρs = 0.004232
- From eq. (15): = 9.24"
- Use 9” Spacing
- Note: By adding 3 in. to footing depth in this example problem, the principal tensile stress in the joint would have been less than the maximum allowed tensile stress, thus eliminating the need for the special joint reinforcement other than the minimum required reinforcement. However, the practice of increasing footing depth to eliminate the need for the special joint reinforcement should be limited to increasing the footing depth a maximum of 6 inches.
751.40.8.12 Concrete Pile Cap Intermediate Bents
751.40.8.12.1 Design
751.40.8.12.1.1 Unit Stresses
| (1) | Reinforced Concrete | ||
| Class B Concrete (Substructure) | = 1,200 psi | = 3,000 psi | |
| Reinforcing Steel (Grade 60 | = 24,000 psi | = 60,000 psi | |
| = 10 | |||
| (2) | Structural Steel | ||
| Structural Carbon Steel (ASTM A709 Grade 36) | = 20,000 psi | = 36,000 psi | |
| (3) | Piling | ||
| (4) | Overstress | ||
| The allowable overstresses as specified in AASHTO Article 3.22 shall be used where applicable for service loads. | |||
751.40.8.12.1.2 Loads
| (1) | Dead Loads |
| (2) | Live Load |
| As specified on Bridge Memorandum. | |
| Impact of 30% is to be used for design of the beam. No impact is to be used for design of any other portion of bent including the piles. | |
| (3) | Temperature, Wind and Frictional Loads |
751.40.8.12.1.3 Distribution of Loads
| (1) | Dead Loads |
| Loads from stringers, girders, etc. shall be concentrated loads applied at the intersection of centerline of stringer and centerline of bearing. Loads from concrete slab spans shall be applied as uniformly, distributed loads along the centerline of bearing. | |
| (2) | Live Load |
| Loads from stringers, girders, etc. shall be applied as concentrated loads at the intersection of centerline of stringer and centerline of bearing. For concrete slab spans distribute two wheel lines over 10'-0" (normal to centerline of roadway) of substructure beam. This distribution shall be positioned on the beam on the same basis as used for wheel lines in Traffic Lanes for Substructure Design. | |
| (3) | Temperature, Wind and Frictional Loads |
751.40.8.12.1.4 Design Assumptions
LOADINGS
| (1) | Beam | |
| The beam shall be assumed continuous over supports at centerline of piles. | ||
| Intermediate bent beam caps shall be designed so that service dead load moments do not exceed the cracking moment of the beam cap (AASHTO Article 8.13.3, Eq. 8-2). | ||
| (2) | Piles | |
| (a) | Bending | |
| Stresses in the piles due to bending need not be considered in design calculations for Seismic Performance Category A. | ||
| (b) | Dead Loads, etc. | |
| Dead load of superstructure and substructure will be distributed equally to all piles which are under the main portion of the bent. | ||
751.40.8.12.2 Reinforcement
751.40.8.12.2.1 General
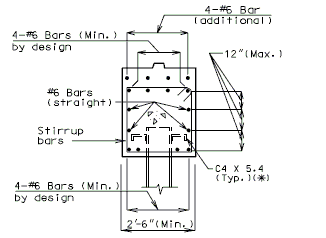
PRESTRESS DOUBLE-TEE STRUCTURES
|
|
| SECTION A-A | SECTION B-B |
| (*) | Channel shear connectors are to be used in Seismic Performance Categories B, C & D. For details not shown, see EPG 751.9 Bridge Seismic Design. |
| (**) | 2'-6" Min. for Seismic Performance Category A. 2'-9" Min. for Seismic Performance Categories, B, C & D. |
| Note: Use square ends on Prestress Double-Tee Structures. | |
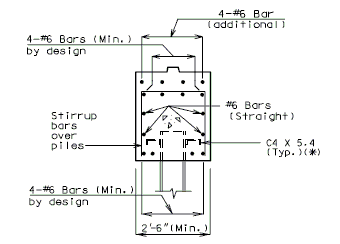
 |
|
| SECTION A-A | SECTION B-B |
| (*) | Channel shear connectors are to be used in Seismic Performance Categories B, C & D. |
| (**) | 2'-6" Min. for Seismic Performance Category A. 2'-9" Min. for Seismic Performance Categories, B, C & D. |
| Note: Use square ends on Prestress Double-Tee Structures. | |
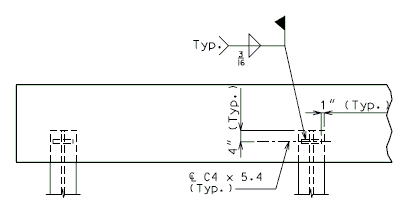
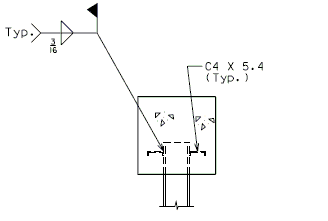
751.40.8.12.2.2 Anchorage of Piles for Seismic Performance Categories B, C & D
STEEL PILE
|
|
| PART ELEVATION | SECTION THRU BEAM |

| |
| PART PLAN |
CAST-IN-PLACE PILE
|
|
| PART ELEVATION | SECTION THRU BEAM |

| |
| PART PLAN |
751.40.8.12.2.3 Beam Reinforcement Special Cases
SPECIAL CASE I
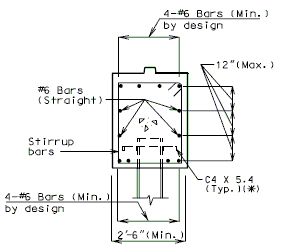
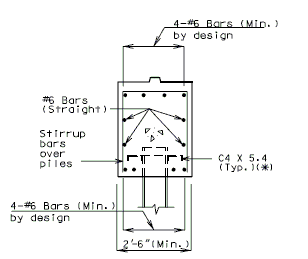
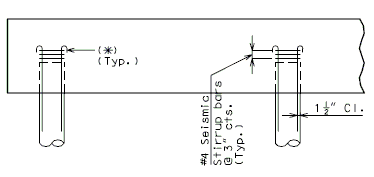
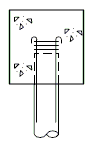
If centerline bearing is 12" or less on either side of centerline piles, for all piles (as shown above), use 4-#6 top and bottom and #4 at 12" cts. (stirrups), regardless of pile size.
SPECIAL CASE II
When beam reinforcement is to be designed assuming piles to take equal force, design for negative moment in the beam over the interior piles.
(*) Dimensions shown are for illustration purposes only.
751.40.8.12.3 Details
751.40.8.12.3.1 Sway Bracing
Refer to EPG 751.32.3.2.1 Sway Bracing.
751.40.8.12.3.2 Miscellaneous Details for Prestressed Girder
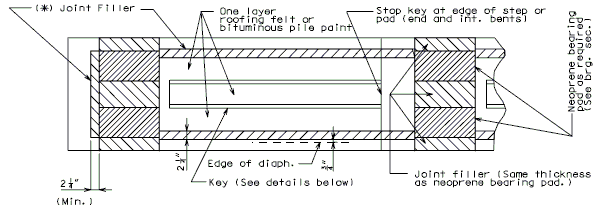
PRESTRESSED GIRDERS (INTEGRAL INT. BENT)
(Continuous Spans - No Longitudinal Beam Steps)
| (*) | ¼ Joint Filler for a P/S Double Tee Structure |
| ½ Joint Filler for a P/S I-Girder Structure |
PRESTRESSED GIRDERS (NON-INTEGRAL INT. BENT)
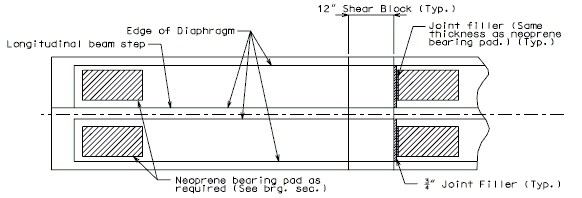
Longitudinal Beam Step and Shear Blocks shown)
DETAILS OF CONST. JOINT KEY
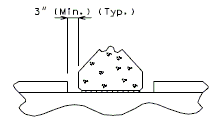
|
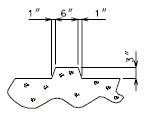
|
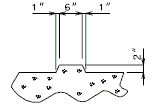
|
| PART ELEVATION | PART SECTION THRU KEYS (P/S I-GIRDERS) |
PART SECTION THRU KEYS (P/S DOUBLE TEE GIRDERS) |
751.40.8.13 Concrete Pile Cap Non-Integral End Bents
751.40.8.13.1 Design
751.40.8.13.1.1 Unit Stresses
| (1) | Reinforced Concrete | ||
| Class B Concrete (Substructure) | = 1,200 psi | = 3,000 psi | |
| Reinforcing Steel (Grade 60) | = 24,000 psi | = 60,000 psi | |
| = 10 | |||
| AASHTO Article 8.7.1) (*) | |||
| (2) | Structural Steel | ||
| Structural Carbon Steel (ASTM A709 Grade 36) | = 20,000 psi | = 36,000 psi | |
| (3) | Piling | ||
| (4) | Overstress | ||
| The allowable overstresses as specified in AASHTO Article 3.22 shall be used where applicable for Service Loads design method. | |||
| (*) | = 145 pcf., for = 150 pcf. | ||
751.40.8.13.1.2 Loads
| (1) | Dead Loads |
| (2) | Live Load |
| As specified on the Bridge Memorandum | |
| Impact of 30% is to be used for design of the beam. No impact is to be used for design of any other portion of bent including the piles. | |
| (3) | Temperature, Wind and Frictional Loads |
| Wind and temperature forces can be calculated based on longitudinal force distribution. |
751.40.8.13.1.3 Distribution of Loads
| (1) | Dead Loads |
| Loads from stringers, girders, etc. shall be concentrated loads applied at the intersection of centerline of stringer and centerline of bearing. | |
| (2) | Live Load |
| Loads from stringers, girders, etc. shall be applied as concentrated loads at the intersection of centerline of stringer and centerline of earing. | |
| (3) | Temperature |
| The force due to expansion or contraction applied at bearing pads are not used for stability or pile bearing computations. However, the movement due to temperature should be considered in the bearing pad design and expansion device design. | |
| (4) | Wing with Detached Wing Wall |
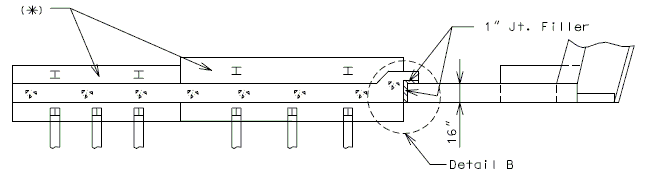
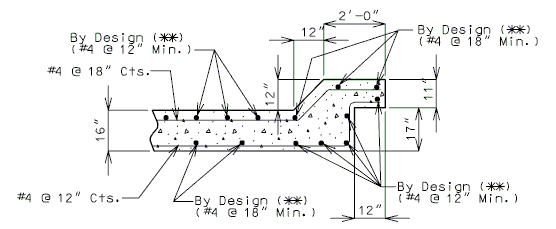
| (*) | Detached wing wall shown is for illustration purpose only. Design detached wing wall as a retaining wall. |
| (**) | See retaining wall design. |
751.40.8.13.1.4 Design Assumptions - Loadings
| 1) | Piles | ||||||||||||||||||||||
| a. | Stresses in the piles due to bending need not be considered in design calculations except for seismic design in categories B, C and D. | ||||||||||||||||||||||
| b. | The following four loading cases should be considered. | ||||||||||||||||||||||
| |||||||||||||||||||||||
| Where, | |||||||||||||||||||||||
| LL | = live load | ||||||||||||||||||||||
| DL | = dead load of superstructure, substructure and one half of the apporach slab | ||||||||||||||||||||||
| SUR | = two feet of live load surcharge | ||||||||||||||||||||||
| E | = dead load of earth fill | ||||||||||||||||||||||
| EP | = equivalent fluid pressure of earth | ||||||||||||||||||||||
| Maximum pile pressure = pile capacity | |||||||||||||||||||||||
| Minimum pile pressure = 0 (tension on a pile will not be allowed for any combination of forces exept as noted) | |||||||||||||||||||||||
| 2) | Analysis Procedure | ||||||||||||||||||||||
| a. | Find the lateral stiffness of a pile, : | ||||||||||||||||||||||
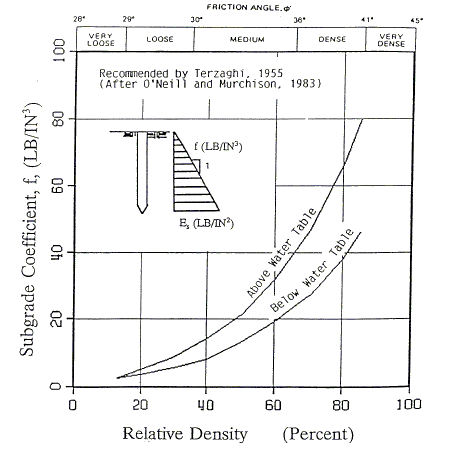
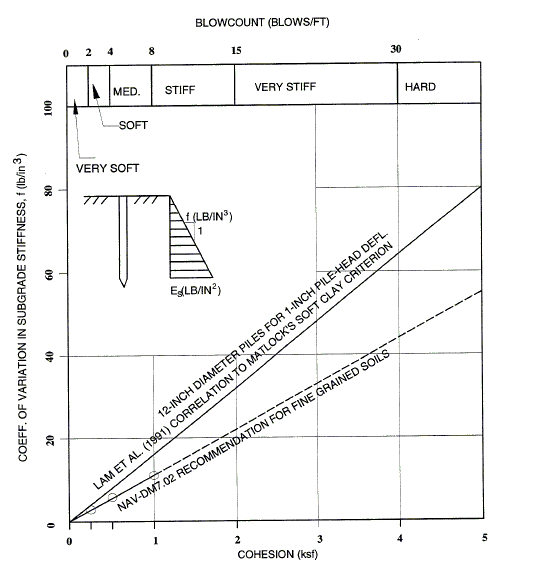
| With fixed pile-head (i.e., only translation movement is allowed but no rotation allowed): The lateral stiffness of a pile can be estimated using Figures 1 and 3 or 2 and 3 for pile in cohesionless or cohesive soil, respectively. The method of using Figures 1, 2, and 3 to find lateral stiffness is called Linear Subgrade Modulus Method. Usually the significant soil-pile interaction zone for pile subjected to lateral movement is confined to a depth at the upper 5 to 10 pile diameters. Therefore, simplified single layer stiffness chart shown in Figure 3 is appropriate for lateral loading. The coefficient in Figures 1 and 2 is used to define the subgrade modulus at depth “z” representing the soil stiffness per unit pile length. For the purpose of selecting an appropriate value, the soil condition at the upper 5 pile diameters should be used. Since soil property, friction angle , or cohesion c, is needed when Figure 1 or 2 is used, determine soil properties based on available soil boring data. If soil boring data is not available, one can conservatively use value of 0.1 in Figure 3. Designer may also use soil properties to convert SPT N value to friction angle , or cohesion c, for granular or cohesive soil, respectively. Figures 1 and 2 were based on test data for smaller-diameter (12 inches) piles, but can be used for piles up to about 24 inches in diameter. In Figure 2, the solid line (by Lam et al. 1991) shall be used in design. | |||||||||||||||||||||||
| b. | Find the axial stiffness of a pile, : | ||||||||||||||||||||||
| For friction pile, may be determined based on a secant stiffness approach as described in EPG 751.9 Bridge Seismic Design or by the in-house computer program “SPREAD” where is calculated as: | |||||||||||||||||||||||
| Equation (1) | |||||||||||||||||||||||
| Where: | |||||||||||||||||||||||
| = cross sectional area of pile | |||||||||||||||||||||||
| = elastic modulus of pile | |||||||||||||||||||||||
| = total length of pile | |||||||||||||||||||||||
| = secant stiffness due to ultimate friction capacity of the pile as described in EPG 751.9.2.6.3 Pile Axial Stiffness | |||||||||||||||||||||||
| = secant stiffness due to ultimate bearing capacity of the pile as described in EPG 751.9.2.6.3 Pile Axial Stiffness | |||||||||||||||||||||||
| For HP bearing pile on rock shall be calculated as: | |||||||||||||||||||||||
| Equation (2) | |||||||||||||||||||||||
| Or Conservatively, may be determined as: | |||||||||||||||||||||||
| Equation (3) | |||||||||||||||||||||||
| |||||||||||||||||||||||
| Recommended Coefficient of Variation in Subgrade Modulus with Depth for Sand | |||||||||||||||||||||||
| |||||||||||||||||||||||
| Recommended Coefficient of Variation in Subgrade Modulus with Depth for Clay | |||||||||||||||||||||||
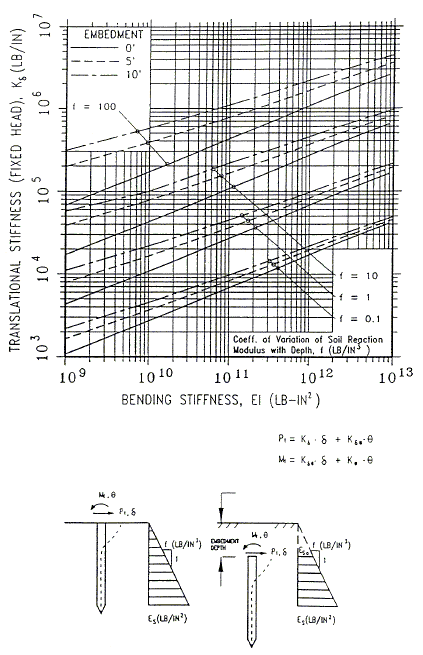
| |||||||||||||||||||||||
| |||||||||||||||||||||||
| Lateral Embedded Pile-Head Stiffness | |||||||||||||||||||||||
| c. | Find the equivalent cantilever pile length, | ||||||||||||||||||||||
| For the structural model used in the structural analyses of loading cases I through IV. As shown in figure below, length L can be calculated as: | |||||||||||||||||||||||
| Equation (4) | |||||||||||||||||||||||
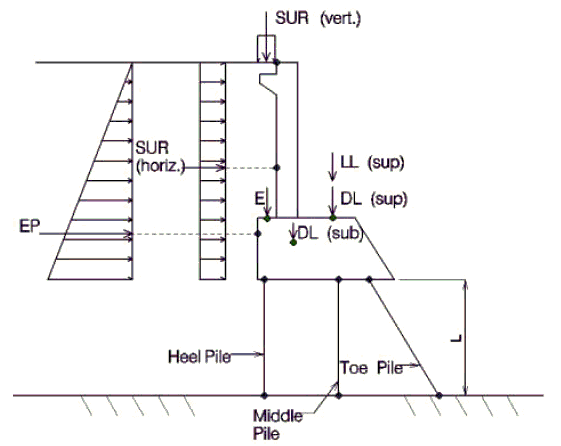
| |||||||||||||||||||||||
| Structural Model | |||||||||||||||||||||||
| d. | Find the equivalent pile area, : | ||||||||||||||||||||||
| Once the equivalent cantilever pile length has been determined from step (c) above, the equivalent axial rigidity of the pile, , can be calculated as . Then, the equivalent pile area, , is equal to | |||||||||||||||||||||||
| Equation (5) | |||||||||||||||||||||||
| e. | Perform structural analyses for loading cases I through IV. | ||||||||||||||||||||||
| Use computer programs STRUCT3D, SAP2000 or any other program capable of running static analysis. | |||||||||||||||||||||||
| f. | Check abutment movement at the top of backwall and at the bottom of beam cap | ||||||||||||||||||||||
| Maximum movement away from the backfill shall not be greater than 1/8". Maximum movement toward the backfill shall not be greater than 1/4". | |||||||||||||||||||||||
| g. | Check pile axial loads from the analysis with the allowable pile axial load capacity. | ||||||||||||||||||||||
| h. | Check overturning of bent | ||||||||||||||||||||||
| Conservatively, use the same equivalent cantilever pile length, . Check overturning of bent at the bottom of toe pile for loading cases I and II(Figure of Structural model). | |||||||||||||||||||||||
| |||||||||||||||||||||||
| 5) | Deadman Anchorage System | ||||||||||||||||||||||
| Deadman anchorage can be used when the abutment movement exceeds the allowable movement. | |||||||||||||||||||||||
| The size and location of deadman anchorage shall be designed appropriately to maintain the stability of the abutment. | |||||||||||||||||||||||
| The deadman forces may be used to resist overturning with the approval of the Structural Project Manager. | |||||||||||||||||||||||
| 6) | Passive Pressure Shear Key (if applicable) | ||||||||||||||||||||||
| Passive pressure shear key may be used when the abutment movement exceeds the allowable movement. | |||||||||||||||||||||||
| The passive resistance of soil to the lateral force at shear keys may be used with the approval of structural project manager. | |||||||||||||||||||||||
751.40.8.13.1.5 Deadman Anchors
Design Assumptions
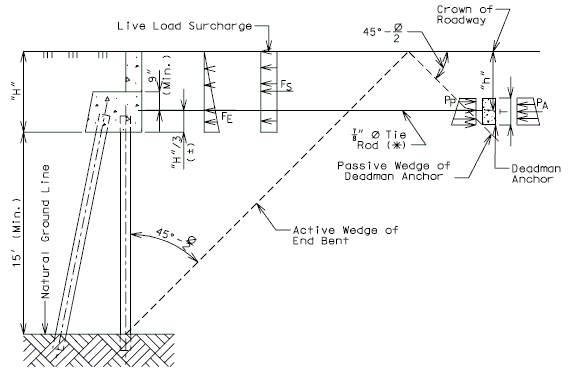
| Length of Deadman = | |
| Number of tie rods required = | |
| = Active earth pressure on deadman, in lb./ft. = (120 pcf) | |
| (**) | = Passive earth pressure on deadman, in lb./ft. = (120 pcf) |
| = Earth pressure on end bent, in lb. = 0.5(120 pcf) (length of beam) | |
| = Surcharge on end bent, in lb. = | |
| (***) | = 8.0 kips for 7/8" Ø tie rod and 10.50 kips for 1" Ø tie rods (Capacity of the tie rods based on a maximum skew of 30°.) |
| * | If the number of 7/8" Ø tie rods causes too long of a deadman, then try 1" Ø tie rods. |
| ** | For seismic loads only, use = 4 kips/sq.ft. as the ultimate capacity of compacted fill. |
| *** | For seismic loads only, the allowable stress in the tie rod may be taken as the yield stress of the rod. |
Notes:
No more than 20% of deadman may fall outside of the roadway shoulders. To prevent more than 20% limit, using a deeper deadman to reduce its length. If this is not possible, the total passive pressure resistance should be calculated by summing the resistance from the different fill depths.
When deadman anchors are to be used, design the piles for a factor of safety of 1.0 for sliding and design deadman anchors to resist all horizontal earth forces with a factor of safety of 1.0. This will result in a factor of safety for sliding of 2.0. For special cases, see the Structural Project Manager.
Design Example
| Assume: | |
| Roadway width = 36', Out-Out slab width = 36' + 2 x 16" = 38.67' | |
| Skew = , Length of Beam = | |
| Beam depth = , , | |
| , use | |
| Assume (Deadman anchor depth) | |
| Determine Earth and Surcharge Forces | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| Determine number of Tie Rods required | |
| Try 7/8"Ø Rods: kips | |
| Number of Rods required = | |
| Use 12-7/8"Ø Rie Rods. | |
| Determine length of Deadman | |
| Length of Deadman required = | |
| Tie Rod spacing = minimum, ok. | |
| Length of Deadman provided = | |
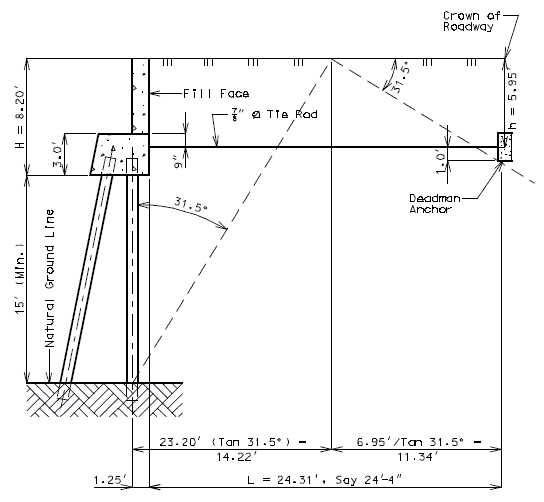
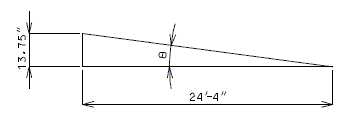
| 1) | Check tie rod skew angle at Fill Face of End Bent | |
| , tie capacity ok. | ||
| ||
| 2) | Check criteria for Deadman Anchors extending into Fill Slope | |
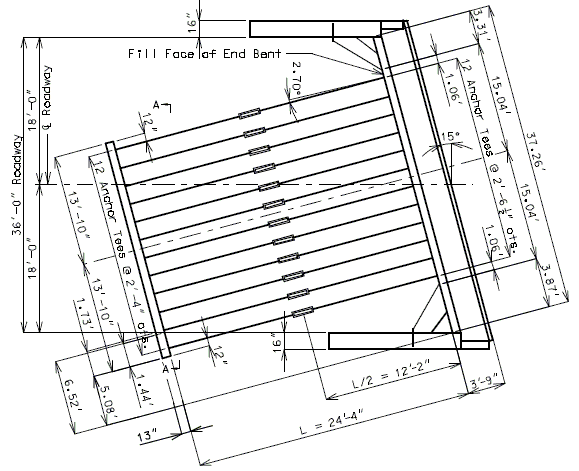
| ||
A) Extension of Deadman into Fill Slope Length of Deadman extending into Fill Slope = 0.2 (Length of Deadman) = Length of Deadman extending into Fill Slope (Length of Deadman), ok Note: See below for Section A-A details. B) Cover of Deadman in Fill Slope
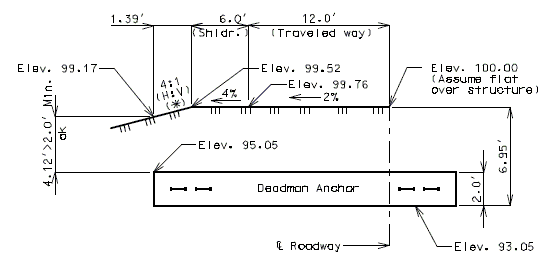
DETAIL AT FILL SLOPE
Note:
(*) Fill slope shown is for illustration purpose only, see roadway plans.
751.40.8.13.2 Reinforcement
751.40.8.13.2.1 Wide Flange Beams, Plate Girders and Prestressed Girders
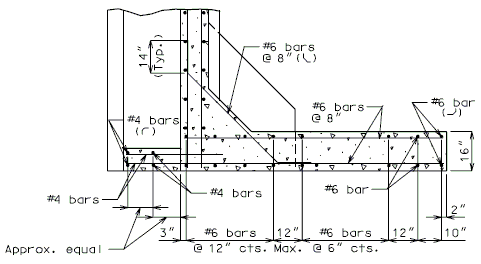
END BENT WITH EXPANSION DEVICE
|
|
| SECTION A-A | |
| PART ELEVATION |
Notes:
(1) See details for reinforcement of end bent backwall.
(2) #6-H bars and #4-H bars in backwall of skewed bridges shall be bent in field if required.
(3) Center #5 bars in backwall.
Epoxy coat all reinforcing in end bents with expansion devices. See ______ for details of protective coating and sloping top of beam to drain.
|
|
| DETAIL OF #5 BARS SHAPE 19 | |
| PART PLAN B-B |
END BENT WITHOUT EXPANSION DEVICE
|
|
| SECTION A-A | |
| PART ELEVATION |
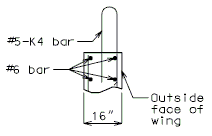
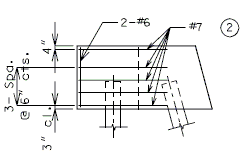
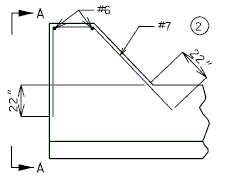
END BENT WING
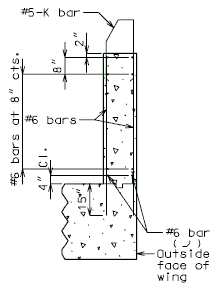 | |
|
|
| SECTION A-A | |
| TYPICAL ELEVATION OF WING |
Note: (1) Development length
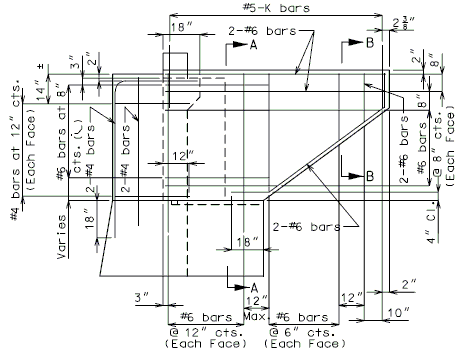
|
| ||||||||||||
| SECTION B-B | |||||||||||||
|
| ||||||||||||
| PART SECTION THRU BENTS WITH PASSIVE PRESSURE | |||||||||||||
| HORIZONTAL SECTION THRU WING (K bars not shown for clarity) |
END BENT BEAM HEEL
|
|
| ELEVATION A-A (TYP.) | PART PLAN OF BEAM (SQUARE) |
|
|
| PART PLAN OF BEAM - SKEWS THRU 15° - LEFT ADVANCE SHOWN | |
|
|
|
| SECTION B-B | ||
| PART PLAN OF BEAM - SKEWS OVER 15° - LEFT ADVANCE SHOWN | ||
Note:
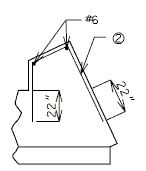
Vertical spacing for #7 bars shown in Elevation A-A is typical for all types of end bent beams.
For a long distance between heel pile and bearing beam investigate for use of larger bars; e.g. larger skews where the shear line does not fall within the bearing beam.
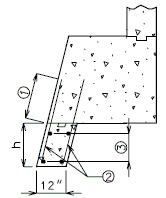
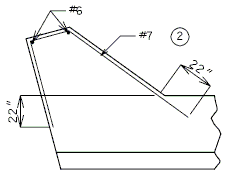
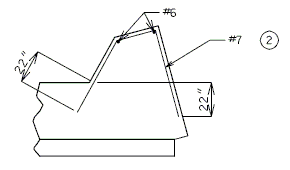
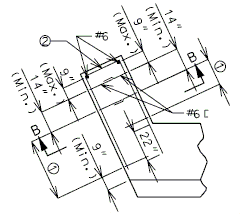
| Pile Load Not Greater | (1) Hair-Pin Stirrups | (2) Horizontal Rebar around Heel Pile | |||
| Skew thru 30° | Skew 31° thru 45° | Skew 46° thru 60° | Skew over 60° | ||
| 140 kips | #6 @ 9" | 5-#7 | 5-#7 | 5-#8 | By Design |
| 194 kips | #6 @ 6" | 5-#7 | 5-#8 | By Design | By Design |
Use 21" horizontal leg.
END BENT BACKWALL
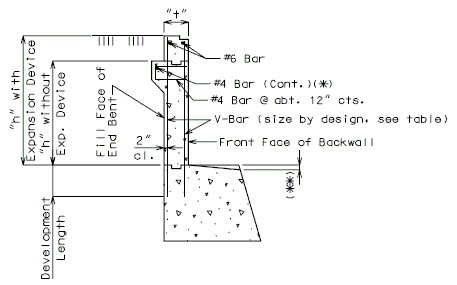
| V-BAR SIZE AND SPACING | |||
| h (feet) |
t (inch) |
Fill Face Reinforcement |
Front Face Reinforcement |
| 1-6 | 12 | #5 @ 12" | #5 @ 12" |
| 7 | 12 | #5 @ 12" | #5 @ 12" |
| 8 | 12 | #5 @ 12" | #5 @ 12" |
| 9 | 12 | #6 @ 12" | #5 @ 12" |
| 10 | 12 | #6 @ 10" | #5 @ 12" |
| 11 | 15 | #6 @ 10" | #5 @ 12" |
| 12 | 15 | #6 @ 8" | #5 @ 12" |
| 13 | 18 | #6 @ 8" | #5 @ 12" |
| 14 | 18 | #6 @ 6" | #5 @ 12" |
Note:
All reinforcement is grade 60.
Design is based on 45 lbs. per cu. ft. equivalent fluid pressure and 90 lbs. per sq. ft. live load surcharge.
Epoxy coat all reinforcing steel in beam and backwall on non-integral end bents with expansion devices.
751.40.8.14 Concrete Pile Cap Integral End Bents
751.40.8.14.1 Design
751.40.8.14.1.1 Design Unit Stresses
- Reinforced Concrete
- Class B Concrete (Substructure) = 1,200 psi, = 3,000 psi
- Reinforcing Steel (Grade 60) = 24,000 psi = 60,000 psi
- = 10
- = (AASHTO Article 8.7.1)(*)
- Structural Steel
- Structural Carbon Steel (ASTM A709 Grade 36) = 20,000 psi = 36,000 psi
- Piling
- See the Bridge Memorandum if pile capacity is indicated.
- Overstress
- The allowable overstresses as specified in AASHTO Article 3.22 shall be used where applicable for Service Loads design method.
(*)
751.40.8.14.1.2 Loads
- Dead Loads
- Live Load
- As specified on the Bridge Memorandum.
- Impact of 30% is to be used for design of the beam. No impact is to be used for design of any other portion of bent including the piles.
- Temperature, Wind and Frictional Loads
751.40.8.14.1.3 Distribution of Loads
- Dead Loads
- Loads from stringers, girders, etc. shall be concentrated loads applied at the intersection of centerline of stringer and centerline of bearing. Loads from concrete slab spans shall be applied as uniformly, distributed loads along the centerline of bearing.
- Live Load
- Loads from stringers, girders, etc. shall be applied as concentrated loads at the intersection of centerline of stringer and centerline of bearing. For concrete slab spans distribute two wheel lines over 10'-0" (normal to centerline of roadway) of substructure beam. This distribution shall be positioned on the beam on the same basis as used for wheel lines in Traffic Lanes for Substructure Design.
- Wing with Detached Wing Wall
- When wing length, L, is greater than 17 feet, use maximum length of 10 feet rectangular wing wall combined with a detached wing wall. When detached wing walls are used, no portion of the bridge live load shall be assumed distributed to the detached wing walls. Design detached wing wall as a retaining wall. (The weight of barrier or railing on top of the wall shall be included in Dead Load.)
751.40.8.14.1.4 Design Examples
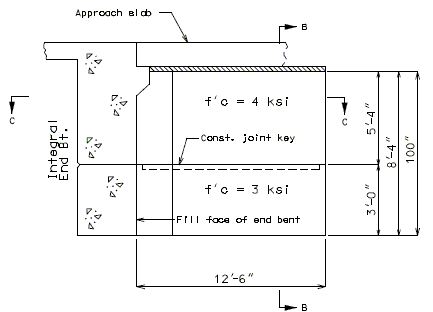
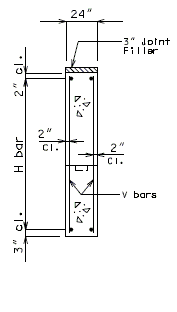
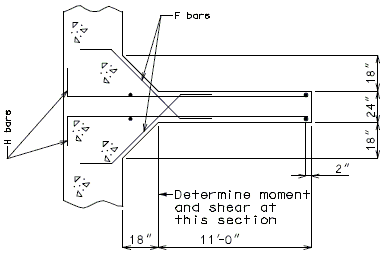
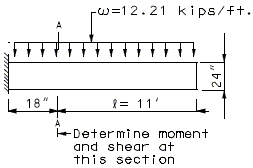
Design H-bar and F-bar of an intermediate wing as shown in the figures below (wing length = 12.5', wing thickness = 24", wing height = 8'-4"), a Seismic Force of = 12.21 kips/ft. is applied on the wall.
|
|
| Section Near Intermediate Wing | Section B-B |
|---|---|
|
|
| Interior Wing Design | |
| Section C-C | |
Solve: Assume #6 V bar, #8 H bar, #6 F bar
| 1.) | Design H-bar for bending |
| . | |
| At Section A-A: | |
| Use | |
| As (Req'd) = | |
| Try No. 8 @ 9", USE | |
| Say 11 spacings, 12 bars (Each Face) | |
| Total Area = USE 12-No. 8 H-bar (Each Face) |
| 2.) | Design F-bar for shear |
| (AASHTO Article 8.16.6.1.1) | |
| At Section A-A: | |
| No needed by AASHTO Article 8.16.6.3.1. | |
| Minimum shear reinforcement is required by AASHTO Article 8.19.1.1(a).(ACI 318-95 11.5.5.1) | |
| F-bar is a single group of parallel bars, all bent up at the same distance from support (no "spacing" along the "L" direction of the wing). | |
| Try No. 6 @ 12" F-bar (each face). | |
| Try say 8 spacing, 9 bars (each face). | |
| Since seismic force is a cyclic loading, assume one bar works at any instance. | |
| Check | |
| O.K. by AASHTO Article 8.16.6.3.4. | |
| USE 9 No. 6 F-bars (each face). |
751.40.8.14.2 Reinforcement
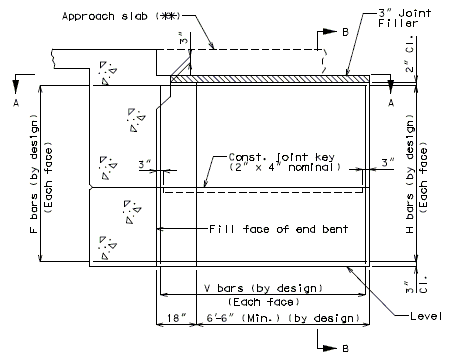
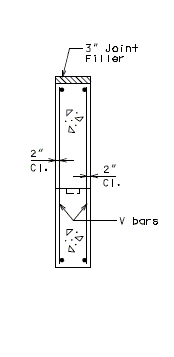
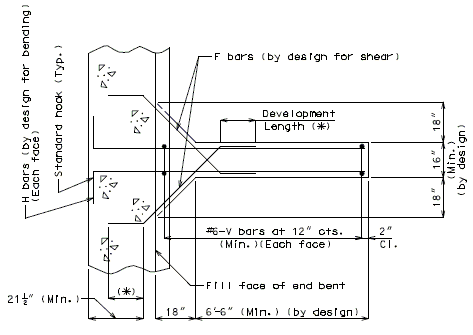
751.40.8.14.2.1 Earthquake Loads at End Bent – Intermediate Wing (Seismic Shear Wall)
|
|
| Section Near Intermediate Wing | Section B-B |
|---|---|
|
|
| Section A-A | |
| * | Use 1.25 x development length for seismic design. |
| ** | Additional reinforcing steel by design if required. |
| Note: | Make sure reinforcement does not interfere with girders. |
751.40.8.15 Cast-In-Place Concrete Retaining Walls
751.40.8.15.1 Loads
Dead Loads
Dead loads shall be determined from the unit weights in EPG 751.2.1.1 Dead Load.
Equivalent Fluid Pressure (Earth Pressures)
| Additional Information |
| AASHTO 3.20.1 |
For determining equivalent earth pressures for Group Loadings I through VI the Rankine Formula for Active Earth Pressure shall be used.
Rankine Formula: where:
- Ca = = coefficient of active earth pressure
- Pa = equivalent active earth pressure
- H = height of the soil face at the vertical plane of interest
- = unit weight of soil
- = slope of fill in degrees
- = angle of internal friction of soil in degrees
Example
Given:
- δ = 3:1 (H:V) slope
- ϕ = 25°
- γs = 0.120 kcf
- H = 10 ft
δ = arctan = 18.4°
Ca = = 0.515
Pa = (1/2)(0.515)(0.120 kips/ft3)(10 ft)2 = 3.090 kips per foot of wall length
The ϕ angle shall be determined by the Materials Division from soil tests. If the ϕ angle cannot be provided by the Construction and Materials Division a ϕ angle of 27 degrees shall be used.
Drainage shall be provided to relieve water pressure from behind all cast-in-place concrete retaining walls. If adequate drainage can not be provided then walls shall be designed to resist the maximum anticipated water pressure.
Surcharge Due to Point, Line and Strip Loads
Surcharge due to point and line loads on the soil being retained shall be included as dead load surcharge. The effect of these loads on the wall may be calculated using Figure 5.5.2B from AASHTO.
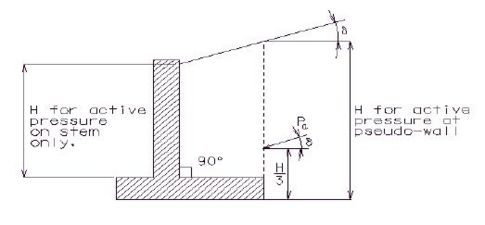
Surcharge due to strip loads on the soil being retained shall be included as a dead load surcharge load. The following procedure as described in Principles of Foundation Engineering by Braja M. Das (1995) shall be applied to calculate these loads when strip loads are applicable. An example of this application is when a retaining wall is used in front of an abutment so that the wall is retaining the soil from behind the abutment as a strip load on the soil being retained by the wall.
The portion of soil that is in the active wedge must be determined because the surcharge pressure only affects the wall if it acts on the active wedge. The actual failure surface in the backfill for the active state can be represented by ABC shown in the figure below. An approximation to the failure surface based on Rankine's active state is shown by dashed line AD. This approximation is slightly unconservative because it neglects friction at the pseudo-wall to soil interface.
The following variables are shown in the figure below:
- β = slope of the active failure plane in degrees
- δ = slope of fill in degrees
- H = height of the pseudo-wall (fom the bottom of the footing).
- L1 = distance from back of stem to back of footing heel
- L2 = distance from footing heel to intersection of failure plane with ground surface
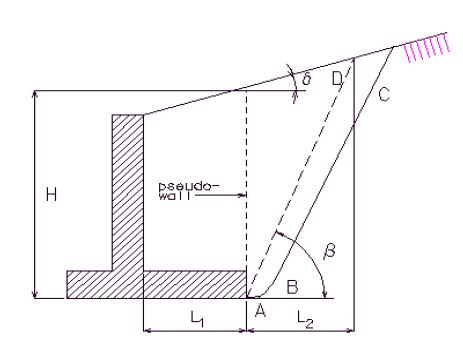
In order to determine β, the following equation which has been derived from Rankine's active earth pressure theory must be solved by iteration:
- ϕ = angle of internal friction of soil in degrees
A good estimate for the first iteration is to let β = 45° + (ϕ/2). In lieu of iterating the above equation a conservative estimate for β is 45°. Once β has been established, an estimate of L1 is needed to determine L2. From the geometry of the variables shown in the above figure:
The resultant pressure due to the strip load surcharge and its location are then determined. The following variables are shown in the figure below:
- q = load per unit area
- Ps = resultant pressure on wall due only to surcharge earth pressure
- = location of Ps measured from the bottom of the footing
- L3 = distance from back of stem to where surcharge pressure begins
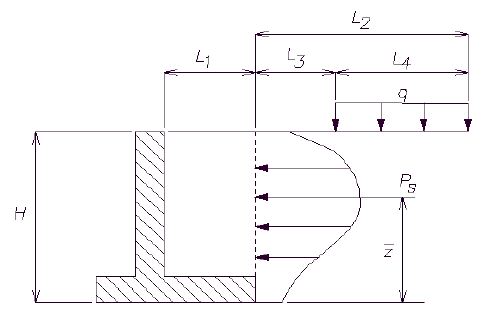
From the figure:
- Ps = where
- where
When applicable, Ps is applied to the wall in addition to other earth pressures. The wall is then designed as usual.
Live Load Surcharge
| Additional Information |
| AASHTO 3.20.3 & 5.5.2 |
Live load surcharge pressure of not less than two feet of earth shall be applied to the structure when highway traffic can come within a horizontal distance equal to one-half of the wall height, measured from the plane where earth pressure is applied.
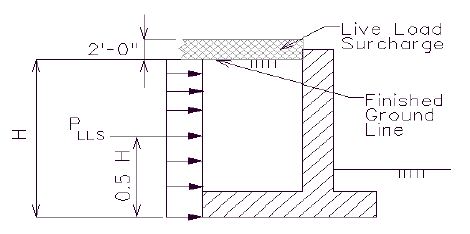
- PLLS = (2 ft.) γs Ca H = pressure due to live load surcharge only
- γs = unit weight of soil (Note: AASHTO 5.5.2 specifies a minimum of 125 pcf for live load surcharge, MoDOT policy allows 120 pcf as given from the unit weights in EPG 751.2.1.1 Dead Load.)
- Ca = coefficient of active earth pressure
- H = height of the soil face at the vertical plane of interest
The vertical live load surcharge pressure should only be considered when checking footing bearing pressures, when designing footing reinforcement, and when collision loads are present.
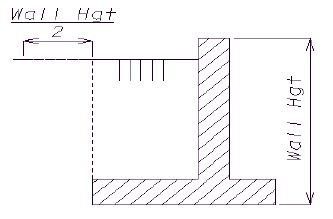
Live Load Wheel Lines
Live load wheel lines shall be applied to the footing when the footing is used as a riding or parking surface.
| Additional Information |
| AASHTO 3.24.5.1.1 & 5.5.6.1 |
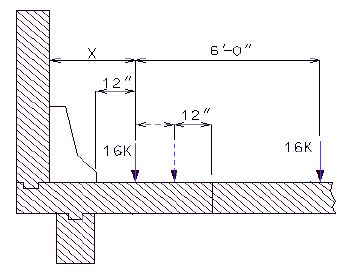
Distribute a LLWL equal to 16 kips as a strip load on the footing in the following manner.
- P = LLWL/E
- where E = 0.8X + 3.75
- X = distance in ft. from the load to the front face of the wall
| Additional Information |
| AASHTO 3.24.2 & 3.30 |
Two separate placements of wheel lines shall be considered, one foot from the barrier or wall and one foot from the toe of the footing.
Collision Forces
| Additional Information |
| AASHTO Figure 2.7.4B |
Collision forces shall be applied to a wall that can be hit by traffic. Apply a point load of 10 kips to the wall at a point 3 ft. above the finished ground line.
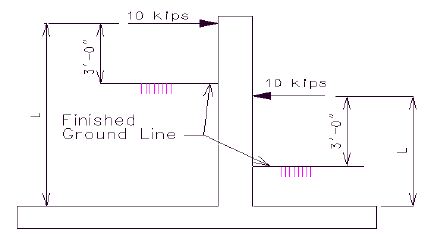
Distribute the force to the wall in the following manner:
- Force per ft of wall = (10 kips)/2L
When considering collision loads, a 25% overstress is allowed for bearing pressures and a factor of safety of 1.2 shall be used for sliding and overturning.
Wind and Temperature Forces
These forces shall be disregarded except for special cases, consult the Structural Project Manager.
When walls are longer than 84 ft., an expansion joint shall be provided.
Contraction joint spacing shall not exceed 28 feet.
Seismic Loads
Retaining walls in Seismic Performance Category A (SPC A) and SPC B that are located adjacent to roadways may be designed in accordance with AASHTO specifications for SPC A. Retaining walls in SPC B which are located under a bridge abutment or in a location where failure of the wall may affect the structural integrity of a bridge shall be designed to AASHTO specifications for SPC B. All retaining walls located in SPC C and SPC D shall be designed in accordance to AASHTO specifications for the corresponding SPC.
In seismic category B, C and D determine equivalent fluid pressure from Mononobe-Okabe static method.
| Additional Information |
| 1992 AASHTO Div. IA Eqns. C6-3 and C6-4 |
PAE = equivalent active earth pressure during an earthquake
PAE = 0.5 γsH2(1 - kv)KAE where
KAE = seismic active pressure coefficient
γs = unit weight of soil
| Additional Information |
| AASHTO 5.2.2.3 & Div. IA 6.4.3 |
kv = vertical acceleration coefficient
kh = horizontal acceleration coefficient which is equal to 0.5A for all walls,
- but 1.5A for walls with battered piles where
- A = seismic acceleration coefficient
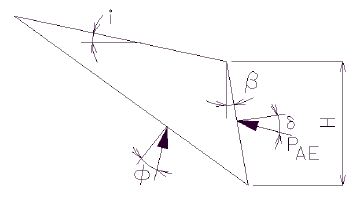
The following variables are shown in the figure below:
ϕ = angle of internal friction of soil
θ =
β = slope of soil face
δ = angle of friction between soil and wall in degrees
i = backfill slope angle in degrees
H = distance from the bottom of the part of the wall to which the pressure is applied to the top of the fill at the location where the earth pressure is to be found.
Group Loads
For SPC A and B (if wall does not support an abutment), apply AASHTO Group I Loads only. Bearing capacity, stability and sliding shall be calculated using working stress loads. Reinforced concrete design shall be calculated using load factor design loads.
| Additional Information |
| AASHTO Table 3.22.1A |
AASHTO Group I Load Factors for Load Factor Design of concrete: γ = 1.3
βD = 1.0 for concrete weight
βD = 1.0 for flexural member
βE = 1.3 for lateral earth pressure for retaining walls
βE = 1.0 for vertical earth pressure
βLL = 1.67 for live load wheel lines
βLL = 1.67 for collision forces
| Additional Information |
| AASHTO 5.14.2 |
βE = 1.67 for vertical earth pressure resulting from live load surcharge
βE = 1.3 for horizontal earth pressure resulting from live load surcharge
For SPC B (if wall supports an abutment), C, and D apply AASHTO Group I Loads and seismic loads in accordance with AASHTO Division IA - Seismic Design Specifications.
| Additional Information |
| AASHTO Div. IA 4.7.3 |
When seismic loads are considered, load factor for all loads = 1.0.
751.40.8.15.3 Unit Stresses
Concrete Concrete for retaining walls shall be Class B Concrete (f'c = 3000 psi) unless the footing is used as a riding surface in which case Class B-1 Concrete (f'c = 4000 psi) shall be used.
Reinforcing Steel
Reinforcing Steel shall be Grade 60 (fy = 60,000 psi).
Pile Footing
For steel piling material requirements, see the unit stresses in EPG 751.50 Standard Detailing Notes.
Spread Footing
For foundation material capacity, see Foundation Investigation Geotechnical Report.
751.40.8.15.4 Design
For epoxy coated reinforcement requirements, see EPG 751.5.9.2.2 Epoxy Coated Reinforcement Requirements.
If the height of the wall or fill is a variable dimension, then base the structural design of the wall, toe, and heel on the high quarter point between expansion joints.

| Additional Information |
| AASHTO 5.5.5 |
751.40.8.15.4.1 Spread Footings
Location of Resultant
The resultant of the footing pressure must be within the section of the footing specified in the following table.
| When Retaining Wall is Built on: | AASHTO Group Loads I-VI | For Seismic Loads |
|---|---|---|
| Soila | Middle 1/3 | Middle 1/2 b |
| Rockc | Middle 1/2 | Middle 2/3 |
| a Soil is defined as clay, clay and boulders, cemented gravel, soft shale, etc. with allowable bearing values less than 6 tons/sq. ft. | ||
| b MoDOT is more conservative than AASHTO in this requirement. | ||
| c Rock is defined as rock or hard shale with allowable bearing values of 6 tons/sq. ft. or more. | ||
Note: The location of the resultant is not critical when considering collision loads.
Factor of Safety Against Overturning
| Additional Information |
| AASHTO 5.5.5 |
AASHTO Group Loads I - VI:
- F.S. for overturning ≥ 2.0 for footings on soil.
- F.S. for overturning ≥ 1.5 for footings on rock.
For seismic loading, F.S. for overturning may be reduced to 75% of the value for AASHTO Group Loads I - VI. For seismic loading:
- F.S. for overturning ≥ (0.75)(2.0) = 1.5 for footings on soil.
- F.S. for overturning ≥ (0.75)(1.5) = 1.125 for footings on rock.
For collision forces:
- F.S. for overturning ≥ 1.2.
Factor of Safety Against Sliding
| Additional Information |
| AASHTO 5.5.5 |
Only spread footings on soil need be checked for sliding because spread footings on rock or shale are embedded into the rock.
- F.S. for sliding ≥ 1.5 for AASHTO Group Loads I - VI.
- F.S. for sliding ≥ (0.75)(1.5) = 1.125 for seismic loads.
- F.S. for sliding ≥ 1.2 for collision forces.
The resistance to sliding may be increased by:
- adding a shear key that projects into the soil below the footing.
- widening the footing to increase the weight and therefore increase the frictional resistance to sliding.
Passive Resistance of Soil to Lateral Load
The Rankine formula for passive pressure can be used to determine the passive resistance of soil to the lateral force on the wall. This passive pressure is developed at shear keys in retaining walls and at end abutments.
| Additional Information |
| AASHTO 5.5.5A |
The passive pressure against the front face of the wall and the footing of a retaining wall is loosely compacted and should be neglected when considering sliding.
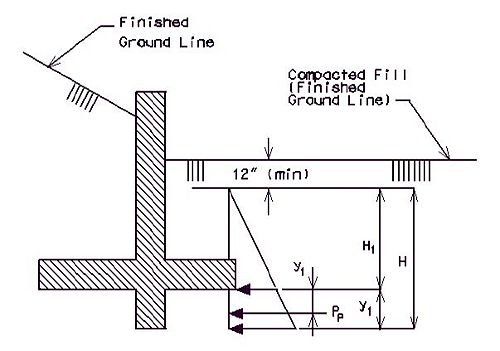
Rankine Formula: where thefollowing variables are defined in the figure below
- Cp =
- y1 =
- Pp = passive force at shear key in pounds per foot of wall length
- Cp = coefficient of passive earth pressure
- = unit weight of soil
- H = height of the front face fill less than 1 ft. min. for erosion
- H1 = H minus depth of shear key
- y1 = location of Pp from bottom of footing
- = angle of internal friction of soil
| Additional Information |
| AASHTO 5.5.2 |
The resistance due to passive pressure in front of the shear key shall be neglected unless the key extends below the depth of frost penetration.
| Additional Information |
| MoDOT Materials Division |
Frost line is set at 36 in. at the north border of Missouri and at 18 in. at the south border.
Passive Pressure During Seismic Loading
During an earthquake, the passive resistance of soil to lateral loads is slightly decreased. The Mononobe-Okabe static method is used to determine the equivalent fluid pressure.
- PPE = equivalent passive earth pressure during an earthquake
| Additional Information |
| 1992 AASHTO Div. IA Eqns. C6-5 and C6-6 |
- where:
- KPE = seismic passive pressure coefficient
- = unit weight of soil
- H = height of soil at the location where the earth pressure is to be found
- kV = vertical acceleration coefficient
- = angle of internal friction of soil
- kH = horizontal acceleration coefficient
- = slope of soil face in degrees
- i = backfill slope angle in degrees
- = angle of friction between soil and wall
Special Soil Conditions
Due to creep, some soft clay soils have no passive resistance under a continuing load. Removal of undesirable material and replacement with suitable material such as sand or crushed stone is necessary in such cases. Generally, this condition is indicated by a void ratio above 0.9, an angle of internal friction () less than 22°, or a soil shear less than 0.8 ksf. Soil shear is determined from a standard penetration test.
- Soil Shear
Friction
In the absence of tests, the total shearing resistance to lateral loads between the footing and a soil that derives most of its strength from internal friction may be taken as the normal force times a coefficient of friction. If the plane at which frictional resistance is evaluated is not below the frost line then this resistance must be neglected.
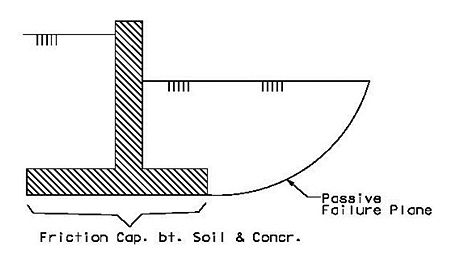
| Additional Information |
| AASHTO 5.5.2B |
Sliding is resisted by the friction force developed at the interface between the soil and the concrete footing along the failure plane. The coefficient of friction for soil against concrete can be taken from the table below. If soil data is not readily available or is inconsistent, the friction factor (f) can be taken as
- f = where is the angle of internal friction of the soil (Civil Engineering Reference Manual by Michael R. Lindeburg, 6th ed., 1992).
| Coefficient of Friction Values for Soil Against Concrete | |
|---|---|
| Soil Typea | Coefficient of Friction |
| coarse-grained soil without silt | 0.55 |
| coarse-grained soil with silt | 0.45 |
| silt (only) | 0.35 |
| clay | 0.30b |
| a It is not necessary to check rock or shale for sliding due to embedment. | |
| b Caution should be used with soils with < 22° or soil shear < 0.8 k/sq.ft. (soft clay soils). Removal and replacement of such soil with suitable material should be considered. | |
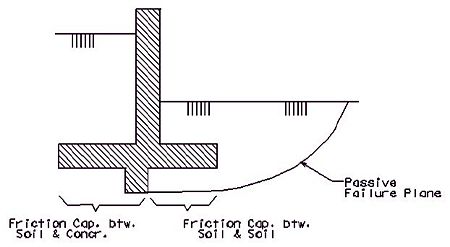
When a shear key is used, the failure plane is located at the bottom of the shear key in the front half of the footing. The friction force resisting sliding in front of the shear key is provided at the interface between the stationary layer of soil and the moving layer of soil, thus the friction angle is the internal angle of friction of the soil (soil against soil). The friction force resisting sliding on the rest of the footing is of that between the concrete and soil. Theoretically the bearing pressure distribution should be used to determine how much normal load exists on each surface, however it is reasonable to assume a constant distribution. Thus the normal load to each surface can be divided out between the two surfaces based on the fractional length of each and the total frictional force will be the sum of the normal load on each surface multiplied by the corresponding friction factor.
Bearing Pressure
| Additional Information |
| AASHTO 4.4.7.1.2 & 4.4.8.1.3 |
- Group Loads I - VI
- The bearing capacity failure factor of safety for Group Loads I - VI must be greater than or equal to 3.0. This factor of safety is figured into the allowable bearing pressure given on the "Design Layout Sheet".
- The bearing pressure on the supporting soil shall not be greater than the allowable bearing pressure given on the "Design Layout Sheet".
- Seismic Loads
| Additional Information |
| AASHTO Div. IA 6.3.1(B) and AASHTO 5.5.6.2 |
- When seismic loads are considered, AASHTO allows the ultimate bearing capacity to be used. The ultimate capacity of the foundation soil can be conservatively estimated as 2.0 times the allowable bearing pressure given on the "Design Layout".
- Stem Design
- The vertical stem (the wall portion) of a cantilever retaining wall shall be designed as a cantilever supported at the base.
- Footing Design
| Additional Information |
| AASHTO 5.5.6.1 |
- Toe
- The toe of the base slab of a cantilever wall shall be designed as a cantilever supported by the wall. The critical section for bending moments shall be taken at the front face of the stem. The critical section for shear shall be taken at a distance d (d = effective depth) from the front face of the stem.
- Heel
- The rear projection (heel) of the base slab shall be designed to support the entire weight of the superimposed materials, unless a more exact method is used. The heel shall be designed as a cantilever supported by the wall. The critical section for bending moments and shear shall be taken at the back face of the stem.
- Shear Key Design
- The shear key shall be designed as a cantilever supported at the bottom of the footing.
751.40.8.15.4.2 Pile Footings
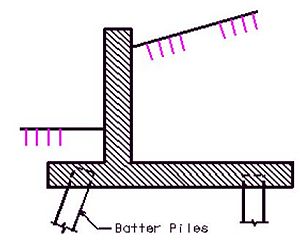
Footings shall be cast on piles when specified on the "Design Layout Sheet". If the horizontal force against the retaining wall cannot otherwise be resisted, some of the piles shall be driven on a batter.
- Pile Arrangement
- For retaining walls subject to moderate horizontal loads (walls 15 to 20 ft. tall), the following layout is suggested.
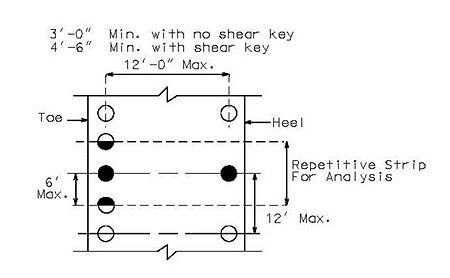
- For higher walls and more extreme conditions of loading, it may be necessary to:
- use the same number of piles along all rows
- use three rows of piles
- provide batter piles in more than one row
- Loading Combinations for Stability and Bearing
- The following table gives the loading combinations to be checked for stability and pile loads. These abbreviations are used in the table:
- DL = dead load weight of the wall elements
- SUR = two feet of live load surcharge
- E = earth weight
- EP = equivalent fluid earth pressure
- COL = collision force
- EQ = earthquake inertial force of failure wedge
| Loading Case | Vertical Loads | Horizontal Loads | Overturning Factor of Safety | Sliding Factor of Safety | |
|---|---|---|---|---|---|
| Battered Toe Piles | Vertical Toe Piles | ||||
| Ia | DL+SUR+E | EP+SUR | 1.5 | 1.5 | 2.0 |
| II | DL+SUR+E | EP+SUR+COL | 1.2 | 1.2 | 1.2 |
| III | DL+E | EP | 1.5 | 1.5 | 2.0 |
| IVb | DL+E | None | - | - | - |
| Vc | DL+E | EP+EQ | 1.125 | 1.125 | 1.5 |
| a Load Case I should be checked with and without the vertical surcharge. | |||||
| b A 25% overstress is allowed on the heel pile in Load Case IV. | |||||
| c The factors of safety for earthquake loading are 75% of that used in Load Case III. Battered piles are not recommended for use in seismic performance categories B, C, and D. Seismic design of retaining walls is not required in SPC A and B. Retaining walls in SPC B located under a bridge abutment shall be designed to AASHTO Specifications for SPC B. | |||||
- Pile Properties and Capacities
- For Load Cases I-IV in the table above, the allowable compressive pile force may be taken from the pile capacity table in the Piling Section of the Bridge Manual which is based in part on AASHTO 4.5.7.3. Alternatively, the allowable compressive pile capacity of a friction pile may be determined from the ultimate frictional and bearing capacity between the soil and pile divided by a safety factor of 3.5 (AASHTO Table 4.5.6.2.A). The maximum amount of tension allowed on a heel pile is 3 tons.
- For Load Case V in the table above, the allowable compressive pile force may be taken from the pile capacity table in the Piling Section of the Bridge Manual multiplied by the appropriate factor (2.0 for steel bearing piles, 1.5 for friction piles). Alternatively, the allowable compressive pile capacity of a friction pile may be determined from the ultimate frictional and bearing capacity between the soil and pile divided by a safety factor of 2.0. The allowable tension force on a bearing or friction pile will be equal to the ultimate friction capacity between the soil and pile divided by a safety factor of 2.0.
- To calculate the ultimate compressive or tensile capacity between the soil and pile requires the boring data which includes the SPT blow counts, the friction angle, the water level, and the soil layer descriptions.
- Assume the vertical load carried by battered piles is the same as it would be if the pile were vertical. The properties of piles may be found in the Piling Section of the Bridge Manual.
- Neutral Axis of Pile Group
- Locate the neutral axis of the pile group in the repetitive strip from the toe of the footing at the bottom of the footing.
- Moment of Inertia of Pile Group
- The moment of inertia of the pile group in the repetitive strip about the neutral axis of the section may be determined using the parallel axis theorem:
- I = Σ(IA) + Σ(Ad2) where :
- IA = moment of inertia of a pile about its neutral axis
- A = area of a pile
- d = distance from a pile's neutral axis to pile group's neutral axis
- IA may be neglected so the equation reduces to:
- I = Σ(Ad2)
- Resistance To Sliding
- Any frictional resistance to sliding shall be ignored, such as would occur between the bottom of the footing and the soil on a spread footing.
- Friction or Bearing Piles With Batter (Case 1)
- Retaining walls using friction or bearing piles with batter should develop lateral strength (resistance to sliding) first from the batter component of the pile and second from the passive pressure against the shear key and the piles.
- Friction or Bearing Piles Without Batter (Case 2)
- Retaining walls using friction or bearing piles without batter due to site constrictions should develop lateral strength first from the passive pressure against the shear key and second from the passive pressure against the pile below the bottom of footing. In this case, the shear key shall be placed at the front face of the footing.
- Concrete Pedestal Piles or Drilled Shafts (Case 3)
- Retaining walls using concrete pedestal piles should develop lateral strength first from passive pressure against the shear key and second from passive pressure against the pile below the bottom of the footing. In this case, the shear key shall be placed at the front of the footing. Do not batter concrete pedestal piles.
- Resistance Due to Passive Pressure Against Pile
- The procedure below may be used to determine the passive pressure resistance developed in the soil against the piles. The procedure assumes that the piles develop a local failure plane.
- F = the lateral force due to passive pressure on pile
- , where:
- = unit weight of soil
- H = depth of pile considered for lateral resistance (Hmax= 6B)
- CP = coefficient of active earth pressure
- B = width of pile
- = angle of internal friction of soil
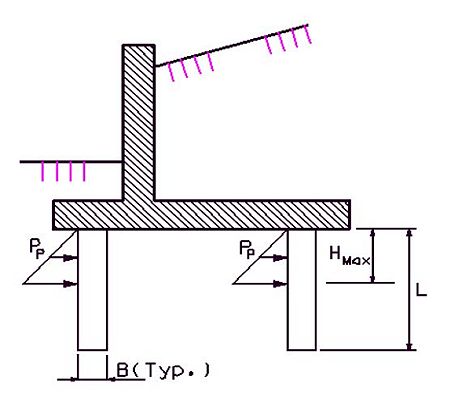
- Resistance Due to Pile Batter
- Use the horizontal component (due to pile batter) of the allowable pile load as the lateral resistance of the battered pile. (This presupposes that sufficient lateral movement of the wall can take place before failure to develop the ultimate strength of both elements.)
- b = the amount of batter per 12 inches.
- (# of battered piles) where:
- PHBatter = the horizontal force due to the battered piles
- PT = the allowable pile load
- Maximum batter is 4" per 12".
- Resistance Due to Shear Keys
- A shear key may be needed if the passive pressure against the piles and the horizontal force due to batter is not sufficient to attain the factor of safety against sliding. The passive pressure against the shear key on a pile footing is found in the same manner as for spread footings.
- Resistance to Overturning
- The resisting and overturning moments shall be computed at the centerline of the toe pile at a distance of 6B (where B is the width of the pile) below the bottom of the footing. A maximum of 3 tons of tension on each heel pile may be assumed to resist overturning. Any effects of passive pressure, either on the shear key or on the piles, which resist overturning, shall be ignored.
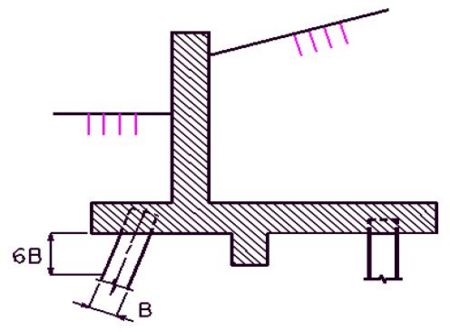
- Pile Properties
- Location of Resultant
- The location of the resultant shall be evaluated at the bottom of the footing and can be determined by the equation below:
- where:
- e = the distance between the resultant and the neutral axis of the pile group
- ΣM = the sum of the moments taken about the neutral axis of the pile group at the bottom of the footing
- ΣV = the sum of the vertical loads used in calculating the moment
- Pile Loads
- The loads on the pile can be determined as follows:
- where:
- P = the force on the pile
- A = the areas of all the piles being considered
- M = the moment of the resultant about the neutral axis
- c = distance from the neutral axis to the centerline of the pile being investigated
- I = the moment of inertia of the pile group
| Additional Information |
| AASHTO 5.5.6.2 |
- Stem Design
- The vertical stem (the wall portion) of a cantilever retaining wall shall be designed as a cantilever supported at the base.
- Footing Design
- Toe
| Additional Information |
| AASHTO 5.5.6.1 |
- The toe of the base slab of a cantilever wall shall be designed as a cantilever supported by the wall. The critical section for bending moments shall be taken at the front face of the stem. The critical section for shear shall be taken at a distance d (d = effective depth) from the front face of the stem.
- Heel
- The top reinforcement in the rear projection (heel) of the base slab shall be designed to support the entire weight of the superimposed materials plus any tension load in the heel piles (neglect compression loads in the pile), unless a more exact method is used. The bottom reinforcement in the heel of the base slab shall be designed to support the maximum compression load in the pile neglecting the weight of the superimposed materials. The heel shall be designed as a cantilever supported by the wall. The critical sections for bending moments and shear shall be taken at the back face of the stem.
- Shear Key Design
- The shear key shall be designed as a cantilever supported at the bottom of the footing.
751.40.8.15.4.3 Counterfort Walls
Assumptions:
(1) Stability The external stability of a counterfort retaining wall shall be determined in the same manner as described for cantilever retaining walls. Therefore refer to previous pages for the criteria for location of resultant, factor of safety for sliding and bearing pressures.
(2) Stem
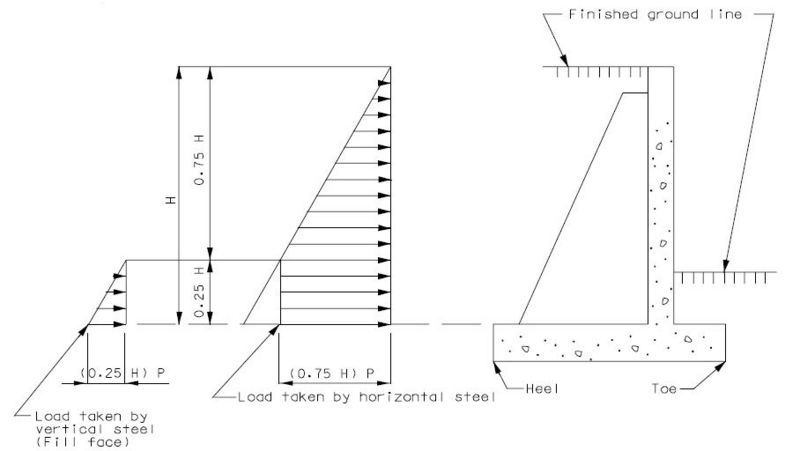
- where:
- Ca = coefficient of active earth pressure
- = unit weigt of soil
Design the wall to support horizontal load from the earth pressure and the liveload surcharge (if applicable) as outlined on the previous pages and as designated in AASHTD Section 3.20, except that maximum horizontal loads shall be the calculated equivalent fluid pressure at 3/4 height of wall [(0.75 H)P] which shall be considered applied uniformly from the lower quarter point to the bottom of wall.
In addition, vertical steel In the fill face of the bottom quarter of the wall shall be that required by the vertical cantilever wall with the equivalent fluid pressure of that (0.25 H) height.
Maximum concrete stress shall be assumed as the greater of the two thus obtained.
The application of these horizontal pressures shall be as follows:
(3) Counterfort Counterforts shall be designed as T-beams, of which the wall is the flange and the counterfort is the stem. For this reason the concrete stresses ane normally low and will not control.
For the design of reinforcing steel in the back of the counterfort, the effective d shall be the perpendicular distance from the front face of the wall (at point that moment is considered), to center of reinforcing steel.
(4) Footing
The footing of the counterfort walls shall be designed as a continuous beam of spans equal to the distance between the counterforts.
The rear projection or heel shall be designed to support the entire weight of the superimposed materials, unless a more exact method is used. Refer to AASHTD Section 5.5.6.
Divide footing (transversely) into four (4) equal sections for design footing pressures.
Counterfort walls on pile are very rare and are to be treated as special cases. See Structural Project Manager.
(5) Sign-Board type walls
The Sign-Board type of retaining walls are a special case of the counterfort retaining walls. This type of wall is used where the soiI conditions are such that the footings must be placed a great distance below the finished ground line. For this situation, the wall is discontinued approximately 12 in. below the finished ground line or below the frost line.
Due to the large depth of the counterforts, it may be more economical to use a smaller number of counterforts than would otherwise be used.
All design assumptions that apply to counterfort walls will apply to sign-board walls with the exception of the application of horizontal forces for the stem (or wall design), and the footing design which shall be as follows:
- Wall
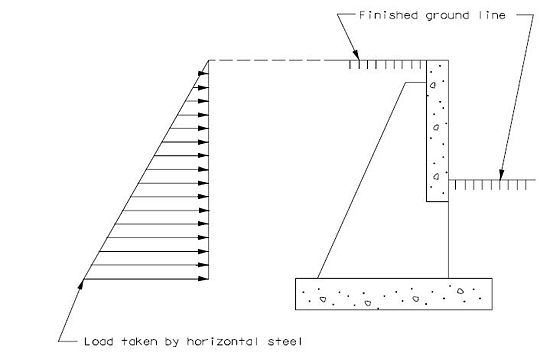
- Footing
- The individual footings shall be designed transversely as cantilevers supported by the wall. Refer to AASHTO Section 5.
751.40.8.15.5 Example 1: Spread Footing Cantilever Wall
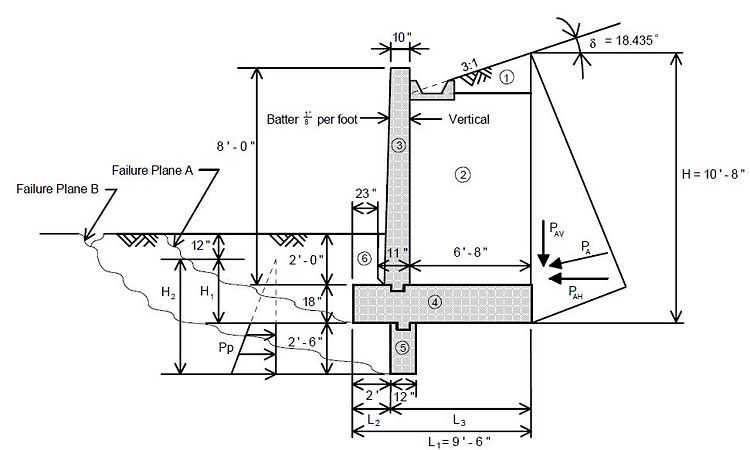
- f'c = 3,000 psi
- fy = 60,000 psi
- φ = 24 in.
- γs = 120 pcf (unit wgt of soil)
- Allowable soil pressure = 2 tsf
- γc = 150 pcf (unit wgt of concr.)
- Retaining wall is located in Seismic Performance Category (SPC) B.
- A = 0.1 (A = seismic acceleration coefficient)
Assumptions
- Retaining wall is under an abutment or in a location where failure of the wall may affect the structural integrity of a bridge. Therefore, it must be designed for SPC B.
- Design is for a unit length (1 ft.) of wall.
- Sum moments about the toe at the bottom of the footing for overturning.
- For Group Loads I-VI loading:
- F.S. for overturning ≥ 2.0 for footings on soil.
- F.S. for sliding ≥ 1.5.
- Resultant to be within middle 1/3 of footing.
- For earthquake loading:
- F.S. for overturning ≥ 0.75(2.0) = 1.5.
- F.S. for sliding ≥ 0.75(1.5) = 1.125.
- Resultant to be within middle 1/2 of footing.
- Base of footing is below the frost line.
- Neglect top one foot of fill over toe when determining passive pressure and soil weight.
- Use of a shear key shifts the failure plane to "B" where resistance to sliding is provided by passive pressure against the shear key, friction of soil along failure plane "B" in front of the key, and friction between soil and concrete along the footing behind the key.
- Soil cohesion along failure plane is neglected.
- Footings are designed as cantilevers supported by the wall.
- Critical sections for bending are at the front and back faces of the wall.
- Critical sections for shear are at the back face of the wall for the heel and at a distance d (effective depth) from the front face for the toe.
- Neglect soil weight above toe of footing in design of the toe.
- The wall is designed as a cantilever supported by the footing.
- Load factors for AASHTO Groups I - VI for design of concrete:
- γ = 1.3.
- βE = 1.3 for horizontal earth pressure on retaining walls.
- βE = 1.0 for vertical earth pressure.
- Load factor for earthquake loads = 1.0.
Lateral Pressures Without Earthquake
- Ca =
- Ca = = 0.546
| Load | Area (ft2) | Force (k) = (Unit Wgt.)(Area) | Arm (ft.) | Moment (ft-k) |
|---|---|---|---|---|
| (1) | (0.5)(6.667ft)(2.222ft) = 7.407 | 0.889 | 7.278 | 6.469 |
| (2) | (6.667ft)(6.944ft) = 46.296 | 5.556 | 6.167 | 34.259 |
| (3) | (0.833ft)(8.000ft) + (0.5)(0.083ft)(8.000ft) = 7.000 | 1.050 | 2.396 | 2.515 |
| (4) | (1.500ft)(9.500ft) = 14.250 | 2.138 | 4.750 | 10.153 |
| (5) | (2.500ft)(1.000ft) = 2.500 | 0.375 | 2.500 | 0.938 |
| (6) | (1.000ft)(1.917ft)+(0.5)(0.010ft)(1.000ft) = 1.922 | 0.231 | 0.961 | 0.222 |
| Σ | - | ΣV = 10.239 | - | ΣMR = 54.556 |
| PAV | - | 1.178 | 9.500 | 11.192 |
| Σ resisting | - | ΣV = 11.417 | - | ΣMR = 65.748 |
| PAH | - | 3.534 | 3.556 | 12.567 |
| PP | - | 2.668 | 1.3891 | - |
| 1 The passive capacity at the shear key is ignored in overturning checks,since this capacity is considered in the factor of safety against sliding. It is assumed that a sliding and overturning failure will not occur simultaneously. The passive capacity at the shear key is developed only if the wall does slide. | ||||
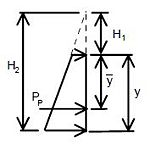
= 1.389 ft.
- Overturning
- F.S. = o.k.
- where: MOT = overturning moment; MR = resisting moment
- Resultant Eccentricity
- = 4.658 ft.
- o.k.
- Sliding
- Check if shear key is required for Group Loads I-VI:
- F.S. = = 0.896 no good - shear key req'd
- where: φs-c = angle of friction between soil and concrete = (2/3)φs-s
- F.S. =
- where: φs-s = angle of internal friction of soil
- F.S. = = 1.789 ≥ 1.5 o.k.
- Footing Pressure
- PH = pressure at heel = 1.132 k/ft2
- PT = pressure at toe = 1.272 k/ft2
- Allowable pressure = 2 tons/ft2 = 4 k/ft2 ≥ 1.272 k/ft2 o.k.
Lateral Pressures With Earthquake
kh = 0.5A = 0.5 (0.1) = 0.05
kv = 0
- Active Pressure on Psuedo-Wall
- δ = φ = 24° (δ is the angle of friction between the soil and the wall. In this case, δ = φ = because the soil wedge considered is next to the soil above the footing.)
- i = 18.435°
- β = 0°
- KAE = 0.674
- PAE = ½γsH2(1 − kv)KAE
- PAE = ½[0.120 k/ft3](10.667 ft)2(1 ft.)(1 - 0)(0.674) = 4.602k
- PAEV = PAE(sinδ) = 4.602k(sin24°) = 1.872k
- PAEH = PAE(cosδ) = 4.602k(cos 24°) = 4.204k
- P'AH = PAEH − PAH = 4.204k − 3.534k = 0.670k
- P'AV = PAEV − PAV = 1.872k − 1.178k = 0.694k
- where: P'AH and P'AV are the seismic components of the active force.
- Passive Pressure on Shear Key
- δ = φ = 24° (δ = φ because the soil wedge considered is assumed to form in front of the footing.)
- i = 0
- β = 0
- KPE = 0.976
- PPE = ½γsH2(1 − kv)KPE
- PPE = ½[0.120 k/ft3][(5.0 ft)2 - (2.5 ft2)](1 ft.)(1 - 0)(0.976) = 1.098k
| Load | Force (k) | Arm (ft) | Moment (ft-k) |
|---|---|---|---|
| Σ (1) thru (6) | 10.239 | - | 54.556 |
| PAV | 1.178 | 9.500 | 11.192 |
| P'AV | 0.694 | 9.500 | 6.593 |
| Σresisting | ΣV = 12.111 | - | ΣMR = 72.341 |
| PAH | 3.534 | 3.556 | 12.567 |
| P'AH | 0.670 | 6.400a | 4.288 |
| PPEV | 0.447b | 0.000 | 0.000 |
| PPEH | 1.003b | 1.389c | 0.000 |
| - | - | - | ΣMOT = 16.855 |
| a P'AH acts at 0.6H of the wedge face (1992 AASHTO Div. IA Commentary). | |||
| b PPEH and PPEH are the components of PPE with respect to δ (the friction angle). PPE does not contribute to overturning. | |||
| c The line of action of PPEH can be located as was done for PP. | |||
- Overturning
- o.k.
- Resultant Eccentricity
- o.k.
- Sliding
- o.k.
- Footing Pressure
- for e ≤ L/6:
- = 1.139 k/ft2
- = 1.411 k/ft2
- Allowable soil pressure for earthquake = 2 (allowable soil pressure)
- (2)[4 k/ft2] = 8 k/ft2 > 1.411 k/ft2 o.k.
Reinforcement-Stem
d = 11" - 2" - (1/2)(0.5") = 8.75"
b = 12"
f'c = 3,000 psi
- Without Earthquake
- PAH = ½ [0.120 k/ft3](0.546)(6.944 ft.)2(1 ft.)(cos 18.435°) = 1.499k
- γ = 1.3
- βE = 1.3 (active lateral earth pressure)
- Mu = (1.3)(1.3)(1.499k)(2.315ft) = 5.865 (ft-k)
- With Earthquake
- kh = 0.05
- kv = 0
| Additional Information |
| 1992 AASHTO Div. IA Commentary |
- θ = 2.862°
- δ = φ/2 = 24°/2 = 12° for angle of friction between soil and wall. This criteria is used only for seismic loading if the angle of friction is not known.
- φ = 24°
- i = 18.435°
- β = 0°
- KAE = 0.654
- PAEH = 1/2 γsKAEH2cosδ
- PAEH = 1/2 [0.120k/ft](0.654)(6.944 ft.)2(1 ft.) cos(12°) = 1.851k
- Mu = (1.499k)(2.315 ft.) + (1.851k − 1.499k)(0.6(6.944 ft.)) = 4.936(ft−k)
- The moment without earthquake controls:
- = 85.116 psi
- ρ =
- ρ = = 0.00144
| Additional Information |
| AASHTO 8.17.1.1 & 8.15.2.1.1 |
- ρmin = = 0.00245
- Use ρ = 4/3 ρ = 4/3 (0.00144) = 0.00192
- ASReq = ρbd = 0.00192 (12 in.)(8.75 in.) = 0.202 in.2/ft
- One #4 bar has AS = 0.196 in2
- s = 11.64 in.
- Use #4's @ 10" cts.
- Check Shear
- Vu ≥ φ Vn
- Without Earthquake
- Vu, = (1.3)(1.3)(1.499k) = 2.533k
- With Earthquake
- Vu = 1.851k
- The shear force without earthquake controls.
- = 28.4 psi
- = 109.5 psi > 28.4 psi o.k.
Reinforcement-Footing-Heel
Note: Earthquake will not control and will not be checked.
βE = 1.0 (vertical earth pressure)
d = 18" - 3" - (1/2)(0.750") = 14.625"
b = 12"
f'c = 3,000 psi
Mu = 1.3 [(5.556k + 1.500k)(3.333ft) + 0.889k(4.444ft) + 1.178k(6.667ft)]
Mu = 45.919(ft−k)
= 238.5 psi
ρ = = 0.00418
ρmin = = 0.00235
ASReq = 0.00418 (12 in.) (14.625 in.) = 0.734 in2/ft.
Use #6's @ 7" cts.
- Check Shear
- Shear shall be checked at back face of stem.
- Vu = 1.3 (5.556k + 1.500k + 0.889k + 1.178k) = 11.860k
- = 109.5 psi o.k.
Reinforcement-Footing-Toe
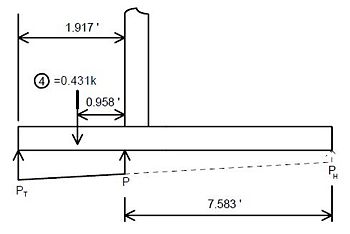
d = 18" - 4" = 14"
b = 12"
- Without Earthquake
- Apply Load Factors
- load 4 (weight) = 0.431k(1.3)(1.0) = 0.560k
- βE = 1.3 for lateral earth pressure for retaining walls.
- βE = 1.0 for vertical earth pressure.
- ΣMOT = 12.567(ft−k)(1.3)(1.3) = 21.238(ft−k)
- ΣMR = [54.556(ft−k) + 11.192(ft−k)](1.3)(1.0) = 85.472(ft−k)
- ΣV = 11.417k(1.3)(1.0) = 14.842k
- = 4.328 ft.
- e = (9.5 ft./2) − 4.328 ft. = 0.422 ft.
- = 1.146k/ft2
- = 1.979k/ft2
- = 1.811k/ft.
- Mu = 2.997(ft−k)
- With Earthquake
- PH = 1.139 k/ft
- PT = 1.411 k/ft
- = 1.356 k/ft
- Mu = 2.146(ft−k)
- The moment without earthquake controls.
- = 16.990 psi
- ρ = = 0.000284
- ρmin = = 0.00257
- Use ρ = 4/3 ρ = = 0.000379
- ASReq = 0.000379 (12 in.)(14.0 in.) = 0.064 in.2/ft.
- s = 36.8 in.
- Minimum is # 4 bars at 12 inches. These will be the same bars that are in the back of the stem. Use the smaller of the two spacings.
- Use # 4's @ 10" cts.
- Check Shear
- Shear shall be checked at a distance "d" from the face of the stem.
- Without Earthquake
- = 1.913k/ft.
- = 1.240k
- With Earthquake
- = 1390k/ft.
- = 0.788k
- Shear without earthquake controls.
- = 109.5 psi o.k.
Reinforcement-Shear Key
The passive pressure is higher without earthquake loads.
γ = 1.3
βE = 1.3 (lateral earth pressure)
d = 12"-3"-(1/2)(0.5") = 8.75"
b = 12"
Mu = (3.379k)(1.360 ft.)(1.3)(1.3) = 7.764(ft−k)
= 112.677 psi
ρ = = 0.00192
ρmin = = 0.00292
Use ρ = 4/3 ρ = 4/3 (0.00192) = 0.00256
ASReq = 0.00256(12 in.)(8.75 in.) = 0.269 in.2/ft.
Use # 4 @ 8.5 in cts.
Check Shear
- = 109.5 psi o.k.
Reinforcement Summary
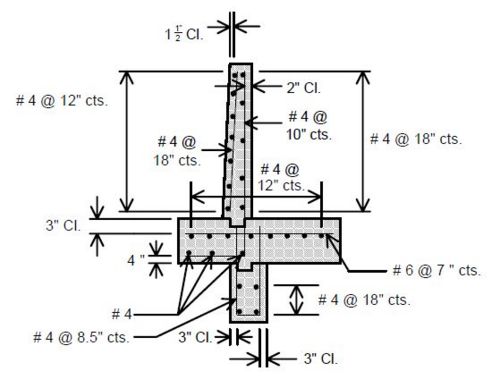
751.40.8.15.6 Example 2: L-Shaped Cantilever Wall
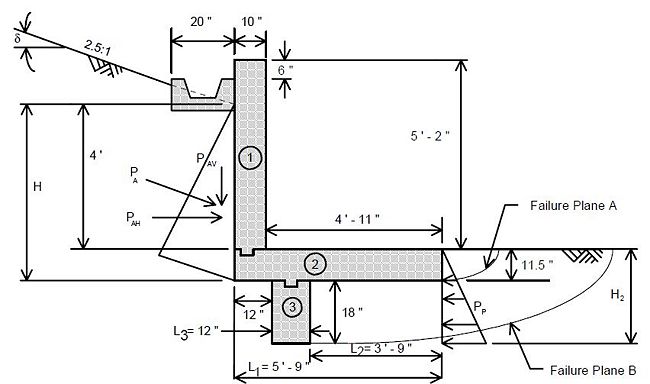
f'c = 4000 psi
fy = 60,000 psi
φ = 29°
γs = 120 pcf
Allowable soil pressure = 1.5 tsf = 3.0 ksf
Retaining wall is located in Seismic Performance Category (SPC) A.
= 21.801°
= 0.462
= 2.882
PA = 1/2 γs CaH2 = 1/2 (0.120 k/ft3)(0.462)(4.958 ft.)2 = 0.681k
For sliding, PP is assumed to act only on the portion of key below the frost line that is set at an 18 in. depth on the southern border.
PP = 1/2 (0.120 k/ft3)(2.882)[(2.458 ft.)2 − (1.500 ft.)2] = 0.656k
Assumptions
- Design is for a unit length (1 ft.) of wall.
- Sum moments about the toe at the bottom of the footing for overturning.
- F.S. for overturning ≥ 2.0 for footings on soil.
- F.S. for sliding ≥ 1.5 for footings on soil.
- Resultant of dead load and earth pressure to be in back half of the middle third of the footing if subjected to frost heave.
- For all loading combinations the resultant must be in the middle third of the footing except for collision loads.
- The top 12 in. of the soil is not neglected in determining the passive pressure because the soil there will be maintained.
- Frost line is set at 18 in. at the south border for Missouri.
- Portions of shear key which are above the frost line are assumed not to resist sliding by passive pressure.
- Use of a shear key shifts the failure plane to "B" where resistance to sliding is also provided by friction of soil along the failure plane in front of the shear key. Friction between the soil and concrete behind the shear key will be neglected.
- Soil cohesion along the failure plane is neglected.
- Live loads can move to within 1 ft. of the stem face and 1 ft. from the toe.
- The wall is designed as a cantilever supported by the footing.
- Footing is designed as a cantilever supported by the wall. Critical sections for bending and shear will be taken at the face of the wall.
- Load factors for AASHTO Groups I-VI for design of concrete are:
- γ = 1.3.
- βE = 1.3 for horizontal earth pressure on retaining walls.
- βE = 1.0 for vertical earth pressure.
- βLL = 1.67 for live loads and collision loads.
Dead Load and Earth Pressure - Stabilty and Pressure Checks
| Dead Load and Earth Pressure - Stabilty and Pressure Checks | |||
|---|---|---|---|
| Load | Force (k) | Arm (in.) | Moment (ft-k) |
| (1) | (0.833 ft.)(5.167 ft.)(0.150k/ft3) = 0.646 | 5.333 | 3.444 |
| (2) | (0.958ft)(5.750ft)(0.150k/ft3) = 0.827 | 2.875 | 2.376 |
| (3) | (1.000ft)(1.500ft)(0.150k/ft3) = 0.22534.259 | 4.250 | 0.956 |
| ΣV = 1.698 | ΣMR = 6.776 | ||
| PAV | 0.253 | 5.750 | 1.455 |
| ΣV = 1.951 | ΣMR = 8.231 | ||
| PAH | 0.633 | 1.653 | 1.045 |
| PP | 0.656 | 1.061 | - |
| ΣMOT = 1.045 | |||
| 1 The passive pressure at the shear key is ignored in overturning checks. | |||
- Overturning
- = 7.877 ≥ 2.0 o.k.
- Location of Resultant
- MoDOT policy is that the resultant must be in the back half of the middle third of the footing when considering dead and earth loads:
- = 3.683 ft. o.k.
- Sliding
- where:
- φs-s = angle of internal friction of soil
- φs-c = angle of friction between soil and concrete = (2/3)φs-s
- = 2.339 ≥ 1.5 o.k.
- Footing Pressure
- = 0.808 ft.
- Heel: = 0.625 ksf < 3.0 ksf o.k.
- Toe: = 0.053 ksf < 3.0 ksf o.k.
Dead Load, Earth Pressure, and Live Load - Stability and Pressure Checks
Stability is not an issue because the live load resists overturning and increases the sliding friction force.
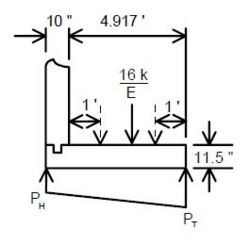
The live load will be distributed as:
- where E = 0.8X + 3.75
- X = distance in feet from the load to the front face of wall
The live load will be positioned as shown by the dashed lines above. The bearing pressure and resultant location will be determined for these two positions.
- Live Load 1 ft From Stem Face
- Resultant Eccentricity
- X = 1 ft.
- E = 0.8(1 ft.) + 3.75 = 4.55 ft.
- = 3.516k
- = 3.834 ft.
- = 5.75 ft. o.k.
- Footing Pressure
- Allowable Pressure = 3.0 ksf
- Heel: = 1.902 ksf
- Toe: = 0.000ksf
- Live Load 1 ft From Toe
- Resultant Eccentricity
- X = 3.917 ft.
- E = 0.8(3.917 ft.) + 3.75 = 6.883 ft.
- = 2.324k
- = 2.225 ft.
- = 0.958 ft. o.k.
- Footing Pressure
- Allowable Pressure = 3.0ksf
- Heel: = 0.239ksf o.k.
- Toe: = 1.248ksf o.k.
Dead Load, Earth Pressure, Collision Load, and Live Load - Stability and Pressure Checks
During a collision, the live load will be close to the wall so check this combination when the live load is one foot from the face of the stem. Sliding (in either direction) will not be an issue. Stability about the heel should be checked although it is unlikely to be a problem. There are no criteria for the location of the resultant, so long as the footing pressure does not exceed 125% of the allowable. It is assumed that the distributed collision force will develop an equal and opposite force on the fillface of the back wall unless it exceeds the passive pressure that can be developed by soil behind the wall.
FLL = 3.516k
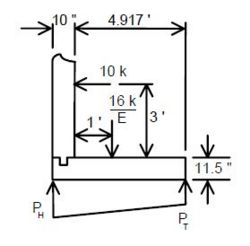
FCOLL = = 1.667k
= 1.867
PPH = 2.556k > FCOLL Thus the soil will develop an equal but opp. force.
- Overturning About the Heel
- F.S. =
- F.S. = = 1.847 ≥ 1.2 o.k.
- Footing Pressure
- = 1.022 ft. from heel
- e = = 1.853 ft.
- Allowable Pressure = (1.25)(3.0ksf) = 3.75ksf
- Heel: = 3.566ksf o.k.
Stem Design-Steel in Rear Face
γ = 1.3
βE = 1.3 (active lateral earth pressure)
d = 10 in. − 2 in. − (0.5 in./2) = 7.75 in.
PAH = 0.412k
Mu = (1.333 ft.)(0.412k)(1.3)(1.3) = 0.928(ft−k)
= 17.160psi
= 0.000287
= 0.00298
Use ρ = (4/3)ρ = (4/3)(0.000287) = 0.000382
One #4 bar has AS = 0.196 in2, so the required minimum of one #4 bar every 12 in. controls.
Use #4's @ 12 in. (min)
(These bars are also the bars in the bottom of the footing so the smaller of the two required spacings will be used.)
- Check Shear
- = 8.8 psi
- = 126.5 psi > 8.8 psi o.k.
Stem Design-Steel in Front Face (Collision Loads)
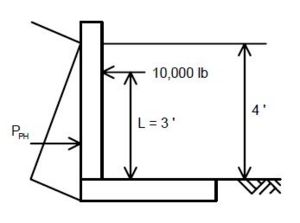
The soil pressure on the back of the stem becomes passive soil pressure during a collision, however this pressure is ignored for reinforcement design.
γ = 1.3
βLL = 1.67
= 7.75 in.
= 1.667 k/ft.
Mu = 1.667k/ft. (1 ft.)(3 ft.)(1.3)(1.67) = 10.855(ft−k)
= 200.809 psi
= 0.00345
= 0.00298
One #4 bar has AS = 0.196 in2.
s = 7.3 in.
Use #4's @ 7 in.
- Check Shear
- = 45.8 psi < 126.5 psi o.k.
Footing Design - Bottom Steel
It is not considered necessary to design footing reinforcement based upon a load case which includes collision loads.
- Dead Load and Earth Pressure Only
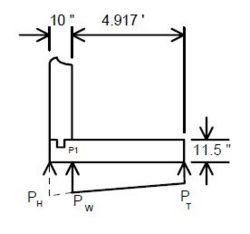
- Footing wt. = = 0.707k
- βE = 1.3 (lateral earth pressure)
- γ = 1.3
- Apply Load Factors:
- ΣV = 1.951k (1.3) = 2.536k
- ΣMR = 8.231(ft−k)(1.3) = 10.700(ft−k)
- ΣMOT = 1.045(ft−k)(1.3)(1.3) = 1.766(ft−k)
- Footing wt. = 0.707k (1.3) = 0.919k
- = 3.523 ft.
- = 0.648 ft.
- = 0.739 ksf
- = 0.143ksf
- = 0.653 ksf
- Moment at Wall Face:
- = 1.524(ft−k)
- Dead Load, Earth Pressure, and Live Load
- Live Load 1 ft. From Stem Face
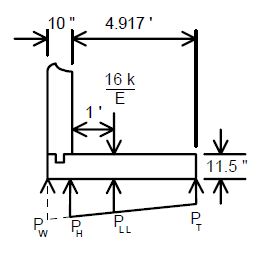
- βE = 1.3 (lateral earth pressure)
- βLL = 1.67
- γ = 1.3
- Apply Load Factors:
- FLL = 3.516k(1.3)(1.67) = 7.633k
- ΣV = 7.633k + 1.951k(1.3) = 10.169k
- ΣMOT = 1.045(ft−k)(1.3)(1.3) = 1.766(ft−k)
- ΣMR = 8.231(ft−k)(1.3) + 3.917 ft.(7.633k) = 40.599(ft−k)
- = 3.819 ft.
- e = 3.819 ft. − (5.75 ft./2) = 0.944 ft.
- = 0.026 ksf
- = 3.511 ksf
- = 3.006 ksf
- = 2.400 ksf
- Footing wt. from face of wall to toe:
- Footing wt. = = 0.919k
- Footing wt. from LLWL to toe:
- Footing wt. = = 0.732k
- Moment at Wall Face:
- MW =
- MW = 2.430(ft−k)
- Moment at LLWL:
- MLL = = 4.837(ft−k)
- Live Load 1 ft. From Toe
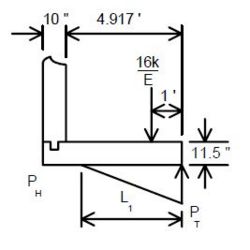
- Apply Load Factors:
- FLL = 2.324k(1.3)(1.67) = 5.045k
- ΣV = 5.045k + 1.951k(1.3) = 7.581k
- ΣMOT = 1.045(ft−k)(1.3)(1.3) = 1.766(ft−k)
- ΣMR = 8.231(ft−k)(1.3) + 5.045k(1ft.) = 15.745(ft−k)
- = 1.844 ft.
- = 1.031 ft.
- PH = 0 ksf
- = 2.741 ksf
- L1 = 3[(L/2)− e]
- L1 = 3[(5.75 ft./2)− 1.031 ft.] = 5.532 ft.
- = 0.305 ksf
- = 2.196 ksf
- Moment at Wall Face:
- MW = = 1.298(ft−k)
- Moment at LLWL:
- MLL = = 1.186(ft−k)
- Design Flexural Steel in Bottom of Footing
- d = 11.5 in. − 4 in. = 7.500 in.
- Mu = 4.837(ft−k) (controlling moment)
- = 0.096 ksi
- = 0.00162
- = 0.00421
- Use ρ = (4/3)ρ = (4/3)(0.00162) = 0.00216
- ASReq = 0.00216(12 in.)(7.5 in.) = 0.194 in2/ft.
- s = 12.1 in.
- Use #4's @ 12 in. cts. (Also use this spacing in the back of the stem.)
- Check Shear
- Dead Load and Earth Pressure Only
- VW = 1.038k
- Live Load 1 ft. From Stem Face
- Shear at the wall can be neglected for this loading case.
- VLL = 4.019k
- Live Load 1 ft. From Toe
- VW = 1.525k
- VLL = 2.282k
- Use VU = 4.019k
- = 126.5 psi
Shear Key Design
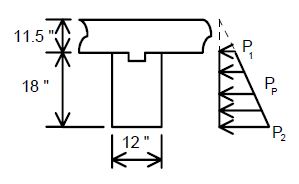
For concrete cast against and permanently exposed to earth, minimum cover for reinforcement is 3 inches.
= 8.75 in.
= 0.331 k/ft.
= 0.850 k/ft.
Mu = 1.287(ft−k)
= 0.0187 ksi
= 0.000312
= 0.00337
Use ρ = (4/3)ρ = (4/3)(0.000312) = 0.000416
ASReq = 0.000416 (12 in.)(8.75 in.) = 0.0437 in2/ft.
s = 53.8 in.
Use #4's @ 18 in. cts. (min)
- Check Shear
- V = 0.886k
- = 16.8 psi < 126.5 psi o.k.
Reinforcement Summary
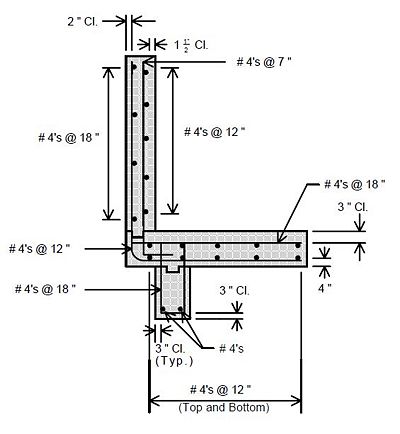
751.40.8.15.7 Example 3: Pile Footing Cantilever Wall
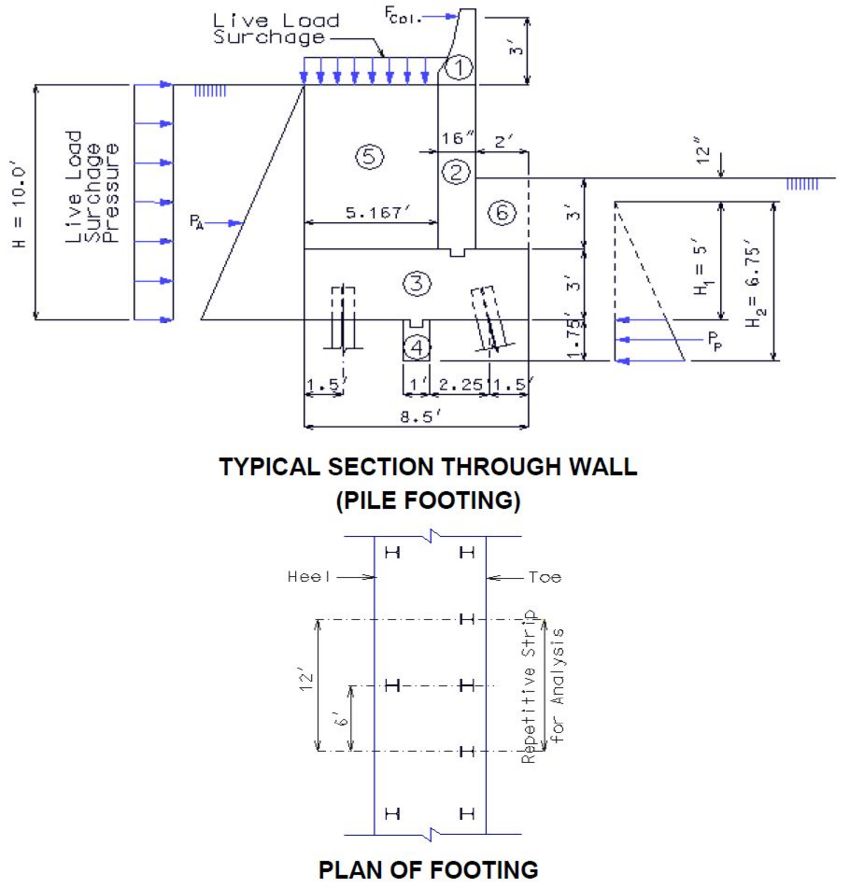
f’c = 3,000 psi
fy = 60,000 psi
φ = 27°
γs = 120 pcf
Pile type: HP 10 x 42
Allowable pile bearing = 56 tons
Pile width = 10 inches
Toe pile batter = 1:3
See EPG 751.12 Barriers, Railings, Curbs and Fences for weight and centroid of barrier.
Assumptions
- Retaining wall is located such that traffic can come within half of the wall height to the plane where earth pressure is applied.
- Reinforcement design is for one foot of wall length.
- Sum moments about the centerline of the toe pile at a distance of 6B (where B is the pile width) below the bottom of the footing for overturning.
- Neglect top one foot of fill over toe in determining soil weight and passive pressure on shear key.
- Neglect all fill over toe in designing stem reinforcement.
- The wall is designed as a cantilever supported by the footing.
- Footing is designed as a cantilever supported by the wall.
- Critical sections for bending are at the front and back faces of the wall.
- Critical sections for shear are at the back face of the wall for the heel and at a distance d (effective depth) from the front face for the toe.
- For load factors for design of concrete, see EPG 751.24.1.2 Group Loads.
δ = 0, ϕ = 27° so CA reduces to:
= 0.376
= 2.663
Table 751.24.3.5.1 is for stability check (moments taken about C.L. of toe pile at a depth of 6B below the bottom of the footing).
| Load | Force (kips/ft) | Arm about C.L. of toe pile at 6B below footing (ft.) | Moment (ft-kips) per foot of wall length | |
|---|---|---|---|---|
| Dead Load | (1) | 0.340 | 2.542 | 0.864 |
| (2) | (1.333 ft.)(7.000 ft.)(0.150k/ft3) = 1.400 | 2.833 | 3.966 | |
| (3) | (3.000 ft.)(8.500 ft.)(0.150k/ft3) = 3.825 | 4.417 | 16.895 | |
| (4) | (1.000 ft.)(1.750 ft.)(0.150k/ft3) = 0.263 | 4.417 | 1.162 | |
| Σ | ΣV = 5.828 | - | ΣMR = 22.887 | |
| Earth Load | (5) | (7.000 ft.)(5.167 ft.)(0.120k/ft3) = 4.340 | 6.083 | 26.400 |
| (6) | (2.000 ft.)(2.000 ft.)(0.120k/ft3) = 0.480 | 1.167 | 0.560 | |
| Σ | ΣV = 4.820 | - | ΣMR = 26.960 | |
| Live Load Surcharge | PSV | (2.000 ft.)(5.167 ft.)(0.120k/ft3) = 1.240 | 6.083 | MR = 7.543 |
| PSH | (2.000 ft.)(0.376)(10.000 ft.)(0.120k/ft3) = 0.902 | 10.000 | MOT = 9.020 | |
| Earth Pressure | PA | 2.2561 | 8.333 | MOT = 18.799 |
| PP | 3.2852 | - | - | |
| Collision Force (FCOL) | (10.000k)/[2(7.000 ft.)] = 0.714 | 18.000 | MOT = 12.852 | |
| Heel Pile Tension (PHV) | (3.000 tons)(2 k/ton)(1 pile)/(12.000 ft.) = 0.500 | 7.167 | MR = 3.584 | |
| Toe Pile Batter (PBH) | 5.9033 | - | - | |
| Passive Pile Pressure (Ppp) | 0.8324 | - | - | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
Table 751.24.3.5.2 is for bearing pressure checks (moments taken about C.L of toe pile at the bottom of the footing).
| Load | Force (kips/ft) | Arm about C.L. of toe pile at 6B below footing (ft.) | Moment (ft-kips) per foot of wall length | |
|---|---|---|---|---|
| Dead Load | (1) | 0.340 | 0.875 | 0.298 |
| (2) | (1.333 ft.)(7.000 ft.)(0.150k/ft3) = 1.400 | 1.167 | 1.634 | |
| (3) | (3.000 ft.)(8.500 ft.)(0.150k/ft3) = 3.825 | 2.750 | 10.519 | |
| (4) | (1.000 ft.)(1.750 ft.)(0.150k/ft3) = 0.263 | 2.750 | 0.723 | |
| Σ | ΣV = 5.828 | - | ΣMR = 13.174 | |
| Earth Load | (5) | (7.000 ft.)(5.167 ft.)(0.120k/ft3) = 4.340 | 4.417 | 19.170 |
| (6) | (2.000 ft.)(2.000 ft.)(0.120k/ft3) = 0.480 | -0.500 | -0.240 | |
| Σ | ΣV = 4.820 | - | ΣMR = 18.930 | |
| Live Load Surcharge | PSV | (2.000 ft.)(5.167 ft.)(0.120k/ft3) = 1.240 | 4.417 | MR = 5.477 |
| PSH | (2.000 ft.)(0.376)(10.000 ft.)(0.120k/ft3) = 0.902 | 5.000 | MOT = 4.510 | |
| Earth Pressure | PA | 2.256 | 3.333 | MOT = 7.519 |
| PP | 3.285 | - | - | |
| Collision Force (FCOL) | (10.000k)/[2(7.000 ft.)] = 0.714 | 13.000 | MOT = 9.282 | |
| Heel Pile Tension (PHV) | (3.000 tons)(2 k/ton)(1 pile)/(12.000 ft.) = 0.500 | 5.500 | MR = 2.750 | |
| Toe Pile Batter (PBH) | 5.903 | - | - | |
| Passive Pile Pressure (Ppp) | 0.832 | - | - | |
Investigate a representative 12 ft. strip. This will include one heel pile and two toe piles. The assumption is made that the stiffness of a batter pile in the vertical direction is the same as that of a vertical pile.
Neutral Axis Location = [2piles(1.5 ft.) + 1pile(7 ft.)] / (3 piles) = 3.333 ft. from the toe.
I = Ad2
For repetitive 12 ft. strip:
- Total pile area = 3A
- I = 2A(1.833 ft.)2 + A(3.667 ft.)2 = 20.167(A)ft.2
For a 1 ft. unit strip:
- Total pile area = (3A/12 ft.) = 0.250A
- Case I
- F.S. for overturning ≥ 1.5
- F.S. for sliding ≥ 1.5
- Check Overturning
- Neglect resisting moment due to PSV for this check.
- ΣMR = 22.887(ft−k) + 26.960(ft−k) + 3.584(ft−k)
- ΣMR = 53.431(ft−k)
- ΣMOT = 9.020(ft−k) + 18.799(ft−k) = 27.819(ft−k)
- F.S.OT = = 1.921 > 1.5 o.k.
- Check Pile Bearing
- Without PSV :
- ΣV = 5.828k + 4.820k = 10.648k
- e = = 1.885 ft.
- Moment arm = 1.885 ft. - 1.833 ft. = 0.052 ft.
- Allowable pile load = 56 tons/pile. Each pile has area A, so:
- o.k.
- o.k.
- With PSV:
- ΣV = 5.828k + 4.820k + 1.240k = 11.888k
- = 2.149 ft.
- Moment arm = 2.149 ft. - 1.833 ft. = 0.316 ft.
- o.k.
- o.k.
- Check Sliding
- = 3.173 ≥ 1.5 o.k.
- Case II
- F.S. for overturning ≥ 1.2
- F.S. for sliding ≥ 1.2
- Check Overturning
- ΣMR = (22.887 + 26.960 + 7.543 + 3.584)(ft−k) = 60.974(ft−k)
- ΣMOT = (9.020 + 18.799 + 12.852)(ft−k) = 40.671(ft−k)
- = 1.499 ≥ 1.2 o.k.
- Check Pile Bearing
- = 1.369 ft.
- Moment arm = 1.833 ft. - 1.369 ft. = 0.464 ft.
- o.k.
- = 35.519k
- o.k.
- Check Sliding
- = 2.588 ≥ 1.2 o.k.
- Case III
- F.S. for overturning ≥ 1.5
- F.S. for sliding ≥ 1.5
- Check Overturning
- ΣMR = (22.887 + 26.960 + 3.584)(ft−k) = 53.431(ft−k)
- ΣMOT = 18.799(ft−k)
- = 2.842 ≥ 1.5 o.k.
- Check Pile Bearing
- = 2.309 ft.
- Moment arm = 2.309 ft. - 1.833 ft. = 0.476 ft.
- = 37.065k
- o.k.
- = 53.649k
- o.k.
- Check Sliding
- = 4.441 ≥ 1.5 o.k.
- Case IV
- Check Pile Bearing
- = 3.015 ft.
- Moment arm = 3.015 ft. - 1.833 ft. = 1.182 ft.
- 25% overstress is allowed on the heel pile:
- o.k.
- = 28.868k
- o.k.
- Reinforcement - Stem
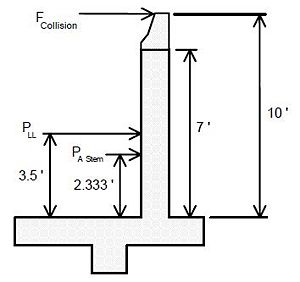
- b = 12 in.
- cover = 2 in.
- h = 16 in.
- d = 16 in. - 2 in. - 0.5(0.625 in.) = 13.688 in.
- FCollision = 0.714k/ft
- Apply Load Factors
- FCol. = γβLL(0.714k) = (1.3)(1.67)(0.714k) = 1.550k
- PLL = γβE (0.632k) = (1.3)(1.67)(0.632k) = 1.372k
- PAStem = γβE (1.105k) = (1.3)(1.3)(1.105k) = 1.867k
- Mu = (10.00 ft.)(1.550k) + (3.500 ft.)(1.372k) + (2.333 ft.)(1.867k)
- Mu = 24.658(ft−k)
- = 0.146ksi
- = 0.00251
- = 0.00212
- ρ = 0.00251
- One #5 bar has AS = 0.307 in2
- s = 8.9 in.
- Use # 5 bars @ 8.5 in. cts.
- Check Shear
- Vu ≤ φVn
- Vu = FCollision + PLL + PAStem = 1.550k + 1.372k + 1.867k = 4.789k
- = 34.301 psi
- = 109.5 psi > 34.3 psi o.k.
- Reinforcement - Footing - Top Steel
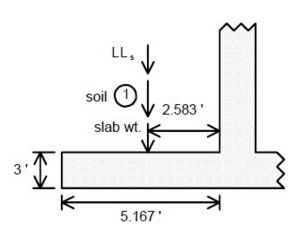
- b = 12 in.
- cover = 3 in.
- h = 36 in.
- d = 36 in. - 3 in. - 0.5(0.5 in.) = 32.750 in.
- Design the heel to support the entire weight of the superimposed materials.
- Soil(1) = 4.340k/ft.
- LLs = 1.240k/ft.
- = 2.325k/ft.
- Apply Load Factors
- Soil(1) = γβE(4.340k) = (1.3)(1.0)(4.340k) = 5.642k
- LLs = γβE(1.240k) = (1.3)(1.67)(1.240k) = 2.692k
- Slab wt. = γβD(2.325k) = (1.3)(1.0)(2.325k) = 3.023k
- Mu = (2.583 ft.)(5.642k + 2.692k + 3.023k) = 29.335(ft−k)
- = 0.0304 ksi
- = 0.000510
- = 0.00188
- Use ρ = 4/3 ρ = 4/3 (0.000510) = 0.000680
- One #4 bar has As = 0.196 in.2
- s = 8.8 in.
- Use #4 bars @ 8.5 in. cts.
- Check Shear
- = 33.998 psi ≤ 109.5 psi = νc o.k.
- Reinforcement - Footing - Bottom Steel
- Design the flexural steel in the bottom of the footing to resist the largest moment that the heel pile could exert on the footing. The largest heel pile bearing force was in Case IV. The heel pile will cause a larger moment about the stem face than the toe pile (even though there are two toe piles for every one heel pile) because it has a much longer moment arm about the stem face.
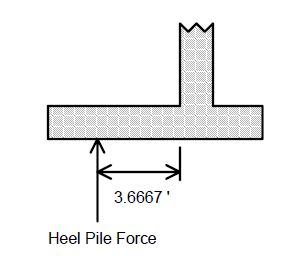
- Pile is embedded into footing 12 inches.
- b = 12 in.
- h = 36 in.
- d = 36 in. - 4 in. = 32 in.
- Apply Load Factors to Case IV Loads
- ΣV = 13.842 k/ft.
- ΣM = 41.735 (ft−k)/ft.
- e = = 3.015 ft.
- Moment arm = 3.015 ft. - 1.833 ft. = 1.182 ft.
- = 7.588 k/ft.
- = 27.825(ft−k)/ft.
- = 0.0301 ksi
- = 0.000505
- = 0.00196
- Use ρ = 4/3 ρ = 4/3 (0.000505) = 0.000673
- ASReq = ρbd = (0.000673)(12 in.)(32 in.) = 0.258 in2/ft.
- One #4 bar has As = 0.196 in2.
- s = 9.1 in.
- Use #4 bars @ 9 in. cts.
- Check Shear
- The critical section for shear for the toe is at a distance d = 21.75 inches from the face of the stem. The toe pile is 6 inches from the stem face so the toe pile shear does not affect the shear at the critical section. The critical section for shear is at the stem face for the heel so all of the force of the heel pile affects the shear at the critical section. The worst case for shear is Case IV.
- Vu = 7.588k
- = 23.248 psi ≤ 109.5 psi = νc o.k.
- Reinforcement - Shear Key
- b = 12 in.
- h = 12 in.
- cover = 3 in.
- d = 12 in. - 3 in. - 0.5(0.5 in.) = 8.75 in.
- Apply Load Factors
- PP = γβE (3.845k) = (1.3)(1.3)(3.845k) = 6.498k
- Mu = (0.912 ft.)(6.498k) = 5.926(ft−k)
- = 0.0860 ksi
- = 0.00146
- = 0.00292
- Use ρ = 4/3 ρ = 4/3(0.00146) = 0.00195
- ASReq = ρbd = (0.00195)(12 in.)(8.75 in.) = 0.205 in.2/ft.
- One #4 bar has As = 0.196 in2
- s = 11.5 in.
- Use #4 bars @ 11 in. cts.
- Check Shear
- = 72.807 psi < 109.5 psi = νc
- Reinforcement Summary
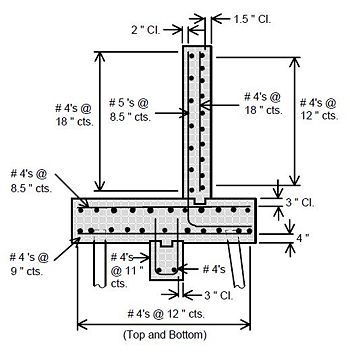
751.40.8.15.8 Dimensions
Cantilever Walls
Each section of wall shall be in increments of 4 ft. with a maximum length of 28'-0".
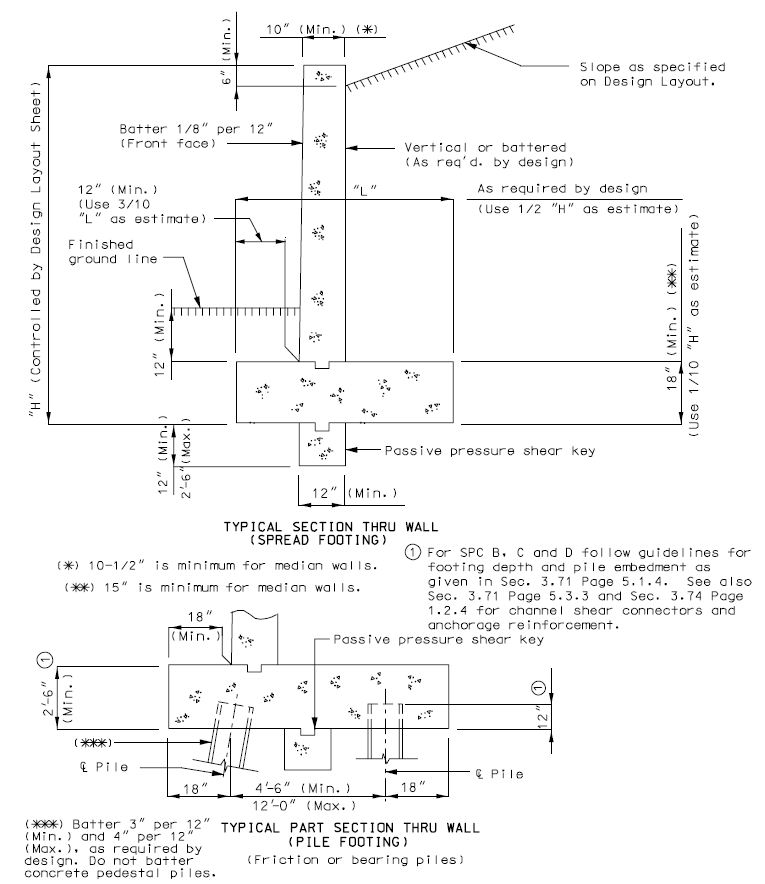
Each section of wall shall be in increments of 4 ft. with a maximum length of 28'-0".
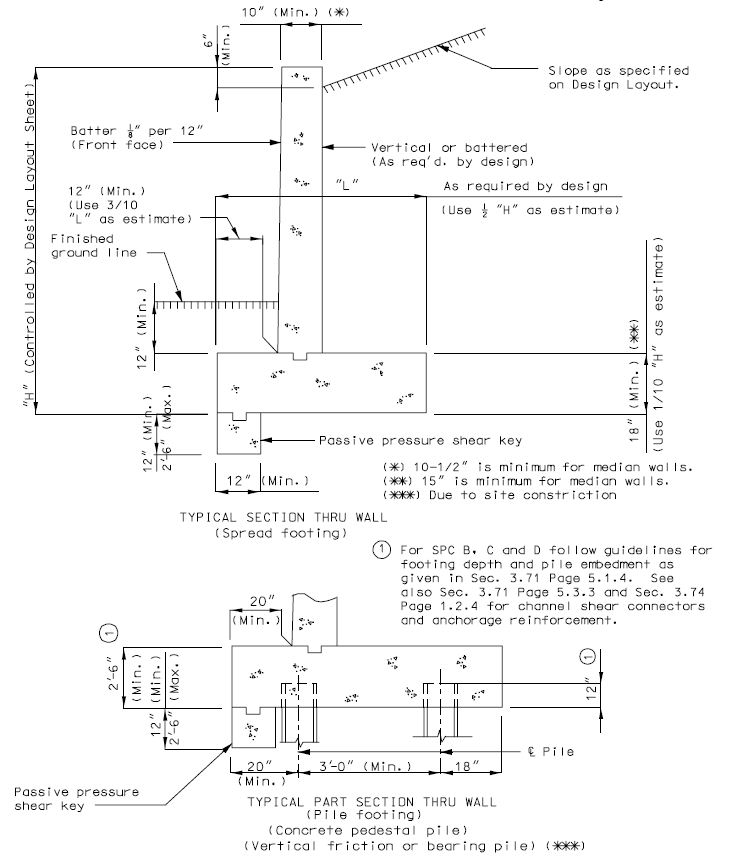
Cantilever Walls - L-Shaped
Each section of wall shall be in increments of 4 ft. with a maximum length of 28'-0".
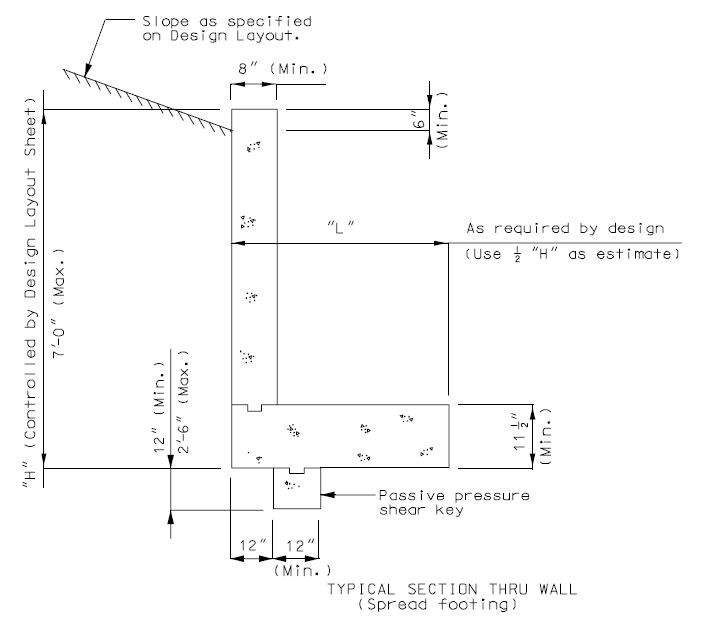
Counterfort Walls
| Notes: |
| Dimension "A" |
| • Maximum length = 28'-0". |
| • Each section to be in 4'-0" increments. |
| • (See rustication recess details.) |
| Dimensions "B" & "C" |
| • As required by the design to balance the negative and positive moments. (See the design assumptions). |
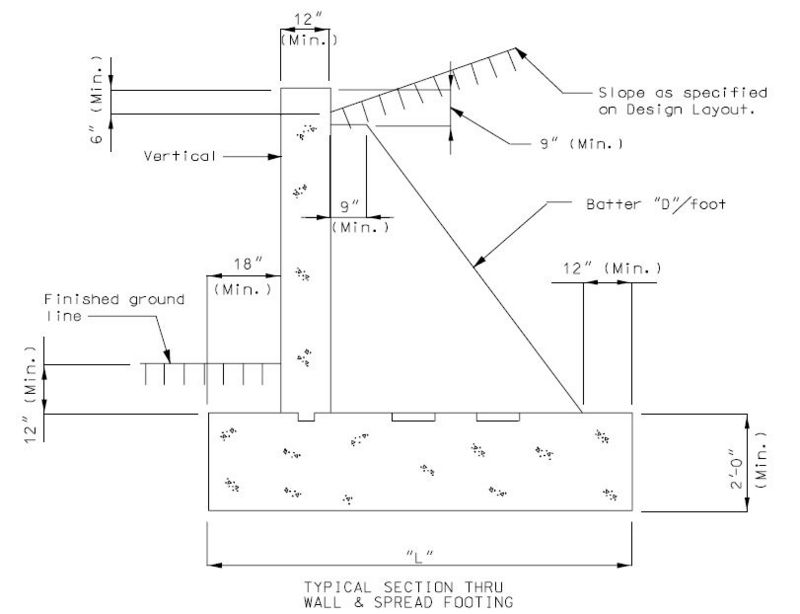
| Notes: |
| Batter "D": |
| * As required to maintain 9" minimum at the top of the counterfort and 12" minimum edge distance at the top of the footing, between counterfort and footing edge. |
| * Batter to be given an eighth of an inch per foot of counterfort height. |
| Dimension "L": |
| * As required for stability. |
| * As an estimate, use "L" equal to 1/2 the height of "H". |
Sign-Board Type Counterfort Walls
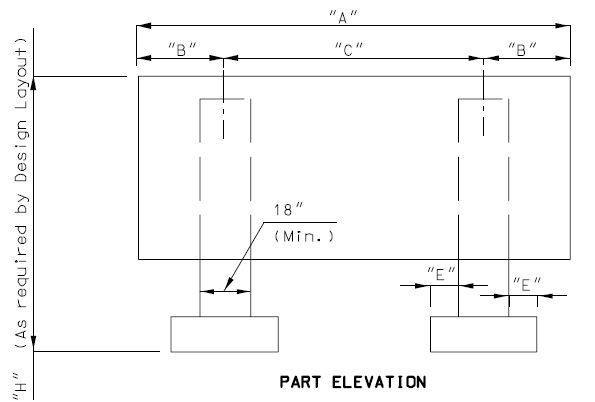
| Notes: |
| Dimension "A" |
| * Maximum length = 28'-0". |
| * Each section to be in 4'-0" increments. |
| * (See rustication recess details.) |
| Dimensions "B" & "C" |
| * As required by the design to balance the negative and positive moments. (See the design assumptions). |
| Dimension "E" |
| * (Sign-board type only) |
| * As required to maintain footing pressure within the allowable for existing foundation material. 12" minimum. |
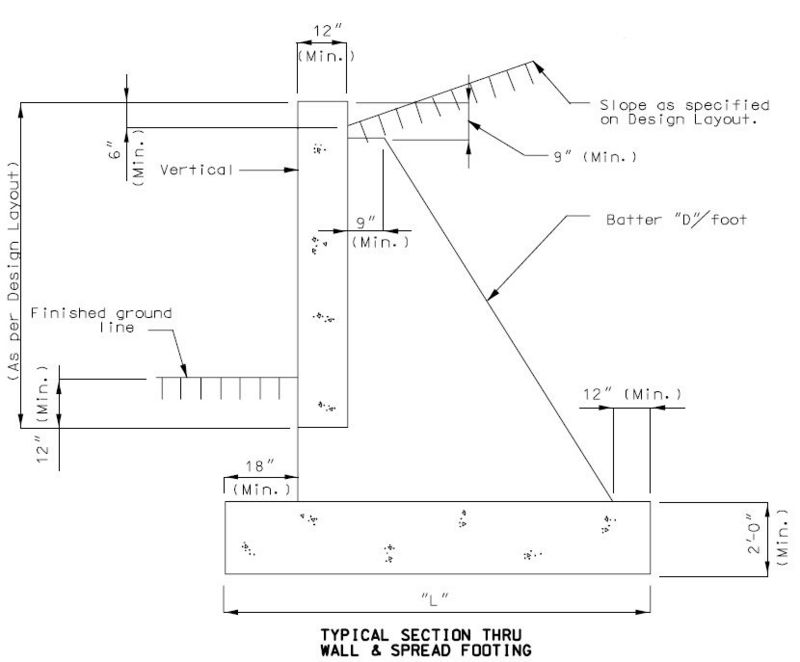
| Notes: |
| Batter "D": |
| * As required to maintain 9" minimum at the top of the counterfort and 12" minimum edge distance at the top of the footing, between counterfort and footing edge. |
| * Batter to be given an eighth of an inch per foot of counterfort height. |
| Dimension "L": |
| * As required for stability. |
| * As an estimate, use "L" equal to 1/2 the height of "H". |
751.40.8.15.9 Reinforcement
Cantilever Walls
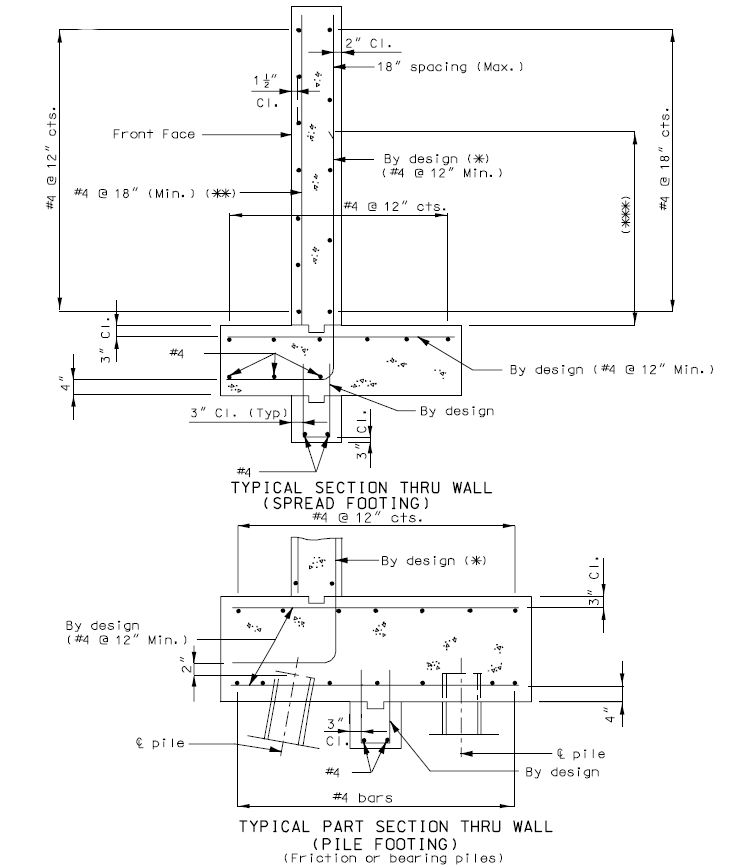
| (*) Alternate long and short bars at equal spaces. |
| (**) If collision forces are assumed, use #4 @ 12" cts. min. and extend at least development length into footing. (See EPG 751.5.9.2.8.1 Development and Lap Splice General.) |
| (***) Theo. cut-off for bending + development length. (Wall height over 10' only.) |
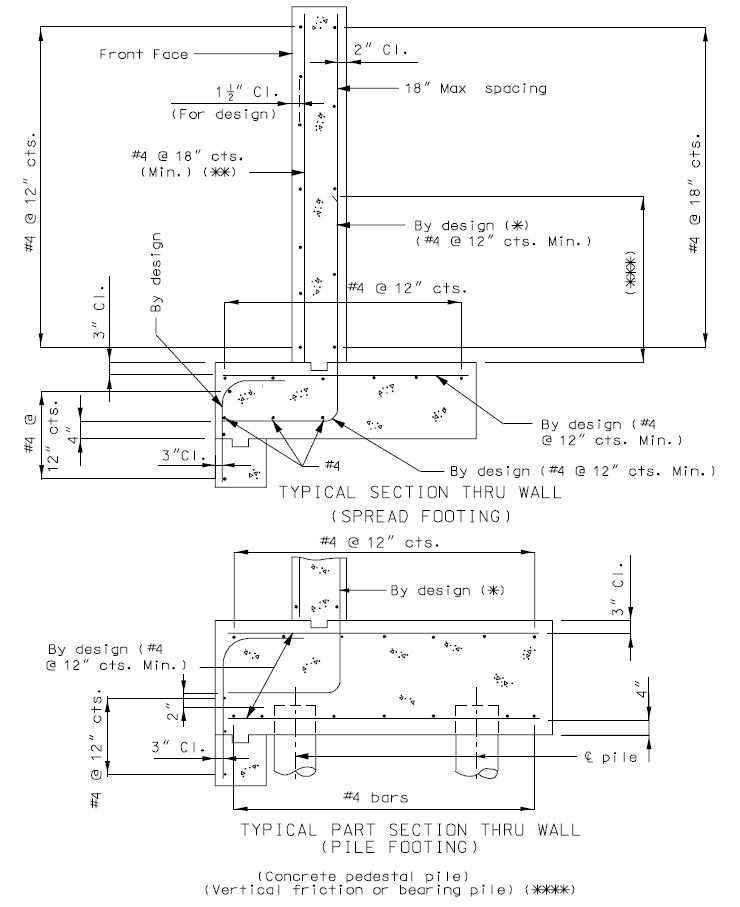
| (*) Alternate long and short bars at equal spaces. |
| (**) If collision forces are assumed, use #4 @ 12" cts. min. and extend at least development length into footing. (See EPG 751.5.9.2.8.1 Development and Lap Splice General.) |
| (***) Theo. cut-off for bending + development length. (Wall height over 10' only.) |
| (****) Due to site constriction. |
Cantilever Walls - L-Shaped
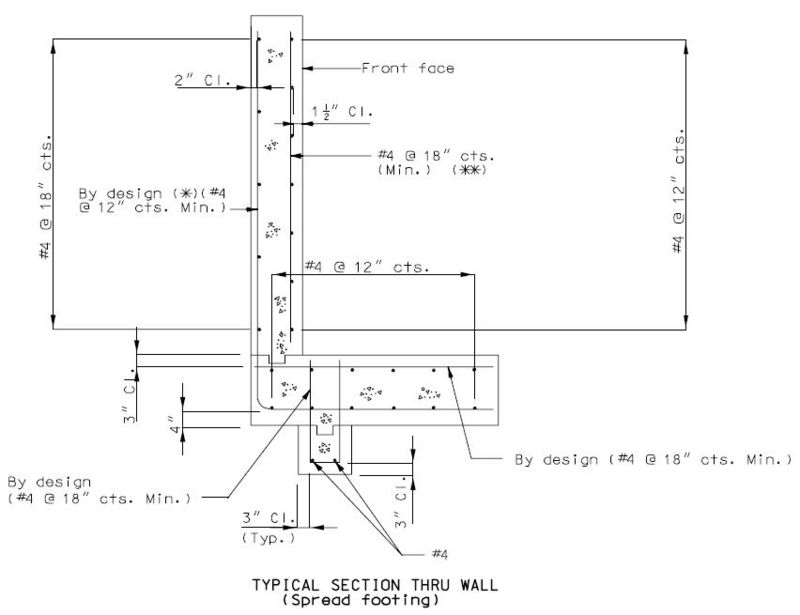
| (*) Do not splice stress bars in the fill face at top of footing. |
| (**) If collision forces are assumed, use #4 @ 12" cts. min. and extend at least development length into footing. (See EPG 751.5.9.2.8.1 Development and Lap Splice General.) |
Counterfort Walls
- Wall and Stem
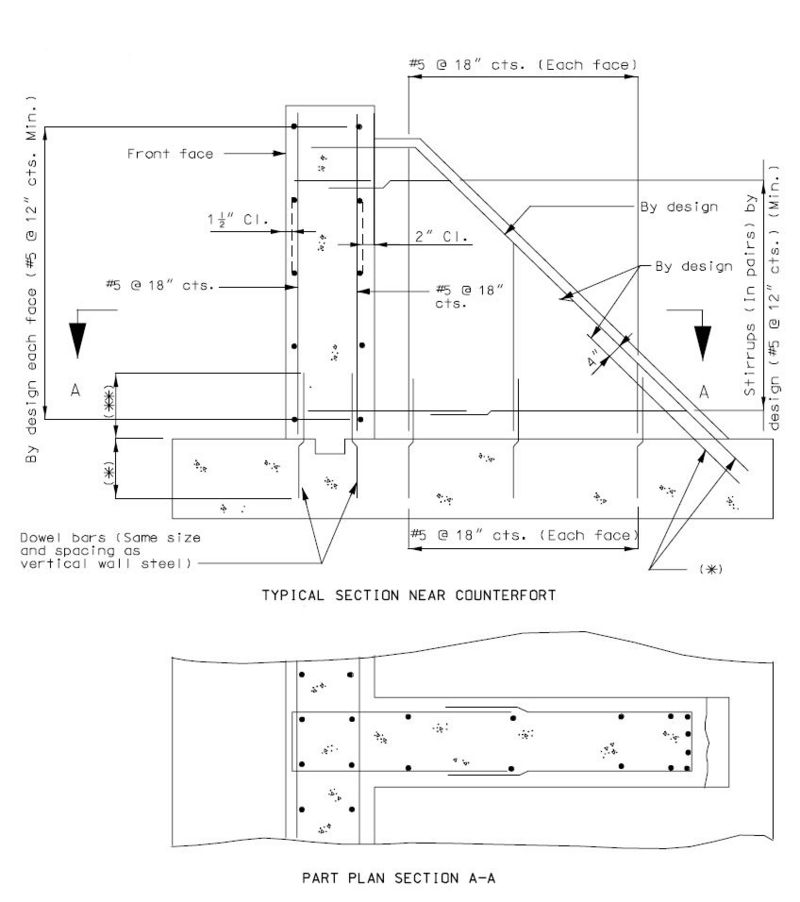
| (*) Use development length or standard hook in accordance with EPG 751.5.9.2.8.1 Development and Lap Splice General. |
| (**) See lap splices Class B. (See EPG 751.5.9.2.8.1 Development and Lap Splice General.) |
- Footing
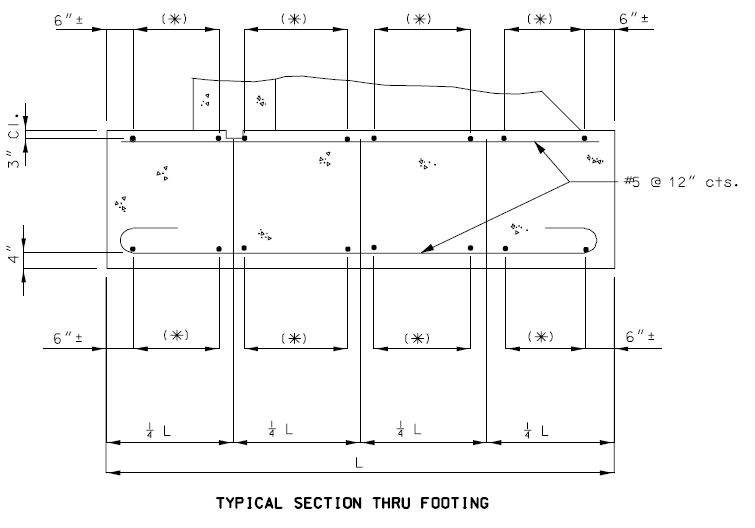
| (*) By design for loads and footing pressures on section under consideration. (#5 @ 12" cts. is the minimum.) |
Counterfort Walls - Sign-Board Type
- Wall and Stem
- Refer to "Counterfort Walls, Wall and Stem", above.
- Spread Footing
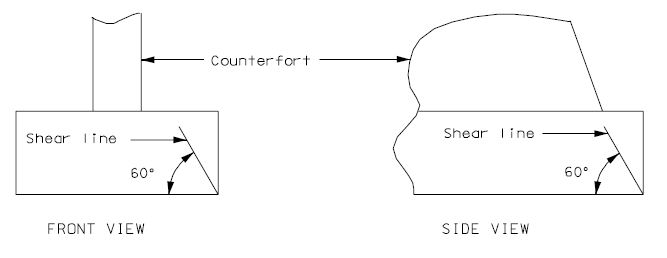
- If the shear line is within the counterfort projected (longitudinally or transversely), the footing may be considered satisfactory for all conditions. If outside of the counterfort projected, the footing must be analyzed and reinforced for bending and checked for bond stress and for diagonal tension stress.
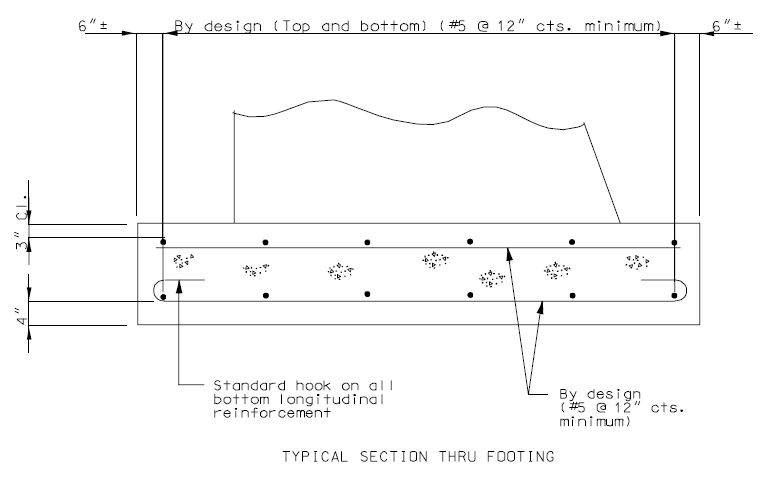
751.40.8.15.10 Details
Non-Keyed Joints
Each section of wall shall be in increments of 4 ft. with a maximum length of 28'-0".
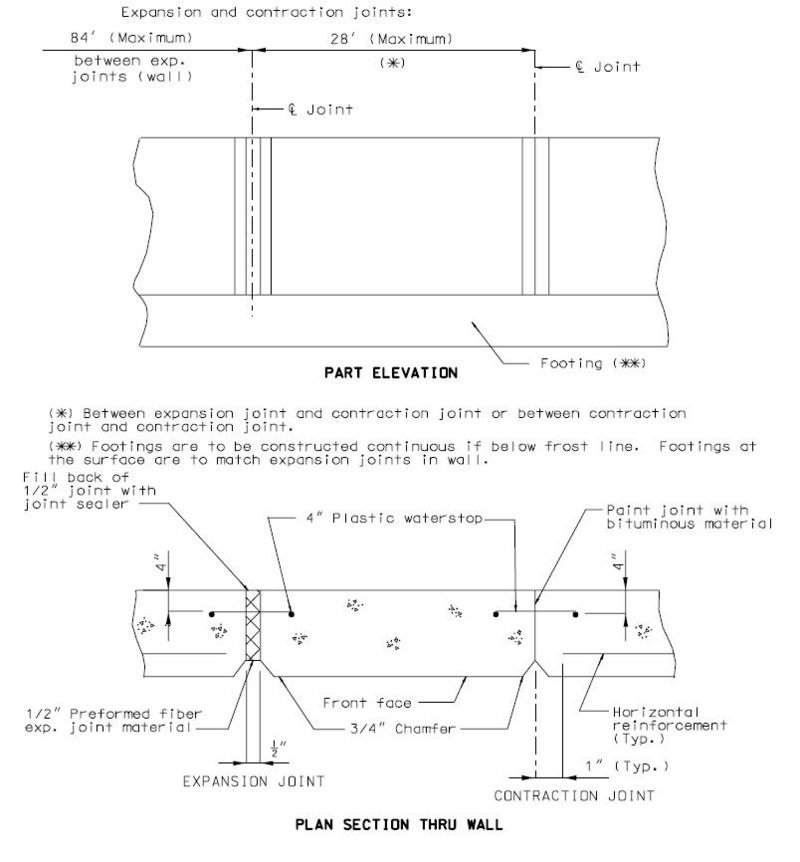
Keyed Joints
Rustication Recess
Drains
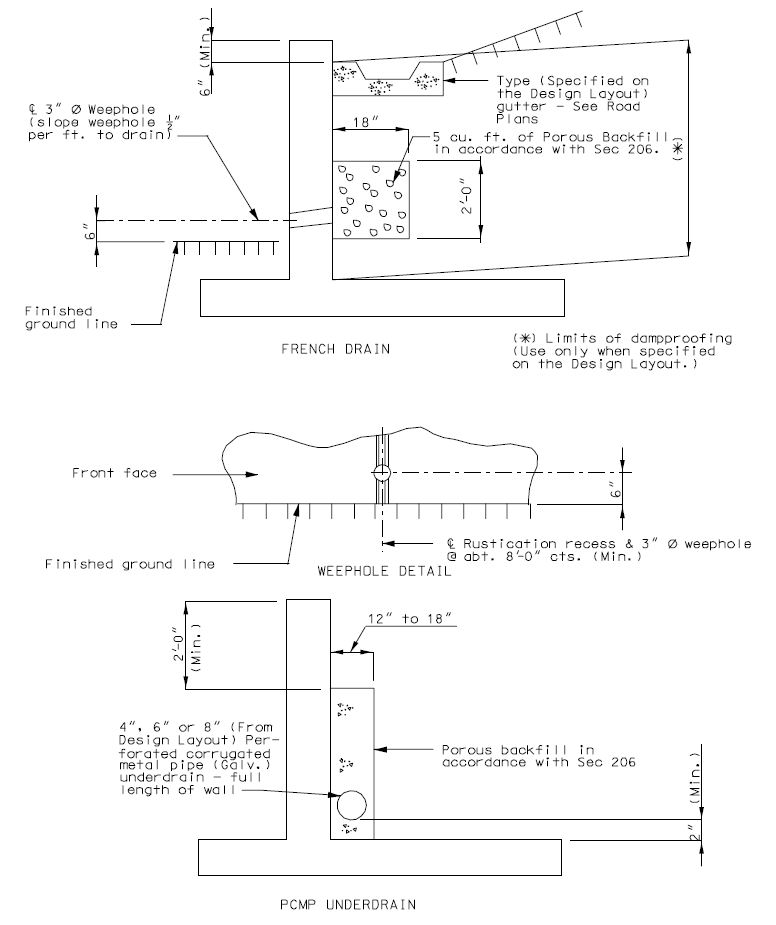
Construction Joint Keys:
- Cantilever Walls
- Counterfort Walls
- Key length: Divide the length "A" into an odd number of spaces of equal lengths. Each space shall not exceed a length of 24 inches. Use as few spaces as possible with the minimum number of spaces equal to three (or one key).
- Key width = Counterfort width/3 (to the nearest inch)
- Key depth = 2" (nominal)
- Sign-Board Walls
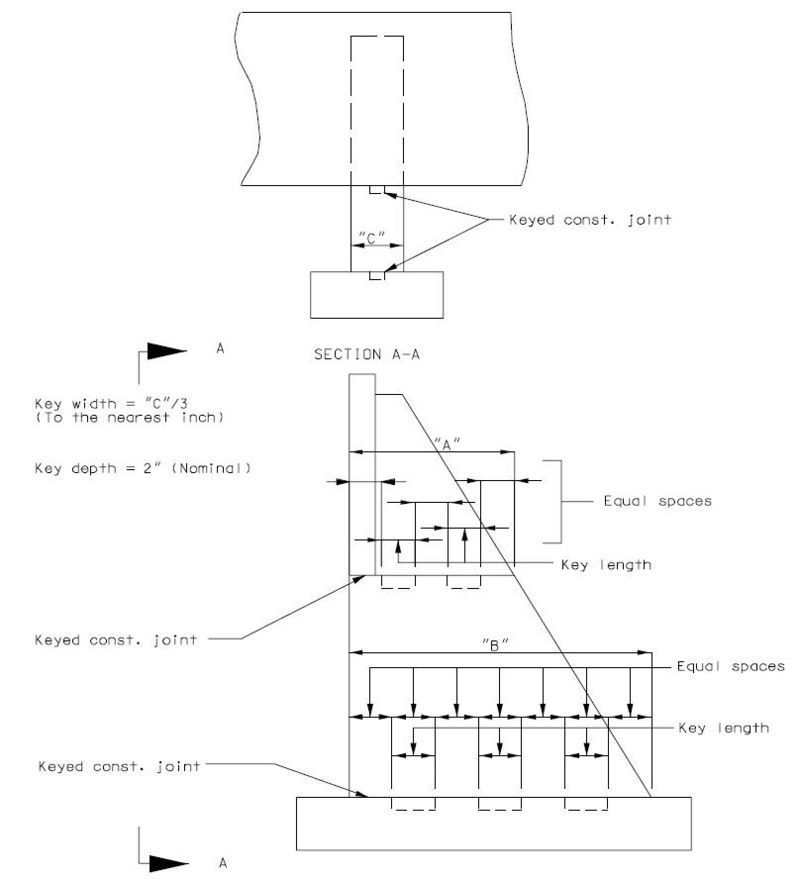
- Key length = divide length "A" or "B" into an odd number of spaces of equal lengths. Each space length shall not exceed 24 inches. Use as few spaces as possible with the minimum number of spaces equal to three (or one key).