Difference between revisions of "321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation"
(Part of EPG 321 general re-write. FHWA mandates that all bridges and foundations be designed in accordance with LRFD Bridge Design specs.) |
m (removed errant symbol) |
||
| (11 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Methods provided for [[751.37 Drilled Shafts|design of drilled shafts]], [[751.38 Spread Footings|design of spread footings]] and [[321.1 Design of Earth Slopes|design of earth slopes]] require that both values | + | Methods provided for [[751.37 Drilled Shafts|design of drilled shafts]], [[751.38 Spread Footings|design of spread footings]] and [[321.1 Design of Earth Slopes|design of earth slopes]] require that both values for design parameters and values for coefficients of variation for the design parameters be established. The provisions of this article provide procedures for establishing design parameter values and design parameter uncertainty for use with these provisions. |
==321.3.1 General == | ==321.3.1 General == | ||
{|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
|- | |- | ||
| − | |align="center"|'''[[#321.3. | + | |align="center"|'''[[#321.3.9 Commentary|Commentary for EPG 321.3.1 General''']] |
|} | |} | ||
| − | Provisions of [[751.37 Drilled Shafts|EPG 751.37]], [[751.38 Spread Footings|EPG 751.38]] and [[321.1 Design of Earth Slopes|EPG 321.1]] were developed presuming that the design parameter values used for the provisions are mean values of the relevant parameters. These EPG provisions also require that the coefficients of variation for the design parameters be established to reflect the variability and uncertainty present in the design parameters. Methods for establishing both mean values and coefficients of variation for design parameters for relevant strata are provided in these provisions. | + | Provisions of [[751.37 Drilled Shafts|EPG 751.37 Drilled Shafts]], [[751.38 Spread Footings|EPG 751.38 Spread Footings]] and [[321.1 Design of Earth Slopes|EPG 321.1 Design of Earth Slopes]] were developed presuming that the design parameter values used for the provisions are mean values of the relevant parameters. These EPG provisions also require that the coefficients of variation for the design parameters be established to reflect the variability and uncertainty present in the design parameters. Methods for establishing both mean values and coefficients of variation for design parameters for relevant strata are provided in these provisions. |
===321.3.1.1 Relevant Design Parameters === | ===321.3.1.1 Relevant Design Parameters === | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.1.1 Relevant Design Parameters|Commentary for EPG 321.3.1.1 Relevant Design Parameters ''']] | ||
| + | |} | ||
| + | |||
| + | Design parameters that require estimation of mean values and values for the coefficient of variation in EPG 751.37, EPG 751.38 and EPG 321.1 include those shown in Table 321.3.1.1 | ||
| + | |||
| − | + | <center>'''Table 321.3.1.1, Summary of Design Parameters that Require Estimation of Mean Values and Values of Coefficient of Variation''' | |
| − | + | ||
| + | {| border="1" class="wikitable" style="margin: 1em auto 1em auto" style="text-align:center" | ||
| + | |+ | ||
| + | ! style="background:#BEBEBE" colspan="2"|Design Parameter!! style="background:#BEBEBE" rowspan="2" width="300"|Relevant EPG Article(s) | ||
| + | |- | ||
| + | ! style="background:#BEBEBE" |Nomenclature !! style="background:#BEBEBE" |Description | ||
| + | |- | ||
| + | |''q<sub>u</sub>''||uniaxial compressive strength of rock|| [[751.37 Drilled Shafts#751.37.3.1 Axial Resistance for Individual Drilled Shafts in Rock (qu ≥ 100 ksf)|751.37.3.1]], [[751.37 Drilled Shafts#751.37.3.2 Axial Resistance for Individual Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)|751.37.3.2]]<br>[[751.37 Drilled Shafts#751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method|751.37.4.1]], [[751.37 Drilled Shafts#751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method|751.37.4.2]]<br>[[751.38 Spread Footings#751.38.3.1 Bearing Resistance for Spread Footings on Rock (qu ≥ 100 ksf)|751.38.3.1]], [[751.38 Spread Footings#751.38.3.2 Bearing Resistance for Spread Footings on Weak Rock (5 ksf ≤ qu ≤ 100 ksf)|751.38.3.2]]<br>[[751.38 Spread Footings#751.38.4.1 Settlement of Spread Footings on Rock (qu ≥ 100 ksf)|751.38.4.1]], [[751.38 Spread Footings#751.38.4.2 Settlement of Spread Footings on Weak Rock (5 ksf ≤ qu ≤ 100 ksf)|751.38.4.2]] | ||
| + | |- | ||
| + | |''s<sub>u</sub>''||undrained shear strength|| [[321.1 Design of Earth Slopes#Accordingly, a load factor of 1.0|321.1.2.4]], [[751.37 Drilled Shafts#751.37.3.6 Axial Resistance for Individual Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)|751.37.3.6]]<br>[[751.37 Drilled Shafts#751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method|751.37.4.1]], [[751.37 Drilled Shafts#751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method|751.37.4.2]]<br>[[751.38 Spread Footings#751.38.3.3 Bearing Resistance for Spread Footings on Cohesive Soils (su ≤ 5,000 psf)|751.38.3.3]] | ||
| + | |- | ||
| + | |''c''|| total stress cohesion intercept|| [[321.1 Design of Earth Slopes#Accordingly, a load factor of 1.0|321.1.2.4]] | ||
| + | |- | ||
| + | |''tan ϕ''|| tangent of total stress friction angle|| [[321.1 Design of Earth Slopes#Accordingly, a load factor of 1.0|321.1.2.4]] | ||
| + | |- | ||
| + | |<math>\overline c </math>|| effective stress cohesion intercept|| [[321.1 Design of Earth Slopes#321.1.2.5 Resistance factors for long-term, fully drained conditions|321.1.2.5]] | ||
| + | |- | ||
| + | |''tan'' <math>\overline \phi </math>|| tangent of effective stress friction angle|| [[321.1 Design of Earth Slopes#321.1.2.5 Resistance factors for long-term, fully drained conditions|321.1.2.5]] | ||
| + | |- | ||
| + | |''c<sub>c</sub>''||compression index|| [[321.1 Design of Earth Slopes#321.1.3.2 Settlement Due to Compression of Foundation Soils|321.1.3.2]], [[751.38 Spread Footings#751.38.4.3 Settlement of Spread Footings on Cohesive Soils|751.38.4.3]] | ||
| + | |- | ||
| + | |''c<sub>r</sub>''|| recompression index|| [[321.1 Design of Earth Slopes#321.1.3.2 Settlement Due to Compression of Foundation Soils|321.1.3.2]], [[751.38 Spread Footings#751.38.4.3 Settlement of Spread Footings on Cohesive Soils|751.38.4.3]] | ||
| + | |- | ||
| + | |''σ'<sub>p</sub>''|| pre-consolidation stress|| [[321.1 Design of Earth Slopes#321.1.3.2 Settlement Due to Compression of Foundation Soils|321.1.3.2]], [[751.38 Spread Footings#751.38.4.3 Settlement of Spread Footings on Cohesive Soils|751.38.4.3]] | ||
| + | |- | ||
| + | |''N<sub>eq</sub>''|| equivalent SPT ''N''-value|| [[751.37 Drilled Shafts#751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)|751.37.3.3]], [[751.37 Drilled Shafts#751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method|751.37.4.1]]<br>[[751.37 Drilled Shafts#751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method|751.37.4.2]] | ||
| + | |- | ||
| + | |''TCP''||penetration from Texas Cone Penetration test||[[751.37 Drilled Shafts#751.37.3.4 Axial Resistance for Individual Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)|751.37.3.4]], [[751.37 Drilled Shafts#751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method|751.37.4.1]]<br>[[751.37 Drilled Shafts#751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method|751.37.4.2]] | ||
| + | |- | ||
| + | |''I<sub>s(50)</sub>''|| corrected point load index|| [[751.37 Drilled Shafts#751.37.3.5 Axial Resistance for Individual Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)|751.37.3.5]], [[751.37 Drilled Shafts#751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method|751.37.4.1]]<br>[[751.37 Drilled Shafts#751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method|751.37.4.2]] | ||
| + | |} | ||
| + | </center> | ||
===321.3.1.2 Development of Design Profiles for Relevant Design Properties === | ===321.3.1.2 Development of Design Profiles for Relevant Design Properties === | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.1.2 Development of Design Profiles for Relevant Design Properties |Commentary for EPG 321.3.1.2 Development of Design Profiles for Relevant Design Properties ''']] | ||
| + | |} | ||
| − | The provisions of this article are intended to produce rational “design profiles” of properties needed for application of EPG 751.37, EPG 751.38 and EPG 321.1. These design profiles establish a model for how a parameter varies with depth or elevation, as well as the variability | + | The provisions of this article are intended to produce rational “design profiles” of properties needed for application of [[751.37 Drilled Shafts|EPG 751.37 Drilled Shafts]], [[751.38 Spread Footings|EPG 751.38 Spread Footings]] and [[321.1 Design of Earth Slopes|EPG 321.1 Design of Earth Slopes]]. These design profiles establish a model for how a parameter varies with depth or elevation, as well as the variability or uncertainty associated with the model. |
| − | For the purposes of this provision, design profiles are assumed to be composed of a number of individual strata. The | + | For the purposes of this provision, design profiles are assumed to be composed of a number of individual strata. The design parameter within an individual stratum is assumed to have values that are either constant, or linearly varying with depth or elevation as illustrated in Fig. 321.3.1.1. All design profiles can be reasonably represented as some combination of strata that have either a constant property or linearly varying property within each stratum. Regardless of whether the parameter value is assumed to be constant or linearly varying with depth, the variability or uncertainty in the parameter value within a single stratum is assumed to be constant, and represented by a constant value of the coefficient of variation (''COV''). |
| − | + | [[image:321.3.1.1.jpg|center|750px|thumb|'''<center>Fig. 321.3.1.1, Example design profile for uniaxial compressive strength showing interpretation of different strata and resulting parameter model including coefficients of variation. '''</center>]] | |
===321.3.1.3 Minimum Testing Requirements === | ===321.3.1.3 Minimum Testing Requirements === | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.1.3 Minimum Testing Requirements |Commentary for EPG 321.3.1.3 Minimum Testing Requirements ''']] | ||
| + | |} | ||
| − | Method provided in this article and EPG 751.37, EPG 751.38 and EPG 321.1 were developed to accurately account for variability and uncertainty associated with geotechnical design parameters regardless of the quantity of testing performed. However, the methods provided in this article require | + | Method provided in this article and EPG 751.37, EPG 751.38 and EPG 321.1 were developed to accurately account for variability and uncertainty associated with geotechnical design parameters regardless of the quantity of testing performed. However, the methods provided in this article require a minimum of three measurements within each stratum for application of the methods. For cases where fewer than three measurements are available for a particular stratum, designers must resort to use of judgment for estimation of the coefficient of variation as described in the commentary to these guidelines. |
| − | |||
| − | |||
==321.3.2 Design Values for Strata with Constant Properties == | ==321.3.2 Design Values for Strata with Constant Properties == | ||
{|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
|- | |- | ||
| − | |align="center"|'''[[#321.3 | + | |align="center"|'''[[#Commentary on EPG 321.3.2 Design Values for Strata with Constant Properties |Commentary for EPG 321.3.2 Design Values for Strata with Constant Properties ''']] |
|} | |} | ||
| − | The provisions of this article shall be satisfied when the | + | The provisions of this article shall be satisfied when the parameter of interest is deemed to be constant over the stratum of interest. |
===321.3.2.1 Establishing Mean Values for Strata with Constant Property === | ===321.3.2.1 Establishing Mean Values for Strata with Constant Property === | ||
| − | Design values for parameters in strata that are judged to have practically constant or uniform values for the | + | Design values for parameters in strata that are judged to have practically constant or uniform values for the parameter of interest shall be established as the arithmetic mean of the available measurements: |
{| style="margin: 1em auto 1em auto" width="800" | {| style="margin: 1em auto 1em auto" width="800" | ||
|- | |- | ||
| − | |align="left"|<math> y = \overline y = \frac{\sum_{i=1}^n \hat y_i}{n}</math>||align="center"| (consistent units | + | |align="left"|<math> y = \overline y = \frac{\sum_{i=1}^n \hat y_i}{n}</math>||align="center"| (consistent units)||align="right"|Equation 321.3.2.1 |
|} | |} | ||
| Line 54: | Line 98: | ||
:''n'' = number of available measurements used to establish the mean value (dimensionless). | :''n'' = number of available measurements used to establish the mean value (dimensionless). | ||
| − | The mean value | + | The mean value of the relevant parameter can be calculated from all measured values using the AVERAGE function in Microsoft Excel<sup>©</sup> or similar functions in other computer programs. |
===321.3.2.2 Establishing COV Values for Strata with Constant Property === | ===321.3.2.2 Establishing COV Values for Strata with Constant Property === | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|[[321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation#Commentary on EPG 321.3.2.2|'''Commentary on EPG 321.3.2.2 Establishing COV Values for Strata with Constant Property''']] | ||
| + | |} | ||
| + | |||
The coefficient of variation of the mean value for the design parameter shall be established from the set of available measurements as: | The coefficient of variation of the mean value for the design parameter shall be established from the set of available measurements as: | ||
{| style="margin: 1em auto 1em auto" width="800" | {| style="margin: 1em auto 1em auto" width="800" | ||
|- | |- | ||
| − | |align="left"|<math>COV_y = \frac{\ | + | |align="left"|<math>COV_y = \frac{\zeta \sigma_y}{y} = \frac{\zeta \frac{\sigma_\hat y}{\sqrt n}}{y}</math>||align="center"| (dimensionless)||align="right"|Equation 321.3.2.2 |
|} | |} | ||
| Line 70: | Line 119: | ||
:<math>\sigma_y = \frac{\sigma_\hat y}{\sqrt n}</math> = standard deviation of the mean value of parameter of interest (consistent units), | :<math>\sigma_y = \frac{\sigma_\hat y}{\sqrt n}</math> = standard deviation of the mean value of parameter of interest (consistent units), | ||
| − | :<math>\bold \ | + | :<math>\bold \zeta</math> = empirical modifier to account for effects of quantity of tests (dimensionless), |
:''y'' = design, or “model” value for parameter of interest (consistent units), | :''y'' = design, or “model” value for parameter of interest (consistent units), | ||
| − | :<math>\sigma_\hat y = \sqrt{\frac{\sum_{i=1}^n (\hat | + | :<math>\sigma_\hat y = \sqrt{\frac{\sum_{i=1}^n (\hat y_i - \overline y)^2}{n-1}}</math> = standard deviation of measurements of parameter of interest (consistent units), |
:''n'' = number of available measurements used to establish the mean value (dimensionless) and | :''n'' = number of available measurements used to establish the mean value (dimensionless) and | ||
| − | :<math>\hat y</math> = measured value of a parameter (consistent units). | + | :<math>\hat y</math> = measured value of a parameter of interest (consistent units). |
| − | The standard deviation of the measurements, <math>\sigma_\hat y</math>, can be calculated from the equation provided | + | The standard deviation of the measurements, <math>\sigma_\hat y</math>, can be calculated from the equation provided using the STDEV function in Microsoft Excel<sup>©</sup> or similar functions in other computer programs. The empirical parameter <math>\bold \zeta</math> shall be determined as provided in [[#321.3.5 Uncertainty Modifiers to Account for Quantity of Tests|EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests]]. |
==321.3.3 Design Values for Strata with Linearly Varying Properties == | ==321.3.3 Design Values for Strata with Linearly Varying Properties == | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.3 Design Values for Strata with Linearly Varying Properties |Commentary for EPG 321.3.3 Design Values for Strata with Linearly Varying Properties ''']] | ||
| + | |} | ||
| + | |||
The provisions of this article shall be satisfied when the property of interest is deemed to vary linearly with depth or elevation over the stratum of interest. | The provisions of this article shall be satisfied when the property of interest is deemed to vary linearly with depth or elevation over the stratum of interest. | ||
===321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property === | ===321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property === | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property |Commentary for EPG 321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property ''']] | ||
| + | |} | ||
| + | |||
Design values for parameters in strata where the property of interest is judged to vary linearly with depth or elevation shall be established from a linear best fit relation to the available measurements: | Design values for parameters in strata where the property of interest is judged to vary linearly with depth or elevation shall be established from a linear best fit relation to the available measurements: | ||
{| style="margin: 1em auto 1em auto" width="800" | {| style="margin: 1em auto 1em auto" width="800" | ||
|- | |- | ||
| − | |align="left"|''y = b + mz'' ||align="center"| (consistent units | + | |align="left"|''y = b + mz'' ||align="center"| (consistent units)||align="right"|Equation 321.3.3.1 |
|} | |} | ||
| Line 103: | Line 162: | ||
:''m'' = slope from linear least squares fit to the available data (consistent units). | :''m'' = slope from linear least squares fit to the available data (consistent units). | ||
| − | The coefficients ''m'' and ''b'' can be determined using the LINEST function in Microsoft | + | The coefficients ''m'' and ''b'' can be determined using the LINEST function in Microsoft Excel<sup>©</sup> or similar functions in other computer programs. |
===321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property === | ===321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property === | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property |Commentary for EPG 321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property ''']] | ||
| + | |} | ||
The coefficient of variation of the mean value for the design parameter shall be established from the set of available measurements as: | The coefficient of variation of the mean value for the design parameter shall be established from the set of available measurements as: | ||
| Line 111: | Line 174: | ||
{| style="margin: 1em auto 1em auto" width="800" | {| style="margin: 1em auto 1em auto" width="800" | ||
|- | |- | ||
| − | |align="left"|<math>COV_y = \frac{\ | + | |align="left"|<math>COV_y = \frac{\zeta \sigma_y}{y} = \frac {\zeta \sqrt{z^2 \sigma_m^2 + \sigma_b^2 + 2z\rho\sigma_b\sigma_m}}{y}</math> ||align="center"| (dimensionless)||align="right"|Equation 321.3.3.2 |
|} | |} | ||
| Line 118: | Line 181: | ||
:''COV<sub>y</sub>'' = coefficient of variation for mean value of design parameter of interest (dimensionless), | :''COV<sub>y</sub>'' = coefficient of variation for mean value of design parameter of interest (dimensionless), | ||
:<math>\sigma_y = \sqrt{z^2 \sigma_m^2 + \sigma_b^2 + 2z\rho\sigma_b\sigma_m}</math> = standard deviation of the mean value of parameter of interest (consistent units), | :<math>\sigma_y = \sqrt{z^2 \sigma_m^2 + \sigma_b^2 + 2z\rho\sigma_b\sigma_m}</math> = standard deviation of the mean value of parameter of interest (consistent units), | ||
| − | :<math>\bold \ | + | :<math>\bold \zeta</math> = empirical modifier to account for effects of quantity of tests (dimensionless), |
| − | :''y'' = mean value of parameter from the set of measurements (consistent units), | + | :''y'' = ''b'' + ''mz'' = mean value of parameter from the set of measurements (consistent units), |
:''z'' = depth or elevation (consistent units of length), | :''z'' = depth or elevation (consistent units of length), | ||
:''σ<sub>m</sub>'' = standard error in the slope, ''m'', of the least squares fit (consistent units), | :''σ<sub>m</sub>'' = standard error in the slope, ''m'', of the least squares fit (consistent units), | ||
| Line 125: | Line 188: | ||
:<math>\bold \rho</math> = correlation coefficient for ''m'' and ''b'' from the least squares fit (dimensionless). | :<math>\bold \rho</math> = correlation coefficient for ''m'' and ''b'' from the least squares fit (dimensionless). | ||
| − | The standard errors for the slope and intercept of the least squares fit (''σ<sub>m</sub>'' and ''σ<sub>b</sub>'') can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs. The empirical parameter <math>\bold \ | + | The standard errors for the slope and intercept of the least squares fit (''σ<sub>m</sub>'' and ''σ<sub>b</sub>'') can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs. The empirical parameter <math>\bold \zeta</math> shall be determined as provided in [[#321.3.5 Uncertainty Modifiers to Account for Quantity of Tests|EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests]]. The correlation coefficient 𝜌 can be determined using method described in the accompanying commentary document, or can conservatively be assumed to be equal to 1.0. |
| + | |||
| + | Since ''COV<sub>y</sub>'' from Equation 321.3.3.2 varies with depth or elevation, ''z'', a nominal average value for ''COV<sub>y</sub>'' shall be selected and used for design. This average value can be calculated as a rigorous average of value computed over the depth or elevation range for the stratum, or can be selected by judgment based on values computed over the depth or elevation range of the stratum. | ||
| + | |||
| + | ==321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters== | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters|Commentary for EPG 321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters''']] | ||
| + | |} | ||
| + | |||
| + | The provisions of this article shall be satisfied when establishing design values for Mohr-Coulomb shear strength parameters, ''c'' and ''ϕ''. This is the case for Mohr-Coulomb shear strength parameters established in terms of total stresses, i.e. ''c'' and ''ϕ'', or for Mohr-Coulomb shear strength parameters established in terms of effective stresses, i.e. <math>\overline c </math> and <math>\overline \phi </math>. In all cases such parameters will be presumed to be constant over a particular stratum; assigning linearly varying values of ''c'' and/or ''ϕ'' within a single stratum is not permitted. | ||
| + | |||
| + | ===321.3.4.1 Establishing Mean Values for c and ϕ in Terms of Total Stresses=== | ||
| + | |||
| + | Design values for ''c'' and ''ϕ'' for total stress analyses shall be established from a linear best fit relation to the available shear strength measurements made at different total confining stresses (e.g. from unconsolidated-undrained type triaxial tests). The best fit linear relation will be of the form: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"| ''s = c + σtanϕ'' ||align="center"| (consistent units)||align="right"|Equation 321.3.4.1 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''s'' = f(''σ'') = design, or “model” value for shear strength in terms of total stresses (consistent units of stress), | ||
| − | = | + | :''σ'' = total stress (consistent units of stress), |
| − | ''' | + | :''c'' = total stress “cohesion intercept” from linear least squares fit to the available data (consistent units of stress), and |
| + | |||
| + | :tan''ϕ'' = slope of failure envelope from linear least squares fit to the available data (dimensionless). | ||
| + | |||
| + | The coefficients ''c'' and tan''ϕ'' can be determined using the LINEST function in Microsoft Excel<sup>©</sup> or similar functions in other computer programs where the function is fit to data reflecting the shear stress and total normal stress on the failure plane at failure as described in the commentary to this article. | ||
| + | |||
| + | ===321.3.4.2 Establishing Mean Values for <math>\overline c </math> and <math>\overline \phi </math> in Terms of Effective Stresses=== | ||
| + | |||
| + | Design values for <math>\overline c </math> and <math>\overline \phi </math> for effective stress analyses shall be established from a linear best fit relation to the available shear strength measurements made at different effective confining stresses (e.g. from direct shear tests or from consolidated-drained or consolidated-undrained type triaxial tests). The best fit linear relation will be of the form: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"| ''s = <math>\overline c + \overline \sigma </math>tan<math>\overline \phi </math>'' ||align="center"| (consistent units)||align="right"|Equation 321.3.4.2 | ||
| + | |} | ||
| − | + | where | |
| − | + | :''s'' = f(<math>\overline \sigma </math>) = design, or “model” value for shear strength in terms of effective stresses (consistent units of stress), | |
| − | + | :<math>\overline \sigma </math> = effective stress (consistent units of stress), | |
| − | = | + | :<math>\overline c </math> = effective stress “cohesion intercept” from linear least squares fit to the available data (consistent units of stress), and |
| − | |||
| − | = | + | :tan<math>\overline \phi </math> = slope of failure envelope from linear least squares fit to the available data (dimensionless). |
| − | + | The coefficients <math>\overline c </math> and tan<math>\overline \phi </math> can be determined using the LINEST function in Microsoft Excel<sup>©</sup> or similar functions in other computer programs where the function is fit to data reflecting the shear stress and effective normal stress on the failure plane at failure as described in the commentary to this article. | |
| − | + | ===321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters=== | |
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters|Commentary for EPG 321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters''']] | ||
| + | |} | ||
| − | + | The coefficient of variation for the mean value of shear strength computed from Mohr-Coulomb shear strength parameters shall be established from the set of available measurements. If the measurements are in terms of total stresses, the coefficient of variation shall be calculated as: | |
| − | + | {| style="margin: 1em auto 1em auto" width="800" | |
| + | |- | ||
| + | |align="left"|<math>COV_{ss} = \frac{\zeta \sigma_{ss}}{s} = \frac {\zeta \sqrt{\sigma^2 \sigma_{tan \phi}^2 + \sigma_c^2 + 2 \sigma\rho\sigma_c\sigma_{tan \phi}}}{s}</math> ||align="center"| (dimensionless)||align="right"|Equation 321.3.4.3 | ||
| + | |} | ||
| − | + | where | |
| − | = | + | :''COV<sub>ss</sub>'' = coefficient of variation for mean value of shear strength (dimensionless), |
| − | + | :''σ<sub>ss</sub>'' = <math>\sqrt {\sigma^2 \sigma_{tan \phi}^2 + \sigma_c^2 + 2 \sigma\rho\sigma_c\sigma_{tan \phi}}</math> = standard deviation of the mean value of shear strength (consistent units of stress), | |
| − | = | + | :ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless), |
| − | == | + | :''s'' = ''c'' + ''σ'' tan''ϕ'' = mean value of shear strength from the set of measurements (consistent units of stress), |
| − | + | :''σ'' = total stress (consistent units of stress), | |
| − | = | + | :''σ<sub>tanϕ</sub>'' = standard error in the slope, tan''ϕ'', of the least squares fit (dimensionless), |
| − | These provisions are based on the assumption that the measurements are independent measurements (i.e. uncorrelated). While this assumption is seldom strictly satisfied, | + | :''σ<sub>c</sub>'' = standard error in the intercept, ''c'', of the least squares fit (consistent units), and |
| + | |||
| + | :''ρ'' = correlation coefficient for tan''ϕ'' and ''c'' from the least squares fit (dimensionless). | ||
| + | |||
| + | The standard errors for the slope and intercept of the least squares fit (''σ<sub>tanϕ</sub>'' and ''σ<sub>c</sub>'') can be determined using the LINEST function in Microsoft Excel<sup>©</sup> or similar functions in other computer programs. The empirical parameter ζ shall be determined as provided in [[#321.3.5 Uncertainty Modifiers to Account for Quantity of Tests|EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests]]. The correlation coefficient ''ρ'' can be determined using methods described in the accompanying commentary document, or can conservatively be assumed to be equal to 1.0. | ||
| + | |||
| + | If the measurements are in terms of effective stresses, the coefficient of variation shall be similarly calculated as: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math>COV_{ss} = \frac{\zeta \sigma_{ss}}{s} = \frac {\zeta \sqrt{\overline \sigma^2 \sigma_{tan \overline \phi}^2 + \sigma_{\overline c}^2 + 2 \overline \sigma\rho\sigma_{\overline c}\sigma_{tan \overline \phi}}}{s}</math> ||align="center"| (dimensionless)||align="right"|Equation 321.3.4.4 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''COV<sub>ss</sub>'' = coefficient of variation for mean value of shear strength (dimensionless), | ||
| + | |||
| + | :''σ<sub>ss</sub>'' = <math>\sqrt {\overline \sigma^2 \sigma_{tan \overline \phi}^2 + \sigma_{\overline c}^2 + 2 \overline \sigma\rho\sigma_{\overline c}\sigma_{tan \overline \phi}}</math> = standard deviation of the mean value of shear strength (consistent units of stress), | ||
| + | |||
| + | :ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless), | ||
| + | |||
| + | :''s'' = <math> \overline c + \overline \sigma tan \overline\phi</math> = mean value of shear strength from the set of measurements (consistent units of stress), | ||
| + | |||
| + | :<math>\overline \sigma</math> = effective stress (consistent units of stress), | ||
| + | |||
| + | :<math>\sigma_{tan \overline \phi}</math> = standard error in the slope, tan<math>\overline \phi</math>, of the least squares fit (dimensionless), | ||
| + | |||
| + | :<math>\sigma_{\overline c}</math> = standard error in the intercept, <math>\overline c</math>, of the least squares fit (consistent units), and | ||
| + | |||
| + | :''ρ'' = correlation coefficient for tan<math>\overline \phi</math> and <math>\overline c</math> from the least squares fit (dimensionless). | ||
| + | |||
| + | The standard errors for the slope and intercept of the least squares fit (<math>\sigma_{tan \overline \phi}</math> and <math>\sigma_{\overline c}</math>) can be determined using the LINEST function in Microsoft Excel<sup>©</sup> or similar functions in other computer programs. The empirical parameter ζ shall be determined as provided in [[#321.3.5 Uncertainty Modifiers to Account for Quantity of Tests|EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests]]. The correlation coefficient ''ρ'' can be determined using methods described in the accompanying commentary document, or can conservatively be assumed to be equal to 1.0. | ||
| + | |||
| + | Since ''COV<sub>ss</sub>'' from Equations 321.3.4.3 or 321.3.4.4 varies with the value of total stress, ''σ'', or effective stress, <math>\overline \sigma</math>, a nominal average value for ''COV<sub>ss</sub>'' shall be selected and used for design. This average value can be calculated as a rigorous average of value computed over the range of total stresses that are relevant for the particular design problem, or can be selected by judgment based on values computed over the appropriate range of normal stress. | ||
| + | |||
| + | ==321.3.5 Uncertainty Modifiers to Account for Quantity of Tests== | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests|Commentary for EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests''']] | ||
| + | |} | ||
| + | |||
| + | The empirical uncertainty modifier in Equations 321.3.2.2, 321.3.3.2, 321.3.4.3 and 321.3.4.4 shall be determined from Fig. 321.3.5.1 or calculated as | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math>\zeta = \frac{(n + 2.5)}{(n - 1)}</math> ||align="center"| (dimensionless)||align="right"|Equation 321.3.5.1 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless), and | ||
| + | |||
| + | :''n'' = number of available measurements (dimensionless). | ||
| + | |||
| + | [[image:321.3.5.1.jpg|center|750px|thumb|<center>'''Fig. 321.3.5.1, Uncertainty Modifier to account for number of measurements'''</center>]] | ||
| + | |||
| + | |||
| + | ==321.3.6 Design Values from Surrogate Measurements== | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.6 Design Values from Surrogate Measurements|Commentary for EPG 321.3.6 Design Values from Surrogate Measurements''']] | ||
| + | |} | ||
| + | |||
| + | The provisions of this article shall be satisfied when the parameter of interest is determined from “surrogate” measurements rather than from “direct” measurement of the parameter. The specific provisions to be satisfied depend on both the specific type of surrogate measurement and the specific design parameter of interest. | ||
| + | |||
| + | ===321.3.6.1 Establishing Mean Value of q<sub>u</sub> from Standard Penetration Tests in Shale=== | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.6.1 Establishing Mean Value of qu from Standard Penetration Tests in Shale|Commentary for EPG 321.3.6.1 Establishing Mean Value of q<sub>u</sub> from Standard Penetration Tests in Shale''']] | ||
| + | |} | ||
| + | |||
| + | Design values for the uniaxial compressive strength, ''q<sub>u</sub>'', of a specific shale stratum can be established from Standard Penetration Test (SPT) measurements in that stratum as: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math> q_u = e^{(1.354 \cdot \overline{ln (N_{eq})} - 3.587)}</math> ||align="center"| (ksf)||align="right"|Equation 321.3.6.1 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''q<sub>u</sub>'' = ''f''(<math> \overline{ln (N_{eq}})</math>) = design value for uniaxial compressive strength of shale (ksf), and | ||
| + | |||
| + | :<math> \overline{ln (N_{eq}})</math> = mean value of the natural log of ''N<sub>eq</sub>'' measurements in stratum of interest (consistent units). | ||
| + | |||
| + | Values for ''N<sub>eq</sub>'' shall be determined according to Equation Commentary 751.37.3.1 as described in [[751.37 Drilled Shafts#Commentary on EPG 751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)|EPG Commentary on 751.37.3.3]]. | ||
| + | |||
| + | ===321.3.6.2 Establishing COV Values for q<sub>u</sub> from Standard Penetration Tests in Shale=== | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.6.2 Establishing COV Values for qu from Standard Penetration Tests in Shale|Commentary for EPG 321.3.6.2 Establishing COV Values of q<sub>u</sub> from Standard Penetration Tests in Shale''']] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | The coefficient of variation of the design value for ''q<sub>u</sub>'' shall be established from the set of available ''N<sub>eq</sub>'' measurements within the stratum of interest as: | ||
| + | |||
| + | |||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math> COV_{q_u} = \frac{\zeta \sigma_{q_u}}{q_u} = \frac {\zeta \sqrt{{q_u}^2 \Bigg[1.654 + 1.882\frac{\sigma_{ln(\hat N_{eq})}^2}{n_s} - 0.503 \cdot \overline{ln(N_{eq})} + 0.049 \cdot \overline{ln(N_{eq})}^2 \Bigg]}}{q_u} </math> ||align="center"| (dimensionless)||align="right"|Equation 321.3.6.2 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''COV<sub>q<sub>u</sub></sub>'' = coefficient of variation for design value for uniaxial compressive strength of shale (dimensionless), | ||
| + | |||
| + | :''σ<sub>(q<sub>u</sub>)</sub>'' ≈ <math>\sqrt{{q_u}^2 \Bigg[1.654 + 1.882\frac{\sigma_{ln(\hat N_{eq})}^2}{n_s} - 0.503 \cdot \overline{ln(N_{eq})} + 0.049 \cdot \overline{ln(N_{eq})}^2 \Bigg]} </math> = standard deviation for design value of uniaxial compressive strength (consistent units), | ||
| + | |||
| + | :ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless), | ||
| + | |||
| + | :''q<sub>u</sub>'' = <math> e^{(1.354 \cdot \overline{ln (N_{eq})} - 3.587)}</math> = design value for uniaxial compressive strength of shale (ksf) determined from SPT measurements, | ||
| + | |||
| + | :<math> \overline{ln(N_{eq})}</math> = <math> \frac {\sum_{i=1}^n ln (\hat N_{eq})_i}{n_s}</math> = mean value of the natural log of ''N<sub>eq</sub>'' measurements in stratum of interest (consistent units), | ||
| + | |||
| + | |||
| + | :<math>ln (\hat N_{eq})_i </math> = natural log of measured value of ''N<sub>eq</sub>'' within stratum of interest (consistent units), | ||
| + | |||
| + | :''σ<sub>ln(N<sub>eq</sub>)</sub>'' = <math>\sqrt{\frac {\sum_{i=1}^n \Big(ln (\hat N_{eq})_i - \overline{ln(N_{eq})}\Big)^2}{n_s -1}}</math> = standard deviation of the natural log of ''N<sub>eq</sub>'' measurements in stratum of interest (consistent units), and | ||
| + | |||
| + | :''n<sub>s</sub>'' = number of ''N<sub>eq</sub>'' measurements within stratum of interest (dimensionless). | ||
| + | |||
| + | The value for ''q<sub>u</sub>'' shall be taken from Equation 321.3.6.1 based on the available ''N<sub>eq</sub>'' measurements in stratum of interest. Values for ''N<sub>eq</sub>'' shall be determined according to Equation Commentary 751.37.3.1 as described in [[751.37 Drilled Shafts#Commentary on EPG 751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)|EPG Commentary on 751.37.3.3]]. The standard deviation of the natural log of ''N<sub>eq</sub>'' measurements, ''σ<sub>ln(N<sub>eq</sub>)</sub>'', can be calculated from the equation provided, using the STDEV function in <br>Microsoft Excel<sup>©</sup> or similar functions in other computer programs. The empirical parameter ζ shall be determined according to the provisions of [[#321.3.5 Uncertainty Modifiers to Account for Quantity of Tests|EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests]]. | ||
| + | |||
| + | ==321.3.7 Design Values from Combined Direct and Surrogate Measurements== | ||
| + | {|style="padding: 0.3em; margin-left:10px; border:1px solid #ff0000; text-align:left; font-size: 95%; background:#f5f5f5" width="250px" align="right" | ||
| + | |- | ||
| + | |align="center"|'''[[#Commentary on EPG 321.3.7 Design Values from Combined Direct and Surrogate Measurements|Commentary for EPG 321.3.7 Design Values from Combined Direct and Surrogate Measurements''']] | ||
| + | |} | ||
| + | |||
| + | Design values for design parameters that can be established using both direct and surrogate measurements shall be established based on the respective mean and variance values established from consideration of the direct and surrogate measurements individually (as described in the provisions of EPG 321.3.6). | ||
| + | |||
| + | ===321.3.7.1 Establishing Mean Value from Combined Direct and Surrogate Measurements=== | ||
| + | |||
| + | Design values for parameters to be established from both direct and surrogate measurements within the stratum of interest shall be established as: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math> y = \overline y = \frac {\frac{\overline y_d}{\sigma_d^2} +\frac{\overline y_s}{\sigma_s^2}}{\frac {1}{\sigma_d^2}+\frac{1}{\sigma_s^2}} = \frac{\overline y_d \cdot \sigma_s^2 + \overline y_s \cdot \sigma_d^2}{\sigma_d^2 + \sigma_s^2} </math> ||align="center"| (consistent units)||align="right"|Equation 321.3.7.1 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''y'' = f(''x'') = design value for parameter of interest (consistent units), | ||
| + | |||
| + | :<math>\overline y</math> = mean value for design parameter of interest (consistent units), | ||
| + | |||
| + | :<math>\overline y_d</math> = mean value for design parameter of interest from available “direct” measurements (consistent units), | ||
| + | |||
| + | :<math>\sigma_d^2</math> = variance of mean value for design parameter of interest from available “direct” measurements (consistent units), | ||
| + | |||
| + | :<math>\overline y_s</math> = mean value for design parameter of interest from available “surrogate” measurements (consistent units), and | ||
| + | |||
| + | :<math>\sigma_s^2</math> = variance of mean value for design parameter of interest from available “surrogate” measurements (consistent units). | ||
| + | |||
| + | Values for <math>\overline y_d</math> and ''σ<sub>d</sub>'' respectively correspond to values for ''y'' and (''COV<sub>y</sub>∙y'') determined according to [[#321.3.2 Design Values for Strata with Constant Properties|EPG 321.3.2 Design Values for Strata with Constant Properties]] and shall be established according to the provisions of EPG 321.3.2. Similarly, values for <math>\overline y_s</math> and ''σ<sub>s</sub>'' respectively correspond to values for ''y'' and (''COV<sub>y</sub>∙y'') determined according to [[#321.3.6 Design Values from Surrogate Measurements|EPG 321.3.6 Design Values from Surrogate Measurements]] and shall be established according to the provisions of EPG 321.3.6. | ||
| + | |||
| + | ===321.3.7.2 Establishing COV Values from Combined Direct and Surrogate Measurements=== | ||
| + | |||
| + | The coefficient of variation of the mean value for the design parameter to be established from both direct and surrogate measurements within the stratum of interest shall be established as: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math> COV_y = \frac{\sigma_y}{y} = \frac {\sqrt{ \frac{\sigma_d^2 \cdot \sigma_s^2}{\sigma_d^2+\sigma_s^2}}}{y} </math> ||align="center"| (dimensionless)||align="right"|Equation 321.3.7.2 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''COV<sub>y</sub>'' = coefficient of variation for mean value of design parameter of interest (dimensionless), | ||
| + | |||
| + | :''σ<sub>y</sub>'' = <math> \sqrt{ \frac{\sigma_d^2 \cdot \sigma_s^2}{\sigma_d^2+\sigma_s^2}} </math> = standard deviation of the mean value of parameter of interest from both direct and surrogate measurements (consistent units), | ||
| + | |||
| + | :''y'' = design, or “model” value for parameter of interest (consistent units), | ||
| + | |||
| + | :<math>\sigma_d^2</math> = variance of mean value for design parameter of interest from available “direct” measurements (consistent units), and | ||
| + | |||
| + | :<math>\sigma_s^2</math> = variance of mean value for design parameter of interest from available “surrogate” measurements (consistent units). | ||
| + | |||
| + | The value for ''σ<sub>d</sub>'' corresponds to the value of (''COV<sub>y</sub>∙y'') determined according to [[#321.3.2 Design Values for Strata with Constant Properties|EPG 321.3.2 Design Values for Strata with Constant Properties]] and shall be established according to the provisions of EPG 321.3.2. Similarly, the value for ''σ<sub>s</sub>'' corresponds to the value for (''COV<sub>y</sub>∙y'') determined according to [[#321.3.6 Design Values from Surrogate Measurements|EPG 321.3.6 Design Values from Surrogate Measurements]] and shall be established according to the provisions of EPG 321.3.6. | ||
| + | |||
| + | ==321.3.8 References== | ||
| + | |||
| + | AASHTO (2009), ''AASHTO LRFD Bridge Design Specification: Customary U.S. Units'', American Association of State Highway and Transportation Officials, Fourth Edition with 2008 and 2009 Interim Revisions. | ||
| + | |||
| + | Ang, A.H-S, and W.H. Tang (1975), ''Probability Concepts in Engineering Planning and Design'', John Wiley and Sons, 409 pp. | ||
| + | |||
| + | Likos, W.J., L. Ge, D. Ding, S. Onyejekwe, M.D. Pierce, S.A. Grant, J.E. Loehr, and R.W. Stephenson (2011a), ''MoDOT Transportation Geotechnics Research Program: Laboratory Site Characterization Testing Program Data Report'', Missouri Department of Transportation, OR11.XXX, XXX pp. | ||
| + | |||
| + | Likos, W.J., J.E. Loehr, N. Maerz, K.A. Magner, L. Ge, and R.W. Stephenson (2011b), ''MoDOT Transportation Geotechnics Research Program: Site Characterization Program Interpretation Report'', Missouri Department of Transportation, OR11.XXX, XXX pp. | ||
| + | |||
| + | Loehr, J.E., A.Z. Boeckmann, P.L. Speckman, and D. Ding (2013), ''Procedures for Establishing Geotechnical Design Parameters from Two Data Sources'', Final Project Report submitted to Missouri Department of Transportation, 22 pp.. | ||
| + | |||
| + | Magner, K.A, N. Maerz, J.J. Bowders, M.D. Pierce, and J.E. Loehr (2011), ''MoDOT Transportation Geotechnics Research Program: Field Site Characterization Testing Program Data Report'', Missouri Department of Transportation, OR11.XXX, XXX pp. | ||
| + | |||
| + | |||
| + | ==321.3.9 Commentary== | ||
| + | |||
| + | These guidelines were developed based on a comprehensive research program conducted to improve design of bridge foundations and earth slopes. The methods provided in these provisions were established by combining theoretical considerations of parameter variability as well as empirical observations from a broad evaluation of site characterization techniques performed as a part of the research program. Additional details regarding the site characterization aspects of the research program can be found in Likos et al. (2011a), Magner et al. (2011), and Likos et al. (2011b). | ||
| + | |||
| + | The provisions of [[751.37 Drilled Shafts|EPG 751.37 Drilled Shafts]], [[751.38 Spread Footings|EPG 751.38 Spread Footings]] and [[321.1 Design of Earth Slopes|EPG 321.1 Design of Earth Slopes]] were developed under the presumption that parameter values and coefficients of variation are established according to the provisions of this article. | ||
| + | |||
| + | ===Commentary on [[#321.3.1 General |EPG 321.3.1 General]]=== | ||
| + | |||
| + | Variability and uncertainty in design parameters depends on a number of factors that include the specific sampling and test method(s) utilized, the character of the specific site, and the quantity of sampling and testing performed. Variability and uncertainty also depends upon whether one is considering the variability of the measurements or the uncertainty in the actual or mean value of the parameter. The provisions of this article are intended for use in establishing the variability or uncertainty of the mean value of design parameters that are appropriate for use in EPG 751.37, EPG 751.38, and EPG 321.1. | ||
| + | |||
| + | ===Commentary on [[#321.3.1.1 Relevant Design Parameters|EPG 321.3.1.1 Relevant Design Parameters]]=== | ||
| + | |||
| + | Other design parameters may be required for specific EPG provisions. However, the parameters listed are those that require estimation of both the mean value and coefficient of variation for establishing resistance factor values. | ||
| + | |||
| + | ===Commentary on [[#321.3.1.2 Development of Design Profiles for Relevant Design Properties|EPG 321.3.1.2 Development of Design Profiles for Relevant Design Properties]]=== | ||
| + | |||
| + | It is important to recognize that design profiles established according to the provisions of this article are not unique. Establishing design profiles for application of methods provided in [[751.37 Drilled Shafts|EPG 751.37 Drilled Shafts]], [[751.38 Spread Footings|EPG 751.38 Spread Footings]] and [[321.1 Design of Earth Slopes|EPG 321.1 Design of Earth Slopes]] necessarily involves judgment on the part of the designer because the type, quality, and quantity of testing performed for different sites will differ. Furthermore, two designers may rationally choose to represent the same set of data using different design profiles. Such differences are inherent to site characterization with limited data. The procedures provided in this article were developed with this realization in mind and the variabilities and uncertainties established following the provisions of this article reflect this fact. | ||
| + | |||
| + | In general, designers should seek to establish design profiles that have the least variability and uncertainty (i.e. the lowest ''COV'') for the available data, because this will increase the efficiency of the specific design. However, designers must also consider the quality and quantity of available data, the criticality of the structure, and the potential cost implications of developing highly refined design profiles and balance these with the costs required to develop rational design profiles. | ||
| + | |||
| + | As shown in Figure 321.3.1.1 for Stratum I, Stratum IV, and Stratum V, the coefficient of variation of the mean value for a parameter is not strictly constant for strata deemed to have linearly varying parameter values. Within such strata, the coefficient of variation will tend to be smaller at depths where more measurements are available and larger at depths where fewer measurements are available (because the uncertainty is greater where fewer measurements are available). When measurements are evenly distributed throughout the stratum, the coefficient of variation will tend to be least near the middle of the stratum and greatest near the upper and lower boundaries of the stratum. Despite these predictable results, a constant coefficient of variation has been adopted in the relevant EPG provisions to simplify application of the provisions. Designers must therefore compute or select a reasonable average value of the coefficient of variation that generally reflects the variability and uncertainty in the mean value for the parameter of interest within the stratum. | ||
| + | |||
| + | ===Commentary on [[#321.3.1.3 Minimum Testing Requirements |EPG 321.3.1.3 Minimum Testing Requirements]]=== | ||
| + | |||
| + | No minimum quantities for tests are required to use the provisions of [[751.37 Drilled Shafts|EPG 751.37 Drilled Shafts]], [[751.38 Spread Footings|EPG 751.38 Spread Footings]] and [[321.1 Design of Earth Slopes|EPG 321.1 Design of Earth Slopes]]. This is a significant departure from current AASHTO LRFD design specifications, which generally use constant resistance factors under the assumption that a minimum level of site characterization will be conducted. Instead, EPG 751.37, EPG 751.38 and EPG 321.1 provide resistance factors that depend upon the variability and uncertainty present in specific design parameters, which is directly influenced by the quantity of test measurements that are available. The intent of this approach is to guide development of appropriate site characterization activities through consideration of costs for additional characterization and cost savings that may be realized due to reductions in uncertainty, rather than requiring some minimum level of characterization. It is important to note that all resistance factors provided in EPG 751.37, EPG 751.38 and EPG 321.1 are intended to produce the target levels of reliability established by MoDOT, regardless of the level of uncertainty in design parameters. As such, increasing the number of test measurements will not measurably change the reliability of the final design. However, since greater resistance factors can be used when variability and uncertainty is reduced, increasing the quantity of site characterization will often result in more efficient and cost effective designs because it will allow for use of greater resistance factors. The role of the designer therefore is one of using judgment to optimize the level of site characterization based on the costs required for additional site characterization and the cost savings that may be realized from additional characterization. | ||
| + | |||
| + | Throughout these provisions, the variability and uncertainty in a design parameter is represented using the coefficient of variation (''COV''). For a specific site, the predominant means for reducing the coefficient of variation for a design parameter is by increasing the number of measurements of that parameter. | ||
| + | |||
| + | While the EPG provisions do not include minimum testing requirements, the provisions do require estimation of a value for the coefficient of variation in order to establish appropriate resistance factors. The provisions of EPG 321.3 require a minimum of three measurements of a parameter in order to quantitatively establish a value for the coefficient of variation. In cases where less than three measurements are available for a given stratum, designers must estimate values for the coefficient of variation based on experience and judgment. The coefficient of variation can be conservatively estimated to be equal to 1.0. However, experience will likely show that this is an excessively conservative value for most design cases. When estimating values for the coefficient of variation, designers should consider both the criticality of a structure and the sensitivity of the resulting designs to changes in the coefficient of variation. When in doubt, relatively large values for the coefficient of variation should be assumed. | ||
| + | |||
| + | ===Commentary on [[#321.3.2 Design Values for Strata with Constant Properties |EPG 321.3.2 Design Values for Strata with Constant Properties]]=== | ||
| + | |||
| + | The provisions of this article are intended for use establishing design parameters for strata that are deemed to have properties that are practically uniform. At a given site, it is perfectly acceptable to establish one or more strata as having constant parameters and one or more different strata as having linearly varying parameters. In such cases, the provisions of this article shall be followed for strata having constant parameters and the provisions of [[#321.3.3 Design Values for Strata with Linearly Varying Properties |EPG 321.3.3 Design Values for Strata with Linearly Varying Properties]] shall be followed for strata having linearly varying parameters. | ||
| + | |||
| + | Given a set of parameter measurements, calculation of the mean value and the coefficient of variation for a design parameter is relatively straightforward. However, it is not uncommon to encounter cases where some measurements may contain “outliers” that may not reflect the actual value of the relevant design parameter. Such outliers can arise when testing errors are made, or when the stratum of interest contains “lenses” or “stringers” of material that may not be representative of the collective stratum. The question then becomes whether to include outlier measurements in the calculation of the mean and/or coefficient of variation of the design parameter. As a general rule, measurements should be disregarded (i.e. “thrown out”) with great caution, and only after careful deliberation of whether the measured value is truly an outlier. This is especially true when relatively few measurements are available for the stratum. If the designer truly believes that a measurement is inaccurate, or not representative of the broader stratum, then the measurement should be disregarded. However, if there is any doubt about whether the measurement is valid, it should generally be included in the calculations to establish the mean value and coefficient of variation for the parameter. Measurements should never be disregarded simply for the purpose of skewing the mean value or reducing the computed coefficient of variation. | ||
| + | |||
| + | ===Commentary on EPG 321.3.2.1 Establishing Mean Values for Strata with Constant Property=== | ||
| + | |||
| + | No commentary. | ||
| + | |||
| + | <div id="Commentary on EPG 321.3.2.2"></div> | ||
| + | ===Commentary on [[#321.3.2.2 Establishing COV Values for Strata with Constant Property |EPG 321.3.2.2 Establishing COV Values for Strata with Constant Property]]=== | ||
| + | |||
| + | These provisions are based on the assumption that the measurements are independent measurements (i.e. uncorrelated). While this assumption is seldom strictly satisfied, it is a practical and often conservative assumption to make. | ||
| + | |||
| + | ===Commentary on [[#321.3.3 Design Values for Strata with Linearly Varying Properties |EPG 321.3.3 Design Values for Strata with Linearly Varying Properties]]=== | ||
| + | |||
| + | The provisions of this article are intended for use establishing design parameters for strata that are deemed to have properties that vary linearly with depth or elevation across the stratum. At a given site, it is perfectly acceptable to establish one or more strata as having constant parameters and one or more different strata as having linearly varying parameters. In such cases, the provisions of this article shall be followed for strata having linearly varying parameters and the provisions of EPG 321.3.2 shall be followed for strata having constant parameters. | ||
| + | |||
| + | Given a set of parameter measurements, calculation of the mean value and the coefficient of variation for a design parameter is relatively straightforward. However, it is not uncommon to encounter cases where some measurements may contain “outliers” that may not reflect the actual value of the relevant design parameter. Such outliers can arise when testing errors are made, or when the stratum of interest contains “lenses” or “stringers” of material that may not be representative of the collective stratum. The question then becomes whether to include outlier measurements in the calculation of the mean and/or coefficient of variation of the design parameter. As a general rule, measurements should be disregarded (i.e. “thrown out”) with great caution, and only after careful deliberation of whether the measured value is truly an outlier. This is especially true when relatively few measurements are available for the stratum. If the designer truly believes that a measurement is inaccurate, or not representative of the broader stratum, then the measurement should be excluded from calculation of the mean and coefficient of variation. However, if there is any doubt about whether the measurement is valid, it should generally be included in the calculations to establish the mean value and coefficient of variation for the parameter. Measurements should never be excluded simply for the purpose of skewing the mean value or reducing the computed coefficient of variation. | ||
| + | |||
| + | ===Commentary on [[#321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property |EPG 321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property]]=== | ||
| + | |||
| + | It is anticipated that the least squares fitting function LINEST provided in Microsoft Excel<sup>©</sup> or other similar programs will most commonly be used to establish the linear fit to the available data. Additional guidance on the least squares fitting technique can be found in Ang and Tang (1975), or many other references on statistics. | ||
| + | |||
| + | ===Commentary on [[#321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property |EPG 321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property]]=== | ||
| + | |||
| + | The correlation coefficient, ''ρ'', is the correlation coefficient of the regression coefficients, m and b, and not the correlation coefficient of the measured parameter with depth or elevation. Unfortunately, the Microsoft Excel<sup>©</sup> LINEST function does not provide the correlation coefficient, ρ, needed for estimation of the coefficient of variation of the mean value of the parameter. The correlation coefficient can, however, be calculated from the least squares fit to the data with additional calculations that are beyond the scope of this commentary. Designers are encouraged to consult any of a number of available references on statistics, such as Ang and Tang (1975), for additional guidance on calculation of the correlation coefficient of regression coefficients. | ||
| + | |||
| + | The assumption of a correlation coefficient, ''ρ'', equal to 1.0 may be extremely conservative in some instances. Use of ''ρ'' = 1.0 may therefore be appropriate for establishing preliminary estimates for the coefficient of variation so that preliminary or initial trial designs can be determined. If such design are determined to be sensitive to the value of ''ρ'', the additional analysis required to establish the coefficient of variation may be justified. | ||
| + | |||
| + | ''COV<sub>y</sub>'' is dependent on the depth ''z'' used for the calculations, both because ''σ<sub>y</sub>'' is dependent upon ''z'' and because the mean value ''y'' is also dependent upon ''z''. For design purposes, a single value of the coefficient of variation must be chosen to reflect the nominal coefficient of variation across the entire stratum. In general, the ''COV'' will tend to be smaller near depths or elevations where measurements are available and greater at depths/elevations where few measurements exist. The coefficient of variation should therefore be computed for several depths/elevations within the stratum, and a nominal value for ''COV'' chosen to reflect the general variability of the mean value of the measurements. | ||
| + | |||
| + | ===Commentary on [[#321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters|EPG 321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters]]=== | ||
| + | |||
| + | Calculations required to establish design values for Mohr-Coulomb shear strength parameters, ''c'' and ''ϕ'', are similar to those required to establish design values for parameters that vary linearly over the depth of a stratum. The notable difference in the calculations is that the linear fit is performed for data reflecting shear strength as a function of either total or effective stress, rather than for data reflect a design parameter as a function of depth or elevation. | ||
| + | |||
| + | The provisions of this article require that data reflecting the normal stress and shear stress <u>on the failure plane at failure</u> be established for all test measurements and that these data be used to establish a best fit failure envelope and coefficient of variation of the shear strength. These values are respectively denoted as ''σ<sub>ff</sub>'' and ''τ<sub>ff</sub>'' for the normal stress and shear stress on the failure plane at failure. Calculation of ''σ<sub>ff</sub>'' and ''τ<sub>ff</sub>'' from direct shear tests is generally straightforward as ''σ<sub>ff</sub>'' is taken to be the vertical normal stress on the specimen at failure (i.e. the normal load divided by the specimen area at failure) and ''τ<sub>ff</sub>'' is taken to be the shear stress on the horizontal plane at failure (i.e. the shear load divided by the specimen area at failure). Values for ''σ<sub>ff</sub>'' and ''τ<sub>ff</sub>'' can also be established from results of triaxial tests as follows: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math> \sigma_{ff} = \frac{(\sigma_{1f} + \sigma_{3f})}{2} - \frac{(\sigma_{1f} - \sigma_{3f})}{2}sin\phi </math> ||align="center"| (consistent units)||align="right"|Equation Commentary 321.3.4.1 | ||
| + | |- | ||
| + | |align="left"|<math> \tau_{ff} = \frac{(\sigma_{1f} - \sigma_{3f})}{2} cos\phi </math> ||align="center"| (consistent units)||align="right"|Equation Commentary 321.3.4.2 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''σ<sub>ff</sub>'' = total normal stress on the failure plane at failure (consistent units of stress), | ||
| + | |||
| + | :''τ<sub>ff</sub>'' = shear stress on the failure plane at failure (consistent units of stress), | ||
| + | |||
| + | :''σ<sub>1f</sub>'' = total major principal stress at failure (consistent units of stress), | ||
| + | |||
| + | :''σ<sub>3f</sub>'' = total minor principal stress at failure (consistent units of stress), and | ||
| + | |||
| + | :''ϕ'' = Mohr-Coulomb angle of internal friction in terms of total stresses (degrees). | ||
| + | |||
| + | For effective stress analyses, values for <math>\overline \sigma_{ff}</math> and ''τ<sub>ff</sub>'' can be similarly established as: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|<math> \overline \sigma_{ff} = \frac{(\overline \sigma_{1f} + \overline \sigma_{3f})}{2} - \frac{(\sigma_{1f} - \sigma_{3f})}{2}sin\overline \phi </math> ||align="center"| (consistent units)||align="right"|Equation Commentary 321.3.4.3 | ||
| + | |- | ||
| + | |align="left"|<math> \tau_{ff} = \frac{(\sigma_{1f} - \sigma_{3f})}{2} cos\overline \phi </math> ||align="center"| (consistent units)||align="right"|Equation Commentary 321.3.4.4 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math> \overline \sigma_{ff}</math> = effective normal stress on the failure plane at failure (consistent units of stress), | ||
| + | |||
| + | :''τ<sub>ff</sub>'' = shear stress on the failure plane at failure (consistent units of stress), | ||
| + | |||
| + | :<math> \overline \sigma_{1f}</math> = effective major principal stress at failure (consistent units of stress), | ||
| + | |||
| + | :<math> \overline \sigma_{3f}</math> = effective minor principal stress at failure (consistent units of stress), and | ||
| + | |||
| + | :<math> \overline \phi</math> = Mohr-Coulomb angle of internal friction in terms of effective stresses (degrees). | ||
| + | |||
| + | Calculation of the normal and shear stress on the failure plane at failure requires knowledge of the angle of internal friction (''ϕ''), in terms of either total or effective stresses. However, the value for ''ϕ'' or <math> \overline \phi</math> is not known until the best fit relationship is established so an iterative calculation is required wherein an estimate of the angle of internal friction is first assumed, from which trial values for ''σ<sub>ff</sub>'' and ''τ<sub>ff</sub>'' can be established. These trial values for ''σ<sub>ff</sub>'' and ''τ<sub>ff</sub>'' can then be used to determine a best fit failure envelope. The angle of internal friction from this envelope should be compared to the one originally assumed to calculate ''σ<sub>ff</sub>'' and ''τ<sub>ff</sub>''. If the values are different, the calculations should be iteratively repeated until the assumed value of the friction angle is practically equal to the friction angle produced from the least squares best fit calculations. | ||
| + | |||
| + | ===Commentary on EPG 321.3.4.1 Establishing Mean Values for ''c'' and ''ϕ'' in Terms of Total Stresses=== | ||
| + | |||
| + | No commentary. | ||
| + | |||
| + | ===Commentary on EPG 321.3.4.2 Establishing Mean Values for '''<math> \overline c</math>''' and '''<math> \overline \phi</math>''' in Terms of Effective Stresses=== | ||
| + | |||
| + | No commentary. | ||
| + | |||
| + | ===Commentary on [[#321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters|EPG 321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters]]=== | ||
| + | |||
| + | The correlation coefficient, ''ρ'', is the correlation coefficient of the regression coefficients, tan''ϕ'' and ''c'' or tan<math>\overline \phi</math> and <math> \overline c</math>, and not the correlation coefficient of the measured values of shear strength with total or effective normal stress. Unfortunately, the Microsoft Excel<sup>©</sup> LINEST function does not provide the correlation coefficient, ''ρ'', needed for estimation of the coefficient of variation of the mean value of the parameter. The correlation coefficient can, however, be calculated from the least squares fit to the data with additional calculations that are beyond the scope of this commentary. Designers are encouraged to consult any of a number of available references on statistics, such as Ang and Tang (1975), for additional guidance on calculation of the correlation coefficient. | ||
| + | |||
| + | The assumption of a correlation coefficient, ''ρ'', equal to 1.0 may be extremely conservative in some instances. Use of ''ρ'' = 1.0 may therefore be appropriate for establishing preliminary estimates for the coefficient of variation so that preliminary or initial trial designs can be determined. If such design are determined to be sensitive to the value of ''ρ'', the additional analysis required to establish the coefficient of variation may be justified. | ||
| + | |||
| + | ''COV<sub>ss</sub>'' is dependent on the total or effective normal stress, ''σ'' or <math> \overline \sigma</math>, used for the calculations, both because ''σ<sub>ss</sub>'' is dependent upon ''σ'' or <math> \overline \sigma</math> and because the mean value s is also dependent upon ''σ'' or <math> \overline \sigma</math>. For design purposes, a single value of the coefficient of variation must be chosen to reflect the nominal coefficient of variation across the range in total or effective normal stresses for which the strength envelope will be used. In general, the ''COV'' will tend to be smaller at normal stresses where measurements are available and greater at normal stresses where few measurements exist. The coefficient of variation should therefore be computed for a range of normal stresses appropriate for the problem being considered, and a nominal value for ''COV'' chosen to reflect the general variability of the mean value of the measurements. | ||
| + | |||
| + | ===Commentary on [[#321.3.5 Uncertainty Modifiers to Account for Quantity of Tests|EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests]]=== | ||
| + | |||
| + | The empirical modifier, ζ, in essence imposes a penalty to account for the fact that the variability and uncertainty derived from a set of measurements may underestimate the actual variability and uncertainty present at a site. Because underestimating the coefficient of variation will produce unconservative designs, the modifier is introduced to avoid the rare case where the coefficient of variation derived from a set of measurements may dramatically under-represent the actual variability and uncertainty that is present in the overall population. The likelihood of this occurring is greatest when there are few measurements and lessens dramatically with increasing numbers of measurements. The modifier is thus greatest for small numbers of measurements and decreases with increasing numbers of measurements. | ||
| + | |||
| + | The possibility also exists for obtaining an unrealistically large value for the coefficient of variation from a specific set of measurements. Such a result would produce a conservative design since it would produce a resistance factor that is generally less than what would be required if the actual population coefficient of variation were know. However, since it is not possible to know whether the coefficient of variation calculated from a specific set of measurements is accurate, conservative, or unconservative, prudence requires that the modifier be applied in all cases to avoid unconservative results that might produce performance problems. | ||
| + | |||
| + | The modifiers provided in EPG 321.3.5 are empirical in the sense that the modifier values were established from analyses of empirical measurements of relevant design parameters for several sites that are generally representative of conditions encountered by MoDOT for design of bridges and other structures (Likos et al., 2011b). The analyses performed consisted of a series of hypothetical sampling cases from extensive sets of measurements to evaluate the range of potential errors that may be introduced for different quantities of measurements. From these analyses, modifiers were established using judgment so that the likelihood of calculating an unrealistically low value for the coefficient of variation would be small. These analyses were performed using measurements of all design parameters utilized within [[751.37 Drilled Shafts|EPG 751.37 Drilled Shafts]], [[751.38 Spread Footings|EPG 751.38 Spread Footings]] and [[321.1 Design of Earth Slopes|EPG 321.1 Design of Earth Slopes]]. The modifiers provided in EPG 321.3.5 reflect a nominal fit to the collection of curves produced from these analyses so that a single modifier could be used for all design parameters. It is also possible to produce a series of modifiers, each reflecting the relationship for a different design parameter. However, this approach was not adopted in order to keep application of the empirical modifier as straightforward as possible. | ||
| + | |||
| + | ===Commentary on [[#321.3.6 Design Values from Surrogate Measurements|EPG 321.3.6 Design Values from Surrogate Measurements]]=== | ||
| + | |||
| + | The provisions of this article are derived from work described in Loehr et al. (2013). Common examples of surrogate measurements include use of Standard Penetration Test measurements or Cone Penetration Test Measurements to establish design parameters, which generally require application of an empirical relationship between the surrogate measurement and the design parameter of interest (e.g. SPT blow counts and uniaxial compressive strength). Such correlations introduce uncertainty into estimation of the mean and the coefficient of variation of the mean for a parameter, in addition to the variability and uncertainty in the measurements themselves, that must be accounted for in establishing appropriate design values for a parameter of interest. | ||
| + | |||
| + | The provisions of this article presume that there is a linear relationship between the surrogate measurement and the parameter of interest of the form: | ||
| + | |||
| + | {| style="margin: 1em auto 1em auto" width="800" | ||
| + | |- | ||
| + | |align="left"|''y = β<sub>0</sub> + β<sub>1</sub>x'' ||align="center"| (consistent units)||align="right"|Equation Commentary 321.3.6.1 | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | :''y'' = f(''x'') = value for parameter of interest (consistent units), | ||
| + | |||
| + | :''x'' = value of the surrogate measurement (consistent units), | ||
| + | |||
| + | :''β<sub>0</sub>'' = y-intercept of linear relation between surrogate measurement and parameter of interest (consistent units), and | ||
| + | |||
| + | :''β<sub>1</sub>'' = slope of linear relation between surrogate measurement and parameter of interest (consistent units). | ||
| + | |||
| + | Such linear relations are common. In cases where the relationship between a surrogate measurement and the parameter of interest is non-linear, similar methods can be applied for transformed values of the surrogate and/or parameter of interest that serve to “linearize” the relationship as described in Loehr et al (2013). | ||
| + | |||
| + | The methods described in Loehr et al. (2013) can be applied to a wide range of geotechnical design parameters and to different surrogate measurements. At present, specific equations have only been developed for establishing design values for the uniaxial compressive strength (q_u) of shale from SPT measurements (N_eq). It is anticipated that additional provisions will be developed in the future for other design parameters and other surrogate measurements. | ||
| + | |||
| + | ===Commentary on [[#321.3.6.1 Establishing Mean Value of qu from Standard Penetration Tests in Shale|EPG 321.3.6.1 Establishing Mean Value of q<sub>u</sub> from Standard Penetration Tests in Shale]]=== | ||
| + | |||
| + | The provisions of this article were derived from the work described in Loehr et al. (2013), using results from regression performed using a natural logarithm transformation of both the direct (''q<sub>u</sub>'') and surrogate (''N<sub>eq</sub>'') measurements. While such transformations complicate the equations slightly, use of untransformed measurements produces an equation with such great variability and uncertainty that SPT measurements are rendered practically useless. The additional complication introduced by the logarithmic transformation is therefore necessary if some value is to be derived from use of SPT measurements for establishing design values for ''q<sub>u</sub>''. | ||
| + | |||
| + | It is important to emphasize that the mean of the natural logarithm of a set of numbers is not the same as the natural logarithm of the mean of the same set of numbers. Thus, when applying the provisions of this article, the natural logarithm of the individual ''N<sub>eq</sub>'' measurements must be taken prior to computing the mean of the log transformed values. It is not acceptable to take the natural logarithm of the mean of the ''N<sub>eq</sub>'' measurements. | ||
| + | |||
| + | ===Commentary on [[#321.3.6.2 Establishing COV Values for qu from Standard Penetration Tests in Shale|EPG 321.3.6.2 Establishing COV Values for q<sub>u</sub> from Standard Penetration Tests in Shale]]=== | ||
| + | |||
| + | The provisions of this article were derived from the work described in Loehr et al. (2013), using results from regression performed using a natural logarithm transformation of both the direct (''q<sub>u</sub>'') and surrogate (''N<sub>eq</sub>'') measurements. While such transformations complicate the equations slightly, use of untransformed measurements produces an equation with such great variability and uncertainty that SPT measurements are rendered practically useless. The additional complication introduced by the logarithmic transformation is therefore necessary if some value is to be derived from use of SPT measurements for establishing design values for ''q<sub>u</sub>''. | ||
| + | |||
| + | It is important to emphasize that the mean of the natural logarithm of a set of numbers is not the same as the natural logarithm of the mean of the same set of numbers. Thus, when applying the provisions of this article, the natural logarithm of the individual ''N<sub>eq</sub>'' measurements must be taken prior to computing the mean of the log transformed values. It is not acceptable to take the natural logarithm of the mean of the ''N<sub>eq</sub>'' measurements. | ||
| + | |||
| + | ===Commentary on [[#321.3.7 Design Values from Combined Direct and Surrogate Measurements|EPG 321.3.7 Design Values from Combined Direct and Surrogate Measurements]]=== | ||
| + | |||
| + | The provisions of this article were established from the work described in Loehr et al. (2013). These provisions can be applied to a number of different design parameters where both direct and surrogate measurements are available. | ||
| + | |||
| + | |||
[[Category: 321 Geotechnical Engineering]] | [[Category: 321 Geotechnical Engineering]] | ||
Latest revision as of 08:03, 19 June 2019
Methods provided for design of drilled shafts, design of spread footings and design of earth slopes require that both values for design parameters and values for coefficients of variation for the design parameters be established. The provisions of this article provide procedures for establishing design parameter values and design parameter uncertainty for use with these provisions.
Contents
- 1 321.3.1 General
- 2 321.3.2 Design Values for Strata with Constant Properties
- 3 321.3.3 Design Values for Strata with Linearly Varying Properties
- 4 321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters
- 5 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests
- 6 321.3.6 Design Values from Surrogate Measurements
- 7 321.3.7 Design Values from Combined Direct and Surrogate Measurements
- 8 321.3.8 References
- 9 321.3.9 Commentary
- 9.1 Commentary on EPG 321.3.1 General
- 9.2 Commentary on EPG 321.3.1.1 Relevant Design Parameters
- 9.3 Commentary on EPG 321.3.1.2 Development of Design Profiles for Relevant Design Properties
- 9.4 Commentary on EPG 321.3.1.3 Minimum Testing Requirements
- 9.5 Commentary on EPG 321.3.2 Design Values for Strata with Constant Properties
- 9.6 Commentary on EPG 321.3.2.1 Establishing Mean Values for Strata with Constant Property
- 9.7 Commentary on EPG 321.3.2.2 Establishing COV Values for Strata with Constant Property
- 9.8 Commentary on EPG 321.3.3 Design Values for Strata with Linearly Varying Properties
- 9.9 Commentary on EPG 321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property
- 9.10 Commentary on EPG 321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property
- 9.11 Commentary on EPG 321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters
- 9.12 Commentary on EPG 321.3.4.1 Establishing Mean Values for c and ϕ in Terms of Total Stresses
- 9.13 Commentary on EPG 321.3.4.2 Establishing Mean Values for and in Terms of Effective Stresses
- 9.14 Commentary on EPG 321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters
- 9.15 Commentary on EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests
- 9.16 Commentary on EPG 321.3.6 Design Values from Surrogate Measurements
- 9.17 Commentary on EPG 321.3.6.1 Establishing Mean Value of qu from Standard Penetration Tests in Shale
- 9.18 Commentary on EPG 321.3.6.2 Establishing COV Values for qu from Standard Penetration Tests in Shale
- 9.19 Commentary on EPG 321.3.7 Design Values from Combined Direct and Surrogate Measurements
321.3.1 General
| Commentary for EPG 321.3.1 General |
Provisions of EPG 751.37 Drilled Shafts, EPG 751.38 Spread Footings and EPG 321.1 Design of Earth Slopes were developed presuming that the design parameter values used for the provisions are mean values of the relevant parameters. These EPG provisions also require that the coefficients of variation for the design parameters be established to reflect the variability and uncertainty present in the design parameters. Methods for establishing both mean values and coefficients of variation for design parameters for relevant strata are provided in these provisions.
321.3.1.1 Relevant Design Parameters
| Commentary for EPG 321.3.1.1 Relevant Design Parameters |
Design parameters that require estimation of mean values and values for the coefficient of variation in EPG 751.37, EPG 751.38 and EPG 321.1 include those shown in Table 321.3.1.1
| Design Parameter | Relevant EPG Article(s) | |
|---|---|---|
| Nomenclature | Description | |
| qu | uniaxial compressive strength of rock | 751.37.3.1, 751.37.3.2 751.37.4.1, 751.37.4.2 751.38.3.1, 751.38.3.2 751.38.4.1, 751.38.4.2 |
| su | undrained shear strength | 321.1.2.4, 751.37.3.6 751.37.4.1, 751.37.4.2 751.38.3.3 |
| c | total stress cohesion intercept | 321.1.2.4 |
| tan ϕ | tangent of total stress friction angle | 321.1.2.4 |
| effective stress cohesion intercept | 321.1.2.5 | |
| tan | tangent of effective stress friction angle | 321.1.2.5 |
| cc | compression index | 321.1.3.2, 751.38.4.3 |
| cr | recompression index | 321.1.3.2, 751.38.4.3 |
| σ'p | pre-consolidation stress | 321.1.3.2, 751.38.4.3 |
| Neq | equivalent SPT N-value | 751.37.3.3, 751.37.4.1 751.37.4.2 |
| TCP | penetration from Texas Cone Penetration test | 751.37.3.4, 751.37.4.1 751.37.4.2 |
| Is(50) | corrected point load index | 751.37.3.5, 751.37.4.1 751.37.4.2 |
321.3.1.2 Development of Design Profiles for Relevant Design Properties
| Commentary for EPG 321.3.1.2 Development of Design Profiles for Relevant Design Properties |
The provisions of this article are intended to produce rational “design profiles” of properties needed for application of EPG 751.37 Drilled Shafts, EPG 751.38 Spread Footings and EPG 321.1 Design of Earth Slopes. These design profiles establish a model for how a parameter varies with depth or elevation, as well as the variability or uncertainty associated with the model.
For the purposes of this provision, design profiles are assumed to be composed of a number of individual strata. The design parameter within an individual stratum is assumed to have values that are either constant, or linearly varying with depth or elevation as illustrated in Fig. 321.3.1.1. All design profiles can be reasonably represented as some combination of strata that have either a constant property or linearly varying property within each stratum. Regardless of whether the parameter value is assumed to be constant or linearly varying with depth, the variability or uncertainty in the parameter value within a single stratum is assumed to be constant, and represented by a constant value of the coefficient of variation (COV).
321.3.1.3 Minimum Testing Requirements
| Commentary for EPG 321.3.1.3 Minimum Testing Requirements |
Method provided in this article and EPG 751.37, EPG 751.38 and EPG 321.1 were developed to accurately account for variability and uncertainty associated with geotechnical design parameters regardless of the quantity of testing performed. However, the methods provided in this article require a minimum of three measurements within each stratum for application of the methods. For cases where fewer than three measurements are available for a particular stratum, designers must resort to use of judgment for estimation of the coefficient of variation as described in the commentary to these guidelines.
321.3.2 Design Values for Strata with Constant Properties
| Commentary for EPG 321.3.2 Design Values for Strata with Constant Properties |
The provisions of this article shall be satisfied when the parameter of interest is deemed to be constant over the stratum of interest.
321.3.2.1 Establishing Mean Values for Strata with Constant Property
Design values for parameters in strata that are judged to have practically constant or uniform values for the parameter of interest shall be established as the arithmetic mean of the available measurements:
| (consistent units) | Equation 321.3.2.1 |
where:
- y = design, or “model” value for parameter of interest (consistent units),
- = mean value of parameter from a set of measurements (consistent units),
- = measured value of the parameter of interest (consistent units) and
- n = number of available measurements used to establish the mean value (dimensionless).
The mean value of the relevant parameter can be calculated from all measured values using the AVERAGE function in Microsoft Excel© or similar functions in other computer programs.
321.3.2.2 Establishing COV Values for Strata with Constant Property
| Commentary on EPG 321.3.2.2 Establishing COV Values for Strata with Constant Property |
The coefficient of variation of the mean value for the design parameter shall be established from the set of available measurements as:
| (dimensionless) | Equation 321.3.2.2 |
where:
- 𝐶𝑂𝑉𝑦 = coefficient of variation for mean value of design parameter of interest (dimensionless),
- = standard deviation of the mean value of parameter of interest (consistent units),
- = empirical modifier to account for effects of quantity of tests (dimensionless),
- y = design, or “model” value for parameter of interest (consistent units),
- = standard deviation of measurements of parameter of interest (consistent units),
- n = number of available measurements used to establish the mean value (dimensionless) and
- = measured value of a parameter of interest (consistent units).
The standard deviation of the measurements, , can be calculated from the equation provided using the STDEV function in Microsoft Excel© or similar functions in other computer programs. The empirical parameter shall be determined as provided in EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests.
321.3.3 Design Values for Strata with Linearly Varying Properties
| Commentary for EPG 321.3.3 Design Values for Strata with Linearly Varying Properties |
The provisions of this article shall be satisfied when the property of interest is deemed to vary linearly with depth or elevation over the stratum of interest.
321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property
| Commentary for EPG 321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property |
Design values for parameters in strata where the property of interest is judged to vary linearly with depth or elevation shall be established from a linear best fit relation to the available measurements:
| y = b + mz | (consistent units) | Equation 321.3.3.1 |
where
- y = f(z) = design, or “model” value for parameter of interest (consistent units),
- z = depth or elevation (consistent units of length),
- b = intercept from linear least squares fit to the available data (consistent units) and
- m = slope from linear least squares fit to the available data (consistent units).
The coefficients m and b can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs.
321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property
| Commentary for EPG 321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property |
The coefficient of variation of the mean value for the design parameter shall be established from the set of available measurements as:
| (dimensionless) | Equation 321.3.3.2 |
where
- COVy = coefficient of variation for mean value of design parameter of interest (dimensionless),
- = standard deviation of the mean value of parameter of interest (consistent units),
- = empirical modifier to account for effects of quantity of tests (dimensionless),
- y = b + mz = mean value of parameter from the set of measurements (consistent units),
- z = depth or elevation (consistent units of length),
- σm = standard error in the slope, m, of the least squares fit (consistent units),
- σb = standard error in the intercept, b, of the least squares fit (consistent units) and
- = correlation coefficient for m and b from the least squares fit (dimensionless).
The standard errors for the slope and intercept of the least squares fit (σm and σb) can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs. The empirical parameter shall be determined as provided in EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests. The correlation coefficient 𝜌 can be determined using method described in the accompanying commentary document, or can conservatively be assumed to be equal to 1.0.
Since COVy from Equation 321.3.3.2 varies with depth or elevation, z, a nominal average value for COVy shall be selected and used for design. This average value can be calculated as a rigorous average of value computed over the depth or elevation range for the stratum, or can be selected by judgment based on values computed over the depth or elevation range of the stratum.
321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters
| Commentary for EPG 321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters |
The provisions of this article shall be satisfied when establishing design values for Mohr-Coulomb shear strength parameters, c and ϕ. This is the case for Mohr-Coulomb shear strength parameters established in terms of total stresses, i.e. c and ϕ, or for Mohr-Coulomb shear strength parameters established in terms of effective stresses, i.e. and . In all cases such parameters will be presumed to be constant over a particular stratum; assigning linearly varying values of c and/or ϕ within a single stratum is not permitted.
321.3.4.1 Establishing Mean Values for c and ϕ in Terms of Total Stresses
Design values for c and ϕ for total stress analyses shall be established from a linear best fit relation to the available shear strength measurements made at different total confining stresses (e.g. from unconsolidated-undrained type triaxial tests). The best fit linear relation will be of the form:
| s = c + σtanϕ | (consistent units) | Equation 321.3.4.1 |
where
- s = f(σ) = design, or “model” value for shear strength in terms of total stresses (consistent units of stress),
- σ = total stress (consistent units of stress),
- c = total stress “cohesion intercept” from linear least squares fit to the available data (consistent units of stress), and
- tanϕ = slope of failure envelope from linear least squares fit to the available data (dimensionless).
The coefficients c and tanϕ can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs where the function is fit to data reflecting the shear stress and total normal stress on the failure plane at failure as described in the commentary to this article.
321.3.4.2 Establishing Mean Values for and in Terms of Effective Stresses
Design values for and for effective stress analyses shall be established from a linear best fit relation to the available shear strength measurements made at different effective confining stresses (e.g. from direct shear tests or from consolidated-drained or consolidated-undrained type triaxial tests). The best fit linear relation will be of the form:
| s = tan | (consistent units) | Equation 321.3.4.2 |
where
- s = f() = design, or “model” value for shear strength in terms of effective stresses (consistent units of stress),
- = effective stress (consistent units of stress),
- = effective stress “cohesion intercept” from linear least squares fit to the available data (consistent units of stress), and
- tan = slope of failure envelope from linear least squares fit to the available data (dimensionless).
The coefficients and tan can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs where the function is fit to data reflecting the shear stress and effective normal stress on the failure plane at failure as described in the commentary to this article.
321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters
| Commentary for EPG 321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters |
The coefficient of variation for the mean value of shear strength computed from Mohr-Coulomb shear strength parameters shall be established from the set of available measurements. If the measurements are in terms of total stresses, the coefficient of variation shall be calculated as:
| (dimensionless) | Equation 321.3.4.3 |
where
- COVss = coefficient of variation for mean value of shear strength (dimensionless),
- σss = = standard deviation of the mean value of shear strength (consistent units of stress),
- ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless),
- s = c + σ tanϕ = mean value of shear strength from the set of measurements (consistent units of stress),
- σ = total stress (consistent units of stress),
- σtanϕ = standard error in the slope, tanϕ, of the least squares fit (dimensionless),
- σc = standard error in the intercept, c, of the least squares fit (consistent units), and
- ρ = correlation coefficient for tanϕ and c from the least squares fit (dimensionless).
The standard errors for the slope and intercept of the least squares fit (σtanϕ and σc) can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs. The empirical parameter ζ shall be determined as provided in EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests. The correlation coefficient ρ can be determined using methods described in the accompanying commentary document, or can conservatively be assumed to be equal to 1.0.
If the measurements are in terms of effective stresses, the coefficient of variation shall be similarly calculated as:
| (dimensionless) | Equation 321.3.4.4 |
where
- COVss = coefficient of variation for mean value of shear strength (dimensionless),
- σss = = standard deviation of the mean value of shear strength (consistent units of stress),
- ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless),
- s = = mean value of shear strength from the set of measurements (consistent units of stress),
- = effective stress (consistent units of stress),
- = standard error in the slope, tan, of the least squares fit (dimensionless),
- = standard error in the intercept, , of the least squares fit (consistent units), and
- ρ = correlation coefficient for tan and from the least squares fit (dimensionless).
The standard errors for the slope and intercept of the least squares fit ( and ) can be determined using the LINEST function in Microsoft Excel© or similar functions in other computer programs. The empirical parameter ζ shall be determined as provided in EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests. The correlation coefficient ρ can be determined using methods described in the accompanying commentary document, or can conservatively be assumed to be equal to 1.0.
Since COVss from Equations 321.3.4.3 or 321.3.4.4 varies with the value of total stress, σ, or effective stress, , a nominal average value for COVss shall be selected and used for design. This average value can be calculated as a rigorous average of value computed over the range of total stresses that are relevant for the particular design problem, or can be selected by judgment based on values computed over the appropriate range of normal stress.
321.3.5 Uncertainty Modifiers to Account for Quantity of Tests
| Commentary for EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests |
The empirical uncertainty modifier in Equations 321.3.2.2, 321.3.3.2, 321.3.4.3 and 321.3.4.4 shall be determined from Fig. 321.3.5.1 or calculated as
| (dimensionless) | Equation 321.3.5.1 |
where
- ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless), and
- n = number of available measurements (dimensionless).
321.3.6 Design Values from Surrogate Measurements
| Commentary for EPG 321.3.6 Design Values from Surrogate Measurements |
The provisions of this article shall be satisfied when the parameter of interest is determined from “surrogate” measurements rather than from “direct” measurement of the parameter. The specific provisions to be satisfied depend on both the specific type of surrogate measurement and the specific design parameter of interest.
321.3.6.1 Establishing Mean Value of qu from Standard Penetration Tests in Shale
| Commentary for EPG 321.3.6.1 Establishing Mean Value of qu from Standard Penetration Tests in Shale |
Design values for the uniaxial compressive strength, qu, of a specific shale stratum can be established from Standard Penetration Test (SPT) measurements in that stratum as:
| (ksf) | Equation 321.3.6.1 |
where
- qu = f() = design value for uniaxial compressive strength of shale (ksf), and
- = mean value of the natural log of Neq measurements in stratum of interest (consistent units).
Values for Neq shall be determined according to Equation Commentary 751.37.3.1 as described in EPG Commentary on 751.37.3.3.
321.3.6.2 Establishing COV Values for qu from Standard Penetration Tests in Shale
| Commentary for EPG 321.3.6.2 Establishing COV Values of qu from Standard Penetration Tests in Shale |
The coefficient of variation of the design value for qu shall be established from the set of available Neq measurements within the stratum of interest as:
| (dimensionless) | Equation 321.3.6.2 |
where
- COVqu = coefficient of variation for design value for uniaxial compressive strength of shale (dimensionless),
- σ(qu) ≈ = standard deviation for design value of uniaxial compressive strength (consistent units),
- ζ = empirical modifier to account for effects attributed to the quantity of tests (dimensionless),
- qu = = design value for uniaxial compressive strength of shale (ksf) determined from SPT measurements,
- = = mean value of the natural log of Neq measurements in stratum of interest (consistent units),
- = natural log of measured value of Neq within stratum of interest (consistent units),
- σln(Neq) = = standard deviation of the natural log of Neq measurements in stratum of interest (consistent units), and
- ns = number of Neq measurements within stratum of interest (dimensionless).
The value for qu shall be taken from Equation 321.3.6.1 based on the available Neq measurements in stratum of interest. Values for Neq shall be determined according to Equation Commentary 751.37.3.1 as described in EPG Commentary on 751.37.3.3. The standard deviation of the natural log of Neq measurements, σln(Neq), can be calculated from the equation provided, using the STDEV function in
Microsoft Excel© or similar functions in other computer programs. The empirical parameter ζ shall be determined according to the provisions of EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests.
321.3.7 Design Values from Combined Direct and Surrogate Measurements
| Commentary for EPG 321.3.7 Design Values from Combined Direct and Surrogate Measurements |
Design values for design parameters that can be established using both direct and surrogate measurements shall be established based on the respective mean and variance values established from consideration of the direct and surrogate measurements individually (as described in the provisions of EPG 321.3.6).
321.3.7.1 Establishing Mean Value from Combined Direct and Surrogate Measurements
Design values for parameters to be established from both direct and surrogate measurements within the stratum of interest shall be established as:
| (consistent units) | Equation 321.3.7.1 |
where
- y = f(x) = design value for parameter of interest (consistent units),
- = mean value for design parameter of interest (consistent units),
- = mean value for design parameter of interest from available “direct” measurements (consistent units),
- = variance of mean value for design parameter of interest from available “direct” measurements (consistent units),
- = mean value for design parameter of interest from available “surrogate” measurements (consistent units), and
- = variance of mean value for design parameter of interest from available “surrogate” measurements (consistent units).
Values for and σd respectively correspond to values for y and (COVy∙y) determined according to EPG 321.3.2 Design Values for Strata with Constant Properties and shall be established according to the provisions of EPG 321.3.2. Similarly, values for and σs respectively correspond to values for y and (COVy∙y) determined according to EPG 321.3.6 Design Values from Surrogate Measurements and shall be established according to the provisions of EPG 321.3.6.
321.3.7.2 Establishing COV Values from Combined Direct and Surrogate Measurements
The coefficient of variation of the mean value for the design parameter to be established from both direct and surrogate measurements within the stratum of interest shall be established as:
| (dimensionless) | Equation 321.3.7.2 |
where
- COVy = coefficient of variation for mean value of design parameter of interest (dimensionless),
- σy = = standard deviation of the mean value of parameter of interest from both direct and surrogate measurements (consistent units),
- y = design, or “model” value for parameter of interest (consistent units),
- = variance of mean value for design parameter of interest from available “direct” measurements (consistent units), and
- = variance of mean value for design parameter of interest from available “surrogate” measurements (consistent units).
The value for σd corresponds to the value of (COVy∙y) determined according to EPG 321.3.2 Design Values for Strata with Constant Properties and shall be established according to the provisions of EPG 321.3.2. Similarly, the value for σs corresponds to the value for (COVy∙y) determined according to EPG 321.3.6 Design Values from Surrogate Measurements and shall be established according to the provisions of EPG 321.3.6.
321.3.8 References
AASHTO (2009), AASHTO LRFD Bridge Design Specification: Customary U.S. Units, American Association of State Highway and Transportation Officials, Fourth Edition with 2008 and 2009 Interim Revisions.
Ang, A.H-S, and W.H. Tang (1975), Probability Concepts in Engineering Planning and Design, John Wiley and Sons, 409 pp.
Likos, W.J., L. Ge, D. Ding, S. Onyejekwe, M.D. Pierce, S.A. Grant, J.E. Loehr, and R.W. Stephenson (2011a), MoDOT Transportation Geotechnics Research Program: Laboratory Site Characterization Testing Program Data Report, Missouri Department of Transportation, OR11.XXX, XXX pp.
Likos, W.J., J.E. Loehr, N. Maerz, K.A. Magner, L. Ge, and R.W. Stephenson (2011b), MoDOT Transportation Geotechnics Research Program: Site Characterization Program Interpretation Report, Missouri Department of Transportation, OR11.XXX, XXX pp.
Loehr, J.E., A.Z. Boeckmann, P.L. Speckman, and D. Ding (2013), Procedures for Establishing Geotechnical Design Parameters from Two Data Sources, Final Project Report submitted to Missouri Department of Transportation, 22 pp..
Magner, K.A, N. Maerz, J.J. Bowders, M.D. Pierce, and J.E. Loehr (2011), MoDOT Transportation Geotechnics Research Program: Field Site Characterization Testing Program Data Report, Missouri Department of Transportation, OR11.XXX, XXX pp.
321.3.9 Commentary
These guidelines were developed based on a comprehensive research program conducted to improve design of bridge foundations and earth slopes. The methods provided in these provisions were established by combining theoretical considerations of parameter variability as well as empirical observations from a broad evaluation of site characterization techniques performed as a part of the research program. Additional details regarding the site characterization aspects of the research program can be found in Likos et al. (2011a), Magner et al. (2011), and Likos et al. (2011b).
The provisions of EPG 751.37 Drilled Shafts, EPG 751.38 Spread Footings and EPG 321.1 Design of Earth Slopes were developed under the presumption that parameter values and coefficients of variation are established according to the provisions of this article.
Commentary on EPG 321.3.1 General
Variability and uncertainty in design parameters depends on a number of factors that include the specific sampling and test method(s) utilized, the character of the specific site, and the quantity of sampling and testing performed. Variability and uncertainty also depends upon whether one is considering the variability of the measurements or the uncertainty in the actual or mean value of the parameter. The provisions of this article are intended for use in establishing the variability or uncertainty of the mean value of design parameters that are appropriate for use in EPG 751.37, EPG 751.38, and EPG 321.1.
Commentary on EPG 321.3.1.1 Relevant Design Parameters
Other design parameters may be required for specific EPG provisions. However, the parameters listed are those that require estimation of both the mean value and coefficient of variation for establishing resistance factor values.
Commentary on EPG 321.3.1.2 Development of Design Profiles for Relevant Design Properties
It is important to recognize that design profiles established according to the provisions of this article are not unique. Establishing design profiles for application of methods provided in EPG 751.37 Drilled Shafts, EPG 751.38 Spread Footings and EPG 321.1 Design of Earth Slopes necessarily involves judgment on the part of the designer because the type, quality, and quantity of testing performed for different sites will differ. Furthermore, two designers may rationally choose to represent the same set of data using different design profiles. Such differences are inherent to site characterization with limited data. The procedures provided in this article were developed with this realization in mind and the variabilities and uncertainties established following the provisions of this article reflect this fact.
In general, designers should seek to establish design profiles that have the least variability and uncertainty (i.e. the lowest COV) for the available data, because this will increase the efficiency of the specific design. However, designers must also consider the quality and quantity of available data, the criticality of the structure, and the potential cost implications of developing highly refined design profiles and balance these with the costs required to develop rational design profiles.
As shown in Figure 321.3.1.1 for Stratum I, Stratum IV, and Stratum V, the coefficient of variation of the mean value for a parameter is not strictly constant for strata deemed to have linearly varying parameter values. Within such strata, the coefficient of variation will tend to be smaller at depths where more measurements are available and larger at depths where fewer measurements are available (because the uncertainty is greater where fewer measurements are available). When measurements are evenly distributed throughout the stratum, the coefficient of variation will tend to be least near the middle of the stratum and greatest near the upper and lower boundaries of the stratum. Despite these predictable results, a constant coefficient of variation has been adopted in the relevant EPG provisions to simplify application of the provisions. Designers must therefore compute or select a reasonable average value of the coefficient of variation that generally reflects the variability and uncertainty in the mean value for the parameter of interest within the stratum.
Commentary on EPG 321.3.1.3 Minimum Testing Requirements
No minimum quantities for tests are required to use the provisions of EPG 751.37 Drilled Shafts, EPG 751.38 Spread Footings and EPG 321.1 Design of Earth Slopes. This is a significant departure from current AASHTO LRFD design specifications, which generally use constant resistance factors under the assumption that a minimum level of site characterization will be conducted. Instead, EPG 751.37, EPG 751.38 and EPG 321.1 provide resistance factors that depend upon the variability and uncertainty present in specific design parameters, which is directly influenced by the quantity of test measurements that are available. The intent of this approach is to guide development of appropriate site characterization activities through consideration of costs for additional characterization and cost savings that may be realized due to reductions in uncertainty, rather than requiring some minimum level of characterization. It is important to note that all resistance factors provided in EPG 751.37, EPG 751.38 and EPG 321.1 are intended to produce the target levels of reliability established by MoDOT, regardless of the level of uncertainty in design parameters. As such, increasing the number of test measurements will not measurably change the reliability of the final design. However, since greater resistance factors can be used when variability and uncertainty is reduced, increasing the quantity of site characterization will often result in more efficient and cost effective designs because it will allow for use of greater resistance factors. The role of the designer therefore is one of using judgment to optimize the level of site characterization based on the costs required for additional site characterization and the cost savings that may be realized from additional characterization.
Throughout these provisions, the variability and uncertainty in a design parameter is represented using the coefficient of variation (COV). For a specific site, the predominant means for reducing the coefficient of variation for a design parameter is by increasing the number of measurements of that parameter.
While the EPG provisions do not include minimum testing requirements, the provisions do require estimation of a value for the coefficient of variation in order to establish appropriate resistance factors. The provisions of EPG 321.3 require a minimum of three measurements of a parameter in order to quantitatively establish a value for the coefficient of variation. In cases where less than three measurements are available for a given stratum, designers must estimate values for the coefficient of variation based on experience and judgment. The coefficient of variation can be conservatively estimated to be equal to 1.0. However, experience will likely show that this is an excessively conservative value for most design cases. When estimating values for the coefficient of variation, designers should consider both the criticality of a structure and the sensitivity of the resulting designs to changes in the coefficient of variation. When in doubt, relatively large values for the coefficient of variation should be assumed.
Commentary on EPG 321.3.2 Design Values for Strata with Constant Properties
The provisions of this article are intended for use establishing design parameters for strata that are deemed to have properties that are practically uniform. At a given site, it is perfectly acceptable to establish one or more strata as having constant parameters and one or more different strata as having linearly varying parameters. In such cases, the provisions of this article shall be followed for strata having constant parameters and the provisions of EPG 321.3.3 Design Values for Strata with Linearly Varying Properties shall be followed for strata having linearly varying parameters.
Given a set of parameter measurements, calculation of the mean value and the coefficient of variation for a design parameter is relatively straightforward. However, it is not uncommon to encounter cases where some measurements may contain “outliers” that may not reflect the actual value of the relevant design parameter. Such outliers can arise when testing errors are made, or when the stratum of interest contains “lenses” or “stringers” of material that may not be representative of the collective stratum. The question then becomes whether to include outlier measurements in the calculation of the mean and/or coefficient of variation of the design parameter. As a general rule, measurements should be disregarded (i.e. “thrown out”) with great caution, and only after careful deliberation of whether the measured value is truly an outlier. This is especially true when relatively few measurements are available for the stratum. If the designer truly believes that a measurement is inaccurate, or not representative of the broader stratum, then the measurement should be disregarded. However, if there is any doubt about whether the measurement is valid, it should generally be included in the calculations to establish the mean value and coefficient of variation for the parameter. Measurements should never be disregarded simply for the purpose of skewing the mean value or reducing the computed coefficient of variation.
Commentary on EPG 321.3.2.1 Establishing Mean Values for Strata with Constant Property
No commentary.
Commentary on EPG 321.3.2.2 Establishing COV Values for Strata with Constant Property
These provisions are based on the assumption that the measurements are independent measurements (i.e. uncorrelated). While this assumption is seldom strictly satisfied, it is a practical and often conservative assumption to make.
Commentary on EPG 321.3.3 Design Values for Strata with Linearly Varying Properties
The provisions of this article are intended for use establishing design parameters for strata that are deemed to have properties that vary linearly with depth or elevation across the stratum. At a given site, it is perfectly acceptable to establish one or more strata as having constant parameters and one or more different strata as having linearly varying parameters. In such cases, the provisions of this article shall be followed for strata having linearly varying parameters and the provisions of EPG 321.3.2 shall be followed for strata having constant parameters.
Given a set of parameter measurements, calculation of the mean value and the coefficient of variation for a design parameter is relatively straightforward. However, it is not uncommon to encounter cases where some measurements may contain “outliers” that may not reflect the actual value of the relevant design parameter. Such outliers can arise when testing errors are made, or when the stratum of interest contains “lenses” or “stringers” of material that may not be representative of the collective stratum. The question then becomes whether to include outlier measurements in the calculation of the mean and/or coefficient of variation of the design parameter. As a general rule, measurements should be disregarded (i.e. “thrown out”) with great caution, and only after careful deliberation of whether the measured value is truly an outlier. This is especially true when relatively few measurements are available for the stratum. If the designer truly believes that a measurement is inaccurate, or not representative of the broader stratum, then the measurement should be excluded from calculation of the mean and coefficient of variation. However, if there is any doubt about whether the measurement is valid, it should generally be included in the calculations to establish the mean value and coefficient of variation for the parameter. Measurements should never be excluded simply for the purpose of skewing the mean value or reducing the computed coefficient of variation.
Commentary on EPG 321.3.3.1 Establishing Mean Values for Strata with Linearly Varying Property
It is anticipated that the least squares fitting function LINEST provided in Microsoft Excel© or other similar programs will most commonly be used to establish the linear fit to the available data. Additional guidance on the least squares fitting technique can be found in Ang and Tang (1975), or many other references on statistics.
Commentary on EPG 321.3.3.2 Establishing COV Values for Strata with Linearly Varying Property
The correlation coefficient, ρ, is the correlation coefficient of the regression coefficients, m and b, and not the correlation coefficient of the measured parameter with depth or elevation. Unfortunately, the Microsoft Excel© LINEST function does not provide the correlation coefficient, ρ, needed for estimation of the coefficient of variation of the mean value of the parameter. The correlation coefficient can, however, be calculated from the least squares fit to the data with additional calculations that are beyond the scope of this commentary. Designers are encouraged to consult any of a number of available references on statistics, such as Ang and Tang (1975), for additional guidance on calculation of the correlation coefficient of regression coefficients.
The assumption of a correlation coefficient, ρ, equal to 1.0 may be extremely conservative in some instances. Use of ρ = 1.0 may therefore be appropriate for establishing preliminary estimates for the coefficient of variation so that preliminary or initial trial designs can be determined. If such design are determined to be sensitive to the value of ρ, the additional analysis required to establish the coefficient of variation may be justified.
COVy is dependent on the depth z used for the calculations, both because σy is dependent upon z and because the mean value y is also dependent upon z. For design purposes, a single value of the coefficient of variation must be chosen to reflect the nominal coefficient of variation across the entire stratum. In general, the COV will tend to be smaller near depths or elevations where measurements are available and greater at depths/elevations where few measurements exist. The coefficient of variation should therefore be computed for several depths/elevations within the stratum, and a nominal value for COV chosen to reflect the general variability of the mean value of the measurements.
Commentary on EPG 321.3.4 Design Values for Mohr-Coulomb Shear Strength Parameters
Calculations required to establish design values for Mohr-Coulomb shear strength parameters, c and ϕ, are similar to those required to establish design values for parameters that vary linearly over the depth of a stratum. The notable difference in the calculations is that the linear fit is performed for data reflecting shear strength as a function of either total or effective stress, rather than for data reflect a design parameter as a function of depth or elevation.
The provisions of this article require that data reflecting the normal stress and shear stress on the failure plane at failure be established for all test measurements and that these data be used to establish a best fit failure envelope and coefficient of variation of the shear strength. These values are respectively denoted as σff and τff for the normal stress and shear stress on the failure plane at failure. Calculation of σff and τff from direct shear tests is generally straightforward as σff is taken to be the vertical normal stress on the specimen at failure (i.e. the normal load divided by the specimen area at failure) and τff is taken to be the shear stress on the horizontal plane at failure (i.e. the shear load divided by the specimen area at failure). Values for σff and τff can also be established from results of triaxial tests as follows:
| (consistent units) | Equation Commentary 321.3.4.1 | |
| (consistent units) | Equation Commentary 321.3.4.2 |
where
- σff = total normal stress on the failure plane at failure (consistent units of stress),
- τff = shear stress on the failure plane at failure (consistent units of stress),
- σ1f = total major principal stress at failure (consistent units of stress),
- σ3f = total minor principal stress at failure (consistent units of stress), and
- ϕ = Mohr-Coulomb angle of internal friction in terms of total stresses (degrees).
For effective stress analyses, values for and τff can be similarly established as:
| (consistent units) | Equation Commentary 321.3.4.3 | |
| (consistent units) | Equation Commentary 321.3.4.4 |
where
- = effective normal stress on the failure plane at failure (consistent units of stress),
- τff = shear stress on the failure plane at failure (consistent units of stress),
- = effective major principal stress at failure (consistent units of stress),
- = effective minor principal stress at failure (consistent units of stress), and
- = Mohr-Coulomb angle of internal friction in terms of effective stresses (degrees).
Calculation of the normal and shear stress on the failure plane at failure requires knowledge of the angle of internal friction (ϕ), in terms of either total or effective stresses. However, the value for ϕ or is not known until the best fit relationship is established so an iterative calculation is required wherein an estimate of the angle of internal friction is first assumed, from which trial values for σff and τff can be established. These trial values for σff and τff can then be used to determine a best fit failure envelope. The angle of internal friction from this envelope should be compared to the one originally assumed to calculate σff and τff. If the values are different, the calculations should be iteratively repeated until the assumed value of the friction angle is practically equal to the friction angle produced from the least squares best fit calculations.
Commentary on EPG 321.3.4.1 Establishing Mean Values for c and ϕ in Terms of Total Stresses
No commentary.
Commentary on EPG 321.3.4.2 Establishing Mean Values for and in Terms of Effective Stresses
No commentary.
Commentary on EPG 321.3.4.3 Establishing COV Values for Shear Strength from Mohr-Coulomb Shear Strength Parameters
The correlation coefficient, ρ, is the correlation coefficient of the regression coefficients, tanϕ and c or tan and , and not the correlation coefficient of the measured values of shear strength with total or effective normal stress. Unfortunately, the Microsoft Excel© LINEST function does not provide the correlation coefficient, ρ, needed for estimation of the coefficient of variation of the mean value of the parameter. The correlation coefficient can, however, be calculated from the least squares fit to the data with additional calculations that are beyond the scope of this commentary. Designers are encouraged to consult any of a number of available references on statistics, such as Ang and Tang (1975), for additional guidance on calculation of the correlation coefficient.
The assumption of a correlation coefficient, ρ, equal to 1.0 may be extremely conservative in some instances. Use of ρ = 1.0 may therefore be appropriate for establishing preliminary estimates for the coefficient of variation so that preliminary or initial trial designs can be determined. If such design are determined to be sensitive to the value of ρ, the additional analysis required to establish the coefficient of variation may be justified.
COVss is dependent on the total or effective normal stress, σ or , used for the calculations, both because σss is dependent upon σ or and because the mean value s is also dependent upon σ or . For design purposes, a single value of the coefficient of variation must be chosen to reflect the nominal coefficient of variation across the range in total or effective normal stresses for which the strength envelope will be used. In general, the COV will tend to be smaller at normal stresses where measurements are available and greater at normal stresses where few measurements exist. The coefficient of variation should therefore be computed for a range of normal stresses appropriate for the problem being considered, and a nominal value for COV chosen to reflect the general variability of the mean value of the measurements.
Commentary on EPG 321.3.5 Uncertainty Modifiers to Account for Quantity of Tests
The empirical modifier, ζ, in essence imposes a penalty to account for the fact that the variability and uncertainty derived from a set of measurements may underestimate the actual variability and uncertainty present at a site. Because underestimating the coefficient of variation will produce unconservative designs, the modifier is introduced to avoid the rare case where the coefficient of variation derived from a set of measurements may dramatically under-represent the actual variability and uncertainty that is present in the overall population. The likelihood of this occurring is greatest when there are few measurements and lessens dramatically with increasing numbers of measurements. The modifier is thus greatest for small numbers of measurements and decreases with increasing numbers of measurements.
The possibility also exists for obtaining an unrealistically large value for the coefficient of variation from a specific set of measurements. Such a result would produce a conservative design since it would produce a resistance factor that is generally less than what would be required if the actual population coefficient of variation were know. However, since it is not possible to know whether the coefficient of variation calculated from a specific set of measurements is accurate, conservative, or unconservative, prudence requires that the modifier be applied in all cases to avoid unconservative results that might produce performance problems.
The modifiers provided in EPG 321.3.5 are empirical in the sense that the modifier values were established from analyses of empirical measurements of relevant design parameters for several sites that are generally representative of conditions encountered by MoDOT for design of bridges and other structures (Likos et al., 2011b). The analyses performed consisted of a series of hypothetical sampling cases from extensive sets of measurements to evaluate the range of potential errors that may be introduced for different quantities of measurements. From these analyses, modifiers were established using judgment so that the likelihood of calculating an unrealistically low value for the coefficient of variation would be small. These analyses were performed using measurements of all design parameters utilized within EPG 751.37 Drilled Shafts, EPG 751.38 Spread Footings and EPG 321.1 Design of Earth Slopes. The modifiers provided in EPG 321.3.5 reflect a nominal fit to the collection of curves produced from these analyses so that a single modifier could be used for all design parameters. It is also possible to produce a series of modifiers, each reflecting the relationship for a different design parameter. However, this approach was not adopted in order to keep application of the empirical modifier as straightforward as possible.
Commentary on EPG 321.3.6 Design Values from Surrogate Measurements
The provisions of this article are derived from work described in Loehr et al. (2013). Common examples of surrogate measurements include use of Standard Penetration Test measurements or Cone Penetration Test Measurements to establish design parameters, which generally require application of an empirical relationship between the surrogate measurement and the design parameter of interest (e.g. SPT blow counts and uniaxial compressive strength). Such correlations introduce uncertainty into estimation of the mean and the coefficient of variation of the mean for a parameter, in addition to the variability and uncertainty in the measurements themselves, that must be accounted for in establishing appropriate design values for a parameter of interest.
The provisions of this article presume that there is a linear relationship between the surrogate measurement and the parameter of interest of the form:
| y = β0 + β1x | (consistent units) | Equation Commentary 321.3.6.1 |
where
- y = f(x) = value for parameter of interest (consistent units),
- x = value of the surrogate measurement (consistent units),
- β0 = y-intercept of linear relation between surrogate measurement and parameter of interest (consistent units), and
- β1 = slope of linear relation between surrogate measurement and parameter of interest (consistent units).
Such linear relations are common. In cases where the relationship between a surrogate measurement and the parameter of interest is non-linear, similar methods can be applied for transformed values of the surrogate and/or parameter of interest that serve to “linearize” the relationship as described in Loehr et al (2013).
The methods described in Loehr et al. (2013) can be applied to a wide range of geotechnical design parameters and to different surrogate measurements. At present, specific equations have only been developed for establishing design values for the uniaxial compressive strength (q_u) of shale from SPT measurements (N_eq). It is anticipated that additional provisions will be developed in the future for other design parameters and other surrogate measurements.
Commentary on EPG 321.3.6.1 Establishing Mean Value of qu from Standard Penetration Tests in Shale
The provisions of this article were derived from the work described in Loehr et al. (2013), using results from regression performed using a natural logarithm transformation of both the direct (qu) and surrogate (Neq) measurements. While such transformations complicate the equations slightly, use of untransformed measurements produces an equation with such great variability and uncertainty that SPT measurements are rendered practically useless. The additional complication introduced by the logarithmic transformation is therefore necessary if some value is to be derived from use of SPT measurements for establishing design values for qu.
It is important to emphasize that the mean of the natural logarithm of a set of numbers is not the same as the natural logarithm of the mean of the same set of numbers. Thus, when applying the provisions of this article, the natural logarithm of the individual Neq measurements must be taken prior to computing the mean of the log transformed values. It is not acceptable to take the natural logarithm of the mean of the Neq measurements.
Commentary on EPG 321.3.6.2 Establishing COV Values for qu from Standard Penetration Tests in Shale
The provisions of this article were derived from the work described in Loehr et al. (2013), using results from regression performed using a natural logarithm transformation of both the direct (qu) and surrogate (Neq) measurements. While such transformations complicate the equations slightly, use of untransformed measurements produces an equation with such great variability and uncertainty that SPT measurements are rendered practically useless. The additional complication introduced by the logarithmic transformation is therefore necessary if some value is to be derived from use of SPT measurements for establishing design values for qu.
It is important to emphasize that the mean of the natural logarithm of a set of numbers is not the same as the natural logarithm of the mean of the same set of numbers. Thus, when applying the provisions of this article, the natural logarithm of the individual Neq measurements must be taken prior to computing the mean of the log transformed values. It is not acceptable to take the natural logarithm of the mean of the Neq measurements.
Commentary on EPG 321.3.7 Design Values from Combined Direct and Surrogate Measurements
The provisions of this article were established from the work described in Loehr et al. (2013). These provisions can be applied to a number of different design parameters where both direct and surrogate measurements are available.


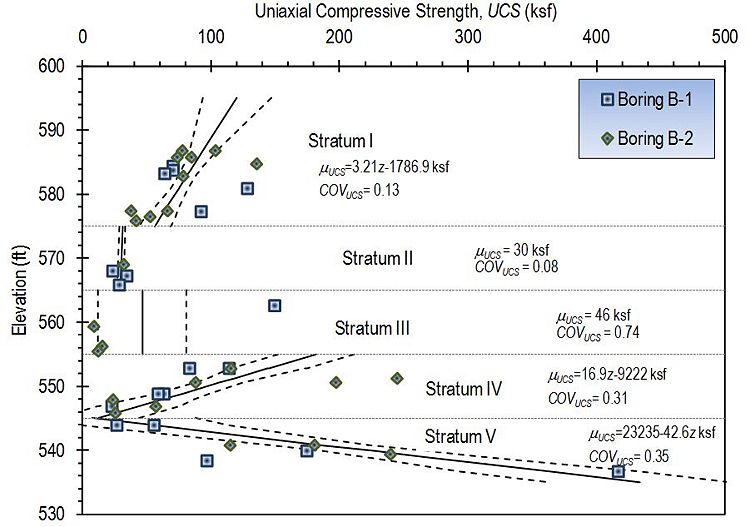






















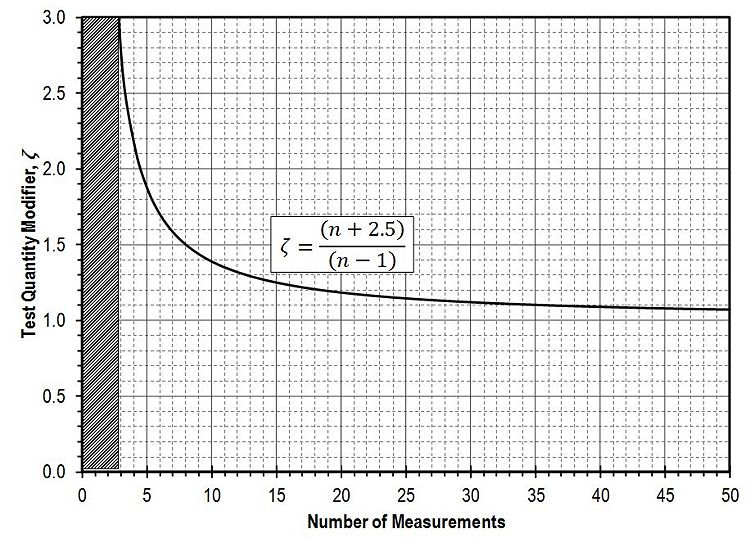


![{\displaystyle COV_{q_{u}}={\frac {\zeta \sigma _{q_{u}}}{q_{u}}}={\frac {\zeta {\sqrt {{q_{u}}^{2}{\Bigg [}1.654+1.882{\frac {\sigma _{ln({\hat {N}}_{eq})}^{2}}{n_{s}}}-0.503\cdot {\overline {ln(N_{eq})}}+0.049\cdot {\overline {ln(N_{eq})}}^{2}{\Bigg ]}}}}{q_{u}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed10273935b97b703b8e04b56b4e279be3628056)
![{\displaystyle {\sqrt {{q_{u}}^{2}{\Bigg [}1.654+1.882{\frac {\sigma _{ln({\hat {N}}_{eq})}^{2}}{n_{s}}}-0.503\cdot {\overline {ln(N_{eq})}}+0.049\cdot {\overline {ln(N_{eq})}}^{2}{\Bigg ]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b262b7894dc1e688cbafbbe05fd2126150445eb8)


















