750.3 Bridges
Contents
750.3.1 Hydraulic Considerations for Bridge Layout
750.3.1.1 Abutment Layout
Abutments shall be placed such that spill fill slopes do not infringe upon the channel; the toes of the spill fill slopes may be no closer to the center of the channel than the toe of the channel banks. The Soil Survey provided by the Materials Division gives minimum spill fill slopes based on slope stability criteria. The minimum bridge length for stability criteria is thus determined by projecting the stability slopes outward from the toes of the channel slopes as shown below. For structures crossing an NFIP regulatory floodway, abutments shall be placed such that the toes of the spill fill slopes are outside the floodway limits.

750.3.1.2 Pier/Bent Layout
Piers should not be placed in the channel except where absolutely necessary. Where possible, piers are to be placed no closer to the center of channel than the toe of the channel banks. When the proposed bridge length is such that piers in the channel are necessary, the number of piers in the channel shall be kept to a minimum (See Abutment and Pier Location Limits above).
Bents shall be skewed where necessary to align piers to the flow direction, at the design discharge, to minimize the disruption of flow and to minimize scour at piers. For stream crossings, skew angles less than 10 degrees are not typically used, and skew angles should be evenly divisible by 5 degrees.
750.3.1.3 Roadway Fill Removal
When replacing an existing bridge, the bridge memorandum and design layout should note whether the existing roadway fill is to be removed. Normally, the designer should specify that the existing fill is to be removed to the natural ground line to the limits of the design high water.
750.3.1.4 Velocity
Average velocity through the structure and average velocity in the channel shall be evaluated to insure they will not result in damage to the highway facility or an increase in damage to adjacent properties. Average velocity through the structure is determined by dividing the total discharge by the total area below design high water. Average velocity in the channel is determined by dividing the discharge in the channel by the area in the channel below design high water.
Acceptable velocities will depend on several factors, including the "natural" or "existing" velocity in the stream, existing site conditions, soil types, and past flooding history. Engineering judgment must be exercised to determine acceptable velocities through the structure.
Past practice has shown that bridges meeting backwater criteria will generally result in an average velocity through the structure of somewhere near 6 ft/s. An average velocity significantly different from 6 ft/s may indicate a need to further refine the hydraulic design of the structure.
750.3.1.5 Hydraulic Performance Curve
The hydraulic performance of the proposed structure shall be evaluated at various discharges, including the 10-, 50-, 100-, and 500-year discharges. The risk of significant damage to adjacent properties by the resulting velocity and backwater for each of these discharges shall be evaluated.
750.3.1.6 Flow Distribution
Flow distribution refers to the relative proportions of flow on each overbank and in the channel. The existing flow distribution should be maintained whenever possible. Maintaining the existing flow distribution will eliminate problems associated with transferring flow from one side of the stream to the other, such as significant increases in velocity on one overbank. One-dimensional water surface profile models are not intended to be used in situations where the flow distribution is significantly altered through a structure. Maintaining the existing flow distribution generally results in the most hydraulically efficient structure.
750.3.1.7 Bank/Channel Stability
Bank and channel stability must be considered during the design process. HEC-20 provides additional information on factors affecting streambank and channel stability, and provides procedures for analysis of streambank and channel stability. At a minimum, a qualitative analysis (HEC-20 Level 1) of stream stability shall be performed. If this qualitative analysis indicates a high potential for instability at the site, a more detailed analysis may be warranted. See the AASHTO Highway Drainage Guidelines Volume VI and HEC-20 for additional information.
750.3.1.8 Scour
Hydraulic analysis of a bridge design requires evaluation of the proposed bridge's vulnerability to potential scour. Unanticipated scour at bridge piers or abutments can result in rapid bridge collapse and extreme hazard and economic hardship.
Bridge scour is composed of several separate yet interrelated components, including long term profile changes, contraction scour and local scour. Total scour depths are obtained by adding all of these components together for a 500 yr. design frequency.
Lateral channel movement must also be considered in design of bridge foundations. Stream channels typically are not fixed in location and tend to move laterally. Consideration should be given to setting foundation elevations on the overbanks at the same elevation as foundations in the channel when significant lateral channel migration is expected.
The bottom of pile footing elevations should be set at or below the calculated total scour depth, provided the calculated depths appear reasonable. A minimum bottom of footing elevation of 9.0 ft below the existing ground or channel bottom shall be used. The bottom of footing elevation shall remain the same whether a seal course is used or not; do not adjust the bottom of footing if a seal course is used. Considerable exercise of engineering judgement may be required in setting these footing depths.
Refer to HEC-18 when setting bottom of spread footing elevations.

750.3.1.9 List of References
1. Stream Stability at Highway Structures, Federal Highway Administration Publication FHWA-IP-90-014 - Hydraulic Engineering Circular No. 20, November 1995
2. AASHTO Highway Drainage Guidelines, American Association of State Highway and Transportation Officials, 1992
3. Guidelines for Determining Flood Flow Frequency, United States Water Resources Council, Bulletin #17B of the Hydrology Committee, September 1981
4. Technique for Estimating the 2- to 500-Year Flood Discharges on Unregulated Streams in Rural Missouri, Alexander and Wilson, USGS Water-Resources Investigations Report 95-4231, 1995
5. Techniques for Estimating Flood-Peak Discharges for Urban Basins in Missouri, Becker, USGS Water-Resources Investigations Report 86-4322, 1986
6. HEC-RAS User Manual, US Army Corps of Engineers, April 1997
7. HEC-RAS Hydraulic Reference Manual, US Army Corps of Engineers, April 1997
8. HEC-RAS Applications Guide, US Army Corps of Engineers, April 1997
9. Roughness Characteristics of Natural Channels, Barnes, USGS Water-Supply Paper 1849, 1977
10. Guide for Selecting Manning's Roughness Coefficients for Natural Channels and Floodplains, Federal Highway Administration, Report No. FHWA-TS-84-204, April 1984
11. Open-Channel Hydraulics, Ven Te Chow, McGraw Hill Book Company, 1988, pp. 108-123
12. Hydraulic Design Series No. 5 - Hydraulic Design of Highway Culverts, Federal Highway Administration, Report No. FHWA-IP-85-15, September 1985
13. Evaluating Scour at Bridges, Federal Highway Administration Publication FHWA-IP-90-017 - Hydraulic Engineering Circular No. 18, November 1995
14. The Design of Encroachments on Flood Plains Using Risk Analysis, Federal Highway Administration - Hydraulic Engineering Circular No. 17, April 1981
750.3.2 Hydraulic Design Process
750.3.2.1 Overview
The hydraulic design process begins with the collection of data necessary to determine the hydrologic and hydraulic characteristics of the site. The hydraulic design process then proceeds through the hydrologic analysis stage, which provides estimates of peak flood discharges through the structure. The hydraulic analysis provides estimates of the water surface elevations required to pass those peak flood discharges. A scour analysis provides an estimate of the required depth of bridge foundations. A risk assessment is performed for all structures, and when risks to people, risks to property, or economic impacts are deemed significant, a least total economic cost analysis shall be performed to insure the most appropriate and effective expenditure of public funds. Finally, proper documentation of the hydraulic design process is required.
The level of detail of the hydrologic and hydraulic analyses shall remain consistent with the site importance and with the risk posed to the highway facility and adjacent properties by flooding.
750.3.2.2 Data Collection
The first step in hydraulic design is collecting all available data pertinent to the structure under consideration. Valuable sources of data include the bridge survey; aerial photography and various maps; site inspections; soil surveys; plans, surveys, and computations for existing structures; and flood insurance study data.
750.3.2.2.1 Bridge Survey
The bridge survey is prepared by district personnel and provides information regarding existing structures, nearby structures on the same stream, and streambed and valley characteristics including valley cross-sections along the centerline of the proposed structure, valley cross-sections upstream and downstream of the proposed structure, and a streambed profile through the proposed structure.
Location of the surveyed valley cross-sections is an important factor in developing the best possible water surface profile model for the proposed structure. For this reason, inclusion of the bridge survey as an agenda item on an initial core team meeting to discuss appropriate location of the valley cross-sections is recommended.
Bridge surveys are conducted in accordance with Bridge Reports and Layouts.
750.3.2.2.2 Photographs and Maps
Aerial photography, USGS topographic maps, and county maps should be consulted to determine the geographic layout of the site. Aerial photographs, in particular, can provide information on adjacent properties that may be subjected to increased risk of flood damage by the proposed structure, and may be available from the MoDOT photogrammetric section.
750.3.2.2.3 Site Inspection
A site inspection is a vital component of the hydrologic and hydraulic analyses, and is especially important for those sites subjected to risk of significant flood damage. A visit to the proposed site will provide the following information:
- selection of roughness coefficients
- evaluation of overall flow directions
- observation of land use and related flood hazards
- geomorphic observations (bank and channel stability)
- high-water marks
- evidence of drift and debris
- interviews with local residents or construction and maintenance engineers on flood history
Photographs taken during the site visit provide documentation of existing conditions and will aid in later determination of hydraulic characteristics.
750.3.2.2.4 Flood Insurance Study Data
If a Flood Insurance Study (FIS) has been performed for the community in which the structure is proposed, the FIS may provide an additional data source. The FIS may contain information on peak flood discharges, water surface profile elevations, and information on regulatory floodways.
750.3.2.2.5 Data Review
After all available data have been compiled, the data should be reviewed for accuracy and reliability. Special attention should be given to explaining or eliminating incomplete, inconsistent or anomalous data.
750.3.2.3 Bridge Hydrologic Analysis
Peak flood discharges are determined by one of the following methods. If the necessary data is available, discharges should be determined by all methods and engineering judgment used to determine the most appropriate.
750.3.2.3.1 Historical USGS Stream Gage Data
See Historical USGS Stream Gage Data
750.3.2.3.2 NFIP Flood Insurance Study Discharges
See NFIP Flood Insurance Study Discharges
750.3.2.3.3 USGS Rural Regression Equations
See Rural Regression Equations.
750.3.2.3.4 USGS Urban Regression Equations
See Urban Regression Equations.
750.3.2.3.5 Other Methods
Other methods of determining peak flood discharges include the Corps of Engineers' HEC-1 and HEC-HMS hydrologic modeling software programs, the SCS TR-20 hydrologic modeling software program, and the SCS TR-55 Urban Hydrology for Small Watersheds method. See also Flood Hydrographs.
Use of these alternate methods should be limited to situations where the methods given above are deemed inappropriate or inadequate.
750.3.2.4 Hydraulic Analysis of Bridges
The Corps of Engineers Hydrologic Engineering Center's River Analysis System (HEC-RAS) shall be used to develop water surface profile models for the hydraulic analysis of bridges. Documentation on the use of HEC-RAS is available in references (6), (7), and (8).
Hydraulic design of bridges requires analysis of both the "natural conditions" and the "proposed conditions" at the site. In order to show that structures crossing a NFIP regulatory floodway cause no increase in water surface elevations, it is also necessary to analyze the "existing conditions."
For these reasons, water surface profile models for bridges shall be developed for three conditions:
- Natural conditions - Includes natural channel and floodplain, including all modifications made by others, but without MoDOT structures
- Existing conditions - Includes natural conditions and existing MoDOT structure(s)
- Proposed conditions - Includes natural conditions, existing MoDOT structures if they are to remain in place, and proposed MoDOT structure(s)
Backwater is determined by comparing the water surface elevations upstream of the structure for either existing conditions or proposed conditions to the corresponding water surface elevation for the natural conditions.
For bridges near a confluence with a larger stream downstream of the site, additional models may be required. The water surface profile and resulting backwater should be evaluated both with and without backwater from the larger stream. The higher backwater resulting from the proposed structure shall be considered to control.
The hydraulic model in HEC-RAS is based on an assumption of one-dimensional flow. If site conditions impose highly two-dimensional flow characteristics (i.e. a major bend in the stream just upstream or downstream of the bridge, very wide floodplains constricted through a small bridge opening, etc.), the adequacy of these models should be considered. A two-dimensional model may be necessary in extreme situations.
750.3.2.4.1 Design High Water Surface Elevation
The design high water surface elevation is the normal water surface elevation at the centerline of the roadway for the design flood discharge. This elevation may be obtained using the slope-area method or from a "natural conditions" water surface profile.
750.3.2.4.2 Slope-Area Method
The slope-area method applies Manning's equation to a natural valley cross-section to determine stage for a given discharge. Manning's equation is given as:
- where:
- Q = Discharge (cfs)
- n = Manning's roughness coefficient
- A = Cross-sectional area (ft2)
- R = Hydraulic radius = A/P
- P = Wetted perimeter (ft)
- So = Hydraulic gradient (ft/ft)
In order to apply Manning's equation to a natural cross-section, the cross-section must be divided into sub-sections. The cross-section should be divided at abrupt changes in geometry and at changes in roughness characteristics.
For a given water surface elevation, the discharge can be determined directly from Manning's equation. Determination of the water surface elevation for a given discharge requires an iterative procedure.
The slope-area method should not be used with the roadway centerline valley cross-section to determine the design high water surface elevation when the centerline cross-section is not representative of the stream reach, such as when the new alignment follows or is very near the existing alignment. The centerline cross-section should also not be used when the centerline cross-section is not taken perpendicular to the direction of flow, such as when the alignment is skewed to the direction of flow or is on a horizontal curve. In these cases, an upstream or downstream valley cross-section should be used to determine the design high water surface elevation. The water surface elevation for an upstream or downstream valley cross-section can be translated to the roadway centerline by subtracting or adding, respectively, the hydraulic gradient multiplied by the distance along the stream channel from the valley cross-section to the roadway centerline.
A computer program is available to assist in making the slope-area calculations.
750.3.2.4.3 Roughness Coefficients
Roughness coefficients (Manning's "n") are selected by careful observation of the stream and floodplain characteristics. Proper selection of roughness coefficients is very significant to the accuracy of computed water surface profiles. The roughness coefficient depends on a number of factors including surface roughness, vegetation, channel irregularity, and depth of flow. It should be noted that the discharge in Manning's equation is inversely proportional to the roughness coefficient; a 10% decrease in roughness coefficient will result in a 10% increase in the discharge for a given water surface elevation.
It is extremely important that roughness coefficients in overbank areas be carefully selected to represent the effective flow in those areas. There is a general tendency to overestimate the amount of flow occurring in overbank areas, particularly in broad, flat floodplains. Increasing the roughness coefficients on overbanks will increase the proportion of flow in the channel, with a corresponding decrease in the proportion of flow on the overbanks.
References (9), (10), and (11) provide guidance on the selection of roughness coefficients.
750.3.2.4.4 Hydraulic Gradient (Streambed Slope)
The hydraulic gradient, So, is the slope of the water surface in the vicinity of the structure. It is generally assumed equal to the slope of the streambed in the vicinity of the structure. Note that the hydraulic gradient is typically much smaller than the valley slope used in the USGS regression equations. Hydraulic gradient is a localized slope, while valley slope is the average slope of the entire drainage basin.
Hydraulic gradient is determined by one of two methods, depending on drainage area:
- For drainage areas less than 10 mi2, the gradient is determined by fitting a slope to the streambed profile given on the bridge survey.
- For drainage areas greater than 10 mi2, the gradient is determined from USGS 7.5 minute topographic maps by measuring the distance along the stream between the nearest upstream and downstream contour crossings of the stream. The hydraulic gradient is then given by the vertical distance between contours divided by the distance along the stream between contours. Dividers set to 0.1 mi should be used to measure the distance along the stream.
750.3.2.4.5 Overtopping Discharge and Frequency
The overtopping flood frequency of the stream crossing system - roadway and bridge - shall be determined if the overtopping frequency is less than 500-years. An approximate method of determining the overtopping discharge uses the slope-area method given above and setting the stage to the elevation of the lowest point in the roadway. A more accurate method involves using a trial-and-error procedure, adjusting the discharge in the HEC-RAS proposed conditions model until flow just begins to overtop the roadway. The overtopping frequency can then be estimated by linear interpolation from previously developed discharge-frequency data.
750.3.2.4.6 Waterway Enlargement
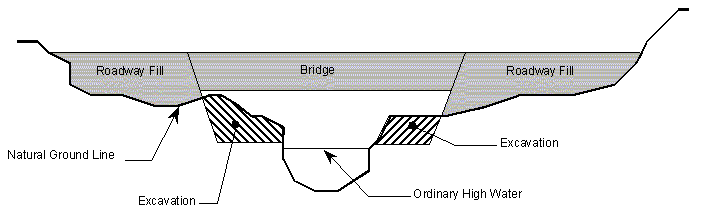
There are situations where roadway and structural constraints dictate the vertical positioning of a bridge and result in small vertical clearances between the low chord and the ground. In these cases, significant increases in span length provide small increases in effective waterway opening. It is possible to improve the effective waterway area by excavating a flood channel through the reach affecting the hydraulic performance of the bridge. This is accomplished by excavating material from the overbanks as shown in the figure Typical Excavation for a Flood Channel below; enlargement of the channel itself is avoided where possible as excavation below ordinary high water is subject to 404 permit requirements.
A similar action may be taken to compensate for increases in water surface elevations caused by bridge piers in a floodway.
There are, however, several factors that must be accommodated when this action is taken.
- The flow line of the flood channel must be set above the ordinary high water elevation.
- The flood channel must extend far enough upstream and downstream of the bridge to establish the desired flow regime through the affected reach.
- Stabilization of the flood channel to prevent erosion and scour should be considered.
750.3.2.5 Scour Analysis
Current methods of analyzing scour depths are based mainly on laboratory experiment rather than on practical field data. The results should be carefully reviewed and engineering judgment used to determine their applicability to actual field conditions.
HEC-RAS includes the ability to calculate scour depths. The methods used to calculate those depths are based on the FHWA HEC-18 publication, and are presented below for convenience.
750.3.2.5.1 Long Term Profile Changes - Aggradation and Degradation
Long term profile changes result from aggradation or degradation in the stream reach over time. Aggradation involves the deposition of sediment eroded from the channel and banks upstream of the site. Degradation involves the lowering or scouring of a streambed as material is removed from the streambed and is due to a deficit in sediment supply upstream. Aggradation and degradation are generally the result of changes in the energy gradient of the stream.
Aggradation and degradation over the life of a structure are difficult to predict. These long term profile changes are typically the result of human activities within the watershed including dams and reservoirs, changes in land use, gravel mining and other operations. HEC-18 and HEC-20 provide more information on predicting long term profile changes. Comparison of channel bottom elevations shown on plans for existing bridges to current survey data may be informative.
750.3.2.5.2 Contraction Scour
Contraction scour is generally caused by a reduction in flow area, such as encroachment on the floodplain by highway approaches at a bridge. Increased velocities and increased shear stress in the contracted reach result in transport of bed material. Contraction scour typically occurs during the rising stage of a flood event; as the flood recedes, bed material may be deposited back into the scour hole, leaving no evidence of the ultimate scour depth.
Contraction scour may be one of two types: live-bed contraction scour or clear water contraction scour. Live-bed scour occurs when the stream is transporting bed material into the contracted section from the reach just upstream of the contraction. Clear-water scour occurs when the stream is not transporting bed material into the contracted section. The type of contraction scour is determined by comparing the average velocity of flow in the channel or overbank area upstream of the bridge opening to the critical velocity for beginning of motion of bed material, Vc. The critical velocity can be determined using the following equation:
- where:
- C = Constant = 10.95
- Vc = Critical velocity above which bed material will be transported, ft/s
- D50 = Median diameter of bed material, ft.
- Y1 = Depth of flow in upstream channel or overbank, ft.
Calculated contraction scour depths greater than 6.0 ft should be viewed with some skepticism. Existing field data show that contraction scour depths greater than 6.0 ft are rarely encountered.
Live-Bed Contraction Scour - Live-bed contraction scour depths can be determined using the following equations:
- where:
- ys = Scour depth, ft.
- y1 = Average depth in upstream main channel, ft.
- y2 = Average depth in contracted section after scour, ft.
- y0 = Existing depth in contracted section before scour, ft.
- Q1 = Flow in upstream channel transporting sediment, ft3/s
- Q2 = Flow in contracted channel, ft3/s
- W1 = Bottom width of upstream main channel, ft.
- W2 = Bottom width of main channel in contracted section, ft.
- n1 = Manning's roughness coefficient for upstream main channel
- n2 = Manning's roughness coefficient for contracted channel
- k1 = Exponent depending on mode of bed material transport
The value of k1 can be obtained from the following table:
| V*/ω | K1 | Mode of Bed Material Transport |
|---|---|---|
| <0.50 | 0.59 | Mostly contract bed material discharge |
| 0.50 to 2.0 | 0.64 | Some suspended bed material discharge |
| >2.0 | 0.69 | Mostly suspended bed material discharge |
- where:
- V* = shear velocity in upstream section, ft/s
- ω = Median fall velocity of bed material based on D50, ft/s
- g = Acceleration due to gravity = 32.2 ft/s2
- S1 = Slope of energy grade line of main channel, ft/ft
- D50 = Median diameter of bed material, ft.
The fall velocity of bed material, ω, can be obtained from Figure 3 in HEC-18.
The upstream cross-section is typically located either one bridge opening length or the average length of constriction upstream of the bridge. This is consistent with the required location of the approach cross-section in both HEC-RAS and WSPRO.
Clear Water Contraction Scour - Clear-water contraction scour depths can be determined using the following equations:
- where:
- C = constant = 120
- ys = Scour depth, ft.
- y2 = Average depth in contracted section after scour, ft.
- y0 = Existing depth in contracted section before scour, ft.
- Q2 = Flow in contracted channel, ft3/s
- W2 = Bottom width of main channel in contracted section, ft.
- Dm = Diameter of smallest nontransportable particle in bed material in the contracted section, assumed equal to 1.25 D50, ft.
- D50 = Median diameter of bed material, ft.
750.3.2.5.3 Local Scour
Local scour involves removal of material from around piers, abutments and embankments and is caused by increased velocities and vortices induced by the obstruction to flow. As with contraction scour, bed material may be deposited back into the scour holes as floodwaters recede.
Pier scour and abutment scour are considered two distinct types of local scour.
Pier Scour - Pier scour depths can be determined using the following equation developed at CSU:
- where:
- y2 = Scour depth, ft.
- y1 = Flow depth directly upstream of pier, ft.
- K1 = Correction factor for pier nose shape
- K2 = Correction factor for angle of attack of flow
- K3 = Correction factor for bed condition
- K4 = Correction factor for armoring of bed material
- a = Pier width, ft.
- Fr1 = Froude number directly upstream of pier =
- V1 = Mean velocity of flow directly upstream of pier, ft/s
- g = Acceleration due to gravity = 32.2 ft/s2
The pier scour depth is limited to a maximum of 2.4 times the pier width for Froude numbers less than or equal to 0.8, and a maximum of 3.0 times the pier width for Froude numbers greater than 0.8.
For angles of attack less than 5 degrees, the value of K1 can be obtained from the tabale below. For angles greater than 5 degrees, the correction factor for angle of attack dominates and K1 should be set to 1.0.
| Shape of Pier Nose | K1 |
|---|---|
| Square Nose | 1.1 |
| Round Nose | 1 |
| Circular Cylinder | 1 |
| Group of Cylinders | 1 |
| Sharp Nose | 0.9 |
The correction factor for angle of attack of the flow, K2, can be determined using the following equation:
- where:
- K<sub2 = Correction factor for angle of attack of flow
- q = Angle of attack of the flow with respect to the pier
- L = Length of pier, ft.
- a = Pier width, ft.
The maximum value of L/a to be used in this equation is 12.
The correction factor for bed condition, K3, can be obtained from the following table:
| Bed Condition | Dune Height (ft.) | K3 |
|---|---|---|
| Clear-Water Scour | n/a | 1.1 |
| Plane Bed and Antidune Flow | n/a | 1.1 |
| Small Dunes | 12>H≥2 | 1.1 |
| Medium Dunes | 30>H≥10 | 1.2 to 1.1 |
| Large Dunes | H≥30 | 1.3 |
The correction factor for armoring, K4, can be determined using the following equations:
- where:
- VR = Velocity ratio
- V1 = Approach velocity, ft/s
- Vi = Approach velocity at which particles begin to move, ft/s
- Vc90 = Critical velocity for D90 bed material size, ft/s
- Vc50 = Critical velocity for D50 bed material size, ft/s
- a = Pier width, ft.
- C = constant = 10.95
- y = depth of water just upstream of pier, ft.
- Dc = Critical particle size for the critical velocity Vc, ft.
The minimum median bed material size, D50, for computing K4 is 0.2 ft. The minimum value of K4 is 0.7. VR must be greater than or equal to 1.0.
The pier width used in the above equations is that projected normal to the direction of flow. Piers should be skewed to minimize this width. The effect of debris should be considered in evaluating pier scour by considering the width of accumulated debris in determining the pier width used in the above equations.
For multiple columns with a spacing of 5 diameters or more, the total pier scour is limited to a maximum of 1.2 times the scour depth calculated for a single column. For multiple columns spaced less than 5 diameters apart, a "composite" pier width that is the total projected width normal to the angle of attack of flow should be used. For example, for three 6 ft piers spaced at 30 ft. apart, the pier width is somewhere between 6 ft. and 18 ft. (three times six feet), depending on the angle of attack.
Top width of pier scour holes, measured from the pier to the outer edge of the scour hole, can be estimated as 2.0 × ys.
Abutment Scour - Two equations are available for determining scour at abutments. The first equation, by Froelich, is given as:
- where:
- ys = Scour depth, ft.
- K1 = Coefficient for abutment shape
- K2 = Coefficient for angle of embankment to flow = (θ/90)0.13
- θ = Angle between embankment and flow (degrees), θ > 90 if embankment points upstream
- L' = Length of embankment projected normal to flow, ft.
- ya = Average depth of flow on the floodplain, ft.
- Fr = Froude number of approach flow upstream of abutment
- =
- Ve = Qe/Ae, ft/s
- Qe = flow obstructed by abutment and approach embankment, ft3/s
The second equation, from the FHWA publication Highways in the River Environment (HIRE), is recommended when the ratio of projected abutment length, L', to flow depth, ya, is greater than 25. This equation is given as:
- where:
- ys = Scour depth, ft.
- y1 = Flow depth at the abutment, ft.
- K1 = Coefficient for abutment shape
- K2 = Coefficient for angle of embankment
- Fr = Froude number of approach flow upstream of abutment
The value of K1 in both of the above equations can be obtained from the following table:
| Abutment Shape | K1 |
|---|---|
| Vertical-Wall Abutment | 1 |
| Vertical-Wall Abutment with Wing Walls | 0.82 |
| Spill-Through Abutment | 0.55 |
The value of K2 in the HIRE equation can be obtained from Figure 16 in HEC-18.
750.3.2.5.4 Total Scour
All the above types of scour are considered in determining proper depth of bridge foundations. The total scour is obtained by adding the individual scour components.
Provide justification if scour analysis is not performed (slope protection can eliminate the need for abutment scour calculations, etc.)




![{\displaystyle y_{2}=\left[{\frac {Q_{2}^{2}}{CD_{m}^{\frac {2}{3}}W_{2}^{2}}}\right]^{\frac {3}{7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8ffd7825f2292c2deb8ddcaa59e394e47be2bab)



![{\displaystyle K_{4}=\left[1-0.89(1-V_{R})^{2}\right]^{0.5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6df2e5fd4163cd538f95a9eae382ca8773fe0e)
![{\displaystyle V_{R}=\left[{\frac {V_{1}-V_{i}}{V_{c90}-V_{i}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdc46e3cb83a4e84bf5345bcbbb1b377a8ac0ec1)
![{\displaystyle V_{i}=0.645\left[{\frac {D_{50}}{a}}\right]^{0.053}V_{c50}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f519238e167bda20d53f46162cab28a40be3ba8)



