751.23 Prestressed Concrete Double Tee Girders
Contents
751.23.1 General
751.23.1.1 Material Properties
| Concrete | ||
|---|---|---|
| Standard compressive strength for P/S Double Tee Girder shall be: | ||
| Optional concrete strength shall be: | ||
| Modulus of Elasticity, | ||
| Where, | ||
| f'c in ksi | ||
| K1 = correction factor for source of aggregate aa = 1.0 unless determined by physical testing | ||
| Prestressing strand | ||
| Type of strand: | ||
| AASHTO M203 (ASTM A416) Grade 270 | ||
| Uncoated, seven-wire, low-relaxation strand | ||
| Ultimate tensile strength, | ||
| Yield strength, | ||
| Strand modulus of elasticity, | ||
| For standard concrete: | ||
| Strand diameter, | ||
| Strand area, | ||
| For optional concrete: | ||
| Strand diameter, | ||
| Strand area, | ||
| Maximum allowed initial prestress force (immediately prior to transfer) = fpbt = 0.75fpu kips LRFD table 5.9.3-1 | ||
| Maximum allowed initial prestress force per strand = Apsxfpbt kips | ||
| Maximum allowed initial force = 30.98 kips for 0.5 inch diameter strand 43.94 kips for 0.6 inch diameter strand | ||
| Total initial prestress force = (# of strands) x (required* initial prestress force per strand) | ||
| * Typically the required prestress force per strand is the maximum allowed prestress force. | ||
| Note: Report on the girder plans the required number of strands by design and the total initial prestress force using EPG 751.50 Standard Detailing Notes H2c1.3. | ||
| Mild reinforcing steel | ||
| Minimum yield strength, | ||
| Steel modulus of elasticity, | ||
751.23.1.2 Girder and Slab Design
The cast-in-place slab is designed to carry only the live load of the bridge. One layer of steel is used in each direction of the cast-in-place slab with 1" clearance from bottom of slab. A 1" integral wearing surface is deducted from effective slab depth for design.
The double tee girder flange is designed to carry the load of the cast-in-place slab, the flange weight and a 50 lb./sq. ft. construction dead load. (or a 300 lb. concentrated construction load per OSHA).
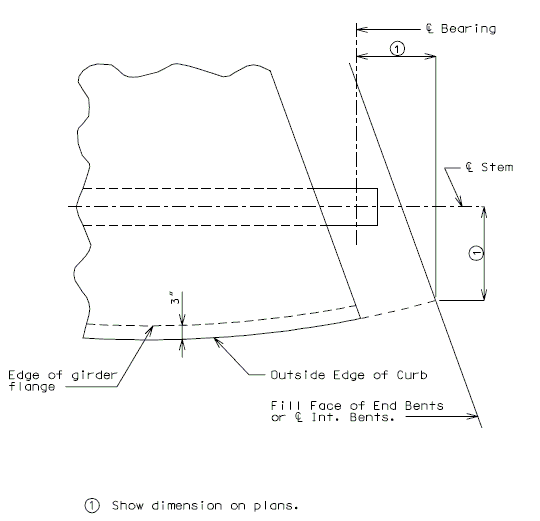
When determining the section properties of the double tee girder the center of gravity is based upon the total area (excluding corner fillets) of the entire exterior or interior girder and not on the individual stems. Moment of inertia and dead loads to each stem are figured to the center of the flange between the stems. The non-composite dead load of the external double tee girder is divided according to the following sketch.
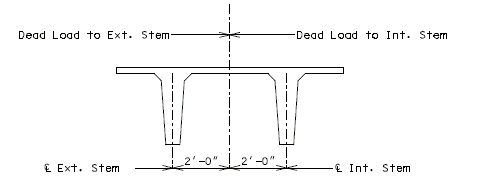
The non-composite dead load of the interior double tee girder
is divided evenly to each stem. A 9 lb./lin ft. dead load is
added to the non-composite dead load of each stem for
haunching. The non-composite dead load of C.I.P. slab, girder
and haunch are based on simple spans from Ë to Ë Bearings.
The composite dead load of the safety barrier is divided 75% to the exterior stem of the exterior girder and 25% to the interior stem of the exterior girder. No dead load due to the barrier curb is added to the interior girder. The composite dead load for future wearing surface is 35 lb./sq. ft. or 3" of material. The composite dead load of safety barrier curb, and future wearing surface are based on continuous, composite spans from Ë to Ë Bearings.
The live load design is based on HL93. The live load distribution factors are figured separate for exterior and interior Double Tee Girders. The assumption, that if the bridge is widened in the future the exterior girder then becomes an interior girder should be investigated.
Composite sections are adjusted for the difference in modulus of elasticity of slab and girder by multiplying by the factor (Eslab/Egirder). A 1" integral wearing surface is deducted for effective slab design.
Negative moment reinforcement is based on the amount required for the entire roadway width and not the amount required for each stem. The continuous span lengths are based on the distance from the Ë Bearing at End Bents to the Ë Interior Bent. The area of reinforcing bars is provided by adding bars between the normal longitudinal bars.
Continuity is obtained at intermediate supports by extending and bending all strands to form interlocking right angle hooks and pouring a concrete diaphragm monolithic with deck slab encasing the prestressed girders with the flange cut back at diaphragm.
Camber is based on simple spans. A transformed moment of inertia is figured for the total exterior or interior double tee girder since the total girder is cambered at the same rate.
Maximum horizontal curvature for Double-Tee structures is 3^. Outside flange edge of exterior girders on curved bridges is to be curved.
751.23.2 Details
751.23.2.1 Girder Dimensions
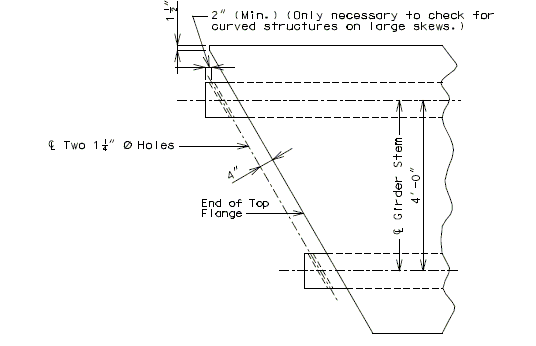
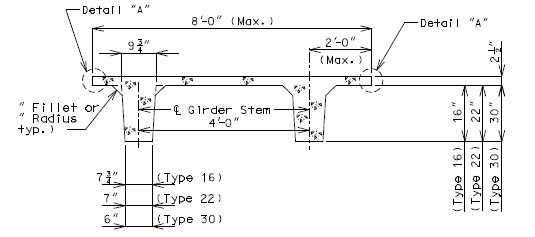
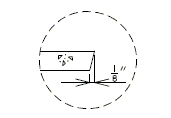
751.23.2.2 Vent Holes
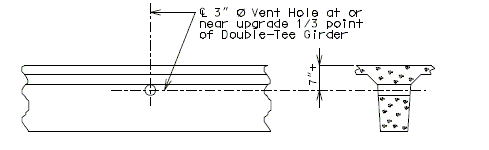
| Part Elevation of Girder Stem | ||||
751.23.2.3 Diaphragm Reinforcement
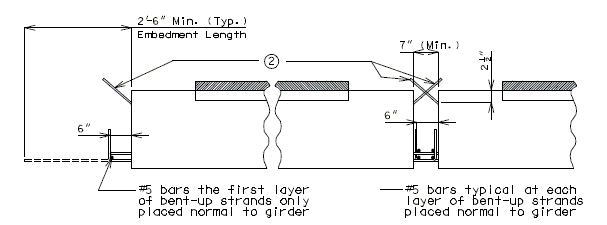
| End Bent | Int. Bent | |||
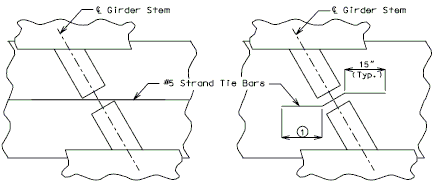
| Skew Thru 30 ø | Skew Over 30 ø | |||
751.23.2.4 Detail of Optional Construction Joint
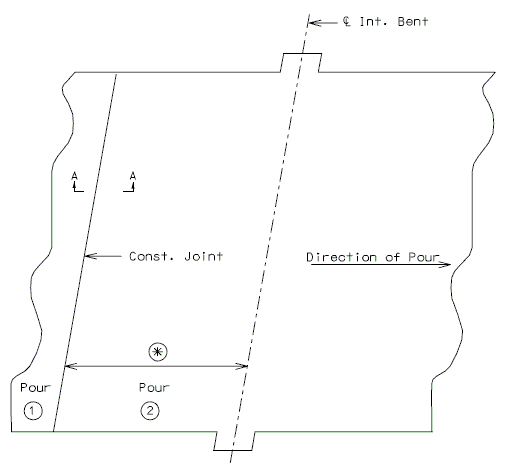
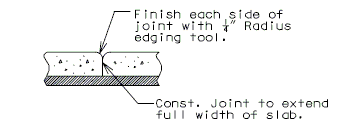
Place Const. Joint 6" from negative reinforcement in slab.
Note: Const. Joint placement will be determined by direction of slab pour.
751.23.2.5 Details for Curved Structures