751.37 Drilled Shafts
Contents
- 1 751.37.1 General
- 2 751.37.2 General Design Procedure and Limit States
- 3 751.37.3 Design for Axial Loading at Strength Limit State
- 3.1 751.37.3.1 Axial Resistance for Individual Drilled Shafts in Rock (qu ≥ 100 ksf)
- 3.2 751.37.3.2 Axial Resistance for Individual Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)
- 3.3 751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
- 3.4 751.37.3.4 Axial Resistance for Individual Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)
- 3.5 751.37.3.5 Axial Resistance for Individual Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
- 3.6 751.37.3.6 Axial Resistance for Individual Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
- 3.7 751.37.3.7 Axial Resistance for Individual Drilled Shafts in Cohesionless Soils
- 3.8 751.37.3.8 Geotechnical Resistance from Load Tests
- 3.9 751.37.3.9 Evaluation of Group Effects
- 4 751.37.4 Design for Axial Loading at Serviceability Limit States
- 5 751.37.5 Design for Lateral Loading at Strength and Service Limit States
- 6 751.37.6 Structural Resistance of Drilled Shafts
- 7 751.37.7 References
- 8 751.37.8 Commentary
- 8.1 Commentary on EPG 751.37.1 General
- 8.2 Commentary on EPG 751.37.2 General Design Procedure and Limit States
- 8.3 Commentary on EPG 751.37.3 Geotechnical Resistance for Axial Loading at Strength Limit States
- 8.3.1 Commentary on EPG 751.37.3.1 Axial Resistance for Individual Drilled Shafts in Rock (qu ≥ 100 ksf')
- 8.3.2 Commentary on EPG 751.37.3.2 Axial Resistance for Individual Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)
- 8.3.3 Commentary on EPG 751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
- 8.3.4 Commentary on EPG 751.37.3.4 Axial Resistance for Individual Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)
- 8.3.5 Commentary on EPG 751.37.3.5 Axial Resistance for Individual Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
- 8.3.6 Commentary on EPG 751.37.3.6 Axial Resistance for Individual Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
- 8.3.7 Commentary on EPG 751.37.3.7 Axial Resistance for Individual Drilled Shafts in Cohesionless Soils
- 8.3.8 Commentary on EPG 751.37.3.8 Geotechnical Resistance from Load Tests
- 8.3.9 Commentary on EPG 751.37.3.9 Evaluation of Group Effects
- 8.4 Commentary on EPG 751.37.4 Design for Axial Loading at Serviceability Limit States
- 8.4.1 Commentary on EPG 751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method
- 8.4.2 Commentary on EPG 751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method
- 8.4.3 Commentary on EPG 751.37.4.3 Settlement of Drilled Shafts in Groups
- 8.4.3.1 Commentary on Settlement of Shaft Groups in Cohesive Soils
- 8.4.3.2 Commentary on Settlement of Shaft Groups in Cohesionless Soils Using Standard Penetration Test Measurements
- 8.4.3.3 Commentary on Settlement of Shaft Groups in Cohesionless Soils Using Cone Penetration Test Measurements
- 8.4.3.4 Commentary on Settlement of Shaft Groups in Rock
- 8.5 Commentary on EPG 751.37.5 Design for Lateral Loading at Strength and Service Limit States
- 8.6 Commentary on EPG 751.37.6 Structural Resistance of Drilled Shafts
- 8.7 Commentary on EPG 751.37.7 References
751.37.1 General
| Commentary for EPG 751.37.1 General |
These guidelines address procedures for design of drilled shafts used as foundations for bridge piers, bridge abutments, roadway signs, and other miscellaneous structures. The guidelines were established following load and resistance factor design (LRFD) concepts. The provisions provided herein are intended to produce foundations that achieve target reliabilities established by MoDOT for structures of different operational importance. The four classes of operational importance include minor or low volume route, major route, major bridge costing less than $100 million, and major bridge costing greater than $100 million. Additional background regarding development of these provisions and supportive information regarding use of these provisions is provided in the accompanying commentary.
Drilled shafts can be an economical alternative to spread footing or driven pile foundations. They can be constructed in a wide variety of soil and rock conditions and designed to support a wide range of loading conditions. Drilled shafts should be considered:
- To accommodate sites where depth to bedrock is too short for pile embedment but too deep for spread footings.
- For large design loads. (Eliminates the need for large quantities of piles).
- To provide resistance against large lateral and uplift loads.
- To eliminate the need for cofferdams.
- To provide protection against scour.
- To accommodate concerns associated with the effects of pile driving (e.g. vibrations or interference with battered piles).
- When obstructions or other conditions may make pile driving difficult.
- To provide resistance to settlement when displacement tolerances are small.
751.37.1.1 Dimensions and Nomenclature
| Commentary for EPG 751.37.1.1 Dimensions and Nomenclature |
Dimensions to be established in design include the overall length of the shaft and the shaft diameter. For shafts that will be socketed into bedrock, the length and diameter of the rock socket must also be established. Table 751.37.1.1 defines the nomenclature used for these dimensions and provides relevant minimum and/or maximum values for the respective dimensions.
Table 751.37.1.1 Summary of drilled shaft dimensions with minimum and maximum values
| Dimension | Description | Minimum Value | Maximum Value | Comment |
|---|---|---|---|---|
| D | Nominal shaft diameter (Overall) | 18”1 | -- | Min. 6” increments |
| L | Length of shaft (Overall) | -- | -- | -- |
| Ds4 | Nominal socket diameter | -- | --2 | Min. 6” increments |
| Ls4 | Length of rock socket | Ds3, 5 | -- | -- |
| 1 Shaft diameter shall be at least 6” greater than column diameter when shaft is directly connected to the column and not a footing cap or bent cap. | ||||
| 2 Sockets installed through casing shall have diameters 6” less than the outside diameter of the casing. | ||||
| 3 Minimum rock socket length Ls ≥ Ds shall be measured from the anticipated tip of the casing. | ||||
| 4 The dimensions “Ds” and “Ls” are not explicitly used in any of the design equations that follow in favor of generally referring to the diameter of any segment of an overall shaft as “D” which can be a rock socket segment. This is not entirely true for the dimension “Ls” which is explicitly used as part of a settlement design equation that follows. Judicial use of the appropriate segment and use of the appropriate diameter and length of a segment is implicit to the correct use of the design equations that follow. (See EPG 751.37.2 General Design Procedure and Limit States.) | ||||
| 5 See Design Aid: Minimum Rock Socket Length | ||||
The length to diameter ratio of drilled shafts should generally be in the following range: 3 ≤ L/D ≤ 30
The nomenclature used in these guidelines has intentionally been selected to be consistent with that used in the AASHTO LRFD Bridge Design Specifications (AASHTO, 2009) to the extent possible to avoid potential confusion with methods provided in those specifications. By convention, references to other provisions of the MoDOT Engineering Policy Guide are indicated as “EPG XXX.XX” throughout these guidelines where the Xs are replaced with the appropriate article numbers. Similarly, references to provisions within the AASHTO LRFD Bridge Design Specifications are indicated as “LRFD XXX.XX”.
751.37.1.2 Materials
| Commentary for EPG 751.37.1.2 Materials |
Concrete used for drilled shaft construction shall be Class B-2 concrete with minimum compressive strength, = 4 ksi.
751.37.1.3 Casing
| Commentary for EPG 751.37.1.3 Casing |
All drilled shafts shall have permanent casing installed through overburden soils to prevent caving of these soils during construction unless conditions are such that the shafts can be more effectively and reliably constructed without casing or using temporary casing. Welded or seamless steel permanent casing shall be in accordance with Sec 701. Approval from the MoDOT Geotechnical Section is required for use of temporary casing or uncased shafts with or without drilling slurry.
Rock sockets shall be uncased.
Permanent Casing Thickness Design and Plan Reporting:
- Any drilled shaft for a major bridge over a river or lake or any drilled shaft longer than 80 feet or any drilled shaft greater than 6 feet in diameter shall have a minimum casing thickness of 1/2 inch specified unless a greater thickness is required by design for strength. The thickness of casing in either case shall be shown on the bridge plans and noted as a minimum.
- All other drilled shafts shall not have a minimum casing thickness specified unless a specific thickness is required by design for strength. The minimum thickness in the latter case shall be shown on the bridge plans and noted as a minimum.
- For drilled shaft stiffness computations and load distribution analysis, use the minimum casing thickness required. When a minimum casing thickness is not required, assume a casing thickness of 3/8” for the analysis.
751.37.1.4 General Design Considerations
| Commentary for EPG 751.37.1.4 General Design Considerations |
The following issues shall be considered for design of drilled shafts:
Scour
The potential for scour and its effect on the axial and lateral strength and serviceability of drilled shafts shall be investigated.
Ground Water
The effects of variable ground water levels and buoyancy shall be taken into account in evaluating drilled shaft strength and serviceability limit states.
Downdrag
Downdrag shall be considered when strength and serviceability are evaluated. For drilled shafts socketed into rock and overlain with soil that has the potential to settle, downdrag shall be considered as an applied load and predicted according to LRFD 3.11.8. Downward movements of 0.1 to 0.5 in. are enough to mobilize full downdrag. The top 5 ft. and a bottom length equal to the shaft diameter shall not be included in calculating downdrag. Allowance shall be given for an increase in the undrained shear strength of the soil within compressible strata as consolidation occurs.
Uplift
The effects of uplift shall be considered for drilled shafts in cohesive soils, not socketed into rock.
Group Effects
Shafts designed with relatively close spacing shall be evaluated considering group effects. Specific methods and modifications to account for group effects differ according to the soil/rock type that the shaft is founded within as provided in EPG 751.37.3.9.
The redundancy factor ηR from LRFD 1.3.4 shall not be applied for design of drilled shafts.
751.37.1.5 Related Provisions
| Commentary for EPG 751.37.1.5 Related Provisions |
The provisions of these guidelines were developed presuming that design parameters required to apply the provisions are established following current MoDOT site characterization protocols as described in EPG 321. Specific attention is drawn to EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. The provisions provided in these guidelines presume that parameter variability, as generally represented by the coefficient of variation (COV), is established following procedures in EPG 321.3.
751.37.1.6 Drilled Shaft General Detail Considerations
Pay items shown in above table are for example only, show actual pay items and quantities in plan details as per specific project.
Notes:
- (1) Number of pipes (equally spaced) for Sonic Logging Testing:
- Diameter ≤ 2.5 ft: 2 pipes
- Diameter >2.5 ft but ≤ 3.5 ft: 3 pipes
- Diameter >3.5 ft but ≤ 5.0 ft: 4 pipes
- Diameter >5.0 ft but ≤ 8.0 ft: 5 pipes
- Diameter >8.0 ft: 6 pipes
- Single diameter reinforcing cage is typically used. Modify details based on design for single or multiple-diameter cages and splice location(s).
- See EPG 751.37.1.3 for casing requirements and alternatives.
- When determining P bar diameter for barbill, assume 3/8” casing unless otherwise specified.
- See EPG 751.50, G8, for notes to include for drilled shafts and rock sockets (starting at G8.1).
- (2) See EPG 751.37.1.1 Dimensions and Nomenclature for Design Aid: Minimum Rock Socket Length.
- (1) Number of pipes (equally spaced) for Sonic Logging Testing:
| Bridge Standard Drawings |
| As Built Drilled Shaft Data |
751.37.2 General Design Procedure and Limit States
| Commentary for EPG 751.37.2 General Design Procedure and Limit States |
Drilled shafts should be sized (diameter and length) to support the required factored loads in the most cost effective manner possible without excessive deflections. The initial diameter and length of drilled shafts are generally established considering vertical loading at the strength limit state(s) according to EPG 751.37.3. The resulting shaft should then be evaluated at the axial and lateral serviceability limit states (settlement and lateral deflection) according to EPG 751.37.4 and EPG 751.37.5, where the shaft dimensions shall be adjusted if serviceability requirements are not satisfied.
The Strength Limit State and applicable Extreme Event Limit States shall be investigated when calculating the soil and structural resistance of the drilled shaft. The Service I Limit State shall be used when evaluating lateral deflection and settlement.
Guidance
There are three major types of drilled shaft construction that influence how a drilled shaft is designed. MoDOT exclusively designs and details drilled shafts with permanent casing and rock sockets as given as Case No. 1. The two cases that follow are rare and require the recommendation or approval of the Geotechnical Section and shall be shown on the plans. See EPG 751.37.1.3 Casing.
- 1. Permanently cased shaft through soil and socketed into rock. A reduced shaft diameter for rock socket is required. This case shall be used for all MoDOT projects unless otherwise allowed by the Geotechnical Section. For axial loading and settlement computations substitute D with Ds and L with Ls which are equal to the diameter and length of the rock socket since the required resistance to loading and settlement are computed for segment of the shaft in rock only (Rock sockets to be installed through casing shall have diameters 6” less than the inside diameter of the casing to allow for clearance and insertion of rock excavation re-tooling equipment.).
- 2. Permanently cased or temporarily cased or uncased shaft through soil and not socketed into rock. For axial loading and settlement computations use D = diameter of shaft.
- 3. Temporarily cased or uncased shaft through soil with a reduced or same shaft diameter for soil than/and for rock socket respectively. For axial loading and settlement computations use the appropriate diameter and length of shaft as the case may be for the design segment under investigation.
Permanently cased shafts shall not be allowed to use frictional resistance of the soil for either a drilled shaft with or without a rock socket.
Temporarily cased shafts may use the frictional resistance of the soil only for the case where a rock socket is not used (see the Geotechnical Section).
Recommendation or approval from the Geotechnical Section is required for use of temporary casing or uncased shafts with or without drilling slurry.
Note on Definitions:
- 1. Where L,i is defined, Li shall mean the length of the shaft segment through soil or through rock.
- 2. Where L is defined, L shall mean overall shaft length including the length of the rock socket.
751.37.3 Design for Axial Loading at Strength Limit State
| Commentary for EPG 751.37.3 Design for Axial Loading at Strength Limit State |
Geotechnical resistance to axial loading at the relevant strength limit state shall be computed as the sum of tip resistance and side resistance unless conditions are present that may prevent reliable mobilization of tip resistance (e.g. karst conditions with known or likely voids that cannot be specifically identified or characterized). Shafts should be sized such that the factored geotechnical resistance to axial loads exceeds the factored axial loads:
| (consistent units of force) | Equation 751.37.3.1 |
where:
- RR = factored axial shaft resistance (consistent units of force),
- RsR = factored side resistance (consistent units of force),
- RpR = factored tip resistance (consistent units of force) and
- = factored load for the appropriate strength limit state (consistent units of force).
Tip resistance and side resistance shall be computed according to the provisions of EPG 751.37.3 for the material type(s) encountered. The Structural Project Manager or Structural Liaison Engineer shall be consulted before utilizing design methods other than those provided in EPG 751.37.3 for calculating the geotechnical resistance of drilled shafts.
The factored side resistance for drilled shafts shall be established from factored unit side resistance values for the relevant soil/rock conditions as provided in this article. For stratified ground conditions or where the shaft dimensions change (e.g. at tip of temporary or permanent casing, or at top of rock socket), the shaft shall be divided into segments with practically uniform shaft geometry and soil/rock properties and unit side resistance values determined for each shaft segment. The total factored side resistance shall then be computed as the sum of the factored resistance values for each shaft segment:
| (consistent units of force) | Equation 751.37.3.2 |
where:
- n = number of shaft segments,
- = factored unit side resistance for shaft segment i (consistent units of stress),
- = perimeter interface area for shaft segment i (consistent units of area),
- = resistance factor for unit side resistance along shaft segment i (dimensionless),
- = nominal unit side resistance along shaft segment i (consistent units of stress),
- Di = shaft diameter for shaft segment i (consistent units of length), and
- Li = length of shaft segment i (consistent units of length).
and shall be determined in accordance with the provisions of this article, based on the material type present along the respective shaft segment.
Side resistance shall generally be neglected or reduced, as recommended by the Geotechnical Section, over shaft segments with permanent casing and over any length of rock socket that is deemed unusable.
The factored tip resistance for drilled shafts shall be established from factored unit tip resistance values for the relevant soil/rock conditions as provided in this article. The appropriate tip resistance shall be established for the soil/rock located between the tip of the shaft and two diameters below the tip of the shaft. The factored tip resistance shall be computed as
| (consistent units of force) | Equation 751.37.3.3 |
where:
- = factored unit tip resistance (consistent units of stress),
- = cross-sectional area of the shaft at the tip (consistent units of area),
- = resistance factor for unit tip resistance (dimensionless),
- = nominal unit tip resistance (consistent units of stress), and
- D = shaft diameter at the tip of the shaft (consistent units of length).
and shall be determined in accordance with the provisions of this article, based on the material type present within a depth of 2D below the tip of the shaft.
Tip resistance shall be neglected, as recommended by the Geotechnical Section, when the shaft tip is located within karstic rock or other conditions where tip resistance cannot be reliably determined.
The specific methods and resistance factors for determining nominal and factored side and tip resistance shall be selected based on the material type(s) present along the sides and beneath the tip of the shaft:
- EPG 751.37.3.1 shall generally be followed to estimate resistance for shafts in rock from results of uniaxial compression tests on intact rock core with uniaxial compressive strengths (qu ) greater than 100 ksf;
- EPG 751.37.3.2 shall generally be followed to estimate resistance for shafts in weak rock from results of uniaxial compression tests on rock core with uniaxial compressive strengths (qu ) greater than 5 ksf but less than 100 ksf;
- EPG 751.37.3.3 shall generally be followed to estimate resistance for shafts in weak rock from results of Standard Penetration Tests with equivalent N-values (Neq ) less than 400 blows/foot;
- EPG 751.37.3.4 shall generally be followed to estimate resistance for shafts in weak rock from results of Texas Cone Penetration Tests with measured penetrations (TCP) greater than 1 inch/100 blows but less than 10 inches/100 blows;
- EPG 751.37.3.5 shall generally be followed to estimate resistance for shafts in weak rock from results of Point Load Index Tests with Point Load Indices (Is(50) ) less than 40 ksf;
- EPG 751.37.3.6 shall generally be followed to estimate resistance for shafts in cohesive soils with undrained shear strengths (su ) less than 5 ksf; and
- EPG 751.37.3.7 shall generally be followed to estimate resistance for shafts in cohesionless soils.
Additional guidance on selection of specific methods and resistance factors based on the material types encountered is provided in the commentary to these guidelines.
751.37.3.1 Axial Resistance for Individual Drilled Shafts in Rock (qu ≥ 100 ksf)
| Commentary for EPG 751.37.3.1 Axial Resistance for Individual Drilled Shafts in Rock (qu ≥ 100 ksf) |
Side Resistance for Drilled Shafts in Rock (qu ≥ 100 ksf)
The nominal unit side resistance for shaft segments located in rock shall be computed as a function of the mean uniaxial compressive strength of the intact rock according to (Horvath and Kenney, 1979)
| (ksf) | Equation 751.37.3.4 |
where:
- qs = nominal unit side resistance for the shaft segment (ksf),
- = mean value of uniaxial compressive strength of rock core along the shaft segment (ksf), and
- = compressive strength of concrete (ksi).
- αE = factor to account for discontinuities in the rock
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qs ) determined according to the provisions of this article shall be established from Figure 751.37.3.1.1 based on the coefficient of variation of the mean uniaxial compressive strength . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over the length of the shaft segment. Values for should similarly reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Values for shall be estimated based on the expected concrete compressive strength for the shaft.
The nominal unit side resistance predicted using Equation 751.37.3.4 shall be limited to a maximum value of ksf where is input in units of ksi. This limit corresponds to 35 ksf for concrete with = 4 ksi.
A factor αE to account for discontinuities in the rock following O’Neill and Reese (1999) shall be used to reduce the nominal unit side resistance calculated by equation 751.37.3.4. The reduction factor shall only be applied to rock with recovery ratios less than 80% and RQD less than 50. Interpolation may be used. The reduction factor shall be determined and included as part of the nominal unit side resistance by the Geotechnical Section.
| RQD | αE | |
|---|---|---|
| Closed Joints | Open Joints | |
| 100 | 1.0 | 0.85 |
| 70 | 0.85 | 0.55 |
| 50 | 0.60 | 0.55 |
| 30 | 0.50 | 0.5 |
| 20 | 0.45 | 0.45 |
Tip Resistance for Drilled Shafts in Rock (qu ≥ 100 ksf)
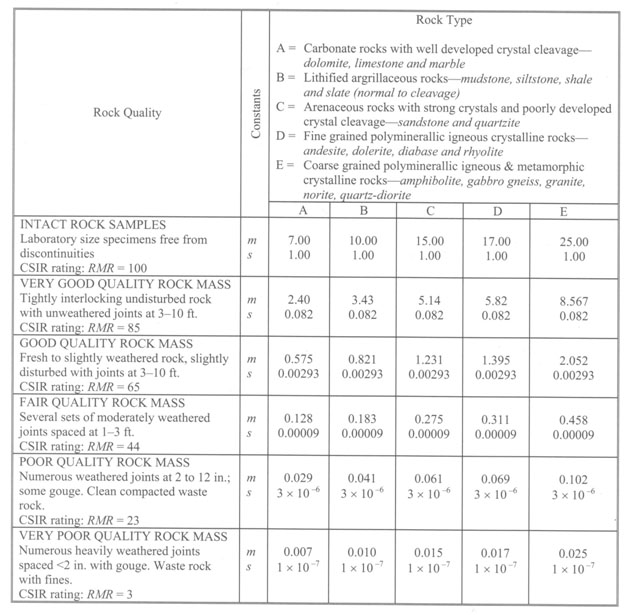
The nominal unit tip resistance for shafts founded on rock shall be computed as (adapted from Wyllie, 1999)
| (consistent units of stress) | Equation 751.37.3.5 |
where:
- qp = nominal unit tip resistance for the shaft (consistent units of stress),
- = mean value of the uniaxial compressive strength (consistent units of stress) and
- m and s = empirical constants describing the rock mass strength (dimensionless).
Resistance factors to be applied to the nominal resistance values (qp) determined according to the provisions of this article shall be established from Figure 751.37.3.1.2 based on the coefficient of variation of the mean uniaxial compressive strength . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for , m and s shall be taken as mean values for the rock over a depth of 2Ds below the tip of the shaft. Values for should similarly reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Values for the rock mass parameters m and s can be established as:
| (dimensionless) | Equation 751.37.3.6 | |
| (dimensionless) | Equation 751.37.3.7a | |
| (dimensionless) | Equation 751.37.3.7b |
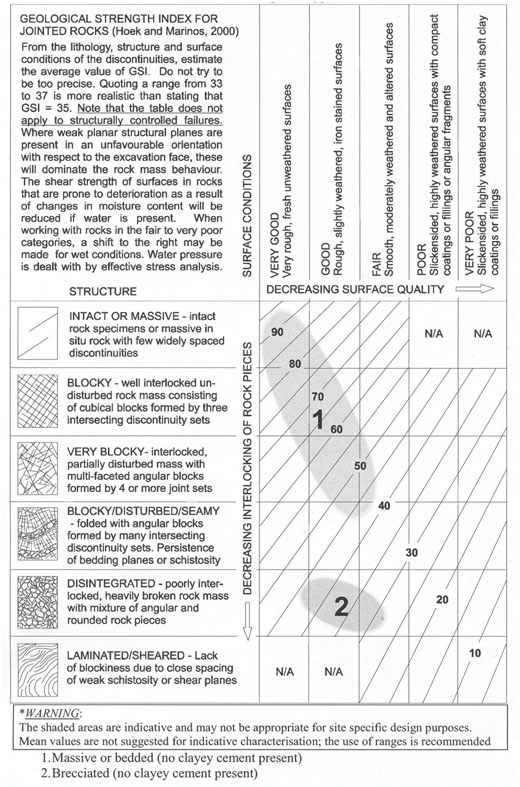
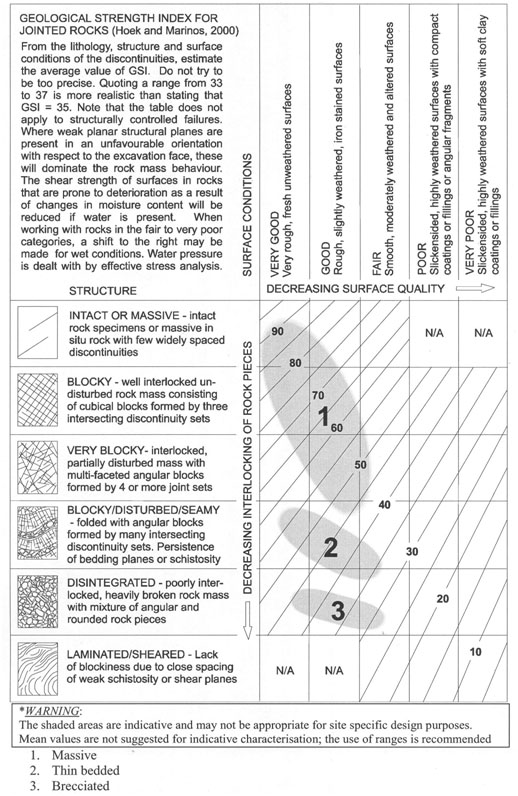
where mi is a material constant corresponding to rock type and GSI is the Geological Strength Index. The value for mi can be estimated from Table 751.37.3.1.2 or determined more precisely from triaxial tests (Hoek and Brown, 1997). For routine design, mi can be approximated as 10 for limestones and dolomites, as 6 for shales, siltstones, and mudstones, and as 17 for sandstones. Values for GSI can be estimated from rock mass characterizations using the Rock Mass Rating (RMR) system for rock masses with RMR greater than 25 (Hoek and Brown, 1997). Using this approach, GSI is calculated as:
| (dimensionless) | Equation 751.37.3.8 |
where
Ri = Rock Mass Rating system rating parameters (dimensionless).
GSI is thus equivalent to the RMR value with the groundwater rating term, R5, taken as 10.
Values for GSI to be used in Equations 751.37.3.6 and 751.37.3.7, or values for m and s to be used in Equation 751.37.3.5, can also be established using alternative methods described in the commentary to this subarticle.
The nominal tip resistance predicted using Equation 751.37.3.5 shall be limited to a maximum value of 400 ksf unless greater resistance can be verified by a load test.
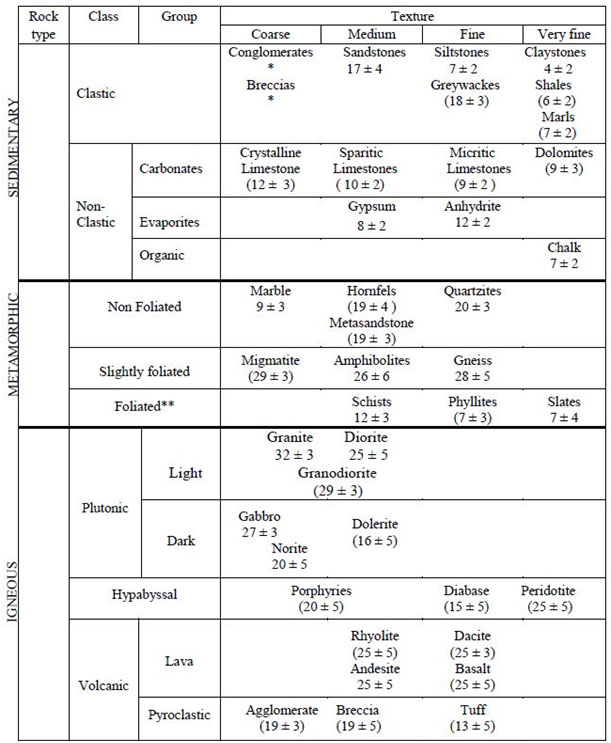
* Conglomerates and breccias may present a wide range of mi values depending on the nature of the cementing material and degree of cementation, so they may range from values similar to sandstone, to values used for fine grained sediments (even under 10).
** These values are for intact rock specimens tested normal to bedding or foliation. The value of mi will be significantly different if failure occurs along a weakness plane.
751.37.3.2 Axial Resistance for Individual Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)
| Commentary on EPG 751.37.3.2 Axial Resistance for Individual Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf) |
Side Resistance for Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)
The nominal unit side resistance for shaft segments located in weak rock shall be computed from measurements of uniaxial compressive strength on rock core as (Loehr et al., 2011a; Loehr et al., 2011b)
| (ksf) | Equation 751.37.3.9 |
where:
- qs = nominal unit side resistance for the shaft segment (ksf) and
- = mean uniaxial compressive strength of rock core along the shaft segment (ksf).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qs) determined according to the provisions of this article shall be established from Figure 751.37.3.2.1 based on the coefficient of variation of the mean uniaxial compressive strength . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over the length of the shaft segment. Values for should similarly reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment.
The nominal unit side resistance predicted using Equation 751.37.3.9 shall be limited to a maximum value of 30 ksf unless greater resistance can be verified by a load test.
Tip Resistance for Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)
The nominal unit tip resistance for shafts founded on weak rock shall be computed from measurements of uniaxial compressive strength on rock core as (Loehr et al., 2011a; Loehr et al., 2011b)
| (ksf) | Equation 751.37.3.10 |
where:
- qp = nominal unit tip resistance for the shaft (ksf), and
- = mean uniaxial compressive strength for rock at the shaft tip (ksf).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qp) determined according to the provisions of this article shall be established from Figure 751.37.3.2.2 based on the coefficient of variation of the mean uniaxial compressive strength . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over a depth of 2Ds below the tip of the shaft. Values for should similarly reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
The nominal tip resistance predicted using Equation 751.37.3.10 shall be limited to a maximum value of 400 ksf unless greater resistance can be verified by a load test.
751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
| Commentary for EPG 751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft) |
Side Resistance for Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
The nominal unit side resistance for shaft segments located in weak rock shall be computed from Standard Penetration Test (SPT) measurements as (Pierce et al., 2011)
| (ksf) | Equation 751.37.3.11 |
where:
- qs = nominal unit side resistance for the shaft segment (ksf) and
- = equivalent SPT N-value along the shaft segment (blows/foot).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qs) determined according to the provisions of this article shall be established from Figure 751.37.3.3.1 based on the coefficient of variation of the mean equivalent SPR N-value . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over the length of the shaft segment. Values for should similarly reflect the variability of the mean equivalent N-value for the rock over the shaft segment.
The nominal unit side resistance predicted using Equation 751.37.3.11 shall be limited to a maximum value of 30 ksf unless greater resistance can be verified by a load test.
Tip Resistance for Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
The nominal unit tip resistance for shafts founded on weak rock shall be computed from Standard Penetration Test (SPT) measurements as (Pierce et al., 2011)
| (ksf) | Equation 751.37.3.9 |
where:
- qp = nominal unit tip resistance for the shaft (ksf) and
- = mean equivalent SPT N-value for rock at the shaft tip (blows/foot).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qp) determined according to the provisions of this article shall be established from Figure 751.37.3.3.2 based on the coefficient of variation of the mean equivalent SPR N-value . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over a depth of 2Ds below the tip of the shaft. Values for should similarly reflect the variability of the mean equivalent N-value for the rock over the distance 2Ds below the tip of the shaft.
The nominal tip resistance predicted using Equation 751.37.3.12 shall be limited to a maximum value of 400 ksf unless greater resistance can be verified by a load test.
751.37.3.4 Axial Resistance for Individual Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)
| Commentary for EPG 751.37.3.4 Axial Resistance for Individual Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.) |
Side Resistance for Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)
The nominal unit side resistance for shaft segments located in weak rock shall be computed from Texas Cone Penetration Test (TCPT) measurements as (Pierce et al., 2011)
| (ksf) | Equation 751.37.3.13 |
where:
- qs = nominal unit side resistance for the shaft segment (ksf) and
- = mean value of penetration from TCPT measurements for rock along the shaft segment (inches/100 blows).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qs) determined according to the provisions of this article shall be established from Figure 751.37.3.4.1 based on the coefficient of variation of the mean TCP-value . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over the length of the shaft segment. Values for should similarly reflect the variability of the mean TCP-value for the rock over the shaft segment.
The nominal unit side resistance predicted using Equation 751.37.3.13 shall be limited to a maximum value of 30 ksf unless greater resistance can be verified by a load test.
Tip Resistance for Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)
The nominal unit tip resistance for shafts founded on weak rock shall be computed from Texas Cone Penetration Test (TCPT) measurements as (Pierce et al., 2011)
| (ksf) | Equation 751.37.3.14 |
where:
- (qp) = nominal unit tip resistance for the shaft (ksf) and
- = mean value of penetration from TCPT measurements for rock at the tip of the shaft (inches/100 blows).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qp) determined according to the provisions of this article shall be established from Figure 751.37.3.4.2 based on the coefficient of variation of the mean TCP-value . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over a depth of 2Ds below the tip of the shaft. Values for should similarly reflect the variability of the mean TCP-value for the rock over the distance 2Ds below the tip of the shaft.
The nominal tip resistance predicted using Equation 751.37.3.14 shall be limited to a maximum value of 400 ksf unless greater resistance can be verified by a load test.
751.37.3.5 Axial Resistance for Individual Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
| Commentary for EPG 751.37.3.5 Axial Resistance for Individual Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf) |
Side Resistance for Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
The nominal unit side resistance for shaft segments located in weak rock shall be computed from Point Load Index Test measurements as (Loehr et al., 2011a; Loehr et al., 2011b)
| (ksf) | Equation 751.37.3.15 |
where:
- qs = nominal unit side resistance for the shaft segment (ksf) and
- = mean corrected point load index value for rock along the shaft segment (ksf).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qs) determined according to the provisions of this article shall be established from Figure 751.37.3.5.1 based on the coefficient of variation of the mean Is(50)-value . Values for Is(50) and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for Is(50) shall be taken as mean values for the rock over the length of the shaft segment. Values for should similarly reflect the variability of the mean Is(50)-value for the rock over the shaft segment.
The nominal unit side resistance predicted using Equation 751.37.3.15 shall be limited to a maximum value of 30 ksf unless greater resistance can be verified by a load test.
Tip Resistance for Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
The nominal unit tip resistance for shafts founded on weak rock shall be computed from Point Load Index Test measurements as (Loehr et al., 2011a; Loehr et al., 2011b)
| (ksf) | Equation 751.37.3.16 |
where:
- qp = nominal unit tip resistance for the shaft (ksf) and
- = mean corrected point load index value for rock at the tip of the shaft (ksf).
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qp) determined according to the provisions of this article shall be established from Figure 751.37.3.5.2 based on the coefficient of variation of the mean Is(50)-value . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the rock over a depth of 2Ds below the tip of the shaft. Values for should similarly reflect the variability of the mean Is(50)-value for the rock over the distance 2Ds below the tip of the shaft.
The nominal tip resistance predicted using Equation 751.37.3.16 shall be limited to a maximum value of 400 ksf unless greater resistance can be verified by a load test.
751.37.3.6 Axial Resistance for Individual Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
| Commentary for EPG 751.37.3.6 Axial Resistance for Individual Drilled Shafts in Cohesive Soils (su ≤ 5 ksf) |
Side Resistance for Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
The nominal unit side resistance for shaft segments located in cohesive soils shall be computed from measurements of undrained shear strength using the “α-method” as (e.g. Reese et al., 2006)
| (consistent units of stress) | Equation 751.37.3.17 |
where:
- qs = nominal unit side resistance for the shaft segment (consistent units of stress),
- α = an empirical coefficient (dimensionless) and
- = mean value of the undrained shear strength for the soil along the shaft segment (consistent units of stress).
The value for α shall be taken as
| (dimensionless) | Equation 751.37.3.18 |
where is the mean undrained shear strength input in units of ksf.
Note that this expression is dimensional so values must be entered in the units specified.
Resistance factors to be applied to the nominal resistance values (qs) determined according to the provisions of this article shall be established from Figure 751.37.3.6.1 based on the coefficient of variation of mean undrained shear strength . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the soil over the length of the shaft segment. Values for should similarly reflect the variability of the mean undrained shear strength for the soil over the shaft segment.
The value for α predicted using Equation 751.37.3.18 shall be limited to a maximum value of 1.0.
In cohesive soils, side resistance along the top 5 ft. of the shaft and a distance of one shaft diameter above the tip of the shaft shall be ignored.
Tip Resistance for Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
The nominal tip resistance for shafts founded on cohesive soils shall be calculated from measurements of undrained shear strength according to:
| (consistent units of stress) | Equation 751.37.3.19 |
where:
- qp = nominal unit tip resistance for the shaft (consistent units of stress),
- = mean value of the undrained shear strength of the soil (consistent units of stress) and
- Nc = bearing capacity factor (dimensionless).
Resistance factors to be applied to the nominal resistance values (qp) determined according to the provisions of this article shall be established from Figure 751.37.3.6.2 based on the coefficient of variation of the mean undrained shear strength . Values for and shall be determined in accordance with methods described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation for the site and location in question. Values for shall be taken as mean values for the soil over a depth of 2D below the tip of the shaft. Values for should similarly reflect the variability of the mean undrained shear strength for the soil over the distance 2D below the tip of the shaft.
The value for Nc shall be taken as
| (dimensionless) | Equation 751.37.3.20 |
where:
- Z = depth of the tip of the shaft from the ground surface (consistent units of length), and
- D = shaft diameter (consistent units of length).
The value for Nc predicted using Equation 751.37.3.20 shall be limited to a maximum value of 9.0.
For ≤ 0.5 ksf, Nc shall be multiplied by 0.67.
The nominal unit tip resistance predicted using Equation 751.37.3.19 shall be limited to a maximum value of 80 ksf unless greater resistance can be verified by a load test.
751.37.3.7 Axial Resistance for Individual Drilled Shafts in Cohesionless Soils
| Commentary for EPG 751.37.3.7 Axial Resistance for Individual Drilled Shafts in Cohesionless Soils |
Side Resistance for Drilled Shafts in Cohesionless Soils
The nominal unit side resistance for shaft segments located in cohesionless soils shall be computed using the “β-method” as
| (consistent units of stress) | Equation 751.37.3.21 |
where:
- qs = nominal unit side resistance for the shaft segment (consistent units of stress),
- β = an empirical correlation factor (dimensionless) and
- σ'v = average vertical effective stress for the soil along the shaft segment (consistent units of stress).
The value for β shall be taken as (O’Neill and Reese, 1999)
| (for N60 ≥ 15) | Equation 751.37.3.22a | |
| (for N60 < 15) | Equation 751.37.3.22b |
where 0.25 ≤ β ≤ 1.2 and
- z = depth below ground surface to center of shaft segment (ft.) and
- N60 = average SPT N-value corrected for hammer efficiency (blows/ft).
If permanent casing is used, the side resistance shall be adjusted with consideration of type and length of casing used.
The resistance factor to be applied to the nominal unit side resistance shall be taken as 0.55.
Tip Resistance for Drilled Shafts in Cohesionless Soils
The nominal unit tip resistance for shafts founded on cohesionless soils shall be computed from corrected SPT N-values, N60 (O’Neill and Reese, 1999).
For N_60≤50:
| (ksf) | Equation 751.37.3.23 |
where:
- qp = nominal unit tip resistance for the shaft (ksf) and
- N60 = average SPT N-value corrected for hammer efficiency (blows/ft).
For N60 ≥ 50:
| (ksf) | Equation 751.37.3.24 |
where:
- qp = nominal unit tip resistance for the shaft (ksf),
- N60 = average SPT N-value corrected for hammer efficiency (blows/foot),
- pa = 2.12 ksf = atmospheric pressure (ksf).
- = vertical effective stress for the soil at the tip of the shaft (ksf).
Note that these expressions are dimensional so values must be entered in the units specified.
The resistance factor shall be taken as 0.50 for Equation 751.37.3.23 and as 0.55 for Equation 751.37.3.24.
751.37.3.8 Geotechnical Resistance from Load Tests
| Commentary for EPG 751.37.3.8 Geotechnical Resistance from Load Tests |
If drilled shaft resistance is determined by load test, the resistance factor shall be taken as 0.7 regardless of the soil conditions.
751.37.3.9 Evaluation of Group Effects
| Commentary for EPG 751.37.3.9 Evaluation of Group Effects |
Group effects for drilled shafts shall be evaluated as described in EPG 751.37.3.9. Procedures for evaluation of group effects generally involve use of a group efficiency factor, consideration of an “equivalent pier”, or both. Application of the group efficiency factor requires that the nominal resistance for individual shafts be multiplied by the factor η to reflect the nominal average resistance of the shafts within a group:
| (consistent units of force) | Equation 751.37.3.25 |
where:
- R = nominal resistance of an individual shaft (consistent units of force),
- R* = modified shaft resistance accounting for group effects (consistent units of force) and
- η = group efficiency factor established as described in this article.
Note that the group efficiency factor (η) used here is different from the redundancy factor (ηR) discussed in EPG 751.37.1.4. Additional discussion regarding the redundancy factor is provided in the commentary.
Consideration of an “equivalent pier” requires evaluation of the shaft group as a hypothetical, monolithic pier encompassing the block of soil and shafts enclosed within the outer perimeter of the shaft group.
The specific method to be used differs with geologic setting as described in the remainder of this article.
Group Effects in Cohesionless Soils
For shafts deriving resistance predominantly from cohesionless soils, the nominal resistance of individual shafts in the group shall be reduced by an efficiency factor, η, determined based on the spacing of the shafts:
- for shafts with center-to-center spacing equal to 2.5 shaft diameters, η = 0.65
- for shafts with center-to-center spacing equal to 4.0 shaft diameters or more, η = 1.0, and
- for shafts with intermediate spacing, the value for η shall be linearly interpolated between these values.
These efficiency factors shall apply regardless of conditions of contact between the cap and ground.
Group Effects in Cohesive Soils
For shafts deriving resistance predominantly from cohesive soils, the nominal resistance of the pile group shall be taken as the lesser of the following values:
- The nominal resistance of an equivalent pier consisting of the shafts and the block of soil within the area bounded by the shafts, or
- The sum of the nominal resistances for each individual shaft in the group.
For the latter value, the nominal resistances for individual piles shall be reduced by an efficiency factor, η, if the soil is soft and the cap may not be in firm contact with the ground. In such cases, the efficiency factor, η, shall be determined based on the spacing of the shafts:
- η = 0.65 for shafts with center-to-center spacing equal to 2.5 shaft diameters,
- η = 1.0 for shafts with center-to-center spacing equal to 6.0 shaft diameters or more, and
- For intermediate shaft spacing, the value for η shall be linearly interpolated between these values.
Note that the efficiency factors shall only apply if the soil is soft and the cap is not in firm contact with the ground. For all other conditions, no efficiency factor shall be applied when comparing the total resistance for the equivalent pier with the cumulative resistance from the individual shafts.
The resistance factors to be applied for the equivalent pier evaluation shall be 0.60 (AASHTO, 2009). Resistance factors for summation of the individual shaft resistances shall be those provided in EPG 751.37.3.1 through EPG 751.37.3.8.
Group Effects in Rock
For shafts deriving resistance predominantly from rock, the nominal resistance of the pile group shall be taken as the lesser of the following:
- The nominal resistance of an equivalent pier consisting of the shafts and the block of soil/rock within the area bounded by the shafts, or
- The sum of the nominal resistances for each individual shaft in the group.
No efficiency factor shall be applied to the individual pile resistances when evaluating the latter condition.
751.37.4 Design for Axial Loading at Serviceability Limit States
| Commentary for EPG 751.37.Commentary on EPG 751.37.4 Design for Axial Loading at Serviceability Limit States |
Drilled shafts shall be dimensioned so that there is a small likelihood that shafts will settle more than tolerable settlements, generally established from consideration of span length. This shall be accomplished by comparing a factored settlement computed for a shaft with dimensions established from EPG 751.37.3 with an established tolerable settlement. If the factored total settlement determined from these provisions is found to be less than or equal to the tolerable settlement, i.e. if
| (consistent units of lengths) | Equation 751.37.4.1 |
where:
- δR = factored total settlement (consistent units of length) and
- δtol = tolerable settlement (consistent units of length),
the limit state is satisfied and the probability of shaft settlement exceeding the tolerable settlement is less than or equal to the target probability established by MoDOT. If the factored total settlement is determined to exceed the tolerable settlement, the probability of foundation settlement exceeding the tolerable value is greater than the target probability established by MoDOT. In such cases, the shaft dimensions shall be increased until the factored total settlement is less than or equal to the tolerable settlement.
Resistance factors provided in this article were established to produce factored settlements that have a target probability of being exceeded. Target probabilities of exceedance were established by MoDOT for structures of different operational importance. Additional information regarding development of the resistance factors and application of the resistance factors for settlement calculations are provided in the commentary that accompanies these guidelines.
For this provision, the tolerable settlement shall be taken as
| (consistent units of lengths) | Equation 751.37.4.2 |
where:
- δtol = tolerable settlement (consistent units of length) and
- S = span between adjacent bridge bents (consistent units of length).
Factored settlements shall be determined as provided in this article. Settlement shall be evaluated for the Service I limit state.
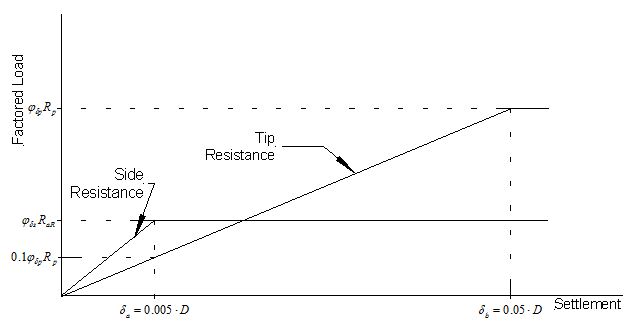
Two alternative approaches are provided in these guidelines for determining the factored total settlement of drilled shafts. The first approach is based on an approximate factored load-settlement relationship for an individual shaft. The second approach utilizes the “t-z” method to predict the factored settlement for the shaft. Greater factored settlements will generally be predicted using the approximate method both because it tends to be conservative at working loads and because it involves greater variability and uncertainty. It is expected that the approximate method will generally be used for preliminary evaluation of settlement. If the settlement determined from the approximate method satisfies the serviceability requirement of Equation 751.37.4.1, the shaft dimensions can be considered acceptable. If use of the approximate method produces factored settlements that do not satisfy Equation 751.37.4.1, designers should consider performing evaluations using the more precise t-z method to evaluate whether serviceability is satisfied prior to increasing the dimensions of the shaft to satisfy serviceability requirements.
751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method
| Commentary on EPG 751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method |
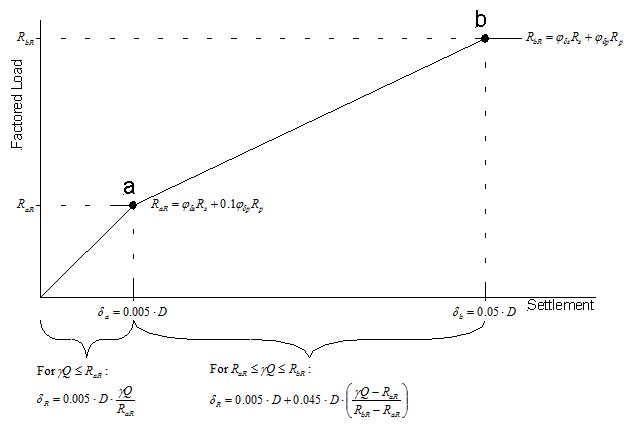
Prediction of factored settlement due to factored service loads shall be determined as follows depending on the magnitude of factored loads relative to the magnitude of factored side and tip resistance:
If :
| (consistent units of lengths) | Equation 751.37.4.3 |
where:
- = factored load for the appropriate serviceability limit state (consistent units of force),
- RsR = total factored side resistance determined according to the provisions of this article (consistent units of force),
- RpR = factored tip resistance determined according to the provisions of this article (consistent units of force),
- δR = factored total settlement of shaft due to factored service loads (consistent units of length),
- D = shaft diameter (consistent units of length) and
- δeR = factored elastic compression of the unsupported length of the shaft (consistent units of length).
If :
| (consistent units of lengths) | Equation 751.37.4.4 |
where:
- = factored load for the appropriate serviceability limit state (consistent units of force),
- RsR = total factored side resistance determined according to the provisions of this article (consistent units of force),
- RpR = factored tip resistance determined according to the provisions of this article (consistent units of force),
- δR = factored total settlement of shaft due to factored service load (consistent units of length),
- D = shaft diameter (consistent units of length) and
- δeR = factored elastic compression of the unsupported length of the shaft (consistent units of length).
Note that if , the factored service load exceeds the maximum factored resistance of the shaft and the limit state cannot be satisfied without increasing the dimensions of the shaft.
The factored side resistance in Equations 751.37.4.3 and 751.37.4.4 shall be established from factored unit side resistance values for the relevant soil/rock conditions as provided in this article. For stratified ground conditions or where the shaft dimensions change (e.g. at tip of temporary or permanent casing, or at top of rock socket), the shaft shall be divided into segments with practically uniform shaft geometry and soil/rock properties and unit side resistance values determined for each shaft segment. The total factored side resistance shall then be computed as the sum of the factored resistance values for each shaft segment:
| (consistent units of force) | Equation 751.37.4.5 |
where:
- n = number of shaft segments,
- = factored unit side resistance for shaft segment i (consistent units of stress),
- = perimeter interface area for shaft segment i (consistent units of area),
- = settlement resistance factor for side resistance along shaft segment i (dimensionless),
- qs-i = nominal unit side resistance along shaft segment i (consistent units of stress),
- Di = shaft diameter for shaft segment i (consistent units of length) and
- Li = length of shaft segment i (consistent units of length).
Values for qs-i shall be determined in accordance with the provisions of EPG 751.37.3, based on the material type present along the respective shaft segments. Values for shall be established as provided subsequently in this article. Side resistance shall generally be neglected or reduced, as recommended by the Geotechnical Section, over shaft segments with permanent casing and over any length of rock socket that is deemed unusable for consistency with evaluations performed for strength limit states.
The factored tip resistance in Equations 751.37.4.3 and 751.37.4.4 shall be established from factored unit tip resistance values for the relevant soil/rock conditions as provided in this article. The appropriate tip resistance shall be established for the soil/rock located between the tip of the shaft and a distance of 2D below the tip of the shaft. The factored tip resistance shall be computed as
| (consistent units of force) | Equation 751.37.4.6 |
where:
- = factored unit tip resistance (consistent units of stress),
- = cross-sectional area of the shaft at the tip (consistent units of area),
- = settlement resistance factor for tip resistance (dimensionless),
- qp = nominal unit tip resistance (consistent units of stress) and
- D = shaft diameter at the tip of the shaft (consistent units of length).
The value for qp shall be determined in accordance with the provisions of EPG 751.37.3, based on the material type present within a depth of 2D below the tip of the shaft. The value for shall be established as provided subsequently in this article. For consistency with evaluations for strength limit states, tip resistance shall be neglected, as recommended by the Geotechnical Section, when the shaft tip is located within karstic rock or other conditions where tip resistance cannot be reliably determined.
The factored elastic compression of the unsupported length of the shaft shall be determined as
| (consistent units of length) | Equation 751.37.4.7 |
where:
- δeR = factored elastic compression of the unsupported length of the shaft (consistent units of length),
- = factored load for the appropriate serviceability limit state (consistent units of force),
- L = overall shaft length (consistent units of length),
- Ls = length of the rock socket (consistent units of length),
- Ep = nominal modulus of elasticity for the shaft (consistent units of stress),
- Ap = nominal shaft area (consistent units of area) and
- = settlement resistance factor for elastic compression of the shaft.
Values for the settlement resistance factor for elastic compression of the shaft shall be taken from Table 751.37.4.1 according to the operational importance of the structure.
Table 751.37.4.1 Settlement resistance factors for elastic compression of drilled shafts
| Operational Importance | Settlement Resistance Factor, Φδe |
|---|---|
| Minor or Low Volume Route | 0.68 |
| Major Route | 0.64 |
| Major Bridge <$100 million | 0.61 |
| Major Bridge >$100 million | 0.60 |
Settlement Resistance Factors for Approximate Method for Drilled Shafts in Rock
Settlement resistance factors to be applied to side resistance for shaft segments through rock shall be determined from Figure 751.37.4.1.1 based on the coefficient of variation of the mean uniaxial compressive strength, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on rock shall similarly be determined from Figure 751.37.4.1.2 based on values for that reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for Approximate Method for Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.1.3 based on the coefficient of variation of the mean uniaxial compressive strength, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.1.4 based on values for that reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for Approximate Method for Drilled Shafts in Weak Rock from Standard Penetration Test Measurements
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.1.5 based on the coefficient of variation of the mean equivalent SPT N-value, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean equivalent N-value over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.1.6 based on values for that reflect the variability of the mean equivalent N-value over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for Approximate Method for Drilled Shafts in Weak Rock from Texas Cone Penetration Test Measurements
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.1.7 based on the coefficient of variation of the mean TCP-value, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean TCP-value over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.1.8 based on values for that reflect the variability of the mean TCP-value over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for Approximate Method for Drilled Shafts in Weak Rock from Point Load Index Test Measurements
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.1.9 based on the coefficient of variation of the mean Is(50)-value, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean Is(50)-value for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.1.10 based on values for that reflect the variability of the mean Is(50)-value for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for Approximate Method for Drilled Shafts in Cohesive Soils
Settlement resistance factors to be applied to side resistance for shaft segments through cohesive soil shall be determined from Figure 751.37.4.1.11 based on the coefficient of variation of the mean undrained shear strength, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean undrained shear strength for the soil over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on cohesive soil shall similarly be determined from Figure 751.37.4.1.12 based on values for that reflect the variability of the mean undrained shear strength for the soil over the distance 2D below the tip of the shaft.
For shafts founded in soft cohesive soils, consideration shall also be given to including additional settlement induced from time dependent consolidation of the soil.
Settlement Resistance Factors for Approximate Method for Drilled Shafts in Cohesionless Soils
Settlement evaluations for individual drilled shafts in cohesionless soils shall be designed according to applicable sections of the current AASHTO LRFD Bridge Design Specifications.
751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method
| Commentary on EPG 751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method |
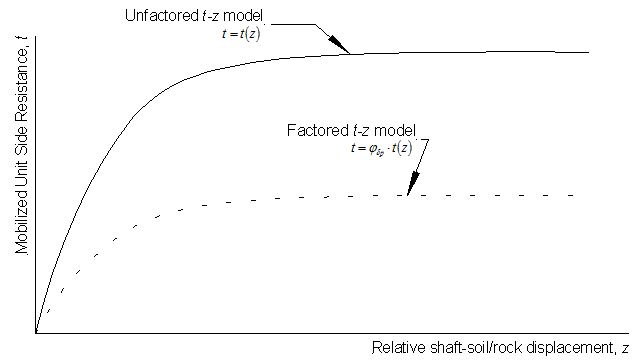
The “t-z method” is a numerical method for predicting the axial load-displacement response of drilled shafts and other deep foundation members (Reese et al., 2006). The analyses can be performed using commercial specialty software, such as TZPile©, or using common spreadsheet software. Regardless of the method of implementation, the analyses require specification of t-z models that reflect the load transfer characteristics for side resistance, “q-w” models that reflect the load transfer characteristics for tip resistance, and shaft characteristics that reflect the stiffness of the shaft relative to the surrounding soil/rock.
Prediction of factored settlements using the t-z method according to these provisions shall be accomplished by performing t-z analysis using factored t-z and q-w models models as described in more detail in the commentary to this article. The top of shaft settlement predicted using the t-z method for a shaft subjected to the factored service loads and modeled using factored t-z and q-w models shall be taken as the factored total settlement, δR, for use in Equation 751.37.4.1.
Factored t-z models shall be established from a nominal, unfactored t-z model selected to represent the load transfer response in side resistance for relevant soil/rock conditions as
| (consistent units of stress) | Equation 751.37.4.8 |
where:
- tR(z) = factored t-z model for input into analyses using the t-z method (consistent units of stress),
- z = relative displacement between the shaft and the soil/rock along the length of the shaft (consistent units of length),
- = settlement resistance factor for side resistance (dimensionless) and
- t(z) = nominal t-z model selected to represent relevant soil/rock conditions (consistent units of stress).
Values for shall be established according to the soil/rock type and available site characterization data as provided subsequently in this article.
Factored q-w models shall similarly be established from a nominal, unfactored q-w model selected to represent the load transfer response in tip resistance for relevant soil/rock conditions as
| (consistent units of stress) | Equation 751.37.4.9 |
where:
- qR(w) = factored q-w model for input into analyses using the t-z method (consistent units of stress),
- w = relative displacement between the shaft and the soil/rock at the shaft tip (consistent units of length),
- = settlement resistance factor for tip resistance (dimensionless), and
- q(w) = nominal q-w model selected to represent relevant soil/rock conditions at the tip of the shaft (consistent units of stress).
Values for shall be established according to the soil/rock type and available site characterization data as provided subsequently in this article.
Settlement Resistance Factors for t-z Method for Drilled Shafts in Rock
Settlement resistance factors to be applied to side resistance for shaft segments through rock shall be determined from Figure 751.37.4.2.1 based on the coefficient of variation of the mean uniaxial compressive strength, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on rock shall similarly be determined from Figure 751.37.4.2.2 based on values for that reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for t-z Method for Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.2.3 based on the coefficient of variation of the mean uniaxial compressive strength, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.2.4 based on values for that reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for t-z Method for Drilled Shafts in Weak Rock from Standard Penetration Test Measurements
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.2.5 based on the coefficient of variation of the mean equivalent SPT N-value, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.2.6 based on values for that reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for t-z Method for Drilled Shafts in Weak Rock from Texas Cone Penetration Test Measurements
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.2.7 based on the coefficient of variation of the mean TCP-value, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.2.8 based on values for that reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for t-z Method for Drilled Shafts in Weak Rock from Point Load Index Test Measurements
Settlement resistance factors to be applied to side resistance for shaft segments through weak rock shall be determined from Figure 751.37.4.2.9 based on the coefficient of variation of the mean Is(50)-value, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean uniaxial compressive strength for the rock over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on weak rock shall similarly be determined from Figure 751.37.4.2.10 based on values for that reflect the variability of the mean uniaxial compressive strength for the rock over the distance 2Ds below the tip of the shaft.
Settlement Resistance Factors for t-z Method for Drilled Shafts in Cohesive Soils
Settlement resistance factors to be applied to side resistance for shaft segments through cohesive soil shall be determined from Figure 751.37.4.2.11 based on the coefficient of variation of the mean undrained shear strength, . Values for shall be determined in accordance with EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation to reflect the variability of the mean undrained shear strength for the soil over the shaft segment. Settlement resistance factors to be applied to tip resistance for shafts founded on cohesive soil shall similarly be determined from Figure 751.37.4.2.12 based on values for that reflect the variability of the mean undrained shear strength for the soil over the distance 2D below the tip of the shaft.
For shafts founded in soft cohesive soils, consideration shall also be given to including additional settlement induced from time dependent consolidation of the soil.
Settlement Resistance Factors for t-z Method for Drilled Shafts in Cohesionless Soils
Settlement evaluations for individual drilled shafts in cohesionless soils shall be designed according to applicable sections of the current AASHTO LRFD Bridge Design Specifications.
751.37.4.3 Settlement of Drilled Shafts in Groups
| Commentary on EPG 751.37.4.3 Settlement of Drilled Shafts in Groups |
Settlement of Shaft Groups in Cohesive Soils
Settlement of shaft groups in cohesive soils shall be estimated according to EPG 751.38.4.3 using the “equivalent footing” approach described in LRFD 10.7.2.3.
Settlement of Shaft Groups in Cohesionless Soils Using Standard Penetration Test Measurements
Settlement for drilled shaft groups in cohesionless soils can be estimated from SPT measurements as
| (inches) | Equation 751.37.4.10 |
where:
- ρ = settlement of shaft group (inches),
- q = net foundation pressure applied at depth of D'(ksf),
- B = width or smallest dimension of shaft group (feet),
- I = 1 - 0.125(D'/B) ≥ 0.5 = influence factor of the effective group embedment (dimensionless),
- (N1)60 = SPT blow count corrected for overburden stress and hammer efficiency (blows/foot),
- D = 2Db/3 = effective depth of “equivalent footing” and
- Db = depth of embedment of shafts in layer that provides support.
The value for (N1)60 is determined as
| (blows/foot) | Equation 751.37.4.11 |
where:
- CN = = correction factor to account for overburden stress (dimensionless),
- ER = hammer efficiency expressed as percentage of theoretical free fall energy for hammer system actually used (percent) and
- N = uncorrected SPT blow count (blows/foot).
Settlement of Shaft Groups in Cohesionless Soils Using Cone Penetration Test Measurements
Settlement for drilled shaft groups in cohesionless soils can be estimated from CPT measurements as
| (inches) | Equation 751.37.4.12 |
where:
- ρ = settlement of shaft group (inches),
- q = net foundation pressure applied at depth of D'(ksf),
- B = width or smallest dimension of shaft group (feet),
- I = 1 - 0.125(D'/B) ≥ 0.5 = influence factor of the effective group embedment (dimensionless),
- qc = static cone tip resistance (ksf),
- D = 2Db/3 = effective depth of “equivalent footing” and
- Db = depth of embedment of shafts in layer that provides support.
Settlement of Shaft Groups in Rock
Settlement of shaft groups in rock shall be estimated according to EPG 751.38.4.2 using the “equivalent footing” approach described in LRFD 10.7.2.3.
751.37.5 Design for Lateral Loading at Strength and Service Limit States
| Commentary on EPG 751.37.5 Design for Lateral Loading at Strength and Service Limit States |
The Strength Limit State and applicable Extreme Event Limit States shall be investigated when calculating the soil and structural resistance of the drilled shaft for lateral loading. The Service I Limit State shall be used when evaluating lateral deflection.
Design lateral movements should not exceed approximately 1.5 in. at the top of the shaft at the Service I Limit State.
To analyze laterally loaded drilled shafts, the point of fixity of the drilled shaft must be estimated. This location may be estimated by using a computer program. This is an iterative process that requires first assuming a point of fixity so that the bent stiffness may be calculated. The stiffness of the bent may be found by modeling the bent in a structural analysis program, applying a load to the middle of the beam cap and measuring the amount of deflection caused by the load. The method shown in EPG 751.2.4.6 Loads - Longitudinal Wind Force Distribution and EPG 751.2.4.7 Loads - Longitudinal Temperature Force Distribution for modeling the stiffness, E'I, of a cast in place (C.I.P.) pile may also be used to model a drilled shaft. The moment of inertia of the bent is then found by:
| (consistent units of length4) | Equation 751.37.5.1 |
where:
- I = moment of inertia for the bridge bent (consistent units of length4),
- P = load applied to the middle of the beam cap (consistent units of force),
- L = length from point of fixity of shaft to middle of beam cap (consistent units of length),
- δ = deflection caused by load P (consistent units of length) and
- E = modulus of elasticity of concrete (consistent units of stress).
The E and I values used in the above equation shall also be used for longitudinal force distribution calculations.
The longitudinal forces applied to the bent can be calculated once the moment of inertia of the bent is known. Once loads are obtained, they can be input into computer software to get a point of fixity.
If the point of fixity is different than what was assumed to obtain the original bent stiffness, the bent stiffness shall be re-calculated with a new assumed point of fixity and this process continued until the point of fixity converges. As a rule of thumb, shafts socketed into rock are usually fixed near to the soil-rock interface.
The location of the point of fixity should be considered to be only an approximation. Many factors influence the actual location of the point of fixity. The thickness of the casing, scour and actual geotechnical properties could cause different results for the actual location of the point of fixity.
751.37.6 Structural Resistance of Drilled Shafts
| Commentary on EPG 751.37.6 Structural Resistance of Drilled Shafts |
751.37.6.1 Reinforcement Design
Drilled shaft structural resistance shall be designed similarly to reinforced concrete columns. The Strength Limit State and applicable Extreme Event Limit State load combinations shall be used in the reinforcement design.
Longitudinal reinforcing steel shall extend below the point of fixity of the drilled shaft at least 10 ft. in accordance with LRFD 10.8.3.9.3 or the required bar development length whichever is larger.
If permanent casing is used, and the shell consists of smooth pipe greater than 0.12 in. thick, it may be considered load carrying. An 1/8" shall be subtracted off of the shell thickness to account for corrosion. Casing could also be corrugated metal pipe. If casing is assumed to contribute to the structural resistance, the plans should indicate the minimum thickness and type of casing required.
Minimum clear spacing between longitudinal bars as well as between transverse bars shall not be less than five times the maximum aggregate size or 5 in. (LRFD 10.8.3.9.3).
For minimum concrete cover for drilled shaft, see Sec 701.4.12.1. If drilled shaft diameter does not match Sec 701.4.12.1 then use concrete cover for the next greater diameter drilled shaft. For rock sockets use 3” min. clear cover.
For longitudinal reinforcement, splicing shall be in accordance with LRFD 5.10.8.4.
For transverse reinforcement, lap splices for closed circular stirrups/ties shall be provided and staggered in accordance with LRFD 5.10.4.3. Lap length of 1.3 ld (Class B) for closed stirrups/ties shall be provided in accordance with LRFD 5.10.8.2.6d.
For lap length, see EPG 751.5.9.2.8.1 Development and Lap Splice General.
751.37.6.2 Longitudinal Reinforcement
Longitudinal reinforcement shall be designed to resist bending in the shaft due to lateral loads. The cross-sectional area for longitudinal reinforcement shall fall within the following limits:
| (consistent units of stress) | Equation 751.37.6.1 | |
| LRFD 5.7.4.2 |
where:
- Ag = gross cross-sectional area of drilled shaft (consistent units of area),
- f'c = concrete compressive strength (consistent units of stress),
- fy = yield strength of steel reinforcement (consistent units of stress) and
- Asteel = cross-sectional area of longitudinal steel reinforcement (consistent units of area).
MoDOT prefers to follow LRFD 5.7.4.2 for drilled shafts since for typical cases, the potential exists for load transfer between the concrete and steel casing. (The minimum area of reinforcement based on LRFD is 10 percent less than ACI for f’c = 4 ksi).
751.37.6.3 Factored Axial Resistance
The factored axial resistance of a drilled shaft shall be determined as
| (consistent units of force) | Equation 751.37.6.2 |
where:
- PR = factored axial resistance of drilled shaft (consistent units of force),
- PN = nominal axial resistance of drilled shaft (consistent units of force),
- = 0.75 = resistance factor for axial resistance of drilled shaft (dimensionless) and
- = factored axial load (consistent units of force).
For shafts with spiral reinforcement, the nominal axial resistance shall be computed as
| (consistent units of force) | Equation 751.37.6.3 |
where:
- Ag = gross cross-sectional area of drilled shaft (consistent units of area),
- f'c = concrete compressive strength (consistent units of stress),
- fy = yield strength of steel reinforcement (consistent units of stress) and
- Asteel = cross-sectional area of longitudinal steel reinforcement (consistent units of area).
For shafts with tie reinforcement, the nominal axial resistance shall be computed as
| (consistent units of force) | Equation 751.37.6.4 |
where:
- Ag = gross cross-sectional area of drilled shaft (consistent units of area),
- f'c = concrete compressive strength (consistent units of stress),
- fy = yield strength of steel reinforcement (consistent units of stress) and
- Asteel = cross-sectional area of longitudinal steel reinforcement (consistent units of area).
751.37.6.4 Transverse Reinforcement
Minimum transverse reinforcement shall be designed to resist the potential of diagonal cracking and improve ductility, and to control the stability of the reinforcement cage. Follow the four-step procedure, below:
No. 1. Determine if Transverse Reinforcement is Required for Loading
- If
| , | then go to No. 2a, below, otherwise, go to No. 2b. |
(consistent units of force) (LRFD 5.8.2.4) | Equation 751.37.6.4.1 |
- where:
- Vu = factored shear force (consistent units of force),
- = approximate shear resistance of drilled shaft (consistent units of force),
- Φ = 0.9 = resistance factor for shear resistance of drilled shaft (dimensionless),
- β = 2.0,
- bv = D = shaft diameter (consistent units of length),
- dv = 0.9 (D/2 + Dr /π) and
- Dr = diameter of circle passing through the centers of the longitudinal reinforcement (consistent units of length). See commentary for LRFD C5.8.2.9-2.
No. 2. Determine Minimum Transverse Reinforcement
- a) Minimum transverse reinforcement to control shear diagonal cracking and increase ductility:
- The minimum amount of transverse reinforcement shall satisfy the following equation if transverse reinforcement is required for loading in No. 1, otherwise go to No. 2b:
| (consistent units) | (LRFD 5.8.2.5) | Equation 751.37.6.4.2 |
- where:
- Av = area of transverse reinforcement within distance s (consistent units of area),
- s = spacing of transverse reinforcement (consistent units of length),
- bv = D = shaft diameter (consistent units of length),
- f'c = concrete compressive strength (consistent units of stress) and
- fy = yield strength of steel reinforcement (consistent units of stress).
- b) Minimum transverse reinforcement to control stability of cage before and during placement:
- Use minimum #4 @ 12” stirrups for reinforcing cage ≤ 4 ft. diameter and minimum #5 @ 12” stirrups for reinforcing cage > 4 ft. diameter (FHWA-NHI-10-016) unless transverse reinforcement needs to be designed as in No. 1. If transverse reinforcement needs to be designed as in No. 1, then provide the controlling transverse reinforcement area required by EPG 751.37.6.4 No. 2a, 2b and EPG 751.37.6.5 Factored Shear Resistance.
- All shafts, cased or uncased, or where casing is used for strength, shall be transversely reinforced.
No. 3. Determine Maximum Transverse Reinforcement Spacing:
- The maximum transverse reinforcement spacing shall be ≤ 12” to provide crack control without consideration for casing. MoDOT does not implement LRFD 5.8.2.7 maximum spacing of transverse reinforcement requirements for typical shaft sizes. However, for small shafts where LRFD 5.8.2.7 will control, it should be directly implemented.
No. 4. Determine Maximum Transverse Shaft Reinforcement Spacing at the Anchorage of Column Reinforcement:
- For columns with longitudinal reinforcement anchored into oversized shafts, in the anchorage region, the spacing of the transverse shaft reinforcement shall meet the requirements of the following equation:
| (consistent units) | (LRFD 5.11.5.2.1-1) | Equation 751.37.6.4.3 |
- where:
- Smax = maximum spacing of transverse shaft reinforcement (consistent units of length),
- Asp = area of transverse shaft reinforcement (consistent units of area),
- fytr = yield strength of transverse shaft reinforcement (consistent units of stress),
- ℓs = required lap splice of the longitudinal column reinforcement (consistent units of length),
- k = ratio of column tensile reinforcement to total column reinforcement at the nominal resistance,
- Aℓ = area of longitudinal column reinforcement (consistent units of area), and
- fuℓ = tensile strength of longitudinal column reinforcement (consistent units of stress).
751.37.6.5 Factored Shear Resistance
The factored shear resistance of a drilled shaft shall be determined as:
| (consistent units of force) | Equation 751.37.6.4.4 |
where:
- VR = factored shear resistance of drilled shaft (consistent units of force),
- Vc= nominal shear resistance from concrete (consistent units of force),
- Vs = = shear resistance from transverse shear reinforcement. (For Av, use transverse reinforcement area from EPG 751.37.6.4 Transverse Reinforcement and increase reinforcement area as needed to meet design requirements. (consistent units of force),
- Φ = 0.9 = resistance factor for shear resistance of drilled shaft (dimensionless),
- Av = area of transverse shear reinforcement within distance s (consistent units of area),
- fy = yield strength of steel reinforcement (consistent units of stress),
- θ = 45° = angle of inclination of diagonal compressive stresses (degrees),
- dv = 0.9 (D/2 + Dr /π) and
- Dr = diameter of circle passing through the centers of the longitudinal reinforcement (consistent units of length). See commentary for LRFD C5.8.2.9-2.
751.37.7 References
| Commentary on EPG 751.37.7 References |
AASHTO (2009), AASHTO LRFD Bridge Design Specification: Customary U.S. Units, American Association of State Highway and Transportation Officials, Fourth Edition with 2008 and 2009 Interim Revisions.
Hoek, E., and E.T. Brown (1988), “The Hoek-Brown Failure Criterion – A 1988 Update,” Proceedings of the 15th Canadian Rock Mechanics Symposium, Toronto, Canada.
Hoek, E., C. Carranza-Torres, and B. Corkum (2002), “Hoek and Brown Failure Criterion – 2002 Edition,” Proceedings of NARMS-TAC Conference, Toronto, Canada.
Horvath, R.G., and T.C. Kenney (1979), “Shaft Resistance of Rock Socketed Drilled Piers,” Proceedings of the Symposium on Deep Foundations, ASCE, pp. 182-214.
Loehr, J.E., B.L. Rosenblad, and T.T. Vu (2011a), MoDOT Transportation Geotechnics Research Program: Drilled Shaft Axial Load Test Program Interpretation Report, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Loehr, J.E., S.A. Grant, and B.L. Rosenblad (2011b), Calibration of Resistance Factors for Design of Drilled Shafts at Strength Limit States Using Laboratory Test Measurements, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
O’Neill, M.W., and L.C. Reese (1999), Drilled Shafts: Construction Procedures and Design Methods, Report No. FHWA-IF-99-025, Federal Highway Administration, McLean, VA, 758 pp.
Pierce, M.D., J.E. Loehr, and B.L. Rosenblad (2011), Calibration of LRFD Resistance Factors for Design of Drilled Shafts at Strength Limit States Using In situ Test Measurements, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Reese, L.C., W.M. Isenhower, and S-T Wang (2006), Analysis and Design of Shallow and Deep Foundations, John Wiley and Sons, 574 pp.
Wyllie, D.C. (1999), Foundations on Rock, E & FN Spon, Second Edition, 401 pp.
751.37.8 Commentary
Commentary on EPG 751.37.1 General
These guidelines were developed from prior EPG guidelines with notable changes to the general approach for application of LRFD techniques as well as updated resistance factors based on probabilistic calibrations. Calibration analyses were performed following generally accepted procedures for calibration of resistance factors for geotechnical applications, but with modifications to permit several enhancements to be implemented. The most notable enhancements provided in the guidelines include:
- Use of resistance factors that are dependent upon the variability and uncertainty that exists in select design properties
- Adoption of different target reliability levels for foundations of structures of different operational importance.
Both of these enhancements are expected to produce efficient foundation designs while still maintaining appropriate safety and reliability for all classes of operational importance. Additional information regarding development of the methods provided in these guidelines can be found in Loehr et al. (2011b), Pierce et al. (2011), and Vu and Loehr (2011). Additional information regarding target reliability values established for different classes of operational importance is provided in Bowders et al. (2011).
The four classes of operational importance include:
- Minor or low volume route
- Major route
- Major bridge costing less than $100 million
- Major bridge costing greater than $100 million.
These classifications are based on common MoDOT designations. The target reliability levels established for each limit state and operational importance were generally based upon consideration of highway bridges. However, the methods provided in this article can also be utilized for design of foundations for other structures including retaining walls and roadway signs.
Calibration analyses performed to establish the resistance factors presented in these guidelines were performed using the latest knowledge of variability and uncertainty in applied loads (Kulicki et al., 2007), as well as using load factors that are currently in effect. The resistance factors provided in these guidelines are intended to produce foundations with reliabilities that are approximately equal to the target reliabilities established by MoDOT when utilized with current load factors. Since it is the combined effect of load and resistance factors that produce this reliability, the resistance factors provided are inherently coupled with current load factors and are contingent upon the uncertainty and variability in the applied loads that were presumed for the calibrations. As such, recalibration of resistance factors is required if alternative load factors are adopted, or if substantial revisions to current estimates of load variability and uncertainty are found.
It is important to emphasize that the resistance factors provided in these guidelines were developed presuming that mean values would be used for all design parameters in the methods provided. This departs from past practice utilizing allowable stress design (ASD) approaches where nominal values of parameters that were less than mean values were often used to introduce conservatism into the analyses beyond that provided by the ASD factor of safety. Use of design parameters less than the mean values within the context of these guidelines will often, but not always, increase the reliability of foundation designs; however, such practice is contrary to the spirit of LRFD in that it will not produce foundations that achieve the target reliability established by MoDOT policy.
The procedures provided in these guidelines are not intended as a substitute for good judgment. Rather, the intent of these guidelines is to:
- 1) inform designers of generally appropriate levels of conservatism to address the variability and uncertainty involved in different aspects of design analyses and
- 2) provide quantitative methods to achieve target reliabilities for foundations depending on the variability and uncertainty present in relevant design parameters and design methods.
Designers must still use their best judgment in considering design options (e.g. foundation depth, type and size; necessity for load tests; etc.) for establishing the most appropriate foundations for bridges and other structures.
Design methods provided in these guidelines are mostly empirical methods derived from results of full-scale load tests. Application of these methods is generally restricted to geologic conditions and construction procedures similar to those represented by the load tests used to establish the methods. In particular, methods presented for prediction of nominal and factored shaft resistance in weak rock were specifically developed from load tests performed in Missouri following established MoDOT construction specifications. As such, these methods are, strictly speaking, only applicable to cases where shafts will be constructed in general accordance with current MoDOT construction specifications. Use of these guidelines for conditions or situations that depart from these restrictions is permissible, but requires that designers give consideration to the effects of differences between the specific site conditions encountered and those represented by the empirical data.
Commentary on EPG 751.37.1.1 Dimensions and Nomenclature
The length to diameter ratio of drilled shafts should generally be targeted for the range 3 ≤ L/D ≤ 30; however, shafts with dimensions falling outside of this range can, at times, be effectively utilized.
Commentary on EPG 751.37.1.2 Materials
Where possible, the concrete mix for drilled shafts should utilize MoDOT aggregate gradation E (1/2 inch minus) to improve the workability of the concrete during placement and reduce the risk of shaft defects. Special attention should also be given to concrete slump requirements to ensure the concrete has sufficient workability to completely surround the reinforcing cage without vibration. For cases where “tight cages” are required, consideration should be given to using special construction provisions to minimize the risk of concrete placement problems.
Commentary on EPG 751.37.1.3 Casing
Temporary or permanent casing is commonly required to support the shaft excavation during construction to prevent caving of overburden soils. Use of permanent casing generally simplifies construction by avoiding the need for multiple cranes to simultaneously place concrete and extract the casing and reduces the risk of problems during concrete placement. However, use of either temporary or permanent casing will generally reduce the side resistance of the constructed shaft over the cased length. Alternatives to use of casing include use of mineral or polymer slurry to maintain the stability of the excavation during construction, or use of no casing and no slurry when soil/rock conditions will permit the shafts to be constructed without caving of the excavation walls.
Permanent casing may also be required to provide structural resistance, especially when lateral loads are substantial (see EPG 751.37.6). For example, permanent casing may be required to:
- Achieve the required flexural resistance of the drilled shaft
- Resist large lateral loads for bridges located in seismic areas
- Facilitate shaft construction through water
- Support the shaft excavation when there is insufficient head room available for casing recovery
Commentary on EPG 751.37.1.4 General Design Considerations
Scour
Appropriate methods for evaluation of scour are beyond the scope of these guidelines. However, these guidelines require that drilled shafts be designed to acceptably support the structure assuming that the foundation soil/rock is scoured to depths predicted following currently accepted practice.
Downdrag
Downdrag loads should be considered any time settlement is likely to occur in soils surrounding drilled shafts. Downdrag is most commonly a concern for foundations passing through or near to approach fills overlying soft, cohesive soils where the applied load of the fill will induce settlement in the underlying soft soils. Downdrag is seldom a concern for intermediate bents away from approach fills (because there is often no loading to induce compression of the soft soils) unless settlement is likely to be induced by lowering groundwater levels.
Downdrag loads are generally fully mobilized with relatively small settlements and can be substantial. In cases where downdrag loading is significant, consideration should be given to staging construction of shafts, if timing will allow, such that shafts are installed after settlement has practically ceased or to other techniques to limit the effects of downdrag.
Group Effects
The redundancy factor of LRFD 1.3.4 is not intended to account for redundancy or lack of redundancy in foundation design. The LRFD redundancy factor, ηR, has been a source of confusion for foundation design, especially given that group efficiency factors are also denoted as η. Use of the redundancy factor to account for the presence or absence of redundancy in the foundations is inappropriate as this factor was developed purely from considerations of the performance of the superstructure and not the foundations as discussed in LRFD C10.5.5.2.4.
Commentary on EPG 751.37.1.5 Related Provisions
Use of site characterization practices that significantly depart from those currently used by MoDOT can produce substantial differences in design parameters and/or the variability of design parameters, which will lead to substantial differences in foundation reliability and failure to achieve the established target foundation reliabilities established by MoDOT. Use of the methods in these guidelines is generally restricted to design parameters established following current MoDOT site characterization practices as described in EPG 321.
Commentary on EPG 751.37.2 General Design Procedure and Limit States
Selection of applicable strength and serviceability limit states shall be accomplished in close consultation with the Structural Project Manager. At a minimum, the Strength I and Service I limit states should be evaluated. When multiple strength and/or service limit states are considered, the limit state producing the greatest minimum shaft dimensions shall govern the final design dimensions.
Axial geotechnical resistance will frequently control the dimensions of drilled shafts. However, lateral strength or serviceability may dictate final shaft dimensions when shafts are subjected to large lateral loads.
Note that it is possible that a shaft can be shortened from that initially determined considering only axial loads. This can occur where a shaft’s diameter must be increased to satisfy lateral strength or serviceability requirements (e.g. to increase bending/shear strength/stiffness). When this occurs, designers should revisit the relevant axial strength and axial serviceability requirements to evaluate whether a shaft of the diameter required to meet lateral serviceability requirements can be made shorter than what was originally determined for a smaller diameter shaft. One should not simply increase the diameter to satisfy the lateral loading requirements without reconsidering the shaft length. Often multiple combinations of shaft diameter and length can be made to satisfy the axial loading requirements.
Lengths of rock sockets should generally be limited to the extent possible because rock sockets commonly have substantially higher unit costs.
Commentary on EPG 751.37.3 Geotechnical Resistance for Axial Loading at Strength Limit States
Throughout EPG 751.37, factored loads are denoted as . This notation should not be taken to suggest inclusion or exclusion of specific load effects, but rather is simply intended as a convenient notation to reflect factored loads. When applying these guidelines, designers should replace with load combinations and load factors that are appropriate for the structure and limit state being considered.
Side resistance over the cased length of shaft is commonly neglected for rock-socketed shafts because the resistance is difficult to appropriately establish and because the resistance generally contributes little to the overall shaft resistance. For shafts founded exclusively in soil, the potential resistance over the cased length may provide a more substantial contribution to resistance.
Judgment should be applied when deciding whether to ignore tip resistance in karstic formations including consideration of the prevalence of voids and likelihood of encountering them during actual construction. Consideration should also be given to use of special provisions that stipulate appropriate action if voids are encountered in verification holes.
Design procedures within this article are categorized according to material type, including methods for design of shafts founded within “rock”, “weak rock”, “cohesive soil”, and “cohesionless soil”. While these categories serve to logically separate the guidelines according to design method, complexities present at some sites may lead to cases where multiple methods could potentially be used. In such cases, designers should utilize the method that is most appropriate for the conditions encountered, rather than selecting the method that produces the smallest or largest shaft dimensions.
EPG 751.37.3.1 is generally intended for use with “harder” rock materials where the frequency, orientation, and condition of rock discontinuities tend to dominate the response of the rock to loading from foundations. Such rock masses will generally be composed of rock with uniaxial compressive strengths that are greater than 100 ksf, although some exceptions to this limit could arise. Limestones and dolomites will commonly fall under this article as will many sandstones, and even a few hard shales.
EPG 751.37.3.2, EPG 751.37.3.3, EPG 751.37.3.4, and EPG 751.37.3.5 are intended for use with weaker rock where the properties of the intact rock tend to dominate performance. These articles represent alternative means for design in shales, some weak sandstones, and potentially some very stiff clays. Several alternative methods are provided because of difficulties that can arise with reliable sampling and testing of weak rock. EPG 751.37.3.2 is intended for use when the compressive strength of the rock is determined using conventional uniaxial compression tests whereas the remaining articles provide means for designing drilled shafts in weak rock based on in situ tests or index tests. Use of methods provided in these articles for materials with properties falling outside of the measurement bounds provided should be done with extreme caution as the methods may dramatically overestimate the resistance that can be realistically achieved beyond the bounds provided.
EPG 751.37.3.6 and EPG 751.37.3.7 are intended for use with cohesive and cohesionless soils, respectively. Some overlap exists between the strength limits provided in EPG 751.37.3.2 and EPG 751.37.3.6 (Note that the limits for EPG 751.37.3.2 are based on the uniaxial compressive strength whereas the limits for EPG 751.37.3.6 are based on the undrained shear strength, which is nominally one half of the compressive strength). When designing for materials that fall within this overlapping range of strengths, designers shall use the method that is most appropriate for the material encountered.
Commentary on EPG 751.37.3.1 Axial Resistance for Individual Drilled Shafts in Rock (qu ≥ 100 ksf')
Commentary on Side Resistance for Drilled Shafts in Rock (qu ≥ 100 ksf')
The design method provided in this article is adapted from Horvath and Kenney (1979) based on evaluation of results from a small number of load tests performed in Missouri limestones for shafts constructed in general accordance with current MoDOT construction specifications. Analysis of this data shows that the “best fit” trend to the empirical data is similar to the Horvath and Kenny relationship.
The resistance factors provided in Figure 751.37.3.1.1 were established from probabilistic calibrations to achieve the target foundation reliabilities established by MoDOT as described in Loehr et al. (2011b). The variability and uncertainty present for dead load, live load, the uniaxial compressive strength of the rock, as well as the variability and uncertainty of the design method were explicitly considered in these calibrations. The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). The variability and uncertainty utilized for the design method were established from empirical data derived from load tests performed on test shafts constructed in general accordance with current MoDOT construction specifications. Consideration of additional load test results from test shafts not constructed following these specifications was found to lead to substantially lower required resistance factors. As such, the resistance factors provided are not generally appropriate for shafts constructed according to specifications that differ substantially from current MoDOT construction specifications.
The coefficient of variation for the mean uniaxial compressive strength used in Equation 751.37.3.4 shall reflect the variability and uncertainty in the mean compressive strength rather than the variability and uncertainty in measurements of compressive strength as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed on samples taken from within the depth range of the shaft segment being considered. However, the values used should reflect the mean and variability in the material parameters within that depth range.
Commentary on Tip Resistance for Drilled Shafts in Rock (qu ≥ 100 ksf')
The design method provided in this article is adapted from the method presented in Wyllie (1999) to conform to the LRFD approach. The method is derived from the Hoek-Brown strength criterion (Hoek and Brown, 1988) that is commonly used to represent the strength of fractured rock masses using the rock mass parameters, m and s. The resistance factors provided in Figure 751.37.3.1.2 were established from probabilistic calibrations to achieve the target foundation reliabilities as described in Abu El-Ela et al. (2011) and are identical to those provided in EPG 751.38.3.1 for bearing resistance of spread footings on fractured rock. These calibrations were conducted with explicit consideration of variability and uncertainty present for dead load, live load, uniaxial compressive strength, and the design method itself (i.e. a “method” uncertainty). The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). The variability and uncertainty in the design method was conservatively estimated utilizing the likely range of m and s values expected for a particular condition.
Unfortunately, empirical data to evaluate design methods for predicting the ultimate tip resistance of drilled shafts in fractured rock are not presently available. As such, the variability and uncertainty attributed to the design method was conservatively estimated as a matter of prudence. One consequence of this conservatism is that the factored tip resistance predicted for foundations designed according to EPG 751.37.3.1 may, in some cases, be less than the factored tip resistance predicted according to EPG 751.37.3.2 for rock that might be considered to have lower quality. This consequence is a reflection of the lack of data available to confirm the predicted resistance using the prescribed method, and thus the limited reliability of the method, rather than an indication that the tip resistance will actually be less than that for lesser rock. Future research to measure the ultimate tip resistance for drilled shafts in fractured rock could dramatically improve the accuracy and reliability of these methods, which in turn would dramatically improve the efficiency of foundation designs for fractured rock. This consequence also suggests that site specific load tests could potentially improve foundation efficiency in some cases while still maintaining the target reliability.
The coefficient of variation for the mean uniaxial compressive strength used in Equation 751.37.3.5 shall reflect the variability and uncertainty in the mean compressive strength rather than the variability and uncertainty in measurements of compressive strength as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for , , m and s do not have to be established exclusively from tests or observations performed for rock specimens taken from within the depth range of interest below the tip of the shaft. However, the values used should reflect the mean and variability in the material parameters within that depth range.
Several methods are available for establishing appropriate values of GSI for specific rock masses. Equation 751.37.3.8 represents a generally rigorous approach for determination of GSI that should be used when available measurements and observations allow for establishing Rock Mass Rating system ratings and when these ratings produce RMR greater than 25. In cases where such measurements and observations are not available, or where RMR is less than 25, GSI values can be estimated using the qualitative chart shown in Fig. Commentary 751.37.3.1.1 based on the work of Marinos and Hoek (2000). Figs. Commentary 751.37.3.1.2, Commentary 751.37.3.1.3 and Commentary 751.37.3.1.4 provide additional guidance for qualitative selection of GSI for typical sandstones, shales and limestones from the chart.
In cases where GSI cannot be rationally determined, it is also possible to directly estimate approximate values for the rock mass parameters m and s from Table Commentary 751.37.3.1 using qualitative descriptions of the rock mass. The values provided in Table Commentary 751.37.3.1 will generally be less than values that will be produced using Equations 751.37.3.6 and 751.37.3.7. This result is because the values in Table Commentary 751.37.3.1 were established under the assumption that excavation-induced damage will occur (i.e. that the Hoek and Brown damage factor, D, is equal to 1) while Equations 751.37.3.6 and 751.37.3.7 were established assuming that no significant excavation-induced damage will occur (i.e. that D = 0). Since significant excavation-induced damage is unlikely to occur for shafts excavated using conventional construction techniques, the values provided in Table Commentary 751.37.3.1 will be conservative. It is also important to point out that m and s can be roughly interpolated from the values provided in Table Commentary 751.37.3.1 for conditions falling between those listed.
Methods provided in this subarticle are not appropriate for use with uniaxial compressive strengths estimated from Point Load Index tests or from other empirical correlations. Use of correlations for estimation of uniaxial compressive strength introduces additional variability into the relation among rock mass parameters, uniaxial compressive strength, and side and tip resistance that is not accounted for in the resistance factors provided. Use of compressive strengths derived from Point Load Index values or other correlations is therefore not appropriate for application of the provisions of this subarticle. It is possible to develop resistance factors that would be appropriate for such use, but such calibrations have not been completed at this time.
Commentary on EPG 751.37.3.2 Axial Resistance for Individual Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)
Several alternative methods are provided to estimate side resistance for shafts founded in weak rock. Any of these alternatives may be used depending upon the site characterization data that are available. All methods provided are intended to produce shafts with reliabilities that are approximately equal to the established target reliability for the operational importance utilized. However, the methods will not necessarily produce shafts with identical dimensions so designers are encouraged to consider potential efficiencies that can be realized from utilization of the alternative methods. It is currently anticipated that methods in EPG 751.37.3.2 will produce the most cost-effective drilled shafts from among the methods provided. However, additional experience with the different provisions is needed to confirm this belief.
The design methods provided in this article were established from analysis of data from load tests performed in weak rock at sites in Missouri as described in Rosenblad et al. (2011), Loehr et al. (2011a), and Miller (2003). The resistance factors provided in Figures 751.37.3.1.3 and 751.37.3.1.4 were established from probabilistic calibrations to achieve established target reliabilities as described in Loehr et al. (2011b). The variability and uncertainty present for dead load, live load, and uniaxial compressive strength were explicitly considered in these calibrations, in addition to variability and uncertainty associated with the empirical design method itself. The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). Variability and uncertainty for the empirical design method were established from statistical analysis of the empirical data as described in Loehr et al. (2011b).
Uniaxial compressive strengths established from Point Load Index tests or from other empirical correlations are not appropriate for use with the methods provided in this subarticle. Use of correlations for estimation of uniaxial compressive strength introduces additional variability and uncertainty into the relations among uniaxial compressive strength and side and tip resistance that is not accounted for in the resistance factors provided. Use of compressive strengths derived from Point Load Index values or other correlations is therefore not appropriate for application of the provisions of this subarticle. Methods provided in EPG 751.37.3.5 shall be used to design drilled shafts using results from Point Load Index tests.
Commentary on Side Resistance for Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤100 ksf)
The coefficient of variation for the mean uniaxial compressive strength used in Equation 751.37.3.9 shall reflect the variability and uncertainty in the mean compressive strength rather than the variability and uncertainty in measurements of compressive strength as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed on samples taken from the depth range of the shaft segment. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit side resistance provided in Equation 751.37.3.9 is limited to be less than 30 ksf because predictions resulting from use of the equation for qu ≥ 100 ksf will often exceed what can be reliably mobilized for large uniaxial compressive strengths.
Commentary on Tip Resistance for Drilled Shafts in Weak Rock from Uniaxial Compression Tests on Rock Core (5 ksf ≤ qu ≤ 100 ksf)
The coefficient of variation for the mean uniaxial compressive strength used in Equation 751.37.3.10 shall reflect the variability and uncertainty in the mean compressive strength rather than the variability and uncertainty in measurements of compressive strength as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed on samples taken from within the depth range of interest below the tip of the shaft. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit tip resistance provided in Equation 751.37.3.10 is limited to be less than 400 ksf because predictions resulting from use of the equation for qu ≥ 100 ksf will often exceed what can be reliably mobilized for large uniaxial compressive strengths.
Commentary on EPG 751.37.3.3 Axial Resistance for Individual Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
The design methods provided in this article were established from analysis of data from load tests performed in weak rock at sites in Missouri as described in Rosenblad et al. (2011), Loehr et al. (2011a), Pierce et al. (2011), and Miller (2003). The resistance factors provided in Figures 751.37.3.5 and 751.37.3.6 were established from probabilistic calibrations to achieve established target reliabilities as described in Pierce et al. (2011). The variability and uncertainty present for dead load, live load, and equivalent SPT N-value were explicitly considered in the calibrations, in addition to variability and uncertainty associated with the empirical design method itself. The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). The variability and uncertainty for the empirical design method was established from statistical analysis of the empirical data as described in Pierce et al. (2011).
“Equivalent N-value” is used in these guidelines because, strictly speaking, the value used is not a true SPT N-value. Common practice is to limit the number of hammer blows in SPT measurements to approximately 50 blows in 6 inches (depending upon the energy rating of the hammer). As such, N-values greater than 100 blows per foot are not reported. Rather, when tests fail to penetrate at least 6 inches, the penetration achieved for 50 blows is reported to reflect the relative strength and stiffness of the test material. In such cases, the “equivalent” N-value is calculated as
| (dimensionless) | Equation Commentary 751.37.3.1 |
where:
- Neq = “equivalent SPT N-value” (blows/foot),
- b = number of blows applied (blows) and
- p = measured penetration of Standard sampler (inches).
When tests successfully penetrate 6 in. during one testing increment but subsequently fail to penetrate 6 in. during a successive increment, the equivalent N-value shall be computed using the combined number of blows and combined penetration of both testing increments. While Neq is not strictly an SPT N-value, its use is consistent with current MoDOT practice and, since it was used as the basis for calibration of the methods of this article, is appropriate for use in design.
Commentary on Side Resistance for Drilled Shafts in Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
The coefficient of variation for the mean equivalent SPT N-value used in Equation 751.37.3.11 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements of the equivalent N-value as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed over the depth range of the shaft segment. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit side resistance provided in Equation 751.37.3.11 is limited to be less than 30 ksf because predictions resulting from use of the equation for N_eq≥400 blows/foot will often exceed what can be reliably mobilized.
Commentary on Tip Resistance for Drilled Shafts Weak Rock from Standard Penetration Tests (Neq ≤ 400 blows/ft)
The coefficient of variation for the mean equivalent SPT N-value used in Equation 751.37.3.12 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements of the equivalent N-value as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed over the depth range of interest below the tip of the shaft. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit tip resistance provided in Equation 751.37.3.12 is limited to be less than 400 ksf because predictions resulting from use of the equation for Neq ≥ 400 blows/ft. will often exceed what can be reliably mobilized.
Commentary on EPG 751.37.3.4 Axial Resistance for Individual Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)
The design methods provided in this article were established from analysis of data from load tests performed in weak rock at sites in Missouri as described in Rosenblad et al. (2011), Loehr et al. (2011a), Pierce et al. (2011), and Miller (2003). The resistance factors provided in Figures 751.37.3.4.1 and 751.37.3.4.2 were established from probabilistic calibrations to achieve established target reliabilities as described in Pierce et al. (2011). The variability and uncertainty present for dead load, live load, and Texas Cone Penetration test penetration were considered in these calibrations, in addition to variability and uncertainty associated with the empirical design method itself. The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). The variability and uncertainty for the empirical design method was established from statistical analysis of the empirical data as described in Pierce et al. (2011).
Commentary on Side Resistance for Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤10 in.)
Resistance factors to produce the established target reliabilities from mean TCP values actually vary slightly depending on the magnitude of the mean TCP-value. However, since the differences observed in resistance factors were small, average values determined over the range of potential TCP-values (1 in. ≤ TCP ≤10 in.) were used as a practical simplification.
The coefficient of variation for the mean TCP-value used in Equation 751.37.3.13 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed over the depth range of the shaft segment. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit side resistance provided in Equation 751.37.3.13 is limited to be less than 30 ksf because predictions resulting from use of the equation for TCP ≥ 10 in. will often exceed what can be reliably mobilized.
Commentary on Tip Resistance for Drilled Shafts in Weak Rock from Texas Cone Penetration Tests (1 in. ≤ TCP ≤ 10 in.)
Resistance factors to produce the established target reliabilities from mean TCP values actually vary slightly depending on the magnitude of the mean TCP-value. However, since the differences observed in resistance factors were small, average values determined over the range of potential TCP-values (1 in. ≤ TCP ≤ 10 in.) were used as a practical simplification.
The coefficient of variation for the mean TCP-value used in Equation 751.37.3.14 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed over the depth range of interest below the tip of the shaft. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit tip resistance provided in Equation 751.37.3.14 is limited to be less than 400 ksf because predictions resulting from use of the equation for TCP ≥ 10 in. will often exceed what can be reliably mobilized.
Commentary on EPG 751.37.3.5 Axial Resistance for Individual Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
The design methods provided in this article were established from analysis of data from load tests performed in weak rock at sites in Missouri as described in Rosenblad et al. (2011), Loehr et al. (2011a), and Miller (2003). The resistance factors provided in Figures 751.37.3.5.1 and 751.37.3.5.2 were established from probabilistic calibrations to achieve established target reliabilities as described in Loehr et al. (2011b). The variability and uncertainty present for dead load, live load, and Point Load Index were explicitly considered in these calibrations, in addition to variability and uncertainty associated with the empirical design method itself. The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). Variability and uncertainty for the empirical design method were established from statistical analysis of the empirical data as described in Loehr et al. (2011b).
Commentary on Side Resistance for Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
The coefficient of variation for mean Point Load Index values used in Equation 751.37.3.15 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed on samples taken from the depth range of the shaft segment. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit side resistance provided in Equation 751.37.3.15 is limited to be less than 30 ksf because predictions resulting from use of the equation for ≥ 40 ksf will often exceed what can be reliably mobilized.
Commentary on Tip Resistance for Drilled Shafts in Weak Rock from Point Load Index Tests (5 ksf ≤ Is(50) ≤ 40 ksf)
The coefficient of variation for mean Point Load Index values used in Equation 751.37.3.16 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed on samples taken from the depth range of interest below the tip of the shaft. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The nominal unit tip resistance provided in Equation 751.37.3.16 is limited to be less than 400 ksf because predictions resulting from use of the equation for ≥ 40 ksf will often exceed what can be reliably mobilized.
Commentary on EPG 751.37.3.6 Axial Resistance for Individual Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
Commentary on Side Resistance for Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
The design method and resistance factors provided in this article were established from probabilistic calibrations performed using empirical data from Kulhawy and Jackson (1993) and analyses of variability by Phoon and Kulhawy (2005). Equation 751.37.3.18 was established from analysis of the data from Kulhawy and Jackson (1993), with curve fitting constraints to keep the relationship simple.
The resistance factors provided in this article should be considered approximate at this time for two reasons. The first reason is that the calibrations were performed using the variability of the measurements of unit side resistance, rather than the variability of predictions for unit side resistance. The result of this approximation is to generally underestimate the variability of unit side resistance and therefore to overestimate the resistance factors needed to achieve a given target reliability. This approximation is believed to be acceptable on an interim basis because the magnitude of the error is believed to be small since the data set is relatively large and the magnitude of this error decreases with the size of the data set. The second reason is that the empirical data upon which the resistance factors were derived were based on load tests performed on shafts that were not necessarily constructed following current MoDOT construction specifications. This does not necessarily mean that the results are not representative of results that would be obtained if the shafts were constructed following MoDOT specifications, but it does introduce some additional variability and uncertainty because the effect of construction methods is unknown. Such additional variability and uncertainty was not included in the calibrations performed to establish the resistance factors provided. MoDOT currently designs very few drilled shafts that derive substantial resistance from side shear in cohesive soils. However, more rigorous calibration of these resistance factors should nevertheless be performed to improve the precision of designs conducted using these provisions.
The resistance factors provided in this article are based on the assumption that measurements of undrained shear strength will accurately reflect the actual undrained shear strength in the field. Use of undrained shear strength values established from approximations or from index tests such as hand-held penetrometer tests, Torvane tests, or Standard Penetration Tests will introduce additional variability and uncertainty into the design that is currently not reflected in the resistance factors provided. As such, it is not generally appropriate to use such approximations for estimating undrained shear strength for use in these provisions. At a minimum, undrained shear strengths should be established based on unconfined compression tests performed on specimens acquired using good quality boring techniques and good quality “undisturbed” sampling with thin walled samplers. It is preferable to perform unconsolidated-undrained type triaxial tests or consolidated-undrained type triaxial tests to establish undrained shear strength values for use in these provisions.
The coefficient of variation for the mean undrained shear strength used in Equations 751.37.3.17 and 751.37.3.18 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed on samples taken from the depth range of interest below the tip of the shaft. However, the values used should reflect the mean and variability in the material parameters within that depth range.
Commentary on Tip Resistance for Drilled Shafts in Cohesive Soils (su ≤ 5 ksf)
The design method provided is currently unchanged from prior MoDOT guidance. Resistance factors provided in this article are revised from prior versions of the EPG. These resistance factors were established from probabilistic calibrations and are identical to those provided for bearing capacity of spread footings in cohesive soils in EPG 751.38.3.3.
The coefficient of variation for the mean undrained shear strength used in Equation 751.37.3.19 shall reflect the variability and uncertainty in the mean value rather than the variability and uncertainty in measurements as described in EPG 321.3 Procedures for Estimation of Geotechnical Parameter Values and Coefficients of Variation. Values for and do not have to be established exclusively from tests performed on samples taken from the depth range of interest below the tip of the shaft. However, the values used should reflect the mean and variability in the material parameters within that depth range.
The resistance factors provided in this article are based on the assumption that measurements of undrained shear strength will accurately reflect the actual undrained shear strength in the field. Use of undrained shear strength values established from approximations or from index tests such as hand-held penetrometer tests, Torvane tests, or Standard Penetration Tests will introduce additional variability and uncertainty into the design that is currently not reflected in the resistance factors provided. As such, it is not generally appropriate to use such approximations for estimating undrained shear strength for use in these provisions. At a minimum, undrained shear strengths should be established based on unconfined compression tests performed on specimens acquired using good quality boring techniques and good quality “undisturbed” sampling with thin walled samplers. It is preferable to perform unconsolidated-undrained type triaxial tests or consolidated-undrained type triaxial tests to establish undrained shear strength values for use in these provisions.
Commentary on EPG 751.37.3.7 Axial Resistance for Individual Drilled Shafts in Cohesionless Soils
Commentary on Side Resistance for Drilled Shafts in Cohesionless Soils
This subarticle is unchanged from prior versions of the EPG aside from minor editorial revisions. Probabilistic calibrations for drilled shafts in cohesionless soils have not been completed at this time.
Commentary on Tip Resistance for Drilled Shafts in Cohesionless Soils
This subarticle is unchanged from prior versions of the EPG aside from minor editorial revisions. Probabilistic calibrations for drilled shafts in cohesionless soils have not been completed at this time.
Commentary on EPG 751.37.3.8 Geotechnical Resistance from Load Tests
This subarticle is unchanged from prior versions of the EPG. Probabilistic calibrations for drilled shafts designs incorporating results from load tests have not been completed at this time. Additional study of available results for load tests in Missouri will likely lead to revision of appropriate resistance factors for use when load tests are performed.
Commentary on EPG 751.37.3.9 Evaluation of Group Effects
Two potential effects arise when drilled shafts are installed in groups with relatively close spacing. The first, and most commonly referenced effect is that there is potential for the cumulative resistance for all shafts in the group to be less than the sum of the individual shaft resistances. Such effects are commonly referred to as “group effects” in the geotechnical literature and have been traditionally accounted for using the methods provided in this article.
The second effect relates to the reliability of a group of shafts relative to the reliability of individual shafts. In general, the reliability of a group of drilled shafts will be greater than that of an individual shaft with the same resistance because groups benefit from “averaging” of shaft resistance, which tends to make their collective resistance more reliable than the resistance from an individual shaft. The resistance factors provided in these guidelines are those that produce the target foundation reliabilities for individual shafts. As such, use of these resistance factors for groups of shafts will tend to produce foundations that are more reliable than the established target reliabilities. No explicit account is made for this effect in the current guidelines, but designers should be aware of this issue. Additional study is needed to allow for this effect to be properly reflected in LRFD methods.
This also raises the issue of redundancy factors, generally denoted as ηR, in LRFD 1.3.4. The LRFD redundancy factor has been a source of confusion for foundation design, especially given that group efficiency factors are also denoted as η. Use of the redundancy factor to account for the presence or absence of redundancy in the foundations is inappropriate as this factor was developed purely from considerations of the performance of the superstructure and not the foundations as discussed in LRFD C10.5.5.2.4. LRFD 10.5.5.2.4 indicates that resistance factors provided in AASHTO (2009) should be reduced by 20 percent for non-redundant foundations to account for the lack of redundancy. Such reductions should not be applied to the resistance factors provided in these guidelines as the resistance factors were established considering the reliability of individual shafts. While one could conversely argue that the resistance factors provided in these guidelines should therefore be increased by 20 percent for redundant foundations, such a position does not seem justified without additional study and verification that such application is in fact appropriate.
When mixed soil profiles are present, the specific approach utilized for evaluation of group effects shall be based on the soil/rock type that provides the greatest contribution to resistance. For example, for a shaft group founded in rock overlain by cohesive soil, group effects shall be evaluated following the guidelines provided for rock since the shaft resistance will be predominantly derived from side resistance and tip resistance in the rock.
Commentary on Group Effects in Cohesionless Soils
The provisions provided in this article for cohesionless soils are drawn from the AASHTO LRFD Bridge Design Specification (AASHTO, 2009). Group efficiency factors for drilled shafts in cohesionless soils are generally less than one to account for potential loosening of the soil during shaft excavation and potential for overlapping stresses surrounding the shafts. This is contrary to what is observed for driven piles in most cohesionless soils, where group efficiency factors are commonly greater than one because of densification of the cohesionless soils during pile driving.
Commentary on Group Effects in Cohesive Soils
No probabilistic calibrations of the “equivalent pier” approach have been performed by MoDOT at this time. The resistance factor provided in this subarticle for evaluation of the equivalent pier is taken from the AASHTO LRFD Bridge Design Specification (AASHTO, 2009). The resistance factor for evaluation of the equivalent pier shall be applied to the total resistance of the equivalent pier (side resistance and tip resistance).
The resistance factors for summation of the individual shaft resistances shall be applied separately for side resistance and tip resistance based on the resistance factors provided in these guidelines for the appropriate soil/rock type(s).
Commentary on Group Effects in Rock
Few data are available to quantify group effects for shafts founded in rock or shafts founded in stratified soil/rock. The provisions provided for rock are based on considerable judgment drawn from discussions with a number of foundation designers and researchers.
Commentary on EPG 751.37.4 Design for Axial Loading at Serviceability Limit States
The provisions of this article were developed to limit foundation settlements to be less than generally tolerable levels of settlement with some target reliability. Target reliability levels for service limit states are substantially less than target reliability levels for strength limit states because the consequences associated with serviceability limit states are substantially less than consequences for strength limit state conditions. The ramification of these facts is that some foundations designed according to these guidelines may experience settlements that exceed tolerable settlements in some instances. The frequency of foundations settling more than tolerable limits should approach the established target probabilities of exceedance when considered over a large number of projects. In cases where actual foundation settlements are observed to exceed tolerable limits, appropriate remedial measures shall be applied to the foundation(s) and/or the structure that it is supporting so that appropriate reliability is maintained.
Tolerable settlements used throughout these provisions were established from theoretical considerations and empirical observations of bridge performance based on the work of Moulton (1984) and Duncan and Tan (1991). Three different serviceability conditions corresponding to different levels of required maintenance and repair were initially considered:
- 1) minor damage generally corresponding to the theoretical onset of deck cracking (Duncan and Tan, 1991),
- 2) more significant damage corresponding to the onset of structural distress based on empirical observations by Moulton (1986) and
- 3) major damage corresponding to theoretical overstress of the bridge superstructure (Moulton, 1986).
Target reliabilities for each of these conditions were established based on economic analyses described in Bowders et al. (2011). Comparative analyses for typical design conditions were then performed to evaluate the alternative serviceability conditions. Results of these analyses generally indicate that the first serviceability condition, corresponding to minor damage, tends to control foundation dimensions. These guidelines therefore only require evaluation of this condition (the others being presumed to be inherently satisfied based on the analyses performed).
Based on this work, tolerable settlements are established according to an angular distortion, defined as
| (dimensionless) | Equation Commentary 751.37.4.1 |
where :
- A = angular distortion (dimensionless),
- ∆ = differential settlement between adjacent bridge bents (consistent units of length),
- S = span between adjacent bridge bents (consistent units of length).
This limiting value of angular distortion is based on theoretical consideration of the onset of deck cracking (Duncan and Tan, 1991). This limit is explicitly included in the methods provided throughout EPG 751.37.
The target probabilities of exceedance reflected in the resistance factors provided in EPG 751.37 correspond to the target values established by MoDOT based on economic considerations. While use of alternative limits for tolerable settlement is possible, such use is not strictly appropriate since the target probabilities adopted by MoDOT for different classes of operational importance were established based on consequences associated with the limit provided in Equation Commentary 751.37.4.1. Other limits would generally require different target probabilities, and thus different resistance factors to achieve the same economic balance.
When results of evaluations performed for these provisions require that shaft dimensions be increased, designers should recognize that it has traditionally been more cost effective to increase the length of drilled shafts rather than increase the diameter of the shafts.
Commentary on EPG 751.37.4.1 Settlement of Individual Drilled Shafts using Approximate Method
The provisions of EPG 751.37.4.1 are based on an approximate load-settlement curve illustrated in Fig. Commentary 751.37.4.1.1. The load-settlement curve is established considering factored side and tip resistance values that account for variability and uncertainty associated with the nominal side and tip resistance and associated with mobilization of side and tip resistance. The following assumptions are also made:
- the shaft can be considered as practically rigid over the length of the shaft where significant side resistance is mobilized so that side resistance and end resistance are simultaneously mobilized;
- side and tip resistance are mobilized according to the bi-linear curves shown in Fig. Commentary 751.37.4.1.2;
- ultimate side resistance is fully mobilized at shaft displacements of 0.5 percent of the shaft diameter and
- ultimate tip resistance is fully mobilized for shaft displacements of 5 percent of the shaft diameter.
Based on these assumptions, the approximate factored load-settlement curve can be constructed by establishing the factored resistance and associated settlement values at the points designated as “a” and “b” in Fig. Commentary 751.37.4.1.1. The mobilized factored resistance at point a is computed as:
| RaR = RsR + 0.1 RpR | (consistent units of force) | Equation Commentary 751.37.4.2 |
where:
- RaR = factored total resistance at point a (consistent units of force),
- RsR = total factored side resistance determined according to the provisions of this article (consistent units of force) and
- RpR = factored tip resistance determined according to the provisions of this article (consistent units of force).
The corresponding settlement at point a is taken to be:
| (consistent units of length) | Equation Commentary 751.37.4.3 |
where:
- δa = settlement corresponding to point a (consistent units of length) and
- D = shaft diameter (consistent units of length).
The mobilized factored resistance at point b is computed as:
| RbR = RsR + RpR | (consistent units of force) | Equation Commentary 751.37.4.4 |
where:
- RbR = factored total resistance at point b (consistent units of force),
- RsR = total factored side resistance determined according to the provisions of this article (consistent units of force) and
- RpR = factored tip resistance determined according to the provisions of this article (consistent units of force).
The corresponding settlement at point b is taken to be
| (consistent units of length) | Equation Commentary 751.37.4.5 |
where:
- δb = settlement corresponding to point b (consistent units of length) and
- D = shaft diameter (consistent units of length).
The factored settlement due to a factored service load can then be determined by interpolation from the approximate load-settlement curve. Equations Commentary 751.37.4.3 and Commentary 751.37.4.4 produce such interpolated values with an additional term being added to account for elastic compression of the unsupported length of the shaft. For the purposes of this provision, the unsupported length shall be taken to be the length of shaft over which side resistance is neglected.
As has been done throughout these guidelines, factored loads are denoted using as a general reference to factored loads. This notation should not be taken to imply inclusion or exclusion of any specific load effects or load combinations, but rather is simply intended as a convenient notation to reflect factored loads. When applying these provisions of the guidelines, designers should replace with the appropriate load combinations and load factors for the relevant limit state. For this article, such load combinations and load factors should correspond to the appropriate serviceability limit state in which load factors are generally taken to be 1.0.
The modulus of elasticity used in Equation 751.37.4.7 should reflect the composite modulus for the shaft including the concrete and reinforcing steel.
The settlement resistance factor for elastic compression is placed in the denominator of Equation 751.37.4.7 as a matter of choice so that resistance factors are less than 1.0 as is conventionally assumed.
Settlement resistance factors for elastic compression provided in Table 751.37.4.1 were developed from probabilistic analyses performed considering the variability in the dead and live loads, the variability in concrete modulus, and the variability in the shaft area. The variability used for dead and live loads was taken from Kulicki et al. (2007). Variabilities in concrete modulus and shaft area were estimated from preliminary results of an ongoing study of the variability of these parameters (Tyler, 2010). Because these estimates are preliminary, it is likely that the settlement resistance factors for elastic compression can be refined with additional study of the variability of concrete modulus and shaft area.
The resistance factors provided in Figures 751.37.4.1.1 through 751.37.4.1.12 were established from preliminary probabilistic calibrations to achieve established target reliabilities as described in Vu and Loehr (2011). Considerable judgment was applied in development of these resistance factors in an effort to make these guidelines as comprehensive as possible. However, the resistance factors should be considered as rational but preliminary design values that can be dramatically improved through more comprehensive analysis of available full-scale load test results. The resistance factors provided were established with explicit consideration of the variability and uncertainty present for dead and live loads, for the nominal side and tip resistance, and for the anticipated mobilization of side and tip resistance. The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). Variability and uncertainty in the nominal side and tip resistances were established from statistical analysis of the empirical data as described in Loehr et al. (2011b). Variability and uncertainty in mobilization of side and tip resistance were estimated from preliminary analysis of results from a limited number of full-scale load tests. Additional study of the serviceability provisions of these guidelines should include more rigorous analysis of available load test data to establish improved models for load transfer in different types of materials, re-calibration of resistance factors for both the approximate method and t-z method provided in the guidelines, as well as consideration of alternative simplified and closed-form methods for prediction of settlements for drilled shafts (e.g. Vesic, 1977; Chen and Kulhawy, 2002; Mayne and Harris, 1993; O’Neill et al, 1996; etc.).
Probabilistic calibration of resistance factors for settlement of individual drilled shafts in cohesionless soils have not been completed at this time. Settlement evaluations should therefore be conducted according to current AASHTO LRFD Bridge Design Specifications. However, it is important to note that such designs will not generally produce the target probabilities established by MoDOT.
Commentary on EPG 751.37.4.2 Settlement of Individual Drilled Shafts using t-z Method
The settlement resistance factors used in the provisions of this article are akin to t-multipliers for t-z models and q-multipliers for q-w models, where the respective multipliers are selected to produce the target reliabilities for settlement established by MoDOT, as illustrated in Fig. Commentary 751.37.4.2. Application of resistance factors for use in commercial specialty software or spreadsheet programs therefore requires no special capabilities beyond that required for conventional analyses.
The program TZPile© is commercially available through Ensoft, Inc. Other similar programs are also commercially available from other vendors.
The modulus of elasticity used in the t-z analyses should reflect the composite modulus for the shaft including the concrete and reinforcing steel.
Elastic compression of shafts is inherently included in results of t-z analyses so no additional account shall be made for elastic compression of the shaft.
Results of preliminary analyses suggest that the variability and uncertainty associated with the shaft stiffness (EA) used in t-z analyses can be substantial (Tyler, 2010). For this version of the guidelines, the decision was made to combine the variability and uncertainty associated with shaft stiffness together with other sources of variability and uncertainty rather than to consider it separately. This decision simplifies use of the provisions, but does not allow for explicit accounting of the effects of the variability in shaft stiffness. Further study is needed to determine whether this position is a prudent one or whether separate resistance factors should be applied to shaft stiffness to allow the effect to be isolated.
The resistance factors provided in Figures 751.37.4.2.1 through 751.37.4.2.12 were established from preliminary probabilistic calibrations to achieve established target reliabilities as described in Vu and Loehr (2011). Considerable judgment was applied in development of these resistance factors in an effort to make these guidelines as comprehensive as possible. However, the resistance factors should be considered as rational but preliminary design values that can be dramatically improved through more comprehensive analysis of available full-scale load test results. The resistance factors provided were established with explicit consideration of the variability and uncertainty present for dead and live loads, for the nominal side and tip resistance, and for the anticipated mobilization of side and tip resistance. The variability and uncertainty utilized for dead load and live load were taken from Kulicki et al. (2007). Variability and uncertainty in the nominal side and tip resistances were established from statistical analysis of the empirical data as described in Loehr et al. (2011b). Variability and uncertainty in mobilization of side and tip resistance were estimated from preliminary analysis of results from a limited number of full-scale load tests. Additional study of the serviceability provisions of these guidelines should include more rigorous analysis of available load test data to establish improved models for load transfer in different types of materials, re-calibration of resistance factors for both the approximate method and t-z method provided in the guidelines, as well as consideration of alternative simplified and closed-form methods for prediction of settlements for drilled shafts (e.g. Vesic, 1977; Chen and Kulhawy, 2002; Mayne and Harris, 1993; O’Neill et al, 1996; etc.).
Model specific calibrations for individual t-z and q-w models have not been completed at this time. The resistance factors provided in these guidelines were established from preliminary calibrations for several simplified models. While the resistance factors produced from these calibrations, and provided in these guidelines, represent a rational design position, additional research is needed to refine these calibrations to reflect specific t-z and q-w models for different soil/rock types. Such calibrations are likely to increase the settlement resistance factors, which will improve the efficiency of drilled shafts designed according to these guidelines if serviceability controls the shaft dimensions.
Probabilistic calibration of resistance factors for settlement of individual drilled shafts in cohesionless soils have not been completed at this time. Settlement evaluations should therefore be conducted according to current AASHTO LRFD Bridge Design Specifications. However, it is important to note that such designs will not generally produce the target probabilities established by MoDOT.
Commentary on EPG 751.37.4.3 Settlement of Drilled Shafts in Groups
Commentary on Settlement of Shaft Groups in Cohesive Soils
This subarticle is currently unchanged from prior versions of the EPG aside from minor editorial revisions. Probabilistic calibrations for drilled shaft groups in cohesive soils have not been completed at this time.
Commentary on Settlement of Shaft Groups in Cohesionless Soils Using Standard Penetration Test Measurements
This subarticle is currently unchanged from prior versions of the EPG aside from minor editorial revisions. Probabilistic calibrations for drilled shaft groups in cohesionless soils have not been completed at this time.
Commentary on Settlement of Shaft Groups in Cohesionless Soils Using Cone Penetration Test Measurements
This subarticle is currently unchanged from prior versions of the EPG aside from minor editorial revisions. Probabilistic calibrations for drilled shaft groups in cohesionless soils have not been completed at this time.
Commentary on Settlement of Shaft Groups in Rock
This subarticle is new to the EPG, but relies exclusively on methods and resistance factors established for other provisions of the EPG.
Commentary on EPG 751.37.5 Design for Lateral Loading at Strength and Service Limit States
This subarticle is currently unchanged from prior versions of the EPG aside from minor editorial revisions. Probabilistic calibrations for laterally loaded shafts have not been completed at this time.
Commentary on EPG 751.37.6 Structural Resistance of Drilled Shafts
This subarticle is currently unchanged from prior versions of the EPG aside from minor editorial revisions.
The LRFD requirement that reinforcing steel extend 10 feet below the point of fixity shall not be taken to imply that rock sockets shall be a minimum of 10 feet long. This provision is intended to ensure that reinforcing steel extends beyond where significant bending may be encountered in the shaft, the location of which if not coincident with the point of fixity (pof) but higher than the pof may provide reasoning for using a lesser but adequate development length for a lesser bending moment at the pof and hence a shorter socket length., Regardless, reinforcement shall be provided for the full length of the shaft.
Commentary on EPG 751.37.7 References
AASHTO (2009), AASHTO LRFD Bridge Design Specification: Customary U.S. Units, American Association of State Highway and Transportation Officials, Fourth Edition with 2008 and 2009 Interim Revisions.
Abu El-Ela, A.A., J.J. Bowders, and J.E. Loehr (2011), Calibration of LRFD Resistance Factors for Design of Spread Footings in Hard and Soft Rock, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Bowders, J.J., J.E. Loehr, and D.R. Huaco (2011), MoDOT Transportation Geotechnics Research Program: Development of Target Reliabilities for MoDOT Bridge Foundations and Earth Slopes, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Chen, Y-J, and F.H. Kulhawy (2002), “Evaluation of Drained Axial Capacity for Drilled Shafts,” Deep Foundations 2002: An International Perspective on Theory, Design, Construction, and Performance, Geotechnical Special Publication No. 116, M.W. O’Neill and F.C. Townsend, Editors, ASCE, Reston, VA, pp. 1200-1214.
Duncan, J.M., and C.K. Tan (1991), “Part 5 – Engineering Manual for Estimating Tolerable Movements for Bridges,” in Manuals for the Design of Bridge Foundations, NCHRP Report 343, by R.M. Barker, J.M. Duncan, K.B. Rojiani, P.S.K. Ooi, C.K. Tan, and S.G. Kim, Transportation Research Board, pp. 219-228.
Hoek, E., and E.T. Brown (1988), “The Hoek-Brown Failure Criterion – A 1988 Update,” Proceedings of the 15th Canadian Rock Mechanics Symposium, Toronto, Canada.
Hoek, E. and E.T. Brown (1997), “Practical Estimates of Rock Mass Strength,” International Journal of Rock Mechanics and Mining Sciences, Vol. 34, No. 8, Elsevier, pp. 1165-1186.
Horvath, R.G., and T.C. Kenney (1979), “Shaft Resistance of Rock Socketed Drilled Piers,” Proceedings of the Symposium on Deep Foundations, ASCE, pp. 182-214.
Kulicki, J.M., Z. Prucz, C.M. Clancy, D.R. Mertz, and A.S. Nowak (2007), Updating the Calibration Report for AASHTO LRFD Code, Final Report for NCHRP Project 20-7/186, AASHTO, 125 pp.
Loehr, J.E., B.L. Rosenblad, and T.T. Vu (2011a), MoDOT Transportation Geotechnics Research Program: Drilled Shaft Axial Load Test Program Interpretation Report, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Loehr, J.E., S.A. Grant, and B.L. Rosenblad (2011b), Calibration of Resistance Factors for Design of Drilled Shafts at Strength Limit States Using Laboratory Test Measurements, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Mayne, P.W., and D.E. Harris (1993), Axial Load-Displacement Behavior of Drilled Shaft Foundations in Piedmont Residuum, FHWA Reference Number 41-30-2175, Georgia Tech Research Corporation, Atlanta, GA.
Miller, A.D. (2003), Prediction of Ultimate Side Shear for Drilled Shafts in Missouri Shales, thesis presented to the faculty of the University of Missouri in partial fulfillment of the requirements for M.S. degree, 266 pp.
Moulton, L.K. (1986), Tolerable Movement Criteria for Highway Bridges, Report No. FHWA-TS-85-228, Federal Highway Administration, McLean, VA, 93 pp.
O'Neill, M.W., F.C. Townsend, K.H. Hassan, A. Buller, and P.S. Chan (1996), Load Transfer for Drilled Shafts in Intermediate Geomaterials, Publication No. FHWA-RD-95-171, Federal Highway Administration, McLean, VA, 184 pp.
O’Neill, M.W., and L.C. Reese (1999), Drilled Shafts: Construction Procedures and Design Methods, Report No. FHWA-IF-99-025, Federal Highway Administration, McLean, VA, 758 pp.
Phoon, K.K., and F.H. Kulhawy (2005), “Characterization of Model Uncertainties for Drilled Shafts Under Undrained Axial Loading,” Contemporary Issues in Foundation Engineering, Proceedings of Sessions from the Geo-Frontiers 2005 Congress, Austin, Texas, ASCE Geo-Institute, GSP 131.
Pierce, M.D., J.E. Loehr, and B.L. Rosenblad (2011), Calibration of LRFD Resistance Factors for Design of Drilled Shafts at Strength Limit States Using In situ Test Measurements, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Rosenblad, B.L., J.E. Loehr, M.D. Pierce, S.A. Grant, and K.D. Murphy (2011), MoDOT Transportation Geotechnics Research Program: Drilled Shaft Axial Load Test Program Data Report, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Turner, J.P. (2006), Rock-socketed Shafts for Highway Structure Foundations, NCHRP Synthesis 360, Transportation Research Board, 136 pp.
Tyler, H.L. (2010), Influence of Parameter Variability on Side Shear Values Determined from O-Cell Testing of Drilled Shafts, report presented to the University of Missouri in partial fulfillment of the requirements for M.S. Degree.
Vu, T.T., and J.E. Loehr (2011), Calibration of LRFD Resistance Factors for Design of Drilled Shafts at Serviceability Limit States, Missouri Department of Transportation, OR11.XXX, XXX pp. (in preparation)
Vesic, A.S. (1977), NCHRP Synthesis 42: Design of Pile Foundations, Transportation Research Board, National Research Council, Washington, D.C., 68 pp.
Wyllie, D.C. (1999), Foundations on Rock, E & FN Spon, Second Edition, 401 pp.

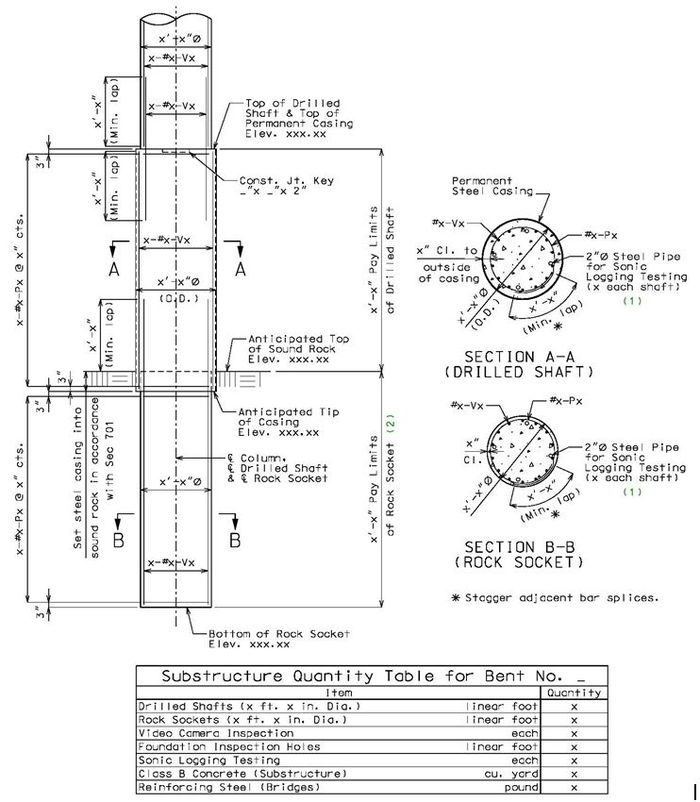



















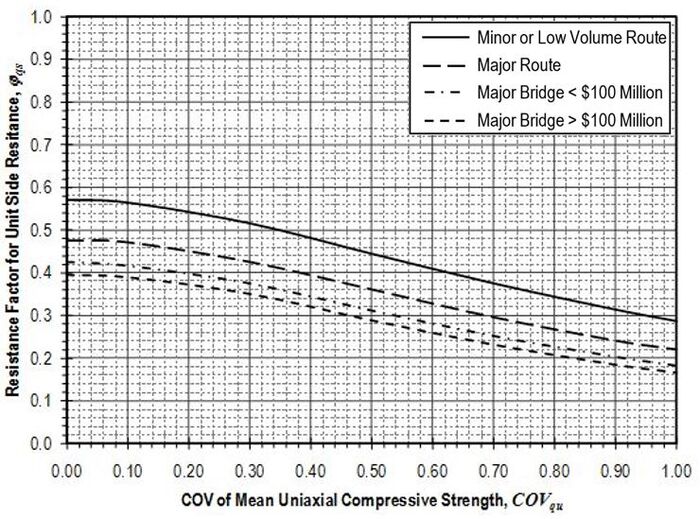
![{\displaystyle q_{p}={\sqrt {s}}\cdot {\overline {q_{u}}}{\Bigg [}1+{\sqrt {{\frac {m}{\sqrt {s}}}+1}}{\Bigg ]}\leq 400ksf}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b692a3d03dae2cade55e85bf95aceb7ddb7c87)

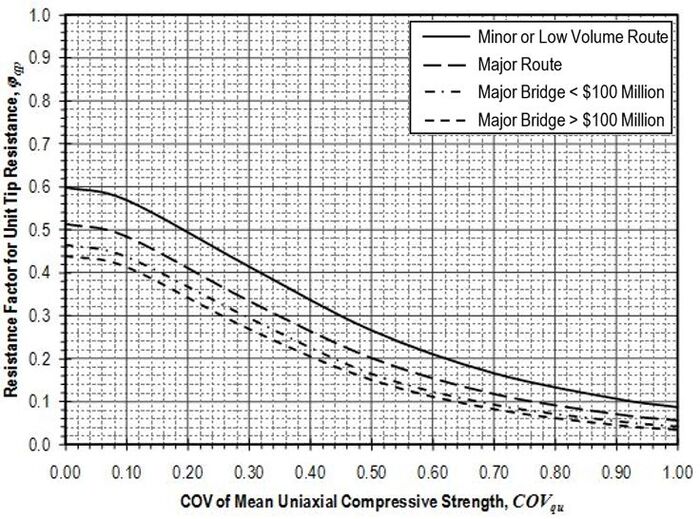













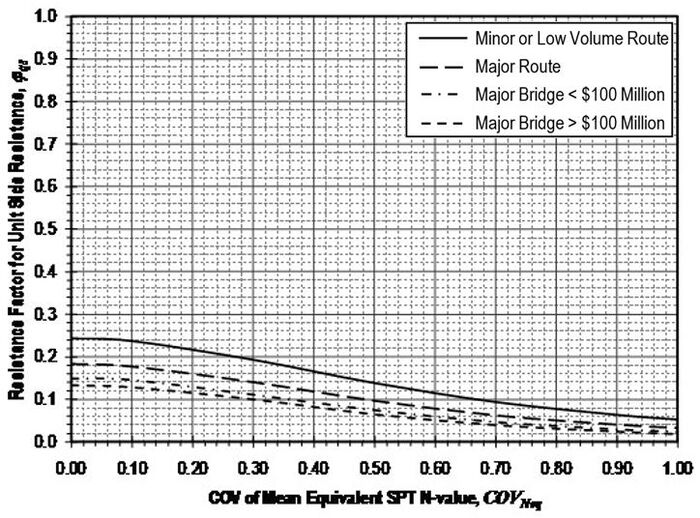

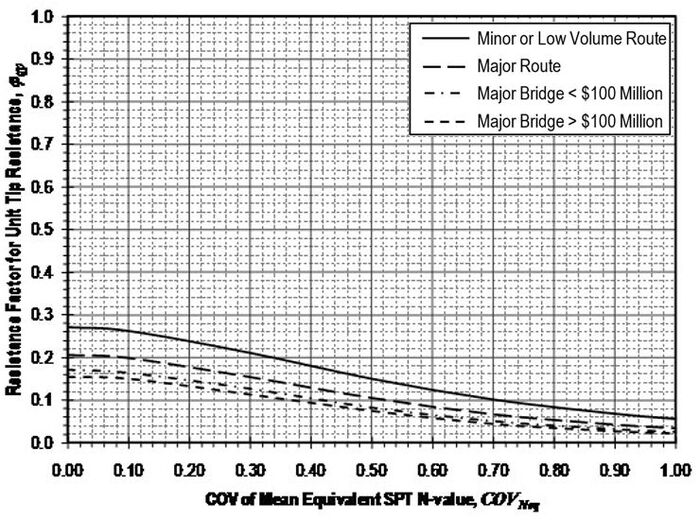




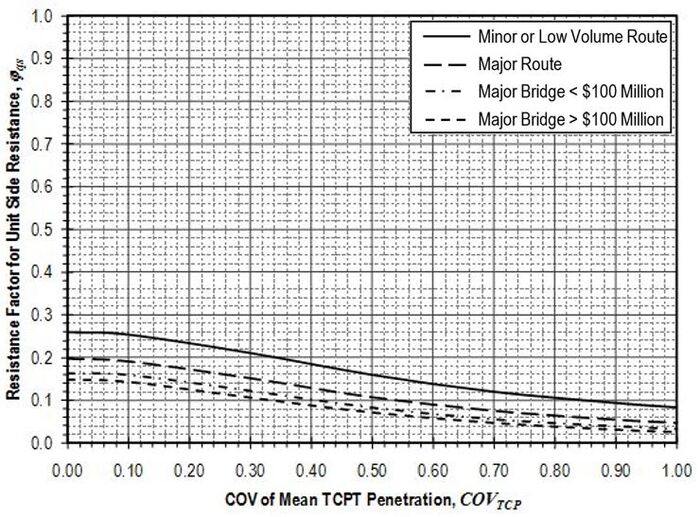

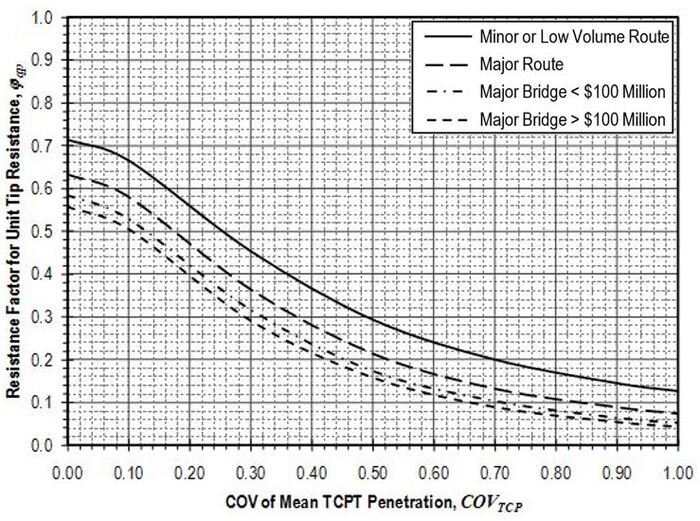




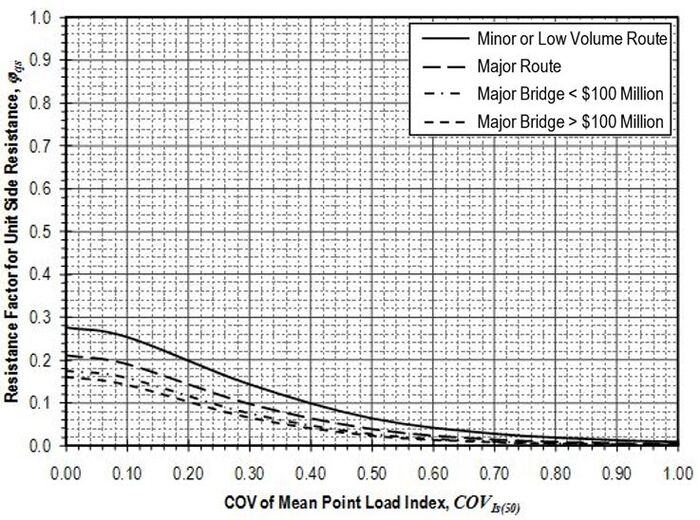







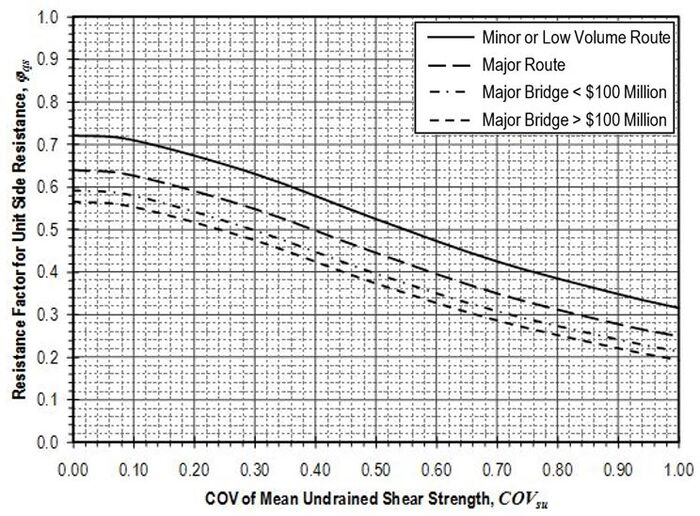

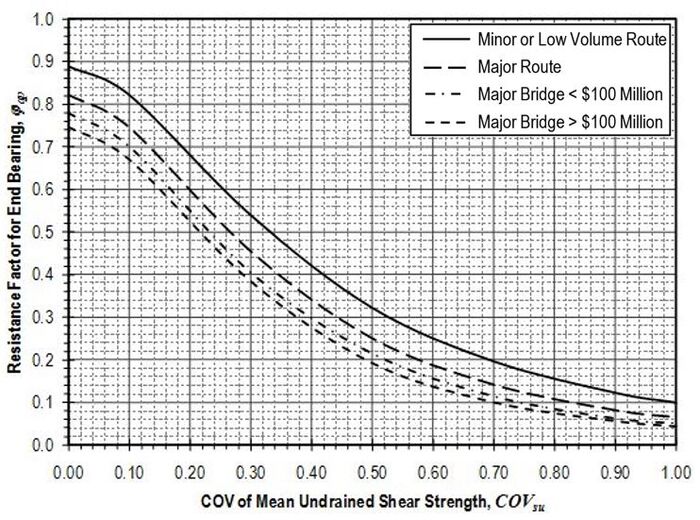
![{\displaystyle N_{c}=6{\Big [}1+0.2{\Big (}{\frac {Z}{D}}{\Big )}{\Big ]}\leq 9}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1f18fe8f0a68395d18987fc393006242cdf6621)























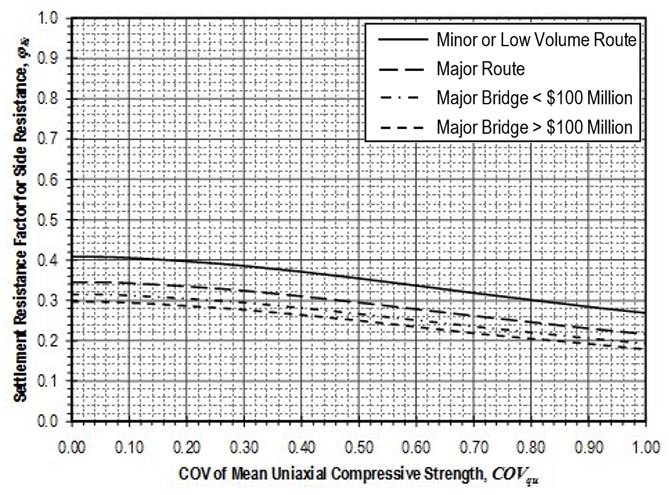
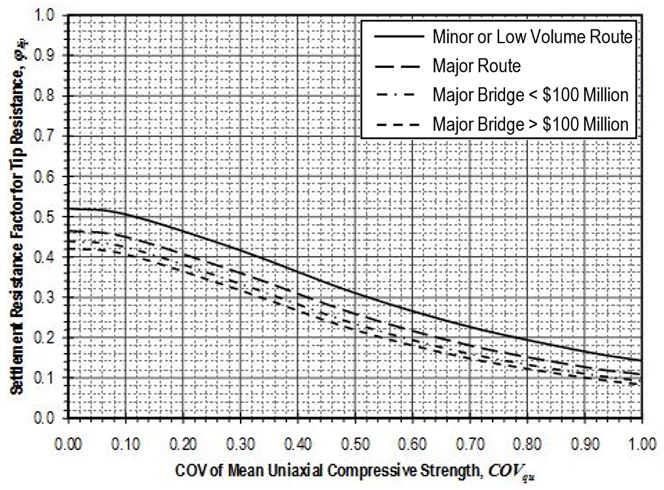
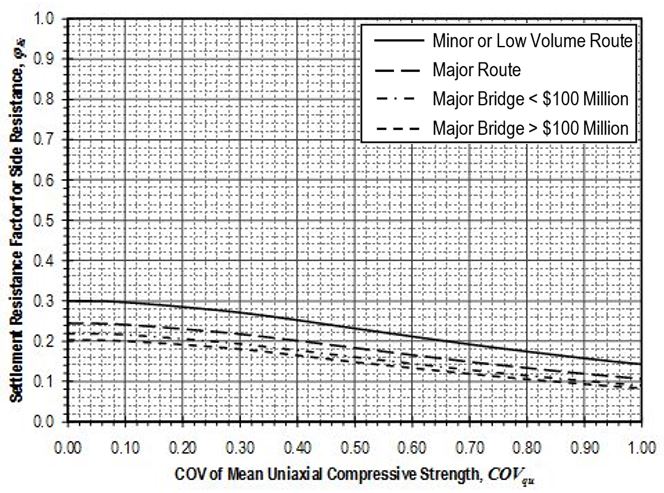


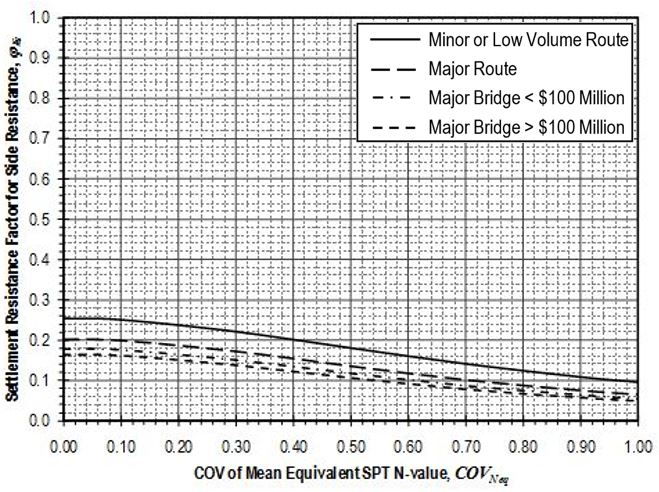
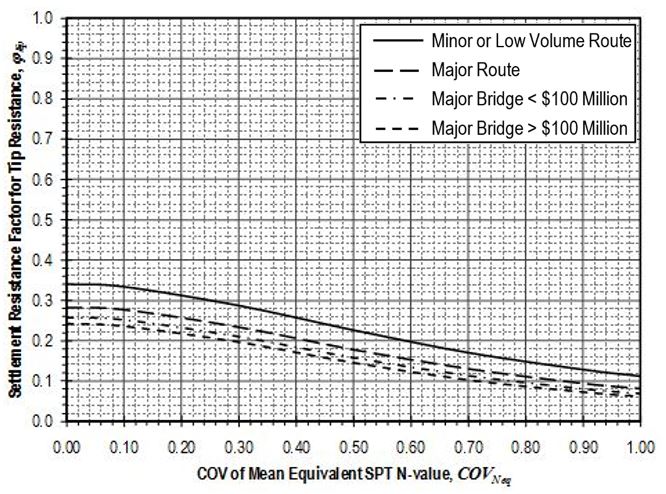

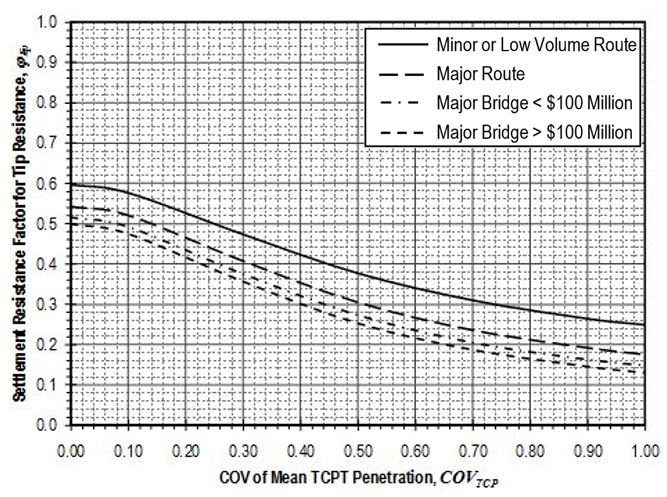
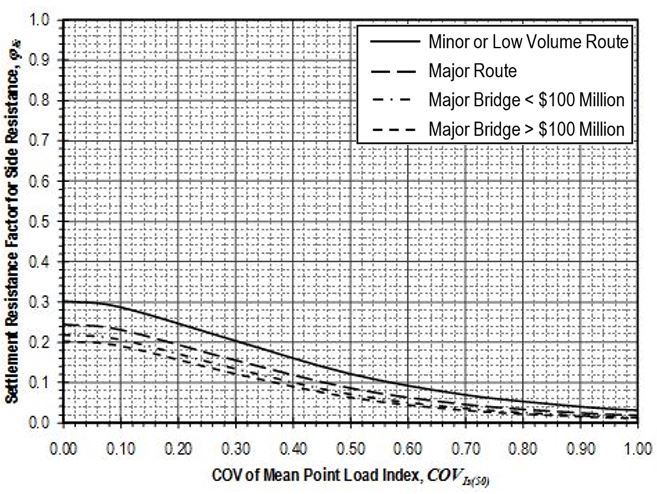

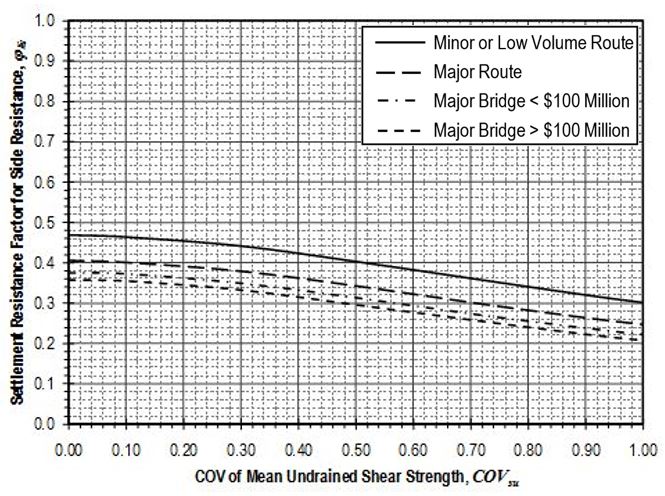





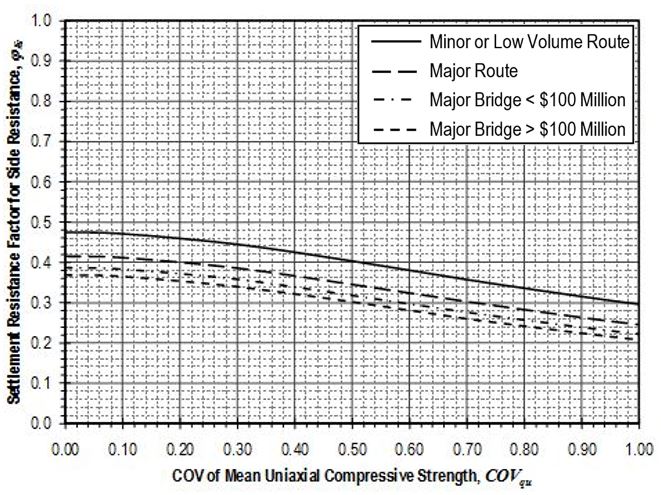
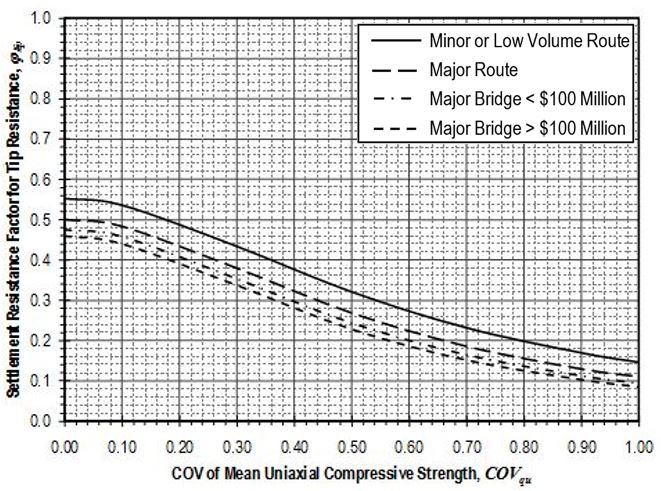

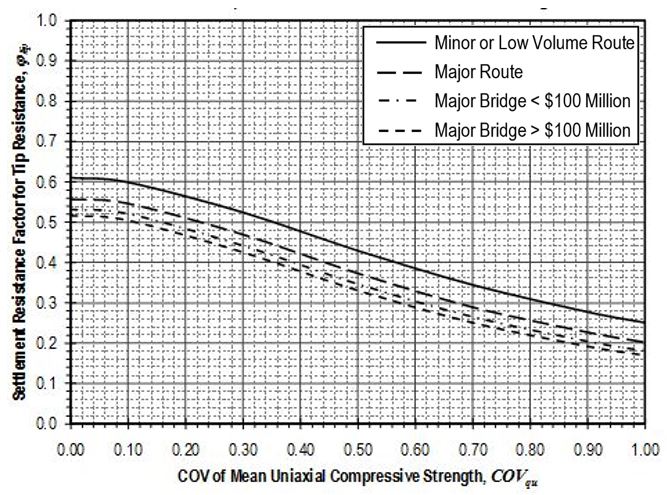

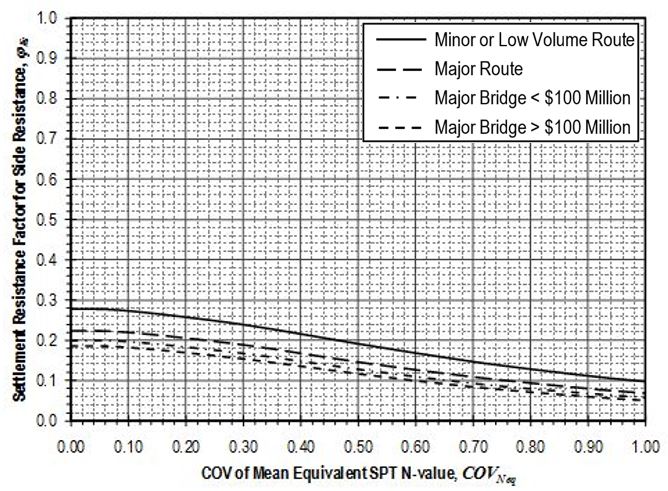
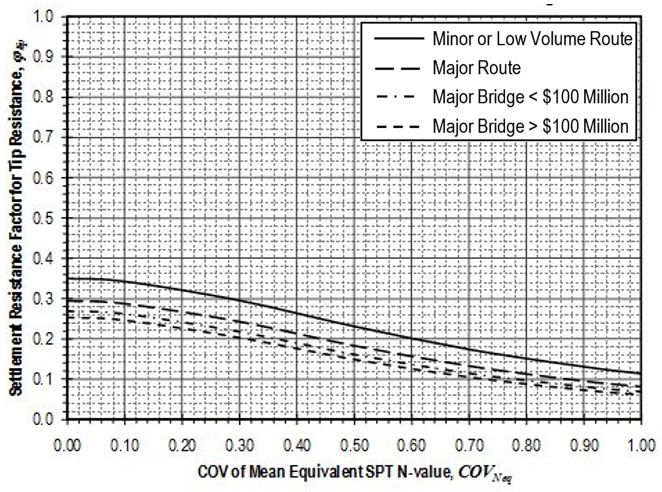
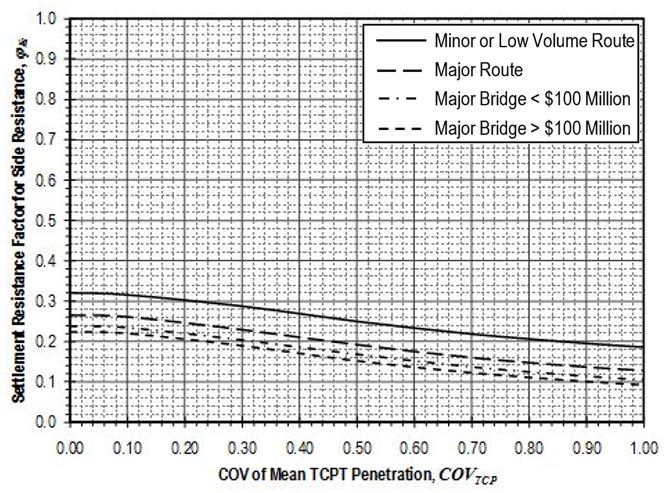
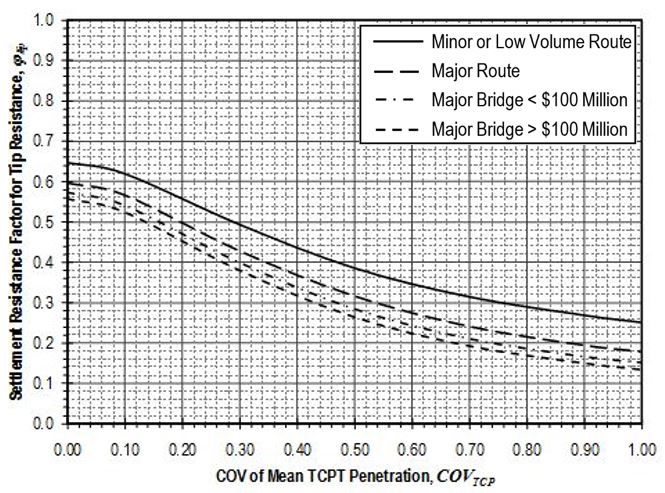
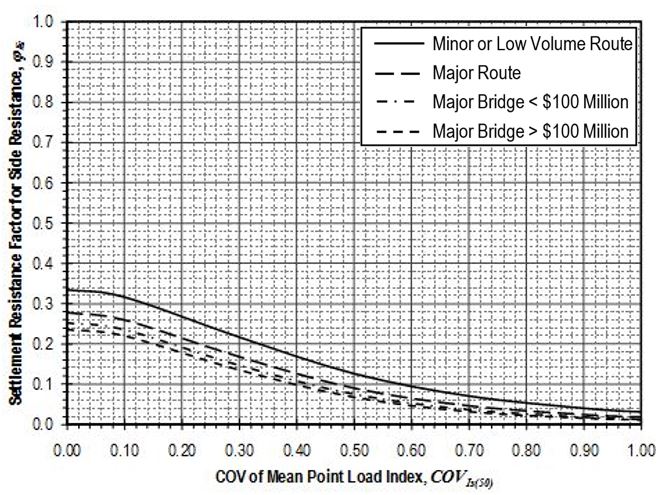
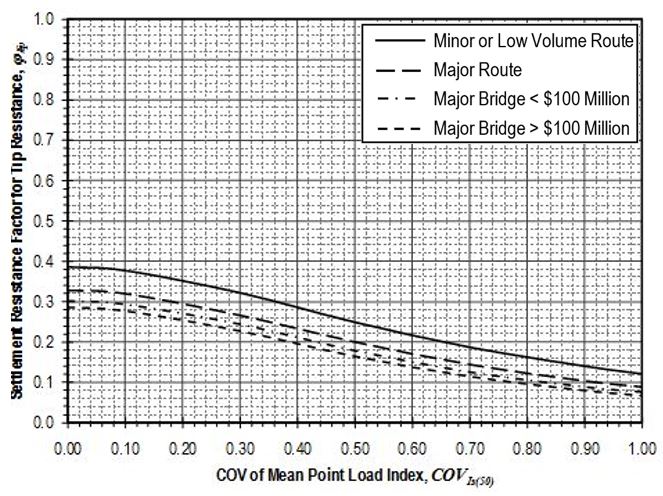

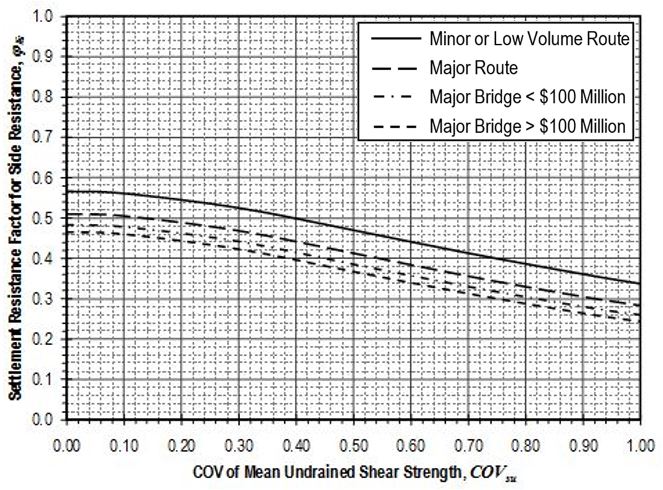
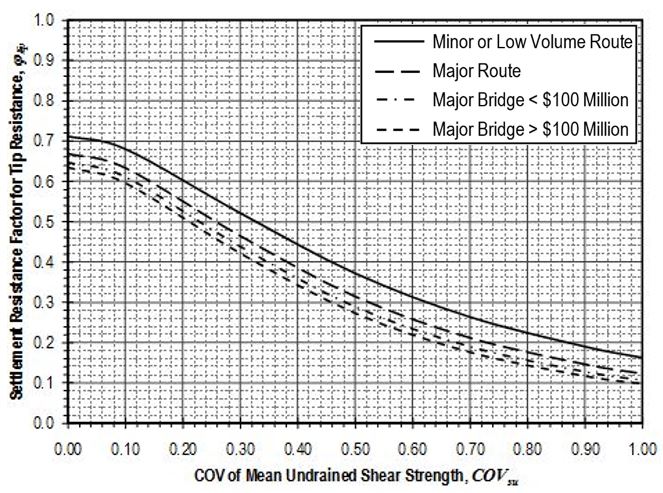


![{\displaystyle {\Big [}0.77log_{10}{\Big (}{\frac {40}{\sigma _{v}^{'}}}{\Big )}{\Big ]}\leq 2.0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3990c94819a620e3fc42d8292f130202231c34ed)





![{\displaystyle P_{N}=0.85{\Big [}0.85f_{c}^{'}{\big (}A_{g}-A_{steel}{\big )}+A_{steel}f_{y}{\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cd953fda2ae315493d67fb8e9007066c74c19cb)
![{\displaystyle P_{N}=0.80{\Big [}0.85f_{c}^{'}{\big (}A_{g}-A_{steel}{\big )}+A_{steel}f_{y}{\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c297a813416e6d719238ec0f3c9986fa95bb023)