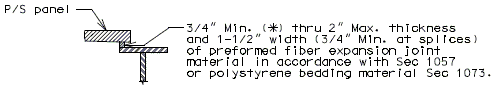751.40 LFD Widening and Repair
751.40.8.12 Concrete Pile Cap Intermediate Bents
751.40.8.13 Concrete Pile Cap Non-Integral End Bents
751.40.8.14 Concrete Pile Cap Integral End Bents
751.40.8.15 Cast-In-Place Concrete Retaining Walls
- 751.40.8.15.1 Loads
- 751.40.8.15.3 Unit Stresses
- 751.40.8.15.4 Design
- 751.40.8.15.5 Example 1: Spread Footing Cantilever Wall
- 751.40.8.15.6 Example 2: L-Shaped Cantilever Wall
- 751.40.8.15.7 Example 3: Pile Footing Cantilever Wall
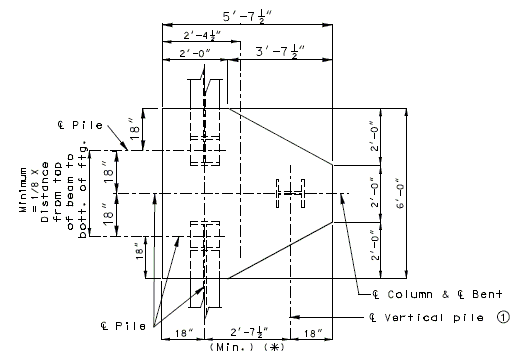
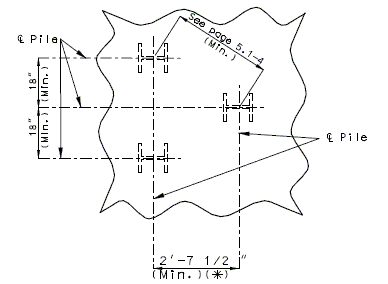
- 751.40.8.15.8 Dimensions
- 751.40.8.15.9 Reinforcement
- 751.40.8.15.10 Details
751.40.1 General
751.40.1.1 Widening and Repair of Existing Structures
The Federal Highway Administration and the States have established a goal that the LRFD standards be used on all new bridge designs after October 2007. For modification to existing structures and with the approval of the Structural Project Manager or Structural Liaison Engineer, the LRFD Specifications or the specifications which were used for the original design, may be used by the designer.
751.40.2 Deck Treatments
751.40.2.1 Resurfacing
 |
| PLAN |
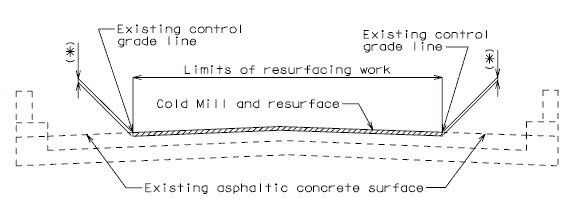 |
| SECTION THRU ROADWAY |
Place the following notes on plans.
- The existing asphaltic concrete surface shall be removed to a uniform grade line * below the existing control grade line as noted.
- Resurface with * Asphaltic Concrete.
- * Depth of asphaltic concrete as specified in the Bridge Memorandum.
751.40.2.2 Special Repair Zones
The following order of repair zones shall be used for the deck repair on continuous concrete structures.
Hydro Demolition Projects (Case 1 and 2)
Conventional deck repair required in the areas designated as special repair zones shall be completed before demolition in alphabetical sequence beginning with Zone A. Zones with the same letter designation may be repaired at the same time.
Any deck repair in areas not designated as a special repair zone shall be completed after hydro demolition. Case 1 is primarily monolithic deck repair after hydro demolition. Case 2 is primarily conventional deck repair after hydro demolition.
Note:
- - Case 1 shall not be used for polyester polymer and low slump concrete wearing surfaces (too stiff for monolithic repairs).
- - Conventional deck repair is required with void tube replacement after hydro demolition with both Case 1 and Case 2.
- - If an excessive number of zones are required at any bent, see the Structural Project Manager or Structural Liaison Engineer.
- - Consider combining zones if the length of a zone in the longitudinal direction of the bridge is less than 24 inches.
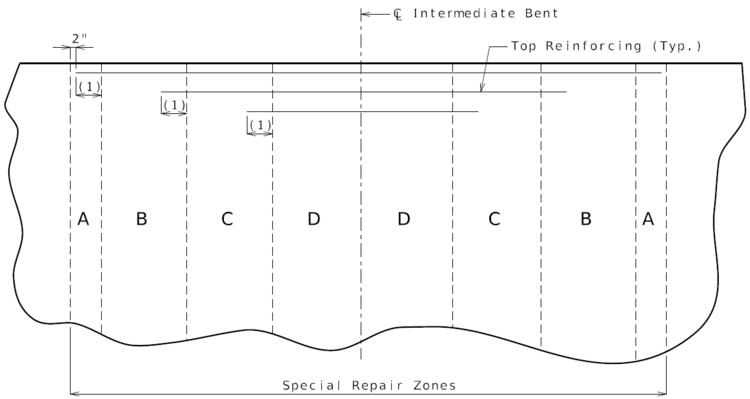 |
| PART PLAN OF SLAB SHOWING REPAIR ZONES (A, B, C and D) |
- (1) Development Length.
- See EPG 751.50 Standard Detailing Notes for appropriate notes.
Non-Hydro Demolition Projects
Any deck repair in areas not designated as a special repair zone shall be completed prior to work in Zone A. Zones with the same letter designation may be repaired at the same time.
Note:
- - If an excessive number of zones are required at any bent, see the Structural Project Manager or Structural Liaison Engineer.
- - Consider combining zones if the length of a zone in the longitudinal direction of the bridge is less than 24 inches.
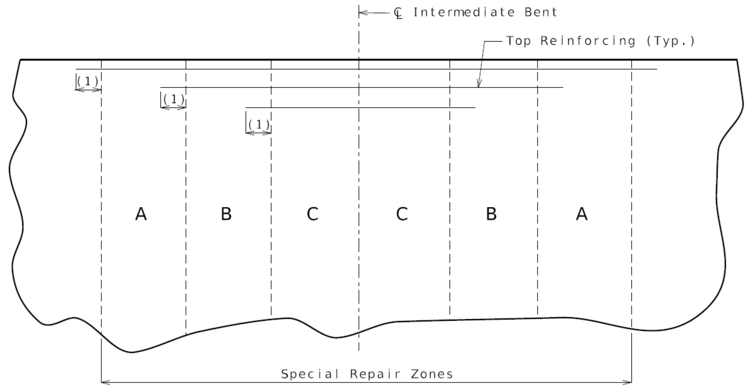 |
| PART PLAN OF SLAB SHOWING REPAIR ZONES (A, B and C) |
- (1) Development Length.
- See EPG 751.50 Standard Detailing Notes for appropriate notes.
751.40.2.3 Deck Repair and Filled Joints
Bridge Deck, Repair
Report 2002
See also: Research Publications
| Bridge Standard Drawings |
| Rehabilitation, Surfacing & Widening – RHB; Deck Rehab (Deck Repair and Wearing Surface Details) |
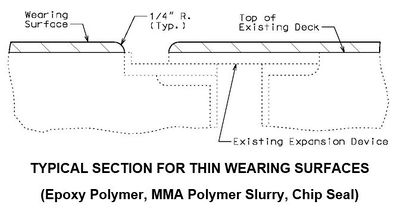
751.40.2.4 Wearing Surfaces
Replacement of Typical Expansion Joint Systems (Strip Seal Shown, Other Systems Similar)
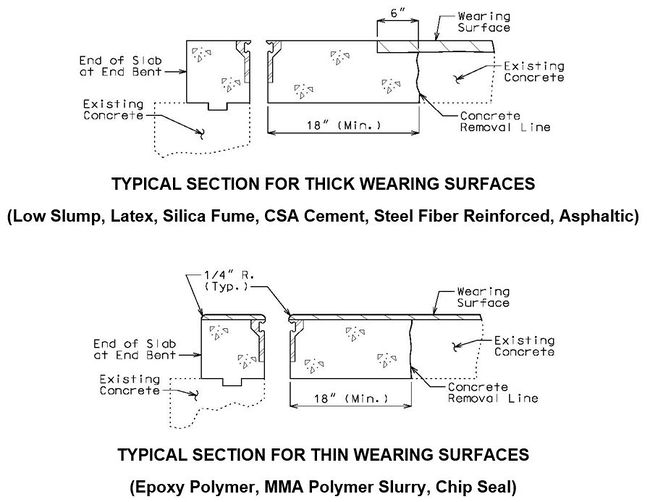
When concrete is removed and armor is replaced, see EPG 751.13 Expansion Joint Systems for the appropriate expansion joint system details and EPG 751.50 H5 for the appropriate notes.
For chip seals and polymer wearing surfaces, see EPG 751.50 I1 for the appropriate notes.
Elastomeric Expansion Joint System
When a thick wearing surface (low slump, latex, silica fume, CSA cement, steel fiber reinforced, asphaltic) is used, the elastomeric joint must be replace by another type of expansion joint system.

Flat Plate Expansion Joint System
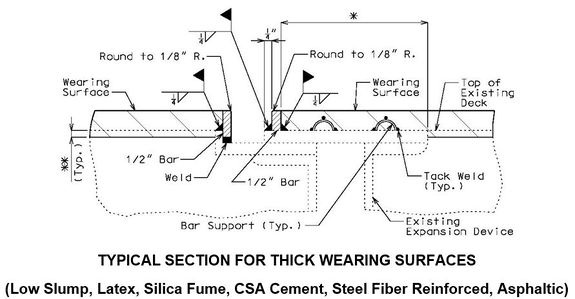
- * When this dimension exceeds 3" and a concrete wearing surface is used, tack weld a one inch bar chair to the plate for each 3" of plate to be covered by the wearing surface.
- ** Scarify existing slab. See the Bridge Memorandum for the minimum depth of scarification. Scarification not required for asphaltic concrete wearing surface.
- Note: See standard plans for Steel Dams at Expansion Joints.
751.40.2.5 Edge Treatments
751.40.2.5.1 Epoxy Coating
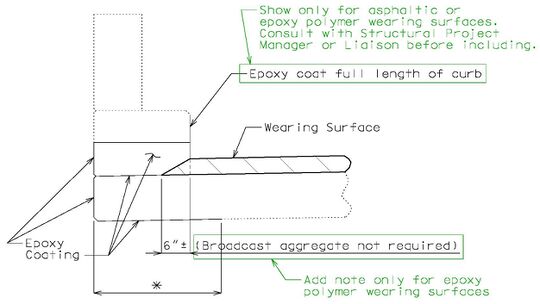 |
| TYPICAL SECTION OF EXISTING CURB OUTLET SHOWING LIMITS OF EPOXY COATING |
- Note:
- * Dimension to edge of girder or stringer ±. For bridges that do not have girders or stringers use 2'-6", except that if with thrie beam rail, then use 4'-0".
- Consult with Structural Project Manager or Liaison for making work incidental to another item or use of pay item "Cleaning and Epoxy Coating".
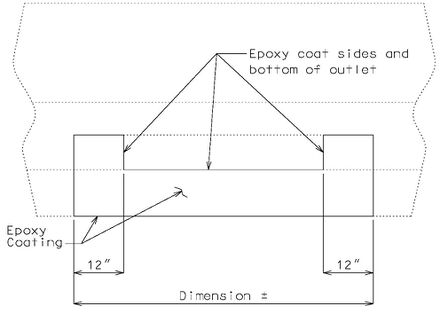
|
| TYPICAL ELEVATION OF EXISTING CURB OUTLET SHOWING LIMITS OF EPOXY COATING (Wearing surface not shown for clarity) |
751.40.2.5.2 Edge Repair
If slab edge repair is specified on the Bridge Memorandum when the barrier or railing is not removed or when full depth repair is not a pay item, the following detail shall be provided.
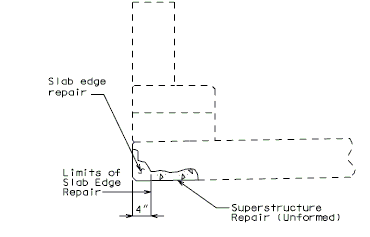 |
| CONCRETE EDGE REPAIR |
- If the barrier or railing is removed when full depth repair and slab edge repair are pay items, the following detail shall be provided.
 |
| CONCRETE EDGE REPAIR |
- * If the dimension exceeds 4 inches, the repair extending to the edge of slab will be paid for as Full Depth Repair.
751.40.2.6 Longitudinal Joints
REPLACEMENT OF EXISTING EXPANSION DEVICE
MEDIAN BARRIER
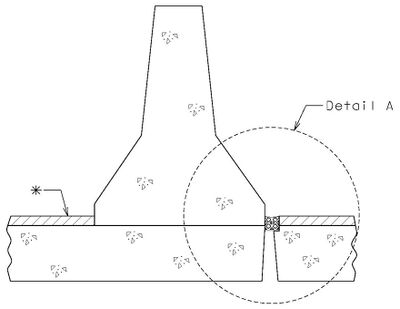 |
| SECTION THRU BARRIER |
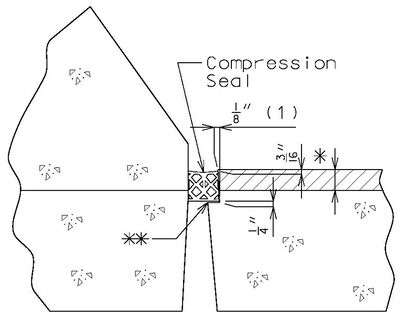 |
| DETAIL A |
- (1) May be cast vertical and saw cut to slant.
- * Latex Concrete Wearing Surface = 1-3/4".
Low Slump Concrete Wearing Surface = 2-1/4". - ** Cut minimum 1/2" support notch (rough finish). Remove any existing compression seal.
751.40.2.7 Temporary Traffic Control Device
Show Barrier as per district recommendation. Typically Barrier is shown when structure is on interstate and/or the rail is being removed. Otherwise, show the dimension lines with 2'-0" dimension.
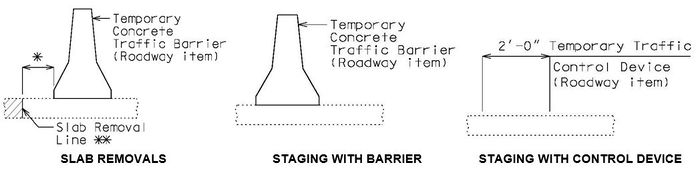
- * If this dimension is less than 3 feet, the temporary concrete traffic barrier shall be attached with tie-down straps, with the approval of the Structural Project Manager or Structural Liaison Engineer. Where lateral deflection cannot be tolerated, the temporary concrete traffic barrier shall be attached with the bolt through deck detail (to be used only on existing decks). See EPG 617.1 Temporary Traffic Barriers and EPG 751.1.2.12 Temporary Barriers.
- ** Where slab removal represents small and discontinuous openings in the deck along the bridge length (e.g. expansion device replacement) use of either a flat steel plate, a 22 ½” temporary traffic control device or a temporary concrete traffic barrier may be more appropriate. Consult with the Structural Project Manager or Structural Liaison Engineer.
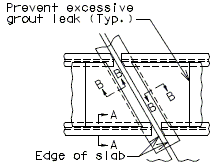
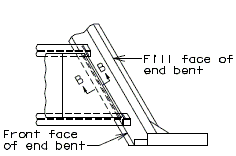
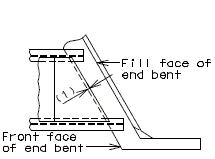
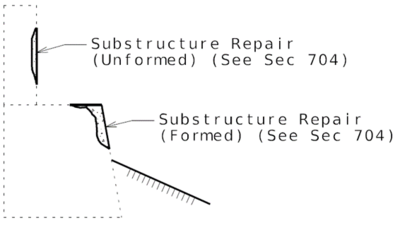
751.40.3 Substructure Repair
751.40.3.1 Formed and Unformed Repair Areas
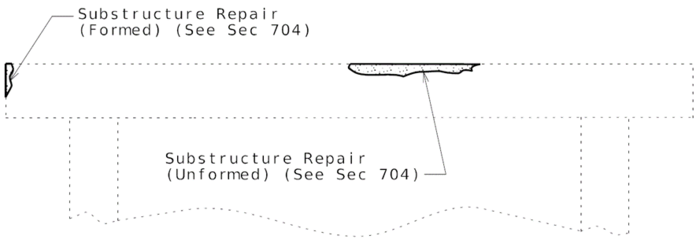 |
| Elevation of Int. Bent |
 |
| Section through End Bent |
751.40.3.2 Bent Cap Shear Strengthening using FRP Wrap
| Bridge Standard Drawings |
| Rehabilitation, Surfacing & Widening; Fiber Reinf. Polymer (FRP) Wrap for Bent Cap Strengthening [RHB08] |
Fiber Reinforced Polymer (FRP) wrap may be used for Bent Cap Shear Strengthening. FRP wrap may also be used for seismic retrofit of existing columns, but that procedure is not discussed herein (see EPG 751.9.1 Seismic Analysis and Design Specifications).
When to strengthen: When increased shear loading on an existing bent cap is required and a structural analysis shows insufficient bent cap shear resistance, bent cap shear strengthening is an option. An example of when strengthening a bent cap may be required: removing existing girder hinges and making girders continuous will draw significantly more force to the adjacent bent. An example of when strengthening a bent cap is not required: redecking a bridge where analysis shows that the existing bent cap cannot meet capacity for an HS20 truck loading, and the new deck is similar to the old deck and the existing beam is in good shape.
How to strengthen: Using FRP systems for shear strengthening follows from the guidelines set forth in NCHRP Report 678, Design of FRP System for Strengthening Concrete Girders in Shear. The method of strengthening, using either discrete strips or continuous sheets, is made optional for the contractor in accordance with NCHRP Report 678. A Bridge Standard Drawing and Bridge Special Provision have been prepared for including this work on jobs. They can be revised to specify a preferred method of strengthening if desired, strips or continuous sheet.
What condition of existing bent cap required for strengthening: If a cap is in poor shape where replacement should be considered, FRP should not be used. Otherwise, the cap beam can be repaired before applying FRP. Perform a minimum load check using (1.1DL + 0.75(LL+I))* on the existing cap beam to prevent catastrophic failure of the beam if the FRP fails (ACI 440.2R, Guide for the Design and Construction of Externally Bonded FRP, Sections 9.2 and 9.3.3). If the factored shear resistance of the cap beam is insufficient for meeting the factored minimum load check, then FRP strengthening should not be used.
- * ACI 440.2R: Guide for the Design and Construction of Externally Bonded FRP
Design force (net shear strength loading): Strengthening a bent cap requires determining the net factored shear loading that the cap beam must carry in excess of its unstrengthened factored shear capacity, or resistance. The FRP system is then designed by the manufacturer to meet this net factored shear load, or design force. The design force for a bent cap strengthening is calculated considering AASHTO LFD where the factored load is the standard Load Factor Group I load case. To determine design force that the FRP must carry alone, the factored strength of the bent cap, which is 0.85 x nominal strength according to LFD design, is subtracted out to give the net factored shear load that the FRP must resist by itself. NCHRP Report 678 is referenced in the special provisions as guidelines for the contractor and the manufacturer to follow. The report and its examples use AASHTO LRFD. Regardless, the load factor case is given and it is left to the manufacturer to provide for a satisfactory factor of safety based on their FRP system.
Other References:
- * ACI 201.1R: Guide for Making a Condition Survey of Concrete in Service
- * ACI 224.1R: Causes, Evaluation, and Repair of Cracks in Concrete
- * ACI 364.1R-94: Guide for Evaluation of Concrete Structures Prior to Rehabilitation
- * ACI 440.2R-08: Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures
- * ACI 503R: Use of Epoxy Compounds with Concrete
- * ACI 546R: Concrete Repair Guide
- * International Concrete Repair Institute (ICI) ICI 03730: Guide for Surface Preparation for the Repair of Deteriorated Concrete Resulting from Reinforcing Steel Corrosion
- * International Concrete Repair Institute (ICI) ICI 03733: Guide for Selecting and Specifying Materials for Repairs of Concrete Surfaces
- * NCHRP Report 609: Recommended Construction Specifications Process Control Manual for Repair and Retrofit of Concrete Structures Using Bonded FRP Composites
- * AASHTO Guide Spec for Design of Bonded FRP Systems for Repair and Strengthening of Concrete Bridge Elements, March 2023, 2nd Ed.
751.40.3.3 Steel HP Pile Maintenance and Repair
Maintenance/Repair Guidelines
Piles are primary structural members and are compressively loaded all the time which makes it important to safely inspect, maintain and repair them if necessary. Pile inspection will require an assessment of pile performance by looking for pile deterioration and measuring pile section loss in order to determine the level of pile maintenance/repair required. The following schedule may be used for selecting the level of maintenance/repair required:
| Pile Percent Section Loss | Method* | Level |
|---|---|---|
| 0% through 25% | Clean and recoat existing piles | Maintenance |
| >25% through 40% | Encasement of deteriorated section | Maintenance |
| >40% through 75% or holes in any element or local buckling of any element | Plating ** of deteriorated section OR replacement *** of section (splicing), AND encasement of the repaired section | Repair |
| >75% | Contact the Bridge Division | Repair |
| * Method may also include cleaning and recoating all exposed piles, and cleaning and recoating all remaining exposed pile sections after encasement and/or repair. | ||
| ** Plating can be for both flanges only, web only or both flanges and web. Overall symmetry of the pile cross-section shall be maintained when plating. | ||
| *** Based on additional factors other than just the percent of pile section loss, a replacement pile section (splicing) may be considered. Minimizing or eliminating traffic loading, adding falsework or just having support conditions such as integral bents (where both the pile cap beam and the superstructure concrete diaphragm are connected by more than just dowel bars – see bridge plans) can help to determine the method of repair. A replacement pile section can be coated or galvanized. See Structural Project Manager. | ||
Estimating Pile Percent Section Loss in the Field
Quantifying pile section loss can be inexact. To encourage uniform application of the maintenance/repair guidelines, the following procedure is recommended:
- 1. Pile section loss should be determined using a thickness meter.
- 2. Remove deteriorated material and clean pile for measurement.
- 3. At any point along a pile (cross-section) where there are three elements to be considered independently, e.g. two flanges and a web.
- 4. Estimate the actual cross-section area of each element at its most deteriorated point along the length of pile. Using the thickness meter, measure the thickness at several points along a horizontal line across the element. From this data, estimate the actual cross-section area of each element.
- 5. The fraction of section remaining (PSR) is the actual cross-section area of each element at its most deteriorated point along the length of pile divided by the original area of same element.
- 6. Percent section loss is 100(1 – PSR) for each element.
- 7. The greatest PSR dictates the maintenance/repair method.
- 8. Examine continuity at flange/web intersections. Section loss along these intersections along the length of pile of more than 6 linear inches should be repaired using encasement as either the only method or part of plating/replacing repair method regardless of a low percent section loss.
- 9. Interference from cross bracing at pile sections to be repaired will need special consideration not detailed on the standard drawings.
| Bridge Standard Drawings |
| Rehabilitation, Surfacing & Widening – RHB; Steel HP Pile Maintenance and Repair |
Additional types of maintenance and repairs may be considered which include but are not limited to:
- Zinc tape coating
- FRP strengthening
- Corrosion inhibitor
751.40.4 Barriers and Railings
751.40.4.1 End Post Modification for 12-inch Vertical Barrier (Safe & Sound Bridges)
The 12-inch vertical barrier requires modification to allow attachment of the transition for the Midwest Guardrail System.
| Bridge Standard Drawings |
| Barrier End Modifications – BEM & CBO/Barrier End Modification – BEM |
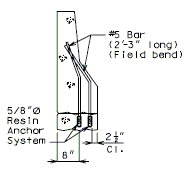
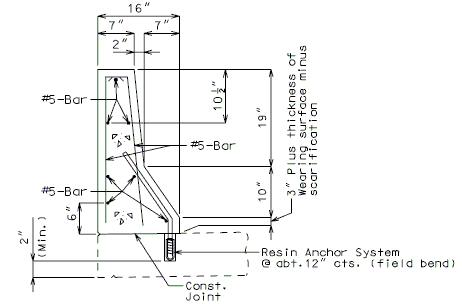
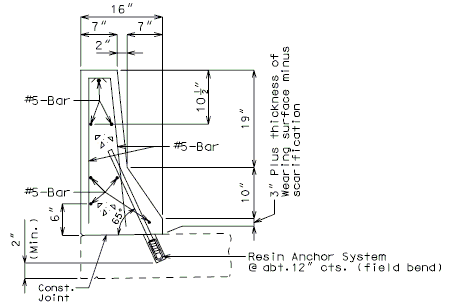
751.40.4.2 Replacement of Existing Type B Barrier Using Anchor Systems
NEW BARRIER ON SLAB
|
| SECTION THRU BARRIER |
|
| SECTION THRU BARRIER (OPTIONAL ANCHORING SYSTEM) |
| See EPG 751.50 I2. Resin & Cone Anchors for appropriate notes. |
NEW BARRIER ON WING
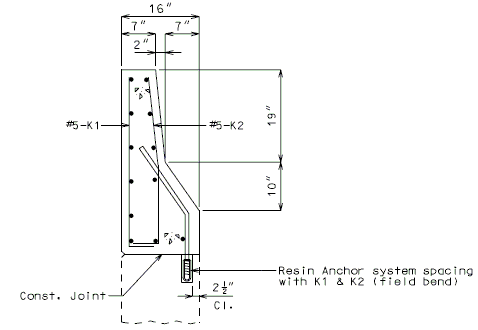
|
| SECTION THRU BARRIER(*) |
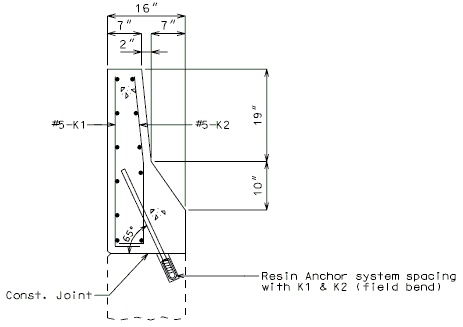
|
| SECTION THRU BARRIER(*) (OPTIONAL ANCHORING SYSTEM) |
- Note: See EPG 751.50 I2. Resin & Cone Anchors for appropriate notes. For details not shown, see EPG 751.12 Barriers, Railings, Curbs and Fences.
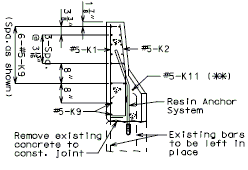
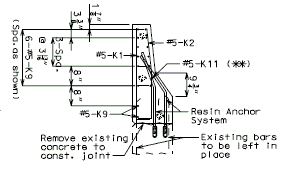
REPLACEMENT OF EXISTING BARRIER AT END OF WING USING ANCHOR SYSTEMS
INTEGRAL END BENTS
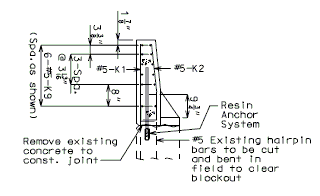 |
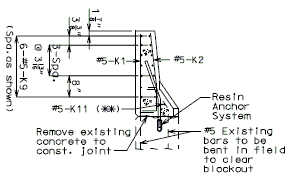 |
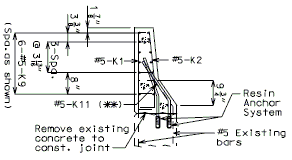
|
| SECTION A-A | SECTION B-B | SECTION C-C |
REPLACEMENT OF EXISTING BARRIER AT END OF WING USING ANCHOR SYSTEMS
NON-INTEGRAL END BENTS
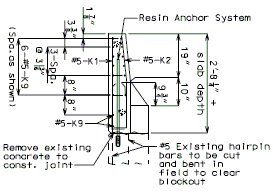 |
 | | 
| |
| SECTION A-A | SECTION B-B | SECTION C-C |
751.40.4.3 Replacement of Existing Rail with Thrie Beam Rail
As a matter of policy, blockouts for thrie beam railings are required while FHWA does show similar systems without blockouts as NCHRP 350 approved. See the Structural Project Manager (SPM) or the Structural Liaison Engineer (SLE), if practical, to omit blockout. A design exception shall be required. Blockouts shall always be required on major routes.
There are four systems for use on state routes. In these four systems the connection design load used is 1.5 times plastic moment capacity (Mp) of W6 x 20 Post. The vertical clearance of System 3 shall be checked due to the obtruding lower connection.
| Bridge Standard Drawings |
| Thrie Beam Rails - THRIE |
751.40.4.4 End Treatment Using Thrie Beam Rail
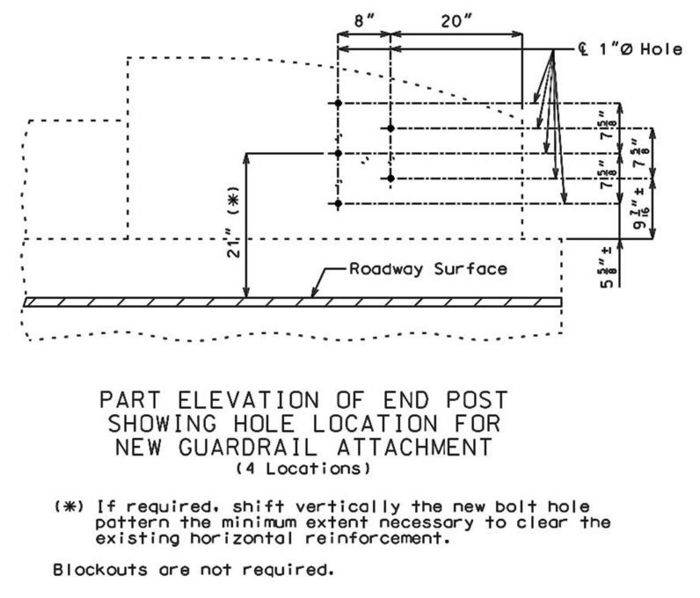
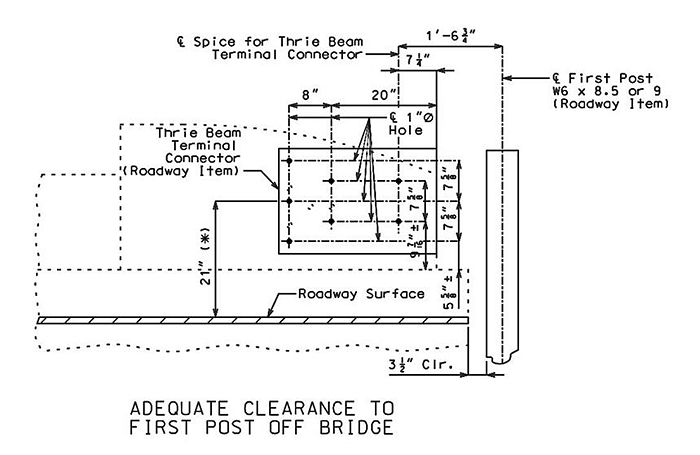
Guidance for Design:
- Adequate clearance to first post off bridge shall be required. (See also Standard Plan 617.10 for new bridges.)
751.40.4.5 Curb Blockouts
See EPG 751.1.3.4 Barrier or Railing Type, Height and Guidelines for Curb Blockouts for usage guidance.
| Bridge Standard Drawings |
| Barrier Modifications – BEM & CBO/Curb Blockouts - CBO |
751.40.5 Drainage
751.40.5.1 Structure with Wearing Surface Slab Drains - Details
Two material options may be used for slab drains:
- 1. Steel Slab Drains and inserts are only shown in the following details.
- 2. Fiberglass Reinforced Polymer (FRP) drains may be used with the approval of the Structural Project Manager or Structural Liaison Engineer. See EPG 751.10.3.2.1 New Structure Without Wearing Surface Slab Drains - Details for guidance and details of FRP drains on new structures as an aid.
- A positive mechanical connection must be used for attaching FRP drains to either existing steel drains or to new FRP inserts since welding cannot be used as is shown in the following details for steel drains. For example, using at least four bolt-through connectors (one per side) from new FRP drains into a new wearing surface or an existing steel drain, or using an epoxy adhesive in conjunction with at least two bolt-through connectors is required. It has been shown that using a more viscous epoxy or anchoring gel is beneficial in order to avoid dripping during placement. Using epoxy adhesive or an anchoring gel by itself is not acceptable.
- FRP drain may not fit exactly to the inside or to the outside of existing steel drain. The looseness of fit can be addressed by considering a combination of attachment details like mechanical connectors (to existing slab drain) plus either a viscous epoxy adhesive or a positive attachment to an exterior girder depending on the length of the slab drain extension.
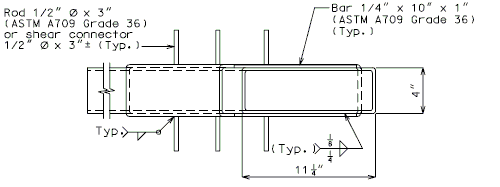
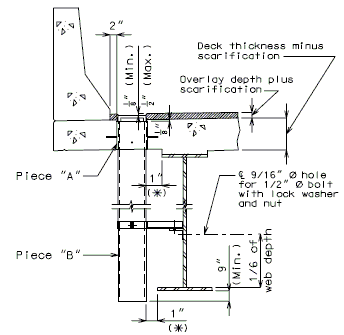
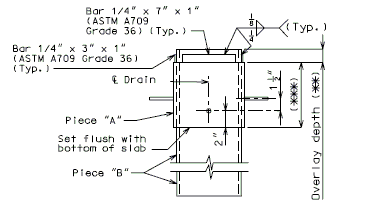
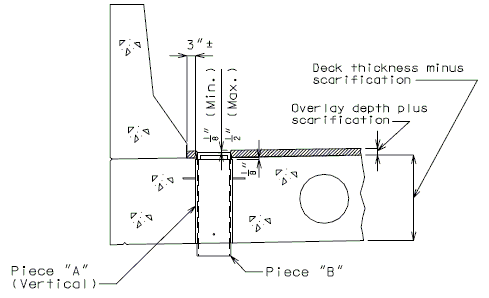
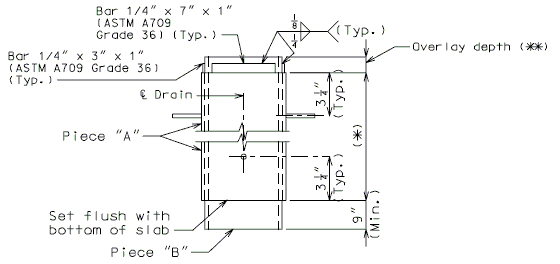
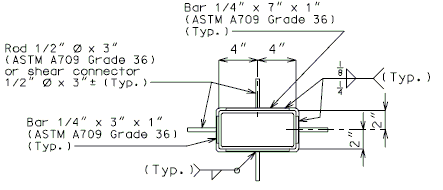
For new wearing surface over new slab, note on plans:
- Piece "A" shall be cast in the concrete slab. Prior to placement of wearing surface, piece "B" shall be inserted into piece "A".
FOR STRUCTURE WITH WEARING SURFACE
(GIRDER DEPTH LESS THAN 48")
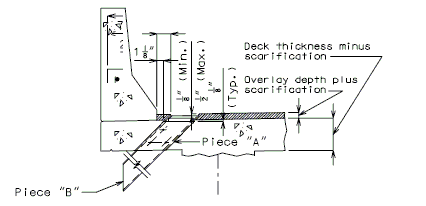
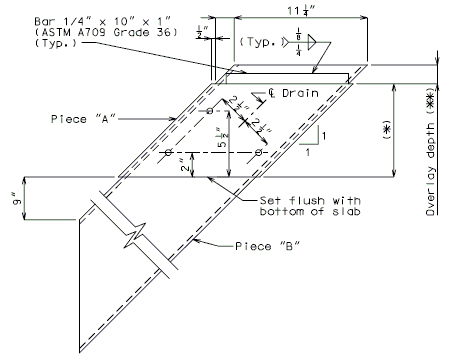
| * | Deck thickness minus 1/8" minus the depth of the scarification. |
| ** | Do not include the depth of the scarification. |
FOR STRUCTURE WITH WEARING SURFACE
(GIRDER DEPTH 48" AND OVER)
|
|
| ELEVATION OF DRAIN | |
| |
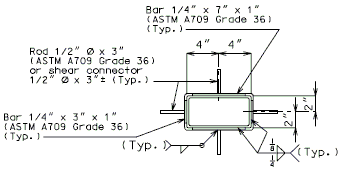
| PART ELEVATION OF SLAB AT DRAIN | PLAN OF DRAIN |
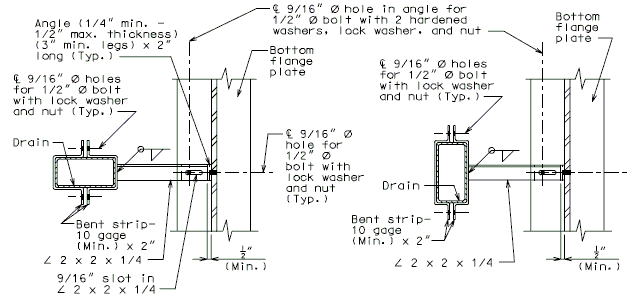
* If dimension is less than 1", drains shall be placed parallel to roadway. Otherwise, place drains transverse to roadway. ** Do not include the depth of the scarification. *** Deck thickness minus 1/8" minus the depth of the scarification.
| |
| DRAIN TRANSVERSE TO ROADWAY | DRAIN PARALLEL TO ROADWAY |
| PART PLANS SHOWING BRACKET ASSEMBLY | |
FOR STRUCTURE WITH WEARING SURFACE
(CONTINUOUS CONCRETE STRUCTURES)
| * | Deck thickness minus 1/8" minus the depth of the scarification. |
| ** | Do not include the depth of scarification. |
FOR STRUCTURE WITH WEARING SURFACE
(VARIABLE DEPTH GIRDERS)
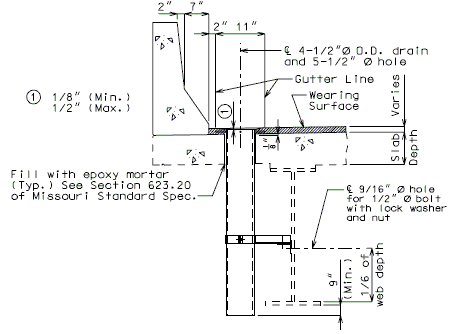
Note: For variable depth girders with drains in deeper section, let the deeper section control and use throughout the structure.
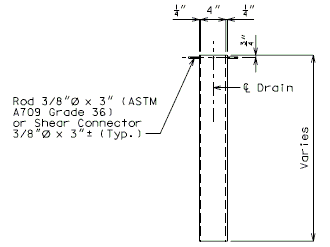
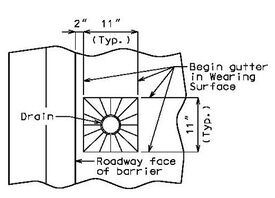
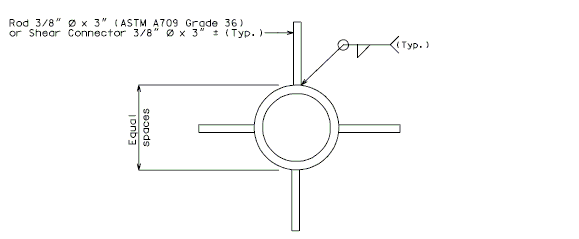
751.40.5.2 Structure with Wearing Surface Round Slab Drains - Details
FOR STRUCTURE WITH WEARING SURFACE
MISCELLANEOUS DETAILS - ROUND DRAINS
FRP round drains may be used optionally unless otherwise specified. See EPG 751.10.3 Bridge Deck Drainage – Slab Drains for guidance and details as an aid. Specify nominal pipe size as needed referencing ASTM D2996. Specify outer diameter based on nominal pipe size necessary for drainage for coring the correct size hole in deck.
Note: See EPG 751.10.3 Bridge Deck Drainage – Slab Drain for slab drain spacing.
 |
 |
| TYPICAL PART PLAN | SECTION SHOWING BRACKET ASSEMBLY |
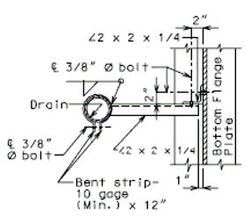
751.40.5.3 Structure with Wearing Surface Raising Slab Drains or Scuppers - Details
FOR STRUCTURE WITH WEARING SURFACE
RAISING SLAB DRAINS
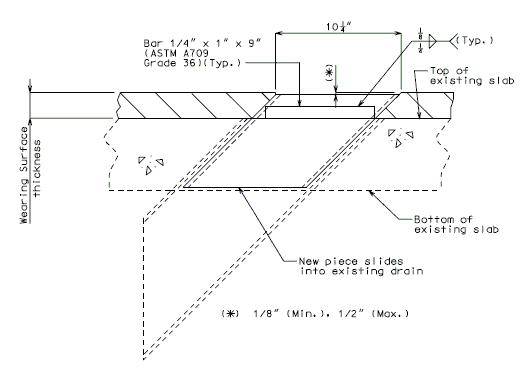
Outside dimensions of drain extension are 7-1/4" x 3-1/4", and drain extension shall be galvanized in accordance with ASTM A123.
FOR STRUCTURE WITH WEARING SURFACE
RAISING SCUPPERS
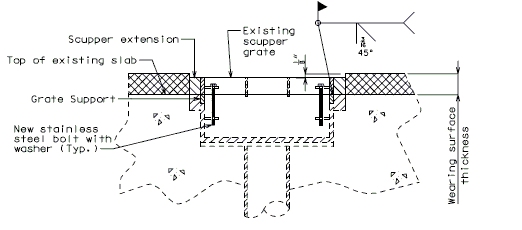
AND
PLAN OF SCUPPER EXTENSION
751.40.5.4 Cored Slab Drains
Cored slab drains may be installed in areas where the existing drainage is a concern, but the deck is not in need of replacement. Typically, 4-inch diameter drains are installed vertically to avoid the deck reinforcing steel which is typically spaced at 5-inch centers. If necessary, larger diameter drains or angled drains may be used with approval of the SPM or SLE.
| Bridge Standard Drawings |
| Rehabilitation, Surfacing & Widening - RHB/Cored Slab Drain for Existing Bridge Deck [RHB18] |
751.40.6 Closure Pour
Note:
For closure pour on solid slab or voided slab bridges, use expansive concrete.
Release the forms before the closure pour is placed.
751.40.7 Design and Posting Considerations
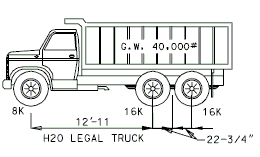
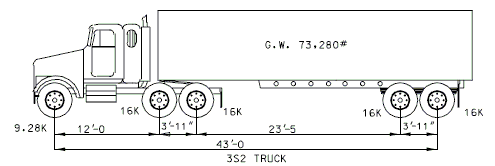
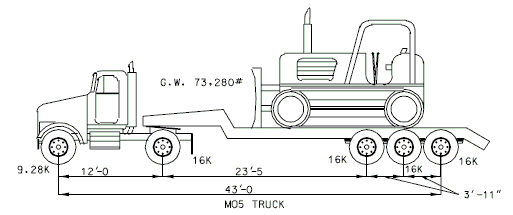
Existing structures to redecked and/or widened should be evaluated to determine if the superstructure is considered to be structurally adequate. The structural adequacy check should be determined based on load ratings using the Load Factor Method. Strengthening of the superstructure will not be required if the minimum posting values shown below meet or exceed legal load requirements. In addition, there may be cases where the existing bridge posting is acceptable based on the bridge specific site conditions such as AADT, amount of truck traffic, overweight permit route, etc.
| 1) | H20 (one lane with Impact) [Posting Rating] ≥ 23 tons |
| 2) | 3S2 (one lane with impact) [Posting Rating] ≥ 40 tons |
Posting Rating = 86% of Load Factor Operating Rating (Refer to figures below for H20, 3S2 and MO5 criteria).
If a structure is located within a commercial zone, then the following additional posting condition must be investigated:
| 3) | M05 (two lane with impact) [Operating Rating] ≥ 70 Tons (posting limit) |
Any other overstresses or inadequacies (slab, substructure, etc.) shall be reported to the Structural Project Manager.
Deck thickness for redecks shall be determined such that Posting will not be required or the existing posting is not lowered, and it is generally not less than original deck thickness.
Deck thickness for widenings shall be existing thickness unless thicker slab does not create overall deck stiffening irregularities.
See Structural Project Manager if AASHTO minimum deck thickness can not be used on redecks and widenings.
Future Wearing Surface (FWS) Loadings for widenings with concrete wearing surfaces - In addition to weight of wearing surface:
- Add FWS of 35 psf to the design of new girders if existing girders are sufficient for the 35 psf FWS
- Lower FWS loading to 15 psf if existing girders are not sufficient for FWS loading of 35 psf
- If existing girders are not sufficient for any FWS then lower FWS to FWS = 0.
- The existing ratings should be reviewed to determine what wearing surface loads were used. When necessary, the rating should be evaluated for acceptability of the proposed changes in the wearing surface loads and geometry. Preliminary ratings that are based on estimated geometry shall be revised when the updated, final geometry is known.
751.40.8 Design Information when using AASHTO Standard Specifications for Highway Bridges 17th Edition
751.40.8.1 Loadings
751.40.8.1.1 Live Load
Structures shall be designed to carry the dead load, live load, impact (or dynamic effect of the live load), wind load and other forces, when they are applicable.
Members shall be designed with reference to service loads and allowable stresses as provided in AASHTO (17th edition) Service Load Design Method (Allowable Stress Design) or with reference to factored load and factored strength as provided in AASHTO Strength Design Method (Load Factor Design). Load groups represent various combination of loads and forces to which a structure may be subjected. Group loading combinations for Service Load Design and Load Factor Design are given by AASHTO (17th edition) 3.22.1 and AASHTO (17th edition) Table 3.22.1A.
The live load shall consist of the applied moving load of vehicles and pedestrians. The design live load to be used in the design of bridges for the state system will be as stated on the Bridge Memorandum.
- The design truck: HS20-44 or HS20-44 Modified
- The design tandem (Military)
- The design lane loading
Criteria
- All widened or retrofitted bridges on the National Highway System and in commercial zones may be designed for HS20-44 Modified loading. All remaining bridges will be designed for HS20-44 loading.
- The Design Tandem loading is to be checked on national highway system or when Alternate Military loading appears on the Bridge Memorandum.
- Carrying members of each structure shall be investigated for the appropriate loading.
- Main carrying members include:
- Steel or Concrete stringers or girders.
- Longitudinally reinforced concrete slabs supported on transverse floor beams or substructure units (includes hollow slabs).
- Transversely reinforced concrete slabs supported by main carrying members parallel to traffic and over 8'-0" center to center. Use the formulas for moment in AASHTO Article 3.24.3.1 Case A.
- Steel grid floors when the main elements of the grid extend in a direction parallel to traffic, or with main elements transverse to traffic on supports more than 8'-0" apart.
- Timber floors and orthotropic steel decks.
- Main carrying members include:
- The reduction in live load for calculating substructure members is based on AASHTO 3.12.1. See Live Load Distribution in the Load Distribution Section.
HS20-44 Truck Loading
The HS20-44 truck is defined below as one 8 kip axle load and two 32 kip axle loads spaced as shown.
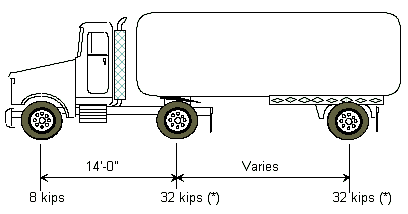
Varies = Variable spacing 14’ to 30’ inclusive. Spacing to be used is that which produces the maximum stresses.
(*) In the design of timber floors and orthotropic steel decks (excluding transverse beams) for H-20 Loading, one axle load of 24 kips or two axle loads of 16 kip each, spaced 4 feet apart may be used, whichever produces the greater stress, instead of the 32 kip axle load shown.
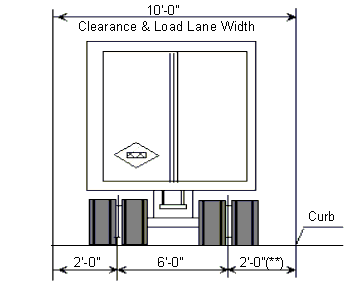
(**) For slab design, the center line of wheels shall be assumed to be one foot from face of cur
HS20-44 Modified Truck Loading
The HS20-44 Modified truck is defined below as one 10 kip axle load and two 40 kip axle loads spaced as shown. This is the same as HS20-44 truck modified by a factor of 1.25.
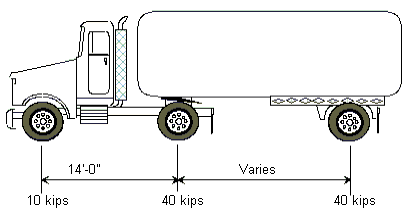
Varies = Variable spacing 14’ to 30’ inclusive. Spacing to be used is that which produces the maximum stresses.
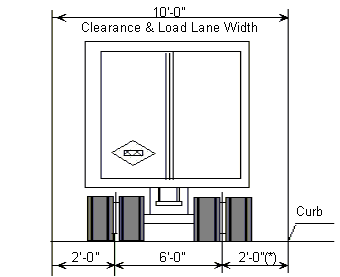
(*) For slab design, the center line of wheels shall be assumed to be one foot from face of curb.
Design Tandem Loading
The Design Tandem Loading is a two axle load each of 24 kips. These axles are spaced at 4'-0" centers. The transverse spacing of wheels shall be taken as 6'-0".
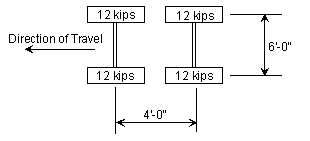
Design Lane Loading
- For HS20-44 Truck, the design lane load shall consist of a load 640 lbs per linear foot, uniformly distributed in the longitudinal direction with a single concentrated load (or two concentrated loads in case of continuous spans for determination of maximum negative moment), so placed on the span as to produce maximum stress. The concentrated load and uniform load shall be considered as uniformly distributed over a 10'-0" width on a line normal to the center line of the lane.
- For HS20-44 Modified Truck, use the HS20-44 truck modified by a factor of 1.25.
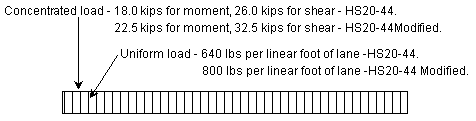
- For the design of continuous structures, an additional concentrated load is placed in another span to create the maximum effect. For positive moments, only one concentrated load is used, combined with as many spans loaded uniformly as are required to produce the maximum moment.
Standard Roadway Width
- 26'-0" (up to 2 traffic lanes)
- 28'-0" (up to 2 traffic lanes)
- 30'-0" (up to 3 traffic lanes)
- 32'-0" (up to 3 traffic lanes)
- 36'-0" (up to 3 traffic lanes)
- 38'-0" (up to 3 traffic lanes)
- 40'-0" (up to 4 traffic lanes)
- 44'-0" (up to 4 traffic lanes)
751.40.8.1.2 Impact
Highway live loads shall be increased by a factor given by the following formula:
in feet
For continuous spans, to be used in this equation for negative moments is the average of two adjacent spans at an intermediate bent or the length of the end span at an end bent. For positive moments, is the span length from center to center of support for the span under consideration.
Impact is never to be more than 30 percent. It is intended that impact be included as part of the loads transferred from superstructure to substructure but not in loads transferred to footings or parts of substructure that are below the ground line. The design of neoprene bearing pads also does not include impact in the design loads.
751.40.8.1.3 Collision Force
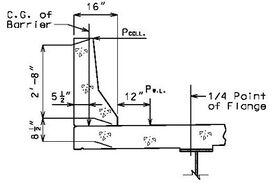
Collision forces shall be applied to the barrier or railing in the design of the cantilever slab. A force of 10 kips is to be applied at the top of the standard barrier or railing. This force is distributed through the barrier or railing to the slab.
751.40.8.1.4 Centrifugal Force
Structures on curves shall be designed for a horizontal radial force equal to the following percentage of the live load in all the lanes, without impact.
Where:
| = the centrifugal force in percent of the live load | |
| = the design speed in miles per hour | |
| = the radius of the curve in feet |
This force shall be applied at 6 feet above the centerline of the roadway with one design truck being placed in each lane in a position to create the maximum effect. Lane loads shall not be used in calculating centrifugal forces.
The effects of superelevation shall be taken into account.
751.40.8.1.5 Lateral Earth Pressure
Structures which retain fills shall be designed for active earth pressures as
Where:
| = active earth pressure per length (lb/ft) | ||
| = unit weight of the back fill soil = 120 lb/ft³ | ||
| = coefficient of active earth pressure as given by Rankine’s formula | ||
| = | = equivalent fluid pressure (lb/ft³)(*) | |
| = height of the back fill soil (ft) | ||
Rankine's Formula
The coefficient of active earth pressure is:
Where:
| = angle of internal friction of the backfill soil (*) | |
| = the angle of incline of the backfill |
If the backfill surface is level, angle a is zero and is:
(*) Use the internal friction angle indicated on the Bridge Memorandum. However, if the friction angle is not determined, use the minimum equivalent fluid pressure value, , of 45 lb/ft³ for bridges and retaining walls. For box culverts use a maximum of 60 lb/ft³ and a minimum of 30 lb/ft³ for fluid pressure.
Live Load Surcharge
An additional earth pressure shall be applied to all structures which have live loads within a distance of half the structure height. This additional force shall be equal to adding 2'-0" of fill to that presently being retained by the structure.
751.40.8.1.6 Longitudinal Forces (Braking Forces)
A longitudinal force of 5% of the live load shall be applied to the structure. This load shall be 5% of the lane load plus the concentrated load for moment applied to all lanes and adjusted by the lane reduction factor. Apply this force at 6 feet above the top of slab and to be transmitted to the substructure through the superstructure.
751.40.8.1.7 Wind Load
Wind loads shall be applied to the structure regardless of length.
The pressure generated by wind load is:
Where:
| = wind pressure in pounds per square foot | |
| = design wind velocity = 100 miles per hour | |
| = 0.004 for wind load |
Basic wind load (pressure) = 0.004 x (100)² = 40 lb/ft²
Wind Load for Superstructure Design
Transverse
A wind load of the following intensity shall be applied horizontally at right angles to the longitudinal axis of the structure.
- Trusses and Arches = 75 pounds per square foot =
- Girders and Beams = 50 pounds per square foot (*) = (for plate girder lateral bracing check only)
- The total force shall not be less than 300 pounds per linear foot in the plane of windward chord and 150 pounds per linear foot in the plane of the leeward chord on truss spans, and not less than 300 pounds per linear foot on girder spans.
Wind Load for Substructure Design
Forces transmitted to the substructure by the superstructure and forces applied directly to the substructure by wind load shall be as follows:
Forces from Superstructure: Wind on Superstructure
Transverse
A wind load of the following intensity shall be applied horizontally at right angles to the longitudinal axis of the structure.
- Trusses and Arches = 75 pounds per square foot =
- Girders and Beams = 50 pounds per square foot (*) =
(*) Use Wt = 60 lbs/ft² for design wind force on girders and beams If the column height on a structure is greater than 50 feet, where the height is the average column length from ground line to bottom of beam.
The transverse wind force for a bent will be:
Where:
| = length in feet = the average of two adjacent spans for intermediate bents and half of the length of the end span for end bents. | |
| = the total height of the girders, slab, barrier or raling and any superelevation of the roadway, in feet | |
| = wind force per unit area in pounds per square foot |
This transverse wind force will be applied at the top of the beam cap for the design of the substructure.
Longitudinal (**)
The standard wind force in the longitudinal direction shall be applied as a percentage of the transverse loading. Use approximately 25%.
Truss and Arch Structures = 75 x 0.25 = approximately 20 lbs/ft² Girder Structures = 50 x 0.25 = approximately 12 lbs/ft²
The total longitudinal wind force will be:
Where:
| = the overall bridge length in feet | |
| = the total height of the girders, slab, barrier or railing and anysuperelevation of the roadway, in feet | |
| = wind force per unit area in pounds per square foot |
This longitudinal force is distributed to the bents based on their stiffness. (**)
The longitudinal wind force for the bent will be applied at the top of the beam cap for the design of the substructure.
Forces from Superstructure: Wind on Live Load
A force of 100 pounds per linear foot of the structure shall be applied transversely to the structure along with a force of 40 pounds per linear foot longitudinally. These forces are assumed to act 6 feet above the top of slab. The transverse force is applied at the bents based on the length of the adjacent spans affecting them. The longitudinal force is distributed to the bents based on their stiffness. (**)
(**) See EPG 751.2.4.6 Longitudinal Wind Force Distribution.
Forces Applied Directly to the Substructure
The transverse and longitudinal forces to be applied directly to the substructure elements shall be calculated from an assumed basic wind force of 40 lbs/ft². This wind force per unit area shall be multiplied by the exposed area of each substructure member in elevation (use front view for longitudinal force and side view for transversely force, respectively). These forces are acting at the center of gravity of the exposed portion of the member.
A shape factor of 0.7 shall be used in applying wind forces to round substructure members.
When unusual conditions of terrain or the special nature of a structure indicates, a procedure other than the Standard Specification may be used subject to approval of the Structural Project Manager.
751.40.8.1.8 Temperature Forces
Temperature stresses or movement need to be checked on all structures regardless of length. Generation of longitudinal temperature forces is based on stiffness of the substructure. (*)
Coefficients
Steel: Thermal - 0.0000065 ft/ft/°F Concrete: Thermal - 0.0000060 ft/ft/°F Shrinkage - 0.0002 ft/ft (***) Friction - 0.65 for concrete on concrete
| Rise | Fall | Range | |
| Steel Structures | 60°F | 80°F | 140°F |
| Concrete Structures | 30°F | 40°F | 70°F |
(*) See EPG 751.2.4.7 Longitudinal Temperature Force Distribution.
(**) Temperature Range for expansion bearing design and expansion devices design see EPG 751.11 Bearings and EPG 751.13 Expansion Devices, respectively.
(***) When calculating substructure forces of concrete slab bridges, the forces caused by the shrinkage of the superstructure should be included with forces due to temperature drop. This force can be ignored for most other types of bridges.
751.40.8.1.9 Sidewalk Loading
Sidewalk floors and their immediate support members shall be designed for a live load of 85 pounds per square foot of sidewalk area. Girders, trusses, and other members shall be design for the following sidewalk live load:
Spans 0 to 25 feet 85 lbs/ft² Spans 26 to 100 feet 60 lbs/ft² Spans over 100 feet use the following formula
Where:
| = live load per square foot, max. 60 lbs/ft² | |
| = loaded length of sidewalk in feet | |
| = width of sidewalk in feet |
When sidewalk live loads are applied along with live load and impact, if the structure is to be designed by service loads, the allowable stress in the outside beam or stringer may be increased by 25 percent as long as the member is at least as strong as if it were not designed for the additional sidewalk load using the initial allowable stress. When the combination of sidewalk live load and traffic live load plus impact governs the design under the load factor method, use a b factor of 1.25 instead of 1.67.
Unless a more exact analysis can be performed, distribution of sidewalk live loads to the supporting stringers shall be considered as applied 75 percent to the exterior stringer and 25 percent to the next stringer.
751.40.8.1.10 Other Loads
Stream Pressure
Stream flow pressure shall be considered only in extreme cases. The affect of flowing water on piers shall not be considered except in cases of extreme high water and when the load applied to substructure elements is greater than that which is applied by wind on substructure forces at low water elevations.
The pressure generated by stream flow is:
Where:
| = stream pressure in pounds per square foot | |
| = design velocity of water in feet per second | |
| = shape constant for the surface the water is in contact with. | |
| = 1.4 for square-ended piers | |
| = 0.7 for circular piers | |
| = 0.5 for angle-ended piers where the angle is 30 degrees or less |
Ice Forces
Ice forces on piers shall be applied if they are indicated on the Bridge Memorandum.
Buoyancy
Buoyancy shall be considered when its effects are appreciable.
Fatigue in Structural Steel
Steel structures subjected to continuous reversal of loads are to be designed for fatigue loading.
Prestressing
See EPG 751.22 P/S Concrete I Girders.
Other Loads
Other loads may need to be applied if they are indicated on the Bridge Memorandum. Otherwise see Structural Project Manager before applying any additional loads.
751.40.8.1.11 Group Loads
Group Loading (Service Load Design)
Group loading combinations are:
GP I SL 100% GP II SL 125% GP III SL 125% GP IV SL 125% GP V SL 140% GP VI SL 140%
Where:
| = dead load | |
| = live load | |
| = live load impact | |
| = wind load on structure | |
| = wind load on live load | |
| = temperature force | |
| = longitudinal force from live load |
Group Loading (Load Factor Design)
Group loading combinations are:
GP I LF GP II LF GP III LF GP IV LF GP V LF GP VI LF
Where:
| = dead load | |
| = live load | |
| = live load impact | |
| = wind load on structure | |
| = wind load on live load | |
| = temperature force | |
| = longitudinal force from live load | |
| = coefficient, see AASHTO Table 3.22.1A |
Other group loadings in AASHTO Table 3.22.1A shall be used when they apply.
751.40.8.2 Distribution of Loads
751.40.8.2.1 Distribution of Dead Load
Composite Steel or Prestressed Concrete Structures
The dead load applied to the girders through the slab shall be:
Dead Load 1
Non-composite dead loads should be distributed to girders (stringers) on the basis of continuous spans over simple supports.
Dead Load 2
Composite loads shall be distributed equally to all girders. The following are all Dead Load 2 loads:
- Barrier or railing
- Future wearing surface on slab
- Sidewalks
- Fences
- Protective coatings and waterproofing on slab
Concrete Slab Bridges
Distribute entire dead load across full width of slab.
For longitudinal design, heavier portions of the slab may be considered as concentrated load for entry into the "Continuous Structure Analysis" computer program.
For transverse bent design, consider the dead load reaction at the bent to be a uniform load across entire length of the transverse beam.
751.40.8.2.2 Distribution of Live Load
Live loading to be distributed shall be the appropriate loading shown on the Bridge Memorandum. Applying Live Load to Structure
Superstructure
For application of live load to superstructure, the lane width is considered 12 feet. Each design vehicle has wheel lines which are 6 feet apart and adjacent design vehicles must be separated by 4 feet.
Substructure
To produce the maximum stresses in the main carrying members of substructure elements, multiple lanes are to be loaded simultaneously. The lane width is 12 feet. Partial lanes are not to be considered. Due to the improbability of coincident maximum loading, a reduction factor is applied to the number of lanes. This reduction however, is not applied in determining the distribution of loads to the stringers.
| Number of Lanes | Percent |
|---|---|
| one or two lanes | 100 |
| three lanes | 90 |
| four lanes or more | 75 |
Moment Distribution
Moments due to live loads shall not be distributed longitudinally. Lateral distribution shall be determined from AASHTO Table 3.23.1 for interior stringers. Outside stringers distribute live load assuming the flooring to act as a simple span, except in the case of a span with a concrete floor supported by four or more stringers, then AASHTO 3.23.2.3.1.5 shall be applied. In no case shall an exterior stringer have less carrying capacity than an interior stringer.
Shear Distribution
As with live load moment, the reactions to the live load are not to be distributed longitudinally. Lateral distribution of live load shall be that produced by assuming the flooring to act as simply supported. Wheel lines shall be spaced on accordance with AASHTO 3.7.6 and shall be placed in a fashion which provides the most contribution to the girder under investigation, regardless of lane configuration. The shear distribution factor at bents shall be used to design bearings and bearing stiffeners.
Deflection Distribution
Deflection due to live loads shall not be distributed longitudinally. Lateral distribution shall be determined by averaging the moment distribution factor and the number of wheel lines divided by the number of girder lines for all girders. The number of wheel lines shall be based on 12 foot lanes. The reduction in load intensity (AASHTO Article 3.12.1) shall not be applied.
Deflection Distribution Factor =
Where:
| = number of whole 12 foot lanes on the roadway | |
| = number of girder lines; | |
| = Moment Distribution Factor. |
Example: 38'-0" Roadway (Interior Girder), , ,
Deflection Distribution Factor =
| Roadway Width |
Number Girders |
Girder Spacing |
Exterior Girder | Interior Girder | (1) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mom. | Shear | Defl. | Mom. | Shear | Defl. | ||||
| 26’-0” | 4 | 7’-6” | 1.277 | 1.133 | 1.139 | 1.364 | 1.667 | 1.182 | 1.071 |
| 28’-0” | 4 | 8’-2” | 1.352 | 1.204 | 1.176 | 1.485 | 1.776 | 1.243 | 1.167 |
| 30’-0” | 4 | 8’-8” | 1.405 | 1.308 | 1.453 | 1.576 | 1.846 | 1.538 | 1.238 |
| 32’-0” | 4 | 9’-2” | 1.457 | 1.400 | 1.479 | 1.667 | 1.909 | 1.584 | 1.310 |
| 36’-0” | 5 | 8’-2” | 1.352 | 1.184 | 1.276 | 1.485 | 1.776 | 1.343 | 1.167 |
| 38’-0” | 5 | 8’-8” | 1.405 | 1.231 | 1.303 | 1.576 | 1.846 | 1.388 | 1.238 |
| 40’-0” | 5 | 9’-0” | 1.440 | 1.333 | 1.520 | 1.636 | 1.889 | 1.618 | 1.286 |
| 44’-0” | 5 | 9’-9” | 1.515 | 1.487 | 1.558 | 1.773 | 1.974 | 1.687 | 1.393 |
Distribution of Live Load to Substructure
For substructure design the live load wheel lines shall be positioned on the slab to produce maximum moments and shears in the substructure. The wheel lines shall be distributed to the stringers on the basis of simple spans between stringers. The number of wheel lines used for substructure design shall be based on 12 foot lanes and shall not exceed the number of lanes times two with the appropriate percentage reduction for multiple lanes where applicable.
In computing these stresses generated by the lane loading, each 12 foot lane shall be considered a unit. Fractional units shall not be considered.
Distribution of Loads to Slabs
For simple spans, the span length shall be the distance center to center of supports but need not be greater than the clear distance plus the thickness of the slab. Slabs for girder and floor beam structures should be designed as supported on four sides.
For continuous spans on steel stringers or on thin flanged prestressed beams (top flange width to thickness ratios > 4.0), the span length shall be the distance between edges of top flanges plus one quarter of each top flange width. When the top flange width to thickness is < 4.0 the span distance shall be the clear span between edges of the top flanges.
When designing the slab for live load, the wheel line shall be placed 1 foot from the face of the barrier or railing if it produces a greater moment.
Bending Moments in Slab on Girders
The load distributed to the stringers shall be:
P20 or P25 = Moment in foot-pounds per-foot width of slab.
Where:
| = effective span length between girders in feet | |
| P20 or P25 | = wheel line load for HS20 or HS20 Modified design Truck in kips. |
For slabs continuous over 3 or more supports, a continuity factor of 0.8 shall be applied.
Main Reinforcement Parallel to Traffic
This distribution may be applied to special structure types when its use is indicated.
Distribution of Live Load to Concrete Slab Bridges
Live load for transverse beam, column and pile cap design shall be applied as concentrated loads of one wheel line. The number of wheel lines used shall not exceed the number of lanes x 2 with the appropriate reduction where applicable.
For slab longitudinal reinforcement design, use live load moment distribution factor of 1/E for a one-foot strip slab with the appropriate percentage reduction.
Where:
| = Width of slab in feet over which a wheel is distributed | |
| = Effective span length in feet. |
For slab deflection, use the following deflection factor for a one-foot strip slab without applying percentage reduction.
Deflection Factor = (Total number of wheel line) / (width of the slab)
751.40.8.2.3 Frictional Resistance
The frictional resistance varies with different surfaces making contact. In the design of bearings, this resistance will alter how the longitudinal forces are distributed. The following table lists commonly encountered materials and their coefficients. These coefficients may be used to calculate the frictional resistance at each bent.
| Frictional Resistance of Expansion Bearings | |||
|---|---|---|---|
| Bearing Type | Coef. | General Data | |
| Type C Bearing | 0.14 | Coef. of sliding friction steel to steel = 0.14
Coef. for pin and rocker
Frictional Force = | |
| 6” Diameter Roller | 0.01 | ||
| Type D Bearing | |||
| Pin Diameter | Rocker Radius | ||
| 2” | 6.5” | 0.0216 | |
| 2” | 7” | 0.0200 | |
| 2” | 7.5” | 0.0187 | |
| 2” | 8” | 0.0175 | |
| 2” | 10.5” | 0.0133 | |
| PTFE Bearing | 0.0600 | ||
The design of a bent with one of the above expansion bearings will be based on the maximum amount of load the bearing can resist by static friction. When this static friction is overcome, the longitudinal forces are redistributed to the other bents.
The maximum static frictional force at a bent is equal to the sum of the forces in each of the bearings. The vertical reaction used to calculate this maximum static frictional force shall be Dead Loads only for all loading cases. Since the maximum longitudinal load that can be experienced by any of the above bearings is the maximum static frictional force, the effects of longitudinal wind and temperature can not be cumulative if their sum is greater than this maximum static frictional force.
Two conditions for the bents of the bridge are to be evaluated.
- Consider the expansion bents to be fixed and the longitudinal loads distributed to all of the bents.
- When the longitudinal loads at the expansion bearings are greater than the static frictional force, then the longitudinal force of the expansion bearings is equal to the dynamic frictional force. It is conservative to assume the dynamic frictional force to be zero causing all longitudinal loads to be distributed to the remaining bents.
751.40.8.3 Unit Stresses
751.40.8.3.1 Fatigue in Structural Steel
Steel structures subjected to continuous reversal of loads are to be designed for fatigue loading.
AADTT, annual average daily truck traffic (one direction), shall be indicated on the Bridge Memorandum. Based on AADTT, the fatigue case and corresponding stress cycles can be obtained from AASHTO Table 10.3.2A.
When Case I fatigue is considered, it is necessary to check fatigue due to truck loading for both the 2,000,000 and over 2,000,000 stress cycles. For the over 2,000,000 stress cycles, the moment distribution factor for all stringers or girders (for fatigue stresses only) will be based on one lane loaded. For truck loading 2,000,000 cycles and lane loading 500,000 cycles, use the moment distribution factor based on two or more traffic lanes (same as for design moment).
The number of cycles to be used in the fatigue design is dependent on the case number and type of load producing maximum stress as indicated in AASHTO Table 10.3.2A. The allowable fatigue stress range based on the fatigue stress cycles can be obtained from AASHTO Table 10.3.1A.
The type of live load used to determine the number of cycles will be the type of loading used to determine the maximum stress at the point under consideration.
In continuous beams, the maximum stresses may be produced by the truck loading at some points, but by lane loading at other points. However, if the lane loading governs, then the longitudinal members should also be checked for truck loading.
Only live loading and impact stresses need to be considered when designing for fatigue.
Fatigue criteria applies only when the stress range is one of tension to tension or reversal. The fatigue criteria does not apply to the stress range from compression to compression.
All fracture critical structures, those which consist of only one or two main carrying members, trusses or single box girders, shall be considered as Non-redundant structures. Use the appropriate table which accompanies these structures.
751.40.8.3.2 Reinforced Concrete
Allowable Stresses of Reinforcing Steel
Tensile stress in reinforcement at service loads, :
| Concrete | ||
|---|---|---|
| Reinforcing Steel (Grade 40) | = 20,000 psi | |
| Reinforcing Steel (Grade 60) | = 24,000 psi | |
For compression stress in beams, see AASHTO Article 8.15.3.5.
For compression stress in columns, see AASHTO Article 8.15.4.
For fatigue stress limit, see AASHTO Article 8.16.8.3.
Fatigue in Reinforcing Steel
For flexural members designed with reference to load factors and strengths by Strength Design Method, stresses at service load shall be limited to satisfy the requirements for fatigue. Reinforcement should be checked for fatigue at all locations of peak service load stress ranges and at bar cut-off locations except for concrete deck slab in multi-girder applications.
Allowable Stress Range:
The allowable stress range is found using the equation listed below and the minimum stresses from dead load, live load, and impact based on service loads.
The term minimum stress level fmin for this formula indicates the algebraic minimum stress level: tension stress with a positive sign and compression stress with a negative sign.
Where:
| = allowable stress range (ksi) | |
| = algebraic minimum stress level ksi): | |
| positive if tension, negative if compression. | |
| = ratio of base radius to height of rolled-on transverse deformation; if the actual value is not know, 0.3 may be used. | |
| = when |
Fatigue research has shown that increasing minimum tensile stress results in a decrease in fatigue strength for a tension to tension stresses case. The fatigue strength increases with a bigger compressive stress in a tension to compression stresses case.
Actual Stress Range:
The actual stress range, , is found using dead load, live load, and impact from service loads.
| = | ||
| = greatest tension stress level (ksi), always positive. | ||
| (Not necessary to check compression to compression for fatigue.) | ||
| = algebraic least stress level (ksi): | ||
| = positive if the least stress is tension | ||
| (tension to tension stresses) | ||
| = negative if the least stress is compression | ||
| (tension to compression stresses) | ||
Tension and Compression Stress Computation
Tension and compression stress are determined by using the following formulae for double reinforced concrete rectangular beams.
= tensile stress in reinforcement at service loads (ksi)
- Tensile stress
= compressive stress in reinforcement at service loads (ksi)
- Compressive stress
Where:
Eq. 2.2-1
Eq. 2.2-2
| = tension reinforcement ratio, | |
| = compression reinforcement ratio, | |
| = area of tension reinforcement (sq. inch) | |
| = area of compression reinforcement (sq. inch) | |
| = width of beam (inch) | |
| = distance from extreme compression fiber to centroid of tension reinforcement (inch) | |
| = distance from extreme compression fiber to centroid of compression reinforcement (inch) | |
| = distance from tensile steel to resultant compression (inch) | |
| = distance from neutral plane to compression surface (inch) | |
| = ratio of modulus of elasticity of steel to that of concrete |
751.40.8.4 Standard Details
751.40.8.4.1 Welding Details
All welding shall be detailed in accordance with ANSI / AASHTO / AWS D1.5, Bridge Welding Code.
For ASTM A709, Grade 36 steel (Service Load Design = 58,000 psi) the allowable shear stress in fillet welds () is:
Where:
| = allowable basic shear stress | |
| = tensile strength of the electrode classification but not greater than the tensile strength of the connected part |
| Size of Fillet Weld (Inch) |
Allowable Shear Loads per Length (Pound per lineal inch) |
| 1/8” | 1,380 |
| 3/16” | 2,075 |
| 1/4" | 2,770 |
| 5/16” | 3,460 |
| 3/8” | 4,150 |
| 1/2" | 5,535 |
| 5/8” | 6,920 |
| 3/4" | 8,300 |
| 7/8” | 9,690 |
| 1” | 11,070 |
(*) Allowable Shear Load =
Where:
| = Effective Length, in inch | |
| = Effective Throat, in inch | |
| = Effective weld area in sq. inch |
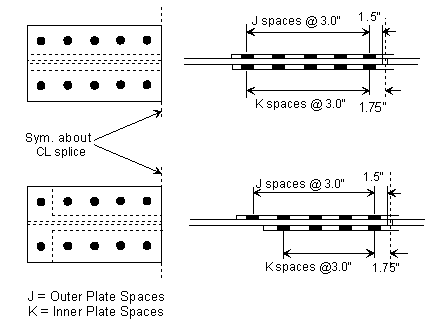
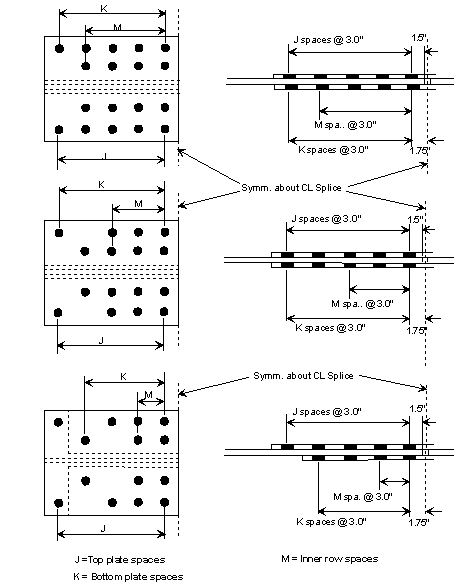
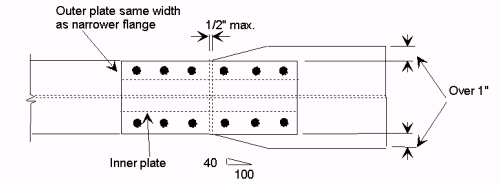
751.40.8.4.2 Development and splicing of Reinforcement
751.40.8.4.2.1 General
Development of Tension Reinforcement
Development lengths for tension reinforcement shall be calculated in accordance with AASHTO Article 8.25. Development length modification factors described in AASHTO Articles 8.25.3.2 and 8.25.3.3 shall only be used in situations where development length without these factors is difficult to attain. All other modification factors shown shall be used.
Development lengths for tension reinforcement have been tabulated on the following pages and include the modification factors except those described above.
Lap Splices of Tension Reinforcement
Lap splices of reinforcement in tension shall be calculated in accordance with AASHTO Article 8.32.1 and 8.32.3. Class C splices are preferred when possible, however it is permissible to use Class A or B when physical space is limited. The designer shall satisfy AASHTO Table 8.32.3.2 when using Class A or B splices. It should be noted that As required is based on the stress encountered at the splice location, which is not necessarily the maximum stress used to design the reinforcement.
Temperature and shrinkage reinforcement is assumed to fully develop the specified yield stresses. Therefore the development length shall not be reduced by ( required)/( supplied).
Splice lengths for tension reinforcement have been tabulated on the following pages and include the development length modifications as described above.
Development of Tension Hooks
Development of tension hooks shall be calculated in accordance with AASHTO Article 8.29. Hook length modification factors described in Articles 8.29.3.3 and 8.29.3.4 shall only be used in situations where hook length without these factors is difficult to attain. All other modification factors shown shall be used.
Development lengths of tension hooks have been tabulated on the following pages and include the modification factors except those described above.
Development of Compression Reinforcement
Development lengths for compression reinforcement shall be calculated in accordance with AASHTO Article 8.26. Development length modification factors described in AASHTO Articles 8.26.2.1 and 8.26.2.2 shall only be used in situations where development length without these factors is difficult to attain. All other modification factors shown shall be used.
Development lengths for compression reinforcement have been tabulated on the following pages and include the modification factors except those described above.
Lap Splices of Compression Reinforcement
Lap splices of reinforcement in compression shall be calculated in accordance with AASHTO Article 8.32.1 and 8.32.4.
Splice lengths for compression reinforcement have been tabulated on the following pages.
Mechanical Bar Splices
Mechanical bar splices may be used in situations where it is not possible or feasible to use lap splices. Mechanical bar splices shall meet the criteria of AASHTO Article 8.32.2. Refer to the manufacturers literature for more information on the design of mechanical bar splices.
751.40.8.4.2.2 Development and Tension Lap Splice Lengths - Top Bars (Fy = 60 ksi)
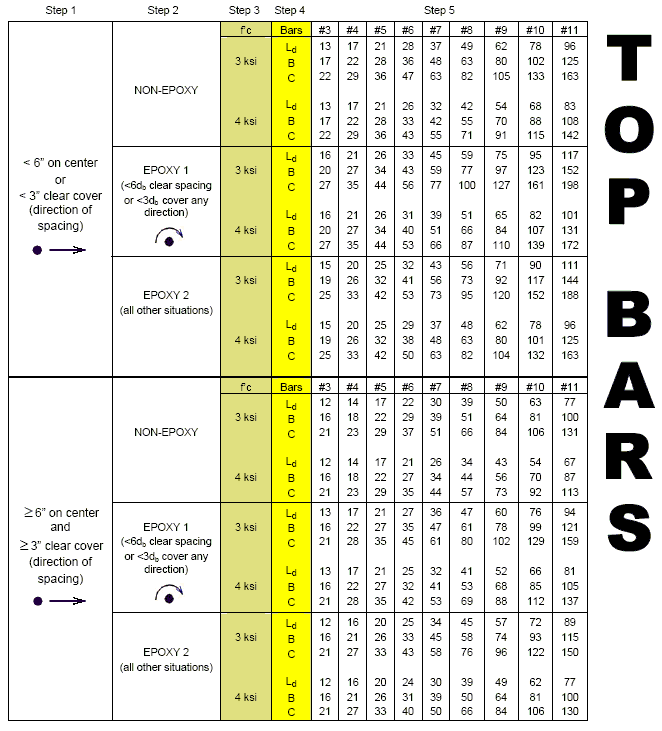
Top reinforcement is placed so that more than 12” of concrete is cast below the reinforcement.
Class A splice =1.0 , Class B splice =1.3 , Class C splice =1.7
Use development and tension lap splices of = 4 ksi for concrete strengths greater than 4 ksi.
751.40.8.4.2.3 Development and Tension Lap Splice Lengths - Other Than Top Bars (Fy = 60 ksi)
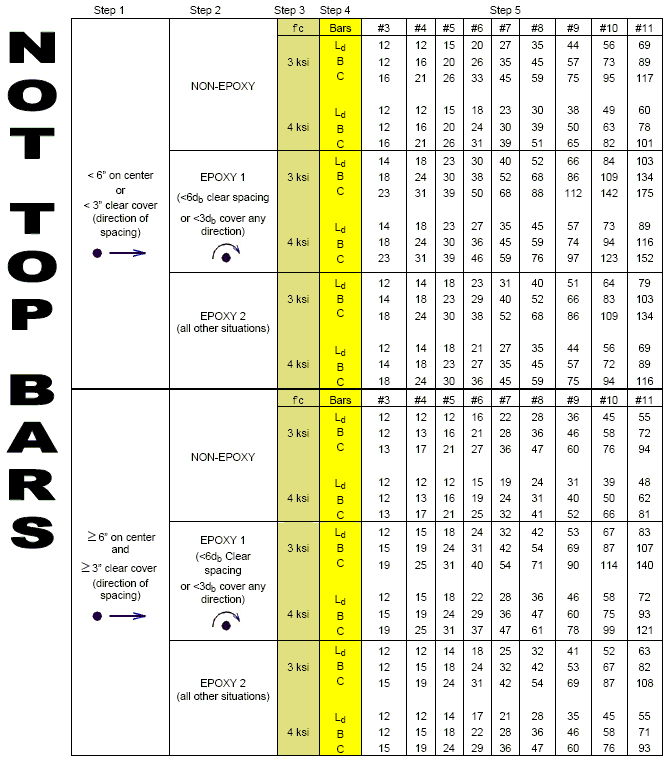
Class A splice =1.0 , Class B splice =1.3 , Class C splice =1.7
Use development and tension lap splices of = 4 ksi for concrete strengths greater than 4 ksi.
751.40.8.4.2.4 Development and Lap Splice Lengths - Bars in Compression (Fy = 60 ksi)
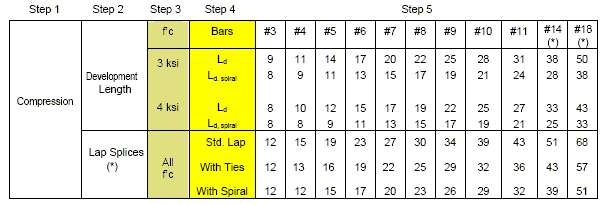
Development length for spirals, , , should be used if reinforcement is enclosed in a spiral of not less than 1/4” diameter and no more than 4” pitch. See AASHTO 8.26 for special conditions.
All values are for splices with the same size bars. For different size bars, see AASHTO 8.32.4.
(*) Lap splices for #14 and #18 bars are not permitted except as column to footing dowels.
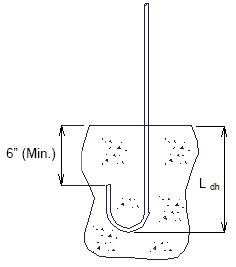
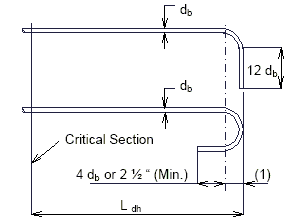
751.40.8.4.2.5 Development of Standard Hooks in Tension, Ldh (Fy = 60 ksi)
The development length, , is measured from the critical section to the outside edge of hook. The tabulated values are valid for both epoxy and uncoated hooks.
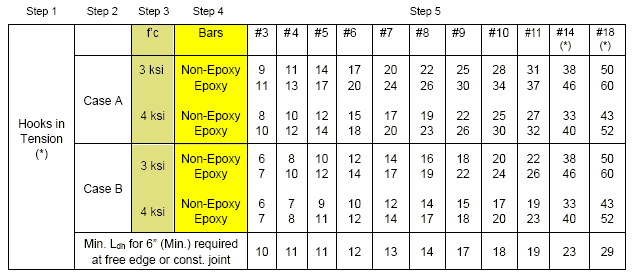
Case A - For #11 bar and smaller, side cover (normal to plane of hook) less than 2 1/2 inches and for a 90 degree hook with cover on the hook extension less than 2 inches.
Case B - For #11 bar and smaller, side cover (normal to plane of hook) greater than 2 1/2 inches and for a 90-dgree hook with cover on the hook extension 2 inches or greater.
(*) See Structural Project Manager before using #14 or #18 hook.
|
| |
| (1) = (#3 thru #8) | ||
| (1) = (#9, #10 and #11) | ||
| (1) = (#14 and #18) | ||
| DETAILS NEAR FREE EDGE OR CONSTRUCTION JOINT |
HOOKED-BAR DETAILS FOR DEVELOPMENT OF STANDARD HOOKS |
|---|
751.40.8.4.2.6 Development of Uncoated Grade 40 Deformed Bars in Tension, Ld (AASHTO 8.25)
| Bar | = 3 ksi | = 4 ksi | = 5 ksi | |||
|---|---|---|---|---|---|---|
| Top bar | Top bar | Top bar | ||||
| #3 | 12 | 12 | 12 | 12 | 12 | 12 |
| #4 | 12 | 12 | 12 | 12 | 12 | 12 |
| #5 | 12 | 14 | 12 | 14 | 12 | 14 |
| #6 | 13 | 19 | 12 | 17 | 12 | 17 |
| #7 | 18 | 25 | 16 | 22 | 14 | 20 |
| #8 | 23 | 33 | 20 | 28 | 18 | 25 |
| #9 | 30 | 41 | 26 | 36 | 23 | 32 |
| #10 | 38 | 52 | 33 | 45 | 29 | 41 |
| #11 | 46 | 64 | 40 | 56 | 36 | 50 |
| #14 | 63 | 87 | 54 | 76 | 49 | 68 |
| #18 | 81 | 113 | 70 | 98 | 63 | 88 |
| Bar | = 3 ksi | = 4 ksi | = 5 ksi | |||
|---|---|---|---|---|---|---|
| Top bar | Top bar | Top bar | ||||
| #3 | 12 | 12 | 12 | 12 | 12 | 12 |
| #4 | 12 | 12 | 12 | 12 | 12 | 12 |
| #5 | 12 | 12 | 12 | 12 | 12 | 12 |
| #6 | 12 | 15 | 12 | 14 | 12 | 14 |
| #7 | 15 | 20 | 13 | 18 | 12 | 16 |
| #8 | 19 | 26 | 16 | 23 | 15 | 20 |
| #9 | 24 | 33 | 21 | 29 | 19 | 26 |
| #10 | 30 | 42 | 26 | 36 | 23 | 33 |
| #11 | 37 | 52 | 32 | 45 | 29 | 40 |
| #14 | 50 | 70 | 44 | 61 | 39 | 54 |
| #18 | 65 | 90 | 56 | 78 | 50 | 70 |
751.40.8.4.2.7 Minimum lap length for uncoated Grade 40 tension lap splices, Llap (AASHTO 8.32)
| Other than Top Bars | Top Bars | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| = 3 ksi | = 4 ksi | = 5 ksi | = 3 ksi | = 4 ksi | = 5 ksi | |||||||||||||
| Bar | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C |
| #3 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 16 | 21 | 12 | 16 | 21 | 12 | 16 | 21 |
| #4 | 12 | 12 | 14 | 12 | 12 | 14 | 12 | 12 | 14 | 12 | 16 | 21 | 12 | 16 | 21 | 12 | 16 | 21 |
| #5 | 12 | 13 | 17 | 12 | 13 | 17 | 12 | 13 | 17 | 14 | 19 | 24 | 14 | 19 | 24 | 14 | 19 | 24 |
| #6 | 13 | 17 | 22 | 12 | 16 | 21 | 12 | 16 | 21 | 19 | 24 | 31 | 17 | 22 | 29 | 17 | 22 | 29 |
| #7 | 18 | 23 | 30 | 16 | 20 | 26 | 14 | 19 | 24 | 25 | 32 | 42 | 22 | 28 | 37 | 20 | 26 | 34 |
| #8 | 23 | 30 | 40 | 20 | 26 | 34 | 18 | 24 | 31 | 33 | 42 | 55 | 28 | 37 | 48 | 25 | 33 | 43 |
| #9 | 30 | 38 | 50 | 26 | 33 | 43 | 23 | 30 | 39 | 41 | 54 | 70 | 36 | 47 | 61 | 32 | 42 | 54 |
| #10 | 38 | 49 | 63 | 33 | 42 | 55 | 29 | 38 | 49 | 52 | 68 | 89 | 45 | 59 | 77 | 41 | 53 | 69 |
| #11 | 46 | 60 | 78 | 40 | 52 | 68 | 36 | 46 | 61 | 64 | 84 | 109 | 56 | 72 | 95 | 50 | 65 | 85 |
| Other than Top Bars | Top Bars | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| = 3 ksi | = 4 ksi | = 5 ksi | = 3 ksi | = 4 ksi | = 5 ksi | |||||||||||||
| Bar | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C |
| #3 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 16 | 21 | 12 | 16 | 21 | 12 | 16 | 21 |
| #4 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 16 | 21 | 12 | 16 | 21 | 12 | 16 | 21 |
| #5 | 12 | 12 | 14 | 12 | 12 | 14 | 12 | 12 | 14 | 12 | 16 | 21 | 12 | 16 | 21 | 12 | 16 | 21 |
| #6 | 12 | 14 | 18 | 12 | 13 | 17 | 12 | 13 | 17 | 15 | 19 | 25 | 14 | 18 | 23 | 14 | 18 | 23 |
| #7 | 15 | 19 | 24 | 13 | 16 | 21 | 12 | 15 | 20 | 20 | 26 | 34 | 18 | 23 | 29 | 16 | 21 | 27 |
| #8 | 19 | 24 | 32 | 16 | 21 | 28 | 15 | 19 | 25 | 26 | 34 | 44 | 23 | 29 | 38 | 20 | 26 | 34 |
| #9 | 24 | 31 | 40 | 21 | 27 | 35 | 19 | 24 | 31 | 33 | 43 | 56 | 29 | 37 | 49 | 26 | 33 | 44 |
| #10 | 30 | 39 | 51 | 26 | 34 | 44 | 23 | 30 | 39 | 42 | 54 | 71 | 36 | 47 | 62 | 33 | 42 | 55 |
| #11 | 37 | 48 | 63 | 32 | 42 | 54 | 29 | 37 | 49 | 52 | 67 | 87 | 45 | 58 | 76 | 40 | 52 | 68 |
751.40.8.4.3 Miscellaneous
Negative Moment Steel over Intermediate Supports
Dimension negative moment steel over intermediate supports as shown.
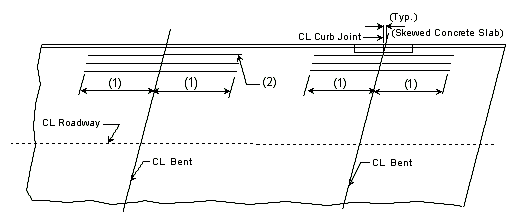
| Prestressed Structures: | |
|---|---|
| (1) | Bar length by design. |
| (2) | Reinforcement placed between longitudinal temperature reinforcing in top. |
Bar size: #5 bars at 7-1/2" cts. (Min.) #8 bars at 5" cts. (Max.)
| Steel Structures: | |
|---|---|
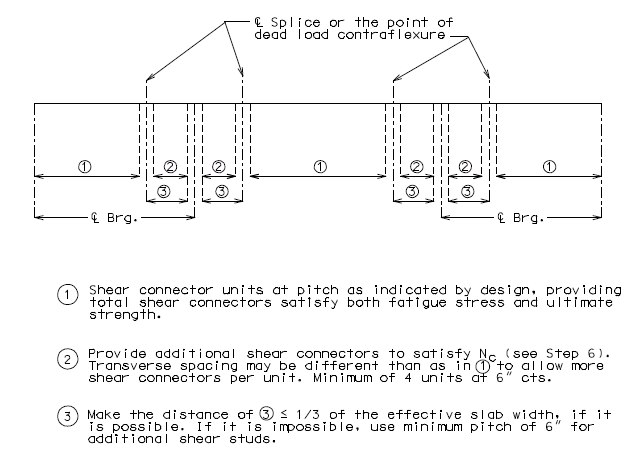
| (1) | Extend into positive moment region beyond "Anchor" Stud shear connectors at least 40 x bar diameter x 1.5 (Epoxy Coated Factor)(*) as shown below. (AASHTO 10.38.4.4 & AASHTO 8.25.2.3) |
| (2) | Use #6 bars at 5" cts. between longitudinal temperature reinforcing in top. |
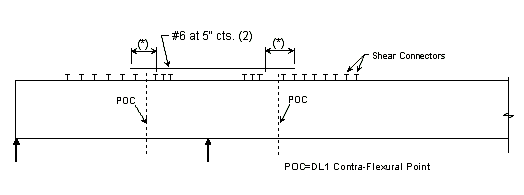
| (*) | 40 x bar diameter x 1.5 = 40 x 0.75" x 1.5 = 45” for #6 epoxy coated bar. |
751.40.8.5 General Superstructure
751.40.8.5.1 Concrete Slabs
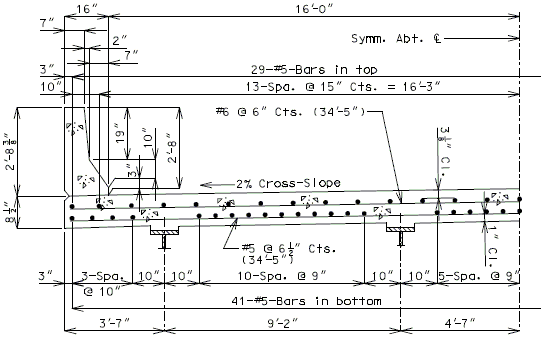
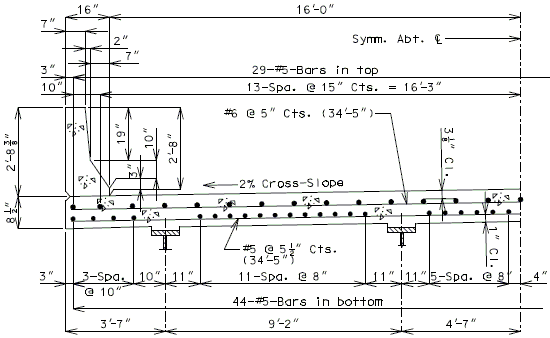
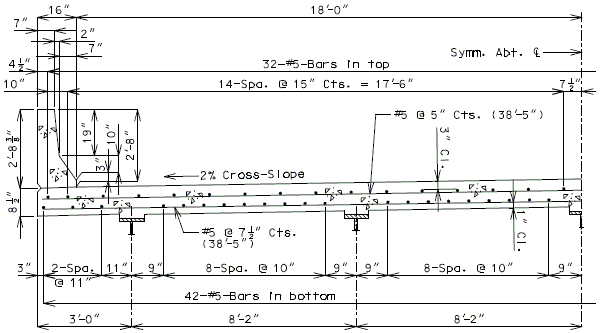
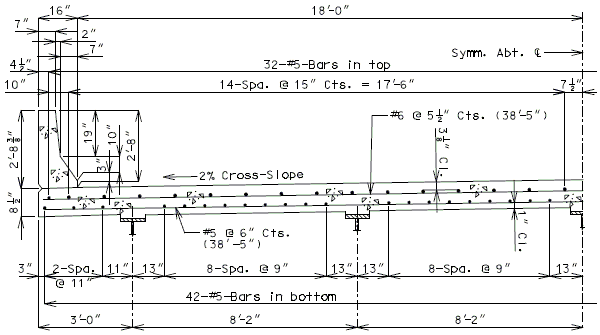
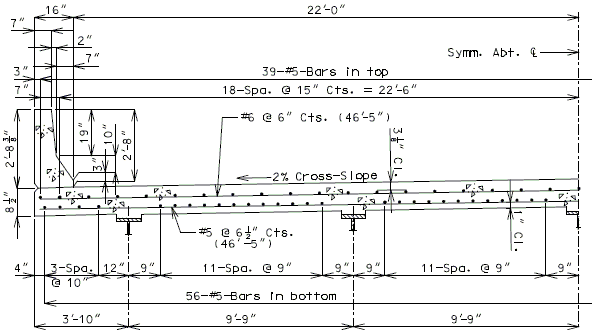
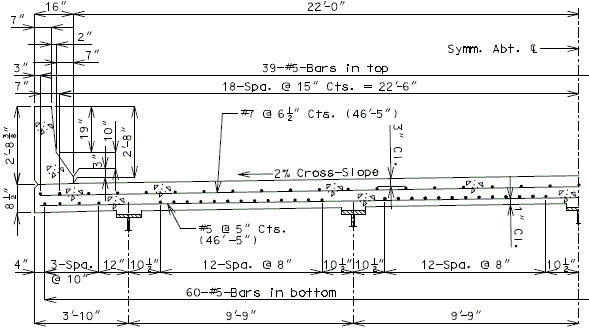
751.40.8.5.1.1 Design Criteria
Slabs on Girders
Stresses:
= 1,600 psi = 4,000 psi = 8 = 60,000 psi
Moments Over Interior Support (Use for positive moment reinf. also) (Sec. 1.5 E40A)
| Dead Load = | (Continuous over 5 supports) | |
| Dead Load = | (Continuous over 4 supports) |
| Live Load = | Continuity Factor | = 0.8 | ||
| Impact Factor | = 1.3 | |||
| P | = 16 Kips for HS20 | |||
| P | = 20 Kips for HS20 Modified | |||
| Design Load: | ||||
Cantilever Moment
Dead Load = Moment due to slab, F.W.S. and S.B.C.
Live Load:
Wheel Load =
Where:
| = Wheel load (apply impact factor) | |
| = Distance from load to support (ft.) | |
| = |
Collision Load =
Where:
| = 10 kips (Collision force) | |
| = Moment arm (Curb ht.+ 1/2 Slab th.) | |
| = |
Where:
| = Distance from center of gravity of barrier to support |
Design of top reinforcement is based on maximum moment over supports or cantilever moment. Flexural reinforcement shall meet the criteria of AASHTO Art. 8.16.3.
When designing for bottom transverse reinforcement, a 1" wearing surface is removed from the effective depth.
Prestressed panels replace the bottom transverse reinforcement.
Prestressed panels are assumed to carry DL1 stresses. Therefore, the negative moment due to DL1 at interior supports may be neglected.
The maximum P/S panel width (clear span + 6") for HS20 Modified is 9'-6". (Based on 10'-0" girder spacing and 10" flanges) The maximum P/S panel width (clear span + 6") for HS20 is 9'-11".
Distribution of Flexural Reinforcement
Allowable Stress:
Where:
| = 130 k/in. | |
| = Dist. from extreme tension fiber to center of closest bar (concrete cover shalll not be taken greater than 2") | |
| = Effective tension area of concrete | |
| = | |
| = Bar spacing ctr. to ctr. |
Actual Stress:
Where:
| = Service load moment | |
| = Area of steel | |
| = | |
| = | |
| = | |
| = | |
| = Effective width | |
| = Effective depth |
Distribution of flexural reinforcement does not need to be checked in concrete considered unexposed to weather.
Longitudinal distribution reinforcement:
Top of slab - use #5 bars at 15" cts. for temperature distribution.
Bottom of slab - by design.
Negative moment reinforcement over supports:
Steel structures - add. #6 bars at 5" between #5 bars.
P/S girder structures - by design.
Additional reinforcement over supports shall be a minimum of #5 bars and a maximum of #8 bars at 5" ctrs. When necessary, replace the #5 temperature reinforcement with a larger bar to satisfy negative moment reinforcement requirement, but keep all bars within two bar sizes.
Note: See details of negative moment reinforcement.
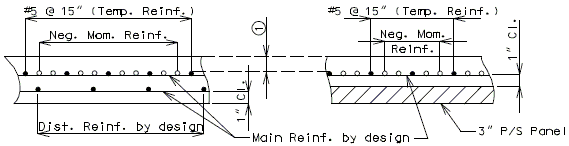
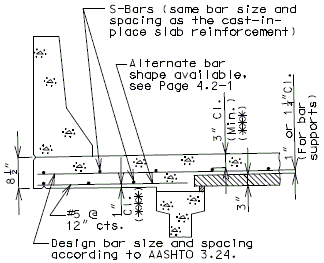
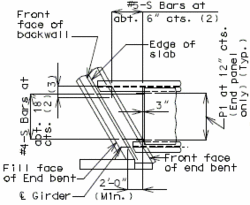
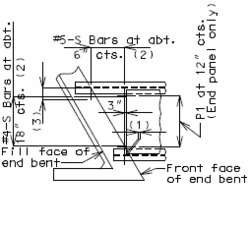
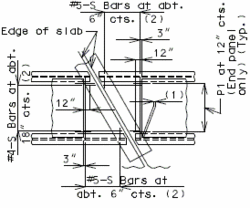
| |
| CIP Slab | P\S Panel Slab |
|---|---|
| 3" Cl. preferred min., 2 3/4" Cl. preferred min. for P/S panels to accommodate #8 bars over supports and 2 1/2" Cl. absolute min. by AASHTO 8.22.1. |
Method of measurement:
The area of the concrete slab shall be measured and computed to the nearest square yard. This area shall be measured transversely from out to out of slab and longitudinally from end to end of bridge slab.
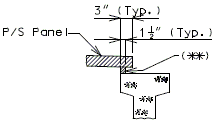
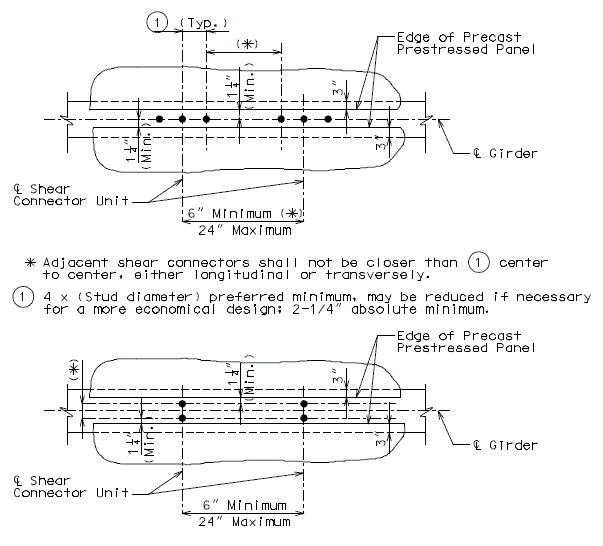
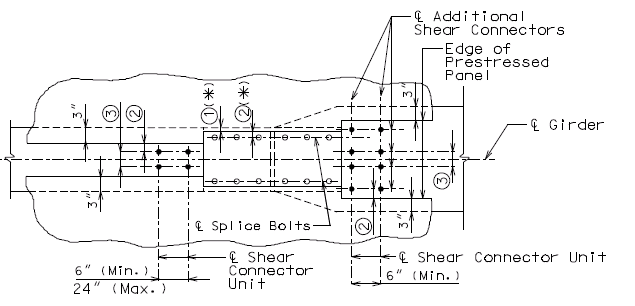
Precast Prestressed Panels
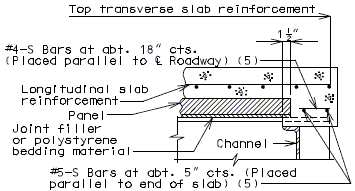
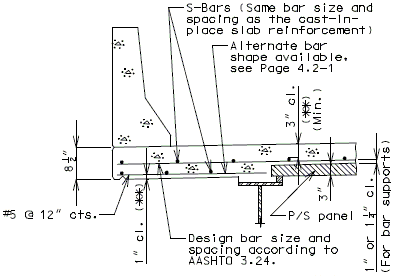
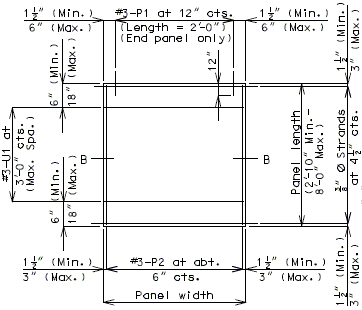
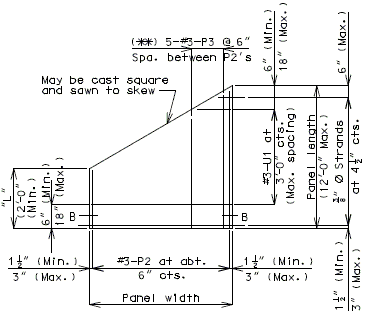
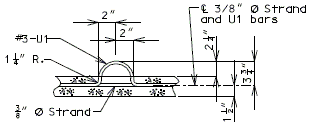
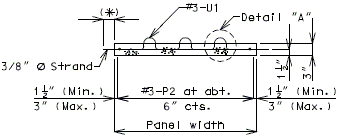
3" Precast prestressed concrete panels with 5-1/2" minimum cast-in-place concrete will be the standard slab used on all girder superstructures except curved steel structures.
Concrete for prestressed panels shall be Class A1 with = 6,000 psi, = 3,500 psi. Prestressing tendons shall be uncoated, low-relaxation, seven-wire(7) strands for prestressed concrete conforming to AASHTO M203 Grade 270, with nominal diameter of strand = 3/8" and area = 0.085 sq.in., minimum ultimate strength = 22.95 kips (270 ksi), and strand spacing = 4.5 inches.
Panels shall be set on joint filler or polystyrene bedding material. Filler thickness shall be a Min. of 3/4" and a Max. of 2". Standard filler width is 1 1/2" except at splice plates where 3/4" Min. is allowed to clear splice bolts. Joint filler thickness may be reduced to a minimum of 1/4" over splice plates on steel structures. For prestressed girder structures, joint filler thickness may be varied within these limits to offset girder camber or at the contractor's option a uniform 3/4" (Min.) thickness may be used throughout. The same thickness shall be used under any one edge of any panel and the maximum change in thickness between adjacent panels shall be 1/4 inch for steel spans and 1/2 inch for concrete spans.
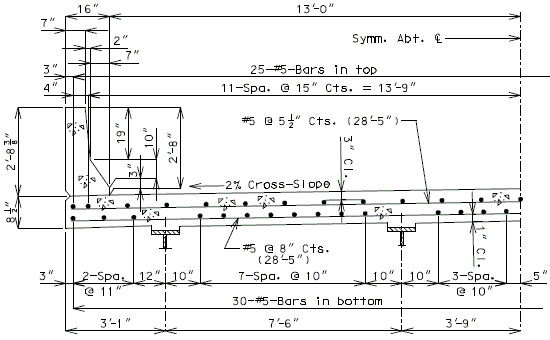
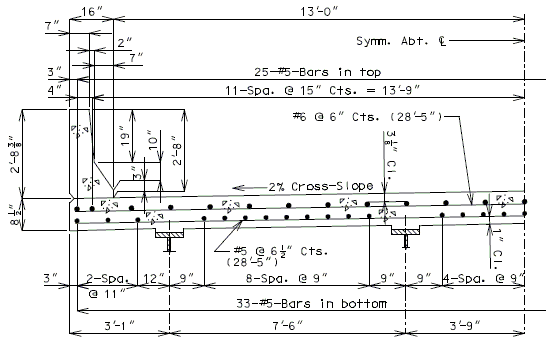
Standard roadway cross sections and slab reinforcement for HS20 and HS20 Modified live loads are shown in this section. Reinforcement shown is for a cast-in-place slab or a P/S panel slab with the bottom layer of reinforcement between girders being replaced by the panels. Cantilever reinforcement details for P/S panel slab are shown in this section.
- Maximum panel width (clear span + 6") = 9'-6" for HS20 Modified.
- Maximum panel width (clear span + 6") = 9'-11" for HS20.
When a barrier or railing is permanently required on the structure, other than at the edge of slab, precast prestressed panels will not be allowed in the bay underneath the barrier or railing. Prestressed panels are not allowed for use as simply supported for live loads, i.e. staging, where only two supports may be provided for live loads.
S.I.P.
Stay-in-place corrugated metal forms with cast-in-place concrete may be used on horizontally curved steel structures with the approval of the Structural Project Manager.
The standard slab reinforcements shown in this section for HS20 live load were designed using S.I.P. Dead Loads. If design is for HS20 Modified, the standard slab reinforcement needs to be checked for S.I.P. forms.
The bottom transverse reinforcement shall maintain a 1" clear distance from the top of forms.
C.I.P.
8 1/2" cast-in-place concrete slab with conventional forming may be used at the contractor's option, on all girder structures. Conventional forming shall also be used between girders with stage construction joints.
|
| |
| Panels-Squared Ends | Panels-Skewed Ends | |
|---|---|---|
| PLAN OF PRECAST PRESTRESSED PANELS PLACEMENT | ||
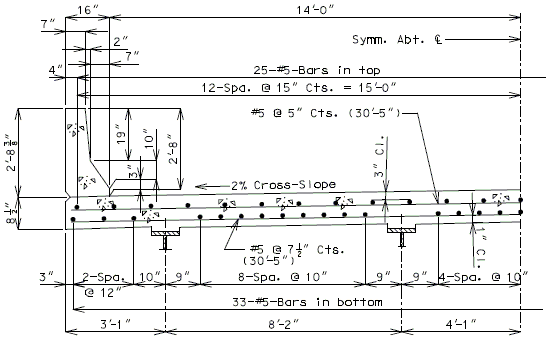
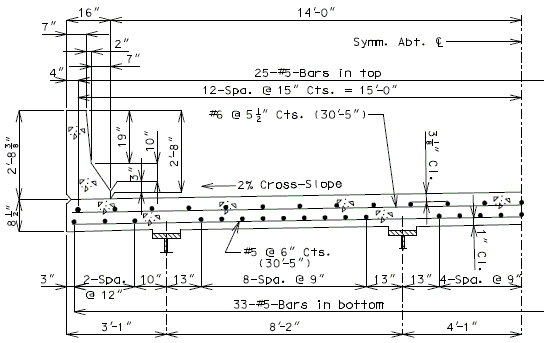
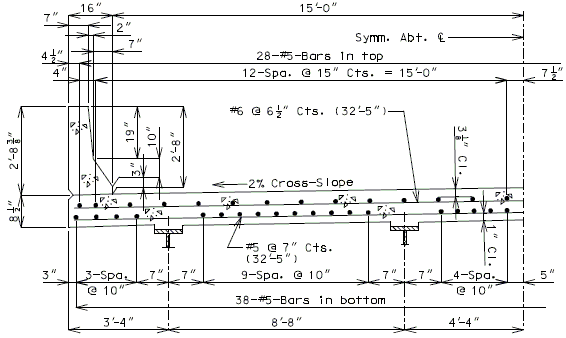
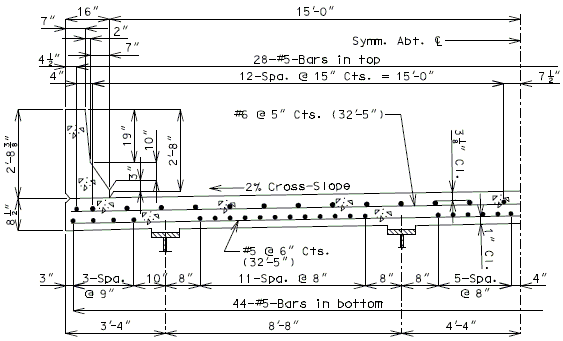
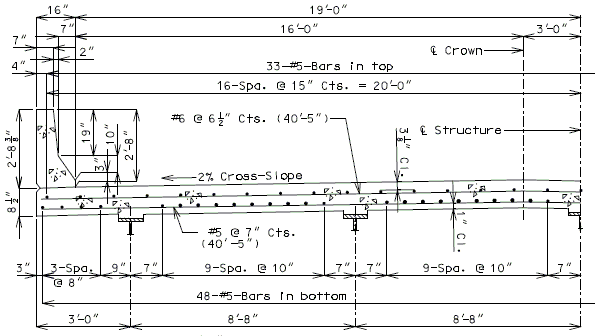
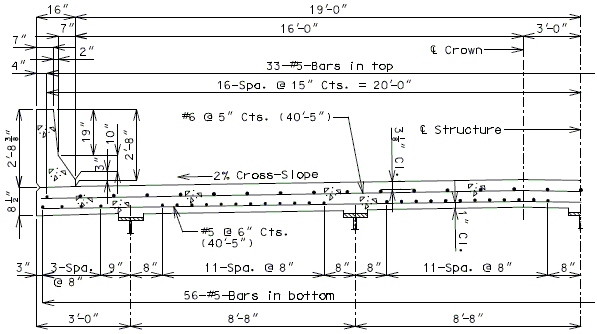
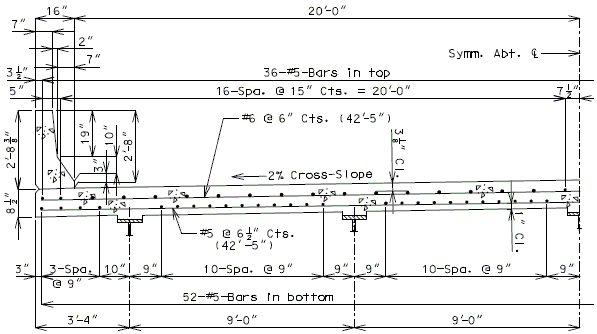
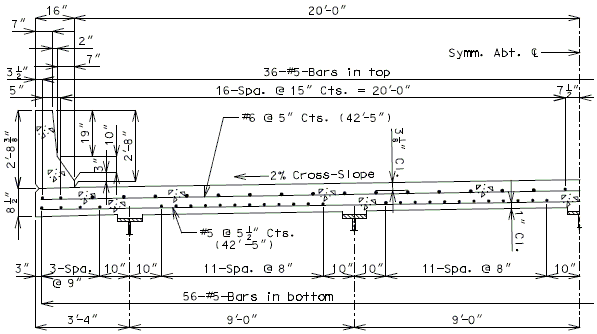
751.40.8.5.1.2 Details of Concrete Slabs for Structures
751.40.8.5.2 Timber Floor
| Maximum stringer spacing as determined by strength of timber floor | ||
|---|---|---|
| Stress = 1,200 lbs. per square inch | ||
| H-10 | H-15 | |
| (*) 3" x 12" Plank | 18" + 1/2 Flange Width | 16" + 1/2 Flange Width |
| 4" Laminated Floor | 2'-11" + 1/2 Flange Width | 2'-3" + 1/2 Flange Width |
| 6" Laminated Floor | 6'-0" + 1/2 Flange Width | 4'-4" + 1/2 Flange Width |
| Stress = 1,600 lbs. per square inch | ||
| H-10 | H-15 | |
| 3" x 12" Plank | 23" + 1/2 Flange Width | 21" + 1/2 Flange Width |
| 4" Laminated Floor | 3'-9" + 1/2 Flange Width | 2'-11 1/2" + 1/2 Flange Width |
| 6" Laminated Floor | 7'-10 3/4" + 1/2 Flange Width | 5'-9" + 1/2 Flange Width |
751.40.8.5.3 Steel Grid Bridge Flooring
In general, the 5" depth (concrete filled to half depth) steel grid bridge flooring shall be specified. Bar spacing may vary as necessary to meet minimum section modulus requirements. Main member spacing shall not exceed 10" and cross bar spacing shall not exceed 4". At present, the manufacturers of the following types have provided data to show they are acceptable:
- Greulich 5" Standard
- Foster 5" Standard
The section properties and maximum span for HS20 loading have been computed for these types and are as follows:
| Company | (For Design Purpose only) Weight (PSF) (Steel & Conc.) |
Main bar Spacing |
Cross bar Spacing |
Moment of Inertia | ||
| Mid Span | Over-Support | |||||
| Conc. | Steel | Steel | ||||
| Greulich | 48.0 | 7 1/2" | 3 3/4" | 99.41 | 12.43 | 9.03 |
| Foster | 48.0 | 8" | 4" | 128.1 | 16.01 | 12.25 |
| Company | Section Modulus | Maximum Span (*) | ||||||
| Mid-Span | Over-Support | Simple Span | Continuous Spans | |||||
| Conc. (Top) |
Steel (Bott.) |
Steel (Top) |
Steel (Bott.) |
ASTM A709 Gr. 36 |
ASTM A709 Gr. 50W |
ASTM A709 Gr. 36 |
ASTM A709 Gr. 50W | |
| Greulich | 59.5 | 3.53 | 3.90 | 3.14 | 4'-4" | 5'-10" | 5'-10" | 7'-1" |
| Foster | 72.5 | 4.68 | 5.25 | 4.30 | 5'-9" | 7'-5" | 7'-2" | 9'-4" |
The cross-section DETAILS used in computing the section properties are shown on the sketches on the following sheets. Maximum span determination included an allowance for a 35#/sq.ft. future
wearing surface and assumed a wheel load to be distributed, normal to the main bars, over a width of 4'-0".
(Place the following note on the Bridge Plans with the Steel Grid Details.
Note: The steel grid deck shall be electrically grounded.
(*) For main beams of grid either parallel or perpendicular to traffic.
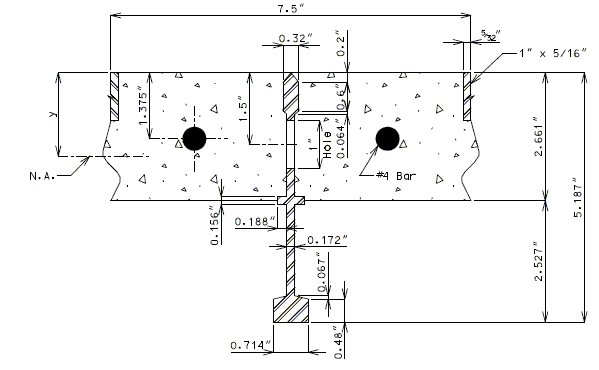
| Composite Section | Steel Section Only (net) | |
| y | 1.671" | 2.317" |
| Note: | Dimensions obtained form Greulich plans. |
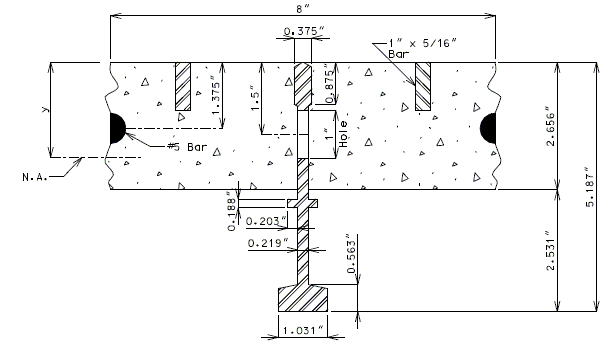
| Composite Section | Steel Section Only (net) | |
| y | 1.766" | 2.338" |
| Note: | Dimensions obtained form Foster Catalog. |
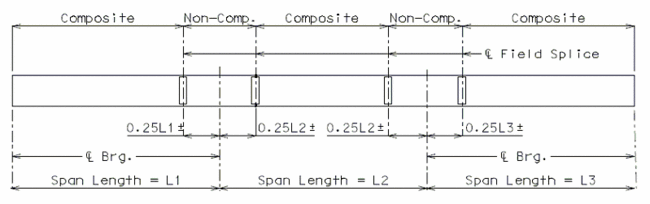
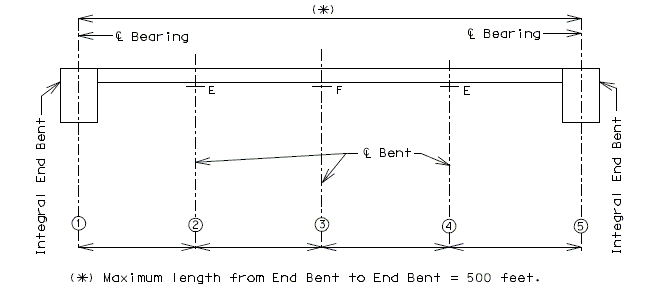
751.40.8.5.4 Longitudinal Diagrams
751.40.8.5.4.1 Hinged Beam Connections
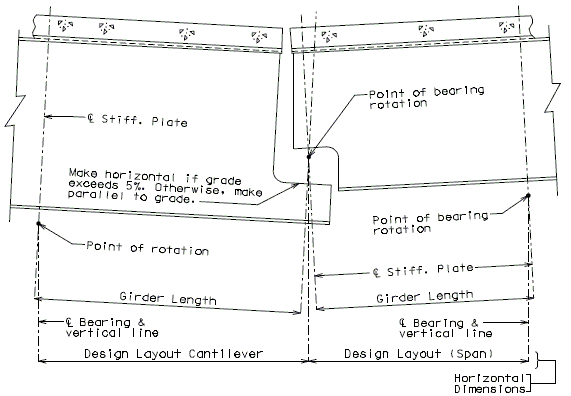
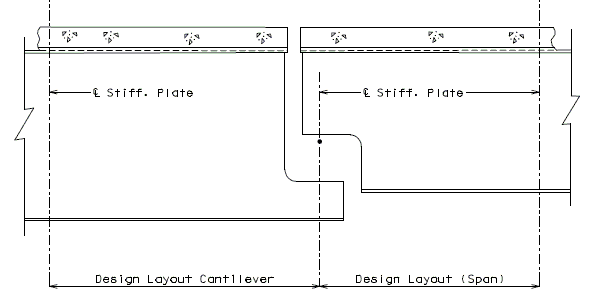
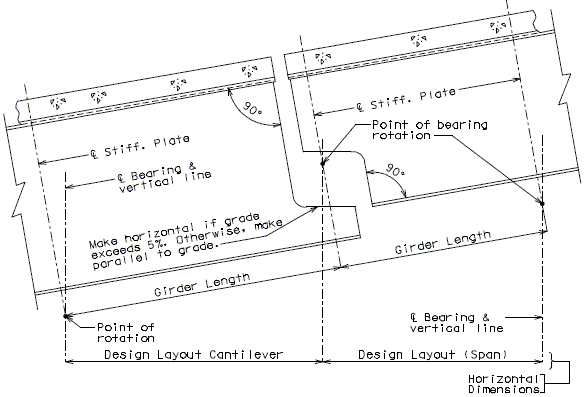
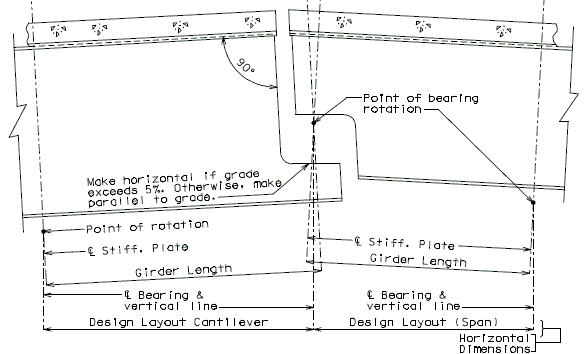
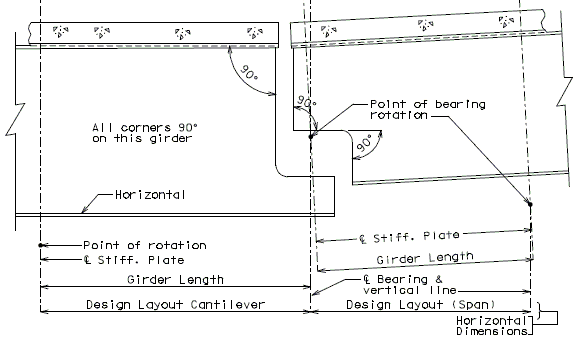
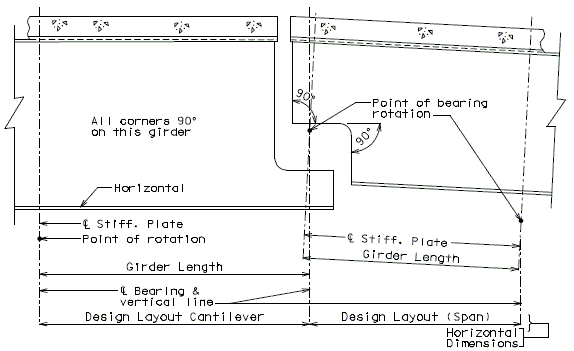
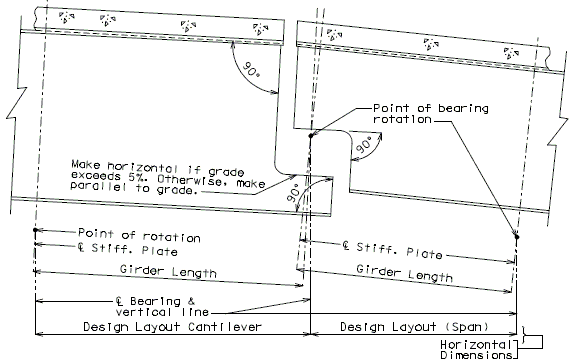
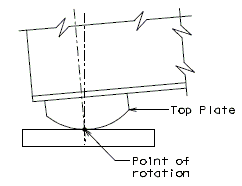
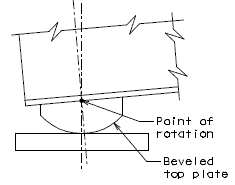
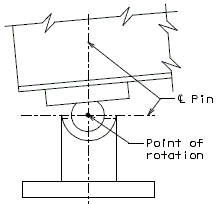
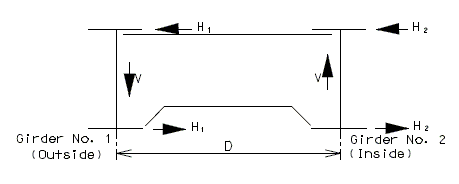
The diagrams of various joints in steel structures are intended to be guides primarily for the determination of horizontal longitudinal dimensions for the plan view on the first sheet of plans.
These diagrams are not to be detailed on the design plans. However, the arrangement of the joints should be useful in detailing the longitudinal diagram for structural steel, particularly for bridges on grades and vertical curves.
Longitudinal dimensions for the plan of structural steel and for the plan of slab shall be horizontal from centerline bearing to centerline bearing.
For proper correlation of details when developing plans for widening or redecking bridges, match the method of dimensioning on the new plans with the method used on the originals.
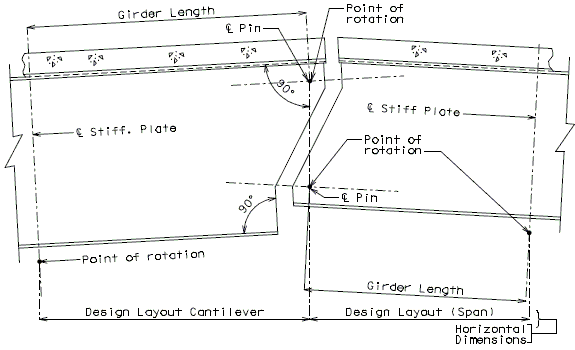
|
| Geometrics for Hanger Beam Connections for Bridges on Crown Vertical Curves |
|---|
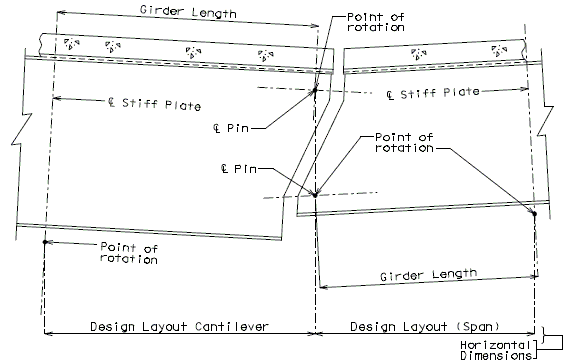
|
| Geometrics for Hanger Beam Connections for Bridges on Sag Vertical Curves |
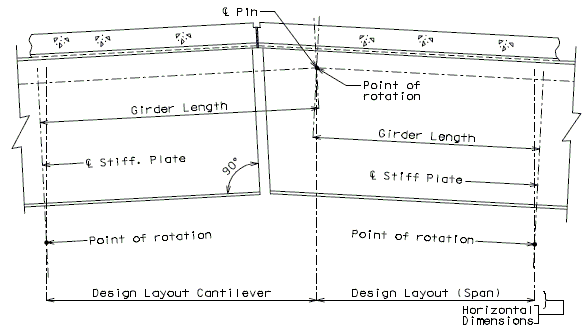
|
| Geometrics for Pin Plate Connections for Bridges on Crown Vertical Curves |
|---|
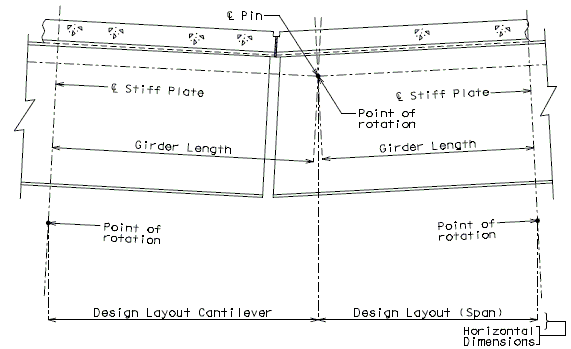
|
| Geometrics for Pin Plate Connections for Bridges on Sag Vertical Curves |
751.40.8.5.4.2 Longitudinal Sections
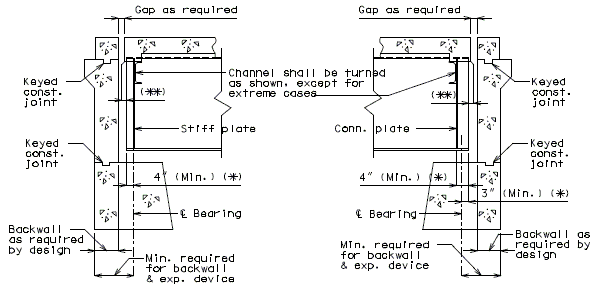
| |
| Bearing Stiffener | Connection Plate |
|---|---|
| Structures Not on Grade (Typical) | |
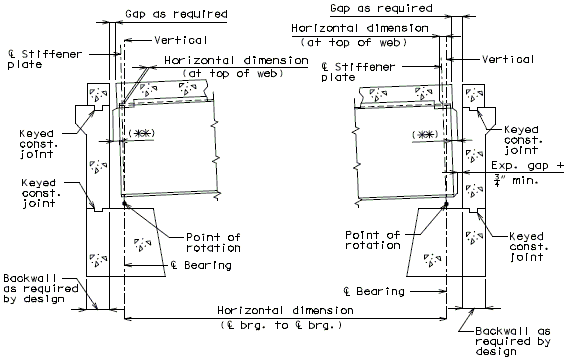
| |
| Structures on Grade (Typical) | |
| (*) | Parallel to Girder. All other dimensions shown are normal to backwall. |
| (**) | See EPG 751.13 Expansion Devices for dimension of overhang from end of stringer or girder to face of plate, edge of concrete or face of vertical leg of angle. |
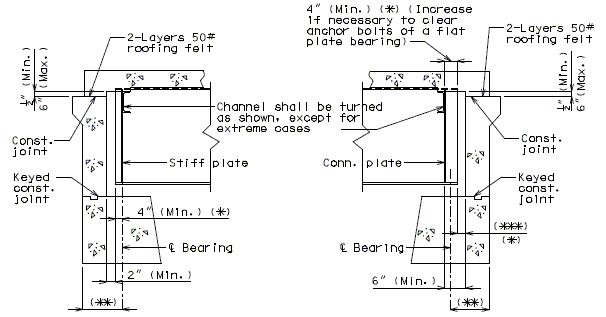
| |
| Bearing Stiffener | Connection Plate |
|---|---|
| Structures Not on Grade (Typical) | |
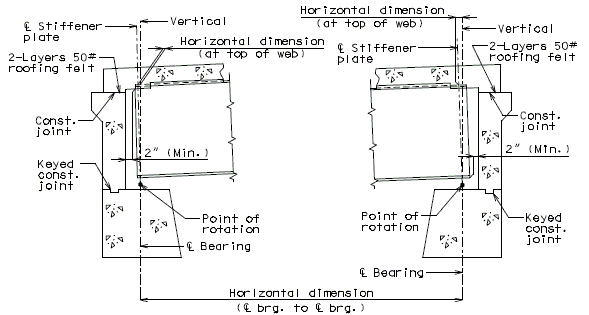
| |
| Structures on Grade (Typical) | |
| (*) | Parallel to Girder. All other dimensions shown are normal to backwall. |
| (**) | 18" min. (Use same dimension as the expansion device end on 3-span continuous, if it is not more than 2" greater.) |
| (***) | 3" min. for type C, D and E bearing, and 2" min. for an elastomeric bearing. |
|
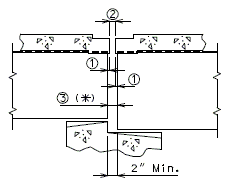
|
| No Expansion Device | Expansion Device |
|---|
|
|
| Structures Not on Grade (Typical) | |
|---|---|
| |
| Structures On Grade (Typical) | |
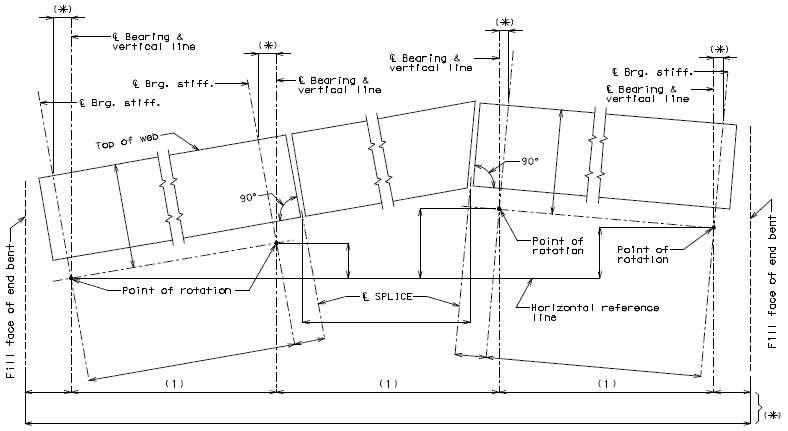
|
| Elevation of Longitudinal Steel Diagram |
|---|
| Note: | The typical elevation shown above should be detailed on the plans for all steel structures that are on vertical curve grades. |
| (1) | Longitudinal dimensions are horizontal from centerline Brg. to centerline Brg. |
| (*) | Horizontal dimensions. |
| BLOCKING DIAGRAM SHOULD NOT BE USED FOR CAMBERED GIRDERS. | |
|---|---|
751.40.8.5.5 Miscellaneous Bearing Connections
751.40.8.5.5.1 Typical Details of “Hinged Connection"
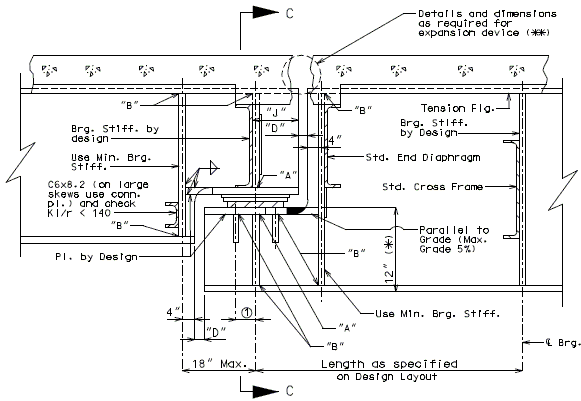
| ||||||||||||||||
| Section Showing Hinged Beam Connection | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
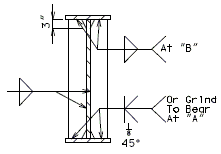
| ||||||||||||||
| Plan of Brg. Plate | ||||||||||||||||
| Detail of Web at Radius Transition |
Typical Welding Details for Stiff. Plates | |||||||||||||||
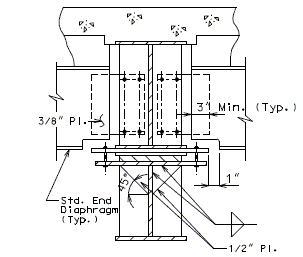
|
| |||||||||||||||
| Section C-C | ||||||||||||||||
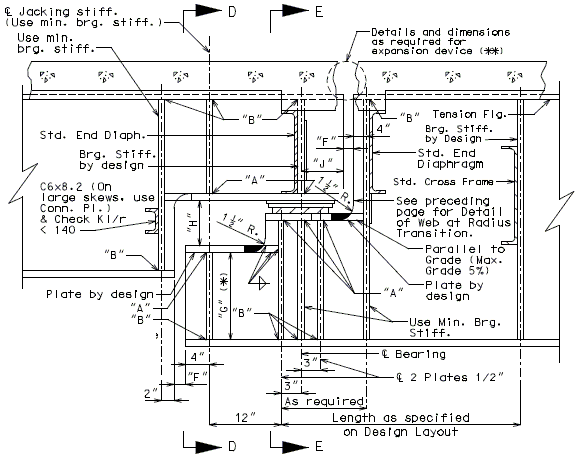
| |||
| Section Showing Hinged Beam Connection | |||
|---|---|---|---|
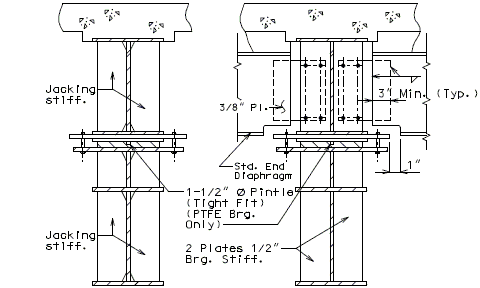
| |||
| Section D-D | Section E-E | ||
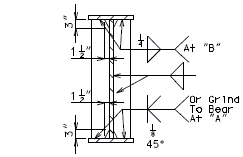
| |||
| Typical Welding Details for Stiff. Plates | |||
| (*) | See below for dimension "G". |
| (**) | See EPG 751.13 Expansion Devices |
| "F" | = Gap as required for expansion (3" Min.). |
| "H" | = 10 3/4" Min. (12" preferred.) |
| "J" | = 5" for bearing with 3" web thickness. Use 6" for all others. |
| All dimensions shown are minimum, increase, as necessary. | |
| Web Thickness |
Depth "G" |
(*) Allowable Dead Load Reactions, Kips (At 150% Overstress) |
Web Thickness |
Depth "G" |
(*) Allowable Dead Load Reactions, Kips (At 150% Overstress) | |
|---|---|---|---|---|---|---|
| 5/16" | 8" | 45.0 | 7/16" | 8" | 63.0 | |
| 5/16" | 9" | 50.6 | 7/16" | 9" | 70.8 | |
| 5/16" | 10" | 56.2 | 7/16" | 10" | 78.7 | |
| 5/16" | 11" | 61.8 | 7/16" | 11" | 86.6 | |
| 5/16" | 12" | 67.5 | 7/16" | 12" | 94.5 | |
| 5/16" | 13" | 73.1 | 7/16" | 13" | 102.3 | |
| 5/16" | 14" | 78.8 | 7/16" | 14" | 110.2 | |
| 5/16" | 15" | 84.3 | 7/16" | 15" | 118.1 |
| 3/8" | 8" | 54.0 | 1/2" | 8" | 72.0 | |
| 3/8" | 9" | 60.7 | 1/2" | 9" | 81.0 | |
| 3/8" | 10" | 67.5 | 1/2" | 10" | 90.0 | |
| 3/8" | 11" | 74.2 | 1/2" | 11" | 99.0 | |
| 3/8" | 12" | 81.0 | 1/2" | 12" | 108.0 | |
| 3/8" | 13" | 87.7 | 1/2" | 13" | 117.0 | |
| 3/8" | 14" | 94.5 | 1/2" | 14" | 126.0 | |
| 3/8" | 15" | 101.2 | 1/2" | 15" | 135.0 |
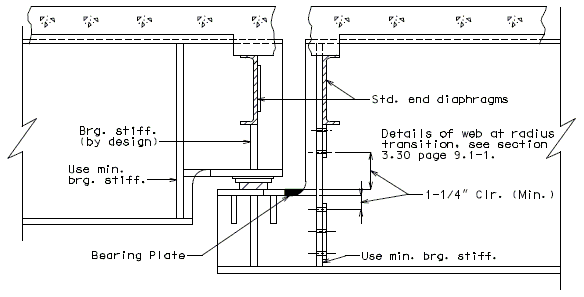
|
| Section Showing Hinged Beam Connection |
|---|
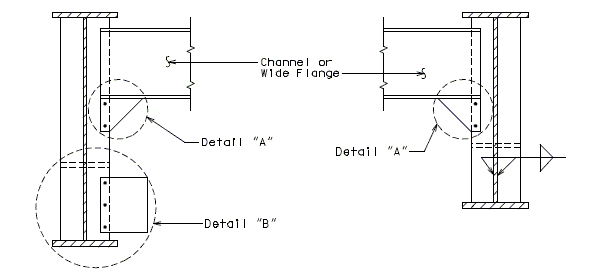
| |
| Plate Girder 42" Thru 46" Also 48" and Over |
Plate Girder 36" Thru 40" |
|---|---|
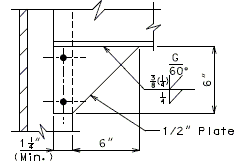
|
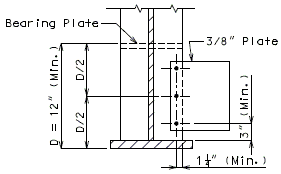
|
| Detail "A" | Detail "B" |
|---|
| Note: | Modify standard end diaphragm connections as shown above, if clearance problems exist between bearing plate and end diaphragm connection bolts. |
751.40.8.6 Composite Design
751.40.8.6.1 General
GENERAL
This portion of the article pertains to structures composed of steel girders with concrete slab connected by shear connectors. The stresses of composite girders and slab shall be computed based on the composite cross-section properties and shall be consistent with the properties of the various materials used. The regions subjected to positive moment are considered as composite and the regions subjected to negative moment are considered as non-composite. For the initial girder design, composite/non-composite regions can be approximately assumed as:
SECTION PROPERTIES
Cross-section properties of the composite section shall include concrete slab and steel section.
Cross-section properties of the non-composite section shall include steel section only.
Use composite property for positive moment section.
Use non-composite property for negative moment section. The effect of reinforcing steel in the section is not considered.
The ratio of modulus of elasticity of steel to that of concrete, n, shall be assumed to be eight. The effect of creep shall be considered in the design of composite girders which have dead loads acting on the composite section. In such structures, n=24 shall be used.
DESIGN UNIT STRESSES (also see note A1.1 in EPG 751.50 Standard Detailing Notes)
Reinforcement Concrete
| Reinforcing Steel (Grade 60) | = 24,000 psi | = 60,000 psi |
| Class B-2 Concrete (Substructure) | = 1,600 psi | = 4,000 psi |
Structural Steel
| Structural Carbon Steel (ASTM A709 Grade 36) | = 20,000 psi | = 36,000 psi |
| Structural Steel (ASTM A709 Grade 50) | = 27,000 psi | = 50,000 psi |
| Structural Steel (ASTM A709 Grade 50W) | = 27,000 psi | = 50,000 psi |
751.40.8.6.2 Design
751.40.8.6.2.1 Shear Connector Design
The shear connectors shall be designed for fatigue and checked for ultimate strength (AASHTO Article 10.38.5.1).
Step 1:
Compute Vr, the range of shear in kips, from the structural analysis, due to live loads and impact, for entire span.
At any section, the range of shear shall be taken as the difference in the minimum and maximum shear envelopes (excluding dead loads).
Step 2:
Use the average Vr per span, for the section of the span that is assumed to act compositely (from end of span to point of contraflexure for end spans, or from point of contraflexure to point of contraflexure for int. spans).
Step 3:
Using the average Vr from step 2, compute the range of horizontal shear load per linear inch, Sr in kips per inch, at the junction of the slab and stringer from the following equation:
(AASHTO Article 10.38.5.1.1 Eq. 10-58)
where:
= static moment of the transformed compressive concrete area about the neutral axis of the composite section, in cubic inches (*);
= moment of inertia of the transformed composite girder in positive moment regions in inches to the fourth power (*).
(*) In the formula, the compressive concrete area is transformed into an equivalent area of steel by dividing the effective concrete flange width by the modular ratio n=8.
Step 4:
Compute the allowable range of horizontal shear, Zr, in pounds on an individual connector, welded stud, by use of the following formula:
where:
=height of stud in inches;
=diameter of stud in inches;
=13,000 for 100,000 cycles
- 10,600 for 500,000 cycles
- 7,850 for 2,000,000 cycles
- 5,500 for over 2,000,000 cycles.
Step 5:
Compute the number of additional connectors required at point of contraflexure, N , from the following formula:
Pitch =
Where: Pitch = required pitch, in inches;
= the resistance of all connectors at one (1) transverse girder cross-section as a shear connector unit.
Note:
The pitch is to be constant and spaced in the composite section (round to the nearest inch).
Step 6:
Compute the required pitch of the shear connector units, pitch by the following formula:
(AASHTO Article 10.38.5.1.1 Eq. 10-69)
where:
= number of additional connectors required at the point of contraflexure;
= total area of longitudinal slab reinforcing steel for each girder over interior support;
= range of stress due to live load plus impact, in the slab reinforcement over the support (in lieu of more accurate computations, f may be taken as equal to 10,000 psi);
= the allowable range of horizontal shear on an individual connector.
This number of additional connectors, N , shall be placed adjacent to the point of dead load contraflexure within a distance equal to 1/3 of the effective slab width, if it is possible. If it is impossible, use minimum pitch of 6".
Step 7: Check connectors for ultimate strength
The number of connectors provided for fatigue must be checked to ensure that adequate connectors are provided for ultimate strength.
To check for ultimate strength, proceed as follows:
(1) Compute the force in the slab (P), which is defined as: at the point of maximum positive moment, the force in the slab is taken as the smaller value of the following two formulae:
(AASHTO Article 10.38.5.1.2 Eq. 10-62)
or
(AASHTO Article 10.38.5.1.2 Eq. 10-63)
Where:
= total area of the steel section including cover plates (if used);
= specified minimum yield point of the steel being used;
= compressive strength of concrete at age of 28 days;
= effective flange width given in AASHTO Article 10.38.3;
= thickness of concrete slab.
Note:
If it becomes impractical to place the number of shear connectors required by ultimate strength in the specified distance (structures with span ratios greater than 1.5); base the number and spacing of shear connectors on the fatigue analysis only.
Increase the haunch by 1/2"± more than what is required to make one size shear connector work for C.I.P. or S.I.P. option.
751.40.8.6.2.2 Shear Connector Spacing
If it becomes impractical to place the number of shear connectors required by ultimate strength in the specified distance (structures with span ratios greater than 1.5); base the number and spacing of shear connectors on the fatigue analysis only.
For a typical 3-spans bridge, the shear connector units can be approximately arranged as below:
751.40.8.6.3 Details
751.40.8.6.3.1 Shear Connector Details
Use precast prestressed panels on all tangent steel structures. Evaluate the viability of the use of P/S panels on curved structures on a case by case basis and use or include as an option to a CIP slab where deemed appropriate.
Whenever panels are used, the minimum top flange width shall be 12" for Plate Girders and 10" for Wide Flange Beams.
Steel girders shall be cambered when using P/S Panels. Minimum joint filler thickness is 3/4", except over splice plates, in which case use 1/4" minimum. Maximum joint filler thickness is 2".
Shear connectors shall have a minimum height equal to the top of panel.
Shear connectors shall be spaced by units and shear connectors in each unit shall be placed along of girder. On wide flange widths, two lines of connectors may be used if spacings and clearances allow.
Additional shear connectors, Nc, at point of contraflexure may be placed in units normal to girder as space allows or in a single row along girder as shown below:
P/S strands shall extend 3" minimum and 6" maximum past edge of precast prestressed panel and not closer than 1" to the adjacent panels.
Panel end at splices shall be notched to avoid bolt heads as shown below:
![]() 3/4" min. wide bearing edge for panel at splice, typ. (*)
3/4" min. wide bearing edge for panel at splice, typ. (*)
![]() 4 x (Stud diameter) preferred minimum, may be reduced if necessary for a more economical design; 2-1/4" absolute minimum.
4 x (Stud diameter) preferred minimum, may be reduced if necessary for a more economical design; 2-1/4" absolute minimum.
(*) In order to meet ![]() and
and ![]() above, it is necessary to have an edge bolt distance of 2" or greater for splice plate. For unusual cases, which would require field splices for flange widths 14" or 15" for P/S precast panel option, it will be necessary to change the top flange width to either 13" or 16" of equal area to maintain the 3/4" minimum panel bearing edge on the splice plates.
above, it is necessary to have an edge bolt distance of 2" or greater for splice plate. For unusual cases, which would require field splices for flange widths 14" or 15" for P/S precast panel option, it will be necessary to change the top flange width to either 13" or 16" of equal area to maintain the 3/4" minimum panel bearing edge on the splice plates.
Minimum joint filler thickness is 3/4" except over splice plates in which case use 1/4" minimum. When joint filler is less than 1/2" thick over splice plate, make the width of joint filler at splice the same width as panel on splice (maximum 1-1/2" wide).
Maximum difference in top of flange thickness should be checked so that joint filler thickness does not exceed 2".
751.40.8.6.3.2 Deflection
Allowable Live Load Deflection
| 1. | Composite Design: | Defl. | = 1/1000 of span; |
| 2. | Non-composite Design: | Defl. | = 1/800 of span |
- Where:
- Defl. = allowable deflection due to service live load plus impact.
Dead Load Deflection
Compute at 1/4 point for bridge with spans less than 75’, at 1/10 points for spans 75’ and over.
751.40.8.7 Wide Flange Beam Spans
751.40.8.7.1 Design
751.40.8.7.1.1 Design Data
Slabs
| Reinforcing Steel | = 60,000 psi | ||||
| Concrete | = 1,600 psi | = 4,000 psi | |||
| = 8 |
Simple Design Span
Design Span = Center to Center of Bearings.
Dead Load
Live Load Distribution Factors
See EPG 751.40.8.2.2 Distribution of Live Load
Live Load Deflection Allowable
| Composite | |
| Non-Composite |
Live Load Reaction
Live Load Wheel Line is the Live Load Reaction per Wheel Line, no distribution, no impact; Maximim Live Load Impact is the Live Load Reaction x Distribution Factor = Impact.
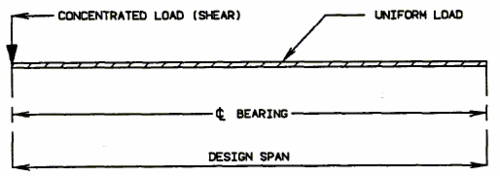
Typical Continuous Steel Structures - Integral End Bents:
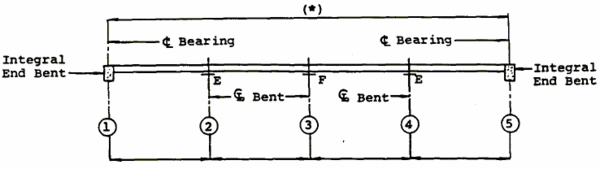
751.40.8.7.1.2 Stringer Design
Stresses:
| Steel: | AASHTO - Article 10.2, 10.32 | ||
| ASTM A709 Grade 36 | = 36,000 psi | ( = 20,000 psi) | |
| ASTM A709 Grade 50 & Grade 50W | = 50,000 psi | ( = 27,000 psi) | |
| Superstructure Concrete: | = 1,600 psi | |
| = 4,000 psi | ||
| = 8 |
| Reinforcing Steel: | = 60,000 psi |
Physical Properties of Spans
- Composite Design - See Widening and Repair - Composite Design.
- Non-Composite Design - Use "Constant I" analysis.
When the neutral axis of a composite section falls in the concrete fange, the section shall be designed as Non-Composite (21" Wide Flange is the smallest beam generaly made conposite).
Deflection
Live Load Deflection: AASHTO - Article 10.6 Composite - Allowable Deflection L/1000 Non-Composite - Allowable Deflection l/800 Dead Load Deflection: Compute at 1/4 points for bridges with spans less than 75', at 1/10 points for spans 75' and over. Give percentage of deflection due to weight of structural steel.
Fatigue Stress
AASHTO - Article 10.3 Case I, Case II or Case III (as specified on Bridge Memorandum generally within the following limitations).
Case I: Bridges with the TRUCK traffic count of 2500 or more vehicles per day (one direction). Case II: Bridges with traffic count of 750 or more vehicles per day, and less than 2500 TRUCK traffic count (one direction) per day. Case III: Bridges with traffic count of less than 750 vehicles per day, except when Live Loading is H20 or greater. No Fatigue: Bridges with traffic of less than 75 vehicles per day.
Economic Comparison
When comparing cost of low-alloy steels (A-572, Gr.-50, and A-588) to the cost of A-36 steel, the low-alloy steels shall be figured a t 3 1/2 cents for A-572, Gr.-50 and 5 1/4 cents for A-588 per pound more than A-36 steel. Cost comparisions will be based on current average bid prices that may be obtained from the CHIEF DESIGNER, for comparable bridges.
No overstressed will be permitted in the design.
Total Capacity of Exterior Griders (Dead Load and Live Load)
In no case shall an exterior stringer have less carrying capacity than an interior stringer.
751.40.8.7.1.3 Flange Plate Lengths
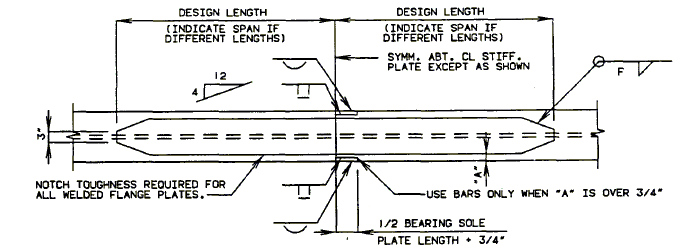
| |
| Top Flange | Bottom Flange |
|---|---|
| Details of Flange Plates at Intermediate Bents | |
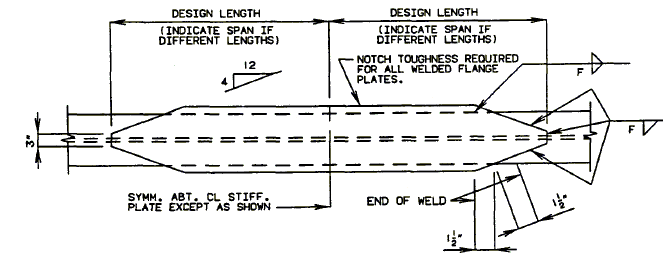
| |
| Details of Flange Plates at Intermediate Bents (Top and Bottom Flanges) | |
Allowable flange plate sizes are as shown with the section properties. Different plate sizes may be used on adjacent stringers.
Lengths to be shown on the bridge plans are those required as follows:
- Lengths each side of the bearing shall be the larger of:
- Theoretical End + Terminal Distance (***) or
- Point where the stress range (tension or reversal) in the beam flange is equal to or less than allowable fatigue stess range (Cat. E or E') or where the beam flange is in compression, whichever is smaller.
- Use Cat. E when the flange is less than or equal to 0.8 inch thick.
- Use Cat. E' when the flange is greater than 0.8 inch thick.
(***) Where the theoretical end = the point where the flange stress without cover plate less than or equal to base allowable stress. Terminal distance = 1 1/2 times nominal cover plate width.
The total length of the cover plate greater than or equal to (2D + 3'-0"). Where "D" = Depth of beam in feet.
When required lengths of plates vary by 12" or less on adjacent stringers or on each side of the centerline stiffener plate, use greater length for all such positions.
Plate lengths taken form the computer programs should be rouned up to at least the nearest 6".
751.40.8.8 Welded Plate Girders
751.40.8.8.1 Design
751.40.8.8.1.1 Design Assumptions & Procedures
Design Unit Stresses
| Reinforcement Concrete | ||
| Reinforcing Steel (Grade 60) | = 24,000 psi, | = 60,000 psi |
| Class B2 Concrete (Superstructure) | = 1,600 psi, | = 4,000 psi |
| Structural Steel: | ||
| Structural Carbon Steel (ASTM A709 Grade 36) | = 20,000 psi, | = 36,000 psi |
| Structural Steel (ASTM A709 Grade 50) | = 27,000 psi, | = 50,000 psi |
| Structural Steel (ASTM A709 Grade 50W) | = 27,000 psi, | = 50,000 psi |
Design Procedure:
Moments and shears by "Variable I" analysis:
- use computer program.
Trial sections from "Preliminary analysis":
- Combination of web depth, flanges and length of plates used shall be the most economical section available with depths compatible with vertical clearance requirements. Web depths in 6" increments are preferred, however other increments may be used when required by the Bridge Memorandum. (See Structural Project Manager)
Flanges:
Minimum flange dimensions = 3/4" x 12" (*).
Increments:
- Thickness 1/8"
- Width 1"
Maximum flange dimensions:
- Reference AASHTO - Table 10.32.1A)
- maximum thickness = 4"
Note: It is preferred office practice to maintain the same flange thickness at as many locations as practical. This can be accomplished by varying the flange width.
(*) For shipping and erection purposes, minimum width of both compression and tension flanges shall not be less than L/85 where L is the shipping length of the girder. This limitation is for preventing out-of-plane distortion of the girder.
Webs:
Web dimensions:
- (Reference AASHTO - Article 10.34 & 10.48)
- ASTM A709 Grade 36 = 3/8" minimum thickness for curved girders and for continuous straight girders.
- ASTM A709 Grade 50W = 3/8" minimum thickness.
- AASHTO - Article 10.3 Case I, Case II or Case III.
- Case I
- Bridges with the truck traffic count of 2500 or more vehicles per day. (One direction)
- Case II
- Bridges with traffic count of 750 or more vehicles per day, and less than 2500 truck traffic count (One direction) per day.
- Case III
- Bridges with traffic count of less than 750 vehicles per day, except when live loading is H20 or greater.
- No Fatigue:
- Bridges with traffic count of less than 75 vehicles per day.
Total Capacity of Exterior Girders:
(Dead Load and Live Load)
- In no case shall an exterior girder have less carrying capacity than an interior girder.
Horizontal Curved Girders Design Procedures (*)
Curved plate girders are to be designed using load factor design criteria. The 1980 AASHTO Guide Specifications for Horizontally Curved Highway Bridges as revised by Interim Specifications for Bridges 1981, 1982, 1984, 1985 and 1986 is to be applied with the USS Highway Structure Design Handbook (\) V-Load method to be used as a working example.
The following procedure may be followed to determine the required cross-section for any system of curved girders with skews less than 46°.
1. Determine the primary moments by the same procedures as for a system of straight girders, using the developed lengths of the curved girders.
2. From primary moments, compute shear loads, , using the formula:
| = Shear loads. M = Primary moments. | |
| = Radius of curvature (outside girder). = Radial distance between inside and outside girders. = Distance between diaphragms measured along axis of outside girder. |
The following coefficients may be applied to "" for the various multiple-girder systems with equal spacing between girders.
| SYSTEM | COEFFICIENT FRACTION |
COEFFICIENT DECIMAL |
| 2 girders | 1 | 1.00 |
| 3 girders | 1 | 1.00 |
| 4 girders | 10/9 | 1.11 |
| 5 girders | 5/4 | 1.25 |
| 6 girders | 7/5 | 1.40 |
| 7 girders | 14/9 | 1.56 |
| 8 girders | 12/7 | 1.72 |
| 9 girders | 15/8 | 1.88 |
| 10 girders | 165/81 | 2.04 |
3. Compute moments
- Reference: USS "Highway Structures Design Handbook" 1965 Edition. (Updated 1986 Volume II Section 6) developed by Richardson, Gordon and Associates in cooperation with Dr. John Scalzi is to be used as a working example.
4. Compute lateral bending moments using the approximate formula:
| = Lateral bending moment | ||
| = The values are approximately equal to the reactions at the supports. | ||
| = Depth of girder between centers of gravity of flanges. | ||
| = Primary moment + Secondary moment. |
5. Determine cross-section required to provide for vertical and lateral forces computed under Items 1 to 4 inclusive. As with any statically indeterminate system it is necessary to make an initial assumption of the required cross-sections and to repeat the calculations one or more times to obtain reasonable agreement between the assumed and required sections.
6. The non-compact section requirement that is to be applied to all sections with the tension flange and the compression flange as to ensure conservative design.
In computing , use to be actual diaphragm spacing for compression and tension stresses.
The value of is to be selected as plus or minus in the equations for to give the worst possible case.
Design and Detail Guides
1. Economic Arrangement of Spans and Depth-to-Spans Ratios
Where there is flexibility in span arrangement, the same guides that apply to economic arrangement of straight girders are equally applicable to curved girders. Similarly the rules used to establish depth-to-span ratios for straight girders usually will apply to curved girders.
2. Spacing of Girders
Spacing depends on the arrangements of diaphragms and bracing. In general, however, it will be found that the most economical arrangement for straight girders will accord very well with the best arrangement for a system of curved girders. The effect of curvature increases in proportion to the square of the span length and decreases in proportion to the radius of curvature and the spacing of girders.
3. Arrangement and Spacing of Diaphragms
The diaphragms shall be placed radially, with a maximum spacing of 15'-0". In order to minimize lateral bending of the girder flanges, the flanges should be as wide as practical.
Sway frame bracing is selected for curved girder system, by same methods as for straight girders.
4. Effect of Lateral Bracing
made in a similar manner as for straight bridges. If lateral Provision for lateral loading on curved girders may be bracing is used in a system of curved girders, the forces resulting from the radial components of flange stress may be carried partially or entirely by the bracing system; when both diaphragms and lateral bracing are used, radial reaction components may be divided between the two systems.
5. Approximate Estimate of Curvature
The following formula may be used in making preliminary approximations of the effect of curvature:
| Note: For "r" refer to paragraph No. 7 | |
| (*) |
| (*) | May be omiteed if supports are on radial lines. |
| % increase in positive moment due to effect of curvature. | |
| Radius of inside girder. | |
| Radius of outside girder. | |
| Distance between points of contraflexure in any pisitive moment area. | |
| Spacing between inside and outside girders. |
In the above form, the formula applies to a two-girder system, but it may be modified by reference to the table of coefficients for multiple-girder systems shown in Item #2. From primary moments, compute shear loads.
The formula applies particularly to positive moment, but for preliminary approximation it may be assumed that the curvature effect on negative moments will be about the same.
6. Design of Diaphragms and Connections
Where the degree of curvature is equal to or under 1° - 30' and when spans are equal to or under 75'-0" in length, the diaphragm and connections shall be the same as for Bridges with straight girders. Where the degree of curvature is over 1°- 30' to 3° or with a span length of more than 75'-0", the diaphragm must be attached to the tension flange. Where the degree of curvature is over 3°, a special design will be required for connection of intermediate diaphragms to flanges.
The maximum allowable diaphragm spacing is 15'-0", regardless of the amount of curvature, or span lengths.
The following applies to those bridges where the special design is to be considered:
Since diaphragm moments due to effect of curvature are a function of the radial component of flange stress, they are directly proportional to the vertical bending moment in the girders.
For exterior girders the moment in the diaphragm equals , in which = vertical bending moment in girder for any particular condition of loading; = diaphragm spacing; = Radius of curvature of girder.
For negative moment over the support, the value used in this equation should be the average moment between a point at the support and a point at the first adjacent diaphragm.
Diaphragm connections may be made directly to the flanges of the girders or through stiffeners, provided details are arranged to adequately transfer radial components of flange stress into the diaphragms.
7. Supports positioned other than on radial lines.
If field conditions permit, the most orderly arrangement for curved girders will be attained by placing the supports on radial lines.
It may be necessary to treat each line of girders independently, first finding the direct loading moments and then correcting for curvature by applying the separate .
8. Transverse stiffeners
The maximum transverse stiffener spacing for curved plate girders is , the web height.
Transverse stiffeners should be placed along the girder length only as far as required by design.
The maximum spacing of the first transverse stiffener at the simple support end of a curved plate girder is .
Reference:
- AASHTO - Article 10.5
- Limit radius of heat curved girders according to AASHTO Article 10.15.
Where the distance between field splices of curved girders exceeds that given by the following formula, a special note shall be placed on the plans.
| = | (*) | |
| = | Allowable distance between field splices, in feet. | |
| = | Allowable fs of flange steel, in psi. e.g. use 20,000 psi for Grade 36 steel. | |
| = | Weight of girder (flanges and web), in pounds per foot. | |
| = | Section Modulus of girder about x-x axis as shown, in inches cubed. |
Note:
If flanges are of different sizes, use smaller Section Modulus.
See Structural Project Manager for allowable overstress.
(*) Derivation
- Positive moment at centerline,
- Substitute mom. in fs equation.
- solve for L
Design Example
ASTM A709 Grade 36 Steel
| |||||||||||
 |
| ||||||||||
| SECTION A-A | |||||||||||
| Weight per Foot of Girder |
| PL 12" x 3/4" = 30.6 lbs./ft. |
| PL 70" x 3/8" = 89.3 lbs./ft. |
| PL 13" x 3/4" = 33.2 lbs./ft. |
| Total = 153.1 lbs./ft. |
From Formula:
(Use 57.5')
Special Note:
Heat curving of girders (Identify) (*) will not be allowed shile in the horizontal position.
(*)Complete underlined portion as required.
Maximum Plate Lengths:
- 80 feet. See Structural Project Manager for use of longer lengths up to 85' for ASTM A709 Grade 50 or ASTM A709 Grade 50W and 100' for ASTM A709 Grade 36.
Minimum Plate Lengths:
- 10 feet. Shop flange splices should be eliminated and extra plate material used when :economy indicates and span lengths permit.
Preliminary Analysis:
- (1) Compute moments from influence lines on basis of "Constant I" analysis and apply the following percentage increase or decrease to non-composite dead load moments.
References may be used in lieu of the above.
| = 1.2 to 1.5 | = 1.2 to 1.5 | ||||||||||||||
|
|
(2) Determine trial sections and plot a rough moment curve to determine location of flange plate cutoffs, if any.
(3) Complete analysis by using computer programs to obtain actual moments and stresses.
Design Stress investigation for Positive Moment Area of Plate Girder Structure
The design stresses are to be checked at the top of flange (steel) and the top of concrete slab in the composible area of Plate Girder Structures to ensure that they are within the allowable stresses.
SECTION A-A
Structure Length
Typical Continuous Steel Structures- Integral End Bents:
Estimated Girder Depth
Based on Three Spans With Ratio N = 1.3±
Continuous Plate Girders HS20 Loading Load Factor
(ASTM A709 Grade 50 or ASTM A709 Grade 50W)
| Initial Estimate (Feet) |
Girder Depths (*) (Inches) |
Structure Depth (**) (Feet) |
| 85 to 104 | 42 | 4.50 |
| 105 to 124 | 48 | 5.00 |
| 125 to 134 | 54 | 5.50 |
| 135 to 144 | 60 | 6.00 |
| 145 to 159 | 66 | 6.50 |
| 160 to 174 | 72 | 7.00 |
| 175 to 184 | 78 | 7.50 |
| 185 to 194 | 84 | 8.00 |
| 195 to 204 | 90 | 8.50 |
Trial steel plate girder depths use program BR109 to check designs and deflections. Web depths may be adjusted by two inch increments.
(*) Bethlehem steel economic study (N = 1.3±). Bethlehem steel provided an economic study of multiple steel girder depths. The study indicated that cheaper designs are obtained by reducing the plate girder depths and reducing the number of stiffeners. The recommended initial estimates above are based on these designs.
(**) Structure depth includes slab and haunch.
A general rule of thumb is to determine the minimum web thickness without stiffeners; then, use a web thickness of one-sixteenth inch less. Match MoDOT requirements for web increments of one-sixteenth inch only.
If two-span structures are used, a deeper web is required. A good estimate is to use six inches additional depth than the above tables for two-span structures.
751.40.8.8.2 Details
751.40.8.8.2.1 Field Flange Splice – Bolted
General
Splices shall be designed using the Service Load Design Method and in accordance with AASHTO Articles 10.18, 10.24 and 10.32 except as noted.
Splices shall be designed to develop 100% of the flange strength by the flange splice plate strength. When the flange section or steel grade changes at a splice, the smaller flange strength shall be used to design the splice. Splice plates shall then match the lower grade used in the flanges.
Minimum Yield Strength and Minimum Tensile Strength
| ASTM A709 Grade 36 | = 36 ksi | = 58 ksi |
| ASTM A709 Grade 50 | = 50 ksi | = 65 ksi |
| ASTM A709 Grade 50W | = 50 ksi | = 70 ksi |
Allowable Steel Stresses
Allowable stresses are determined by AASHTO Table 10.32.1A.
| Allowable tensile stress |
| ASTM A709 | Grade 36 | = 20 ksi |
| ASTM A709 | Grade 50 | = 27 ksi |
| ASTM A709 | Grade 50W | = 27 ksi |
Allowable Bolt Stresses
Splices shall be designed as slip critical connections with Class B surface preparation and oversized holes. Although standard holes are used in the fabrication of flange splices, designing the splices for oversize holes allows for some fabrication and erection tolerances. All splice bolts shall be 7/8" diameter ASTM F3125 Grade A325.
AASHTO Table 10.32.3C specifies = 19 ksi for a class B slip-critical connection. Tables shown in this article are based on 19 ksi that should also be used to design splices not listed in the table.
Although slip-critical connections are theoretically not subject to shear and bearing, they must be capable of resisting these stresses in the event of an overload that causes slip to occur. The allowable shear stress per bolt for bearing is 19 ksi with the threads included and ksi for threads not included.
Flange Strength
The flange strength shall be determined by multiplying the allowable stress of the flange by the area of the flange. The area of the flange shall be taken as the gross area of the flange, except that if more than 15 percent of each flange area is removed, that amount removed in excess of 15 percent shall be deducted from the gross area. Bolt holes are considered to be 1" diameter for the purpose of determining flange area.
Splice Plate Strength
The splice plate strength shall be determined by multiplying the allowable stress of the splice plates by the area of the splice plates. The area of the splice plates shall be taken as the gross area of the splice plates, except that if more than 15 percent of the splice plate area is removed, that amount in excess of 15 percent shall be deducted from the gross area.
Two Row Splices
Splices with two rows of bolts are used with flanges 12 to 13 inches wide. The inner and outer plates may either be the same length or the inner plate may be shorter. This is the case if the end bolts in the splice are only needed to be in single shear. All other bolts will be in double shear. (See Figure 3.42.2.2-1)
Figure 3.42.2.2-1
Four Row Splices
When the width of the flange being spliced is 14 inches or greater, four longitudinal rows of bolts are used. Three variations of the end bolts positioning may be used. In each of these variations, the last two bolts shall be located in the outer rows closest to the edge of the splice plate.
Figure 3.42.2.2-2
Flange Width Transitions
When the width of the flanges being spliced differs by more than 2", the larger flange shall be beveled as shown in Figure 3.42.2.2-3
Figure 3.42.2.2-3
Weight of Splice
When calculating the weight of splice, the following simplified weights shall be used.
Weight of High-Strength bolts (diameter 7/8") = 0.95 lbs/bolt
Unit weight of Structural Steel = 490 lbs/ft3
751.40.8.8.2.2 Field Web Splice – Bolted
General
Splices shall be designed using the Service Load Design Method and in accordance with AASHTO Articles 10.18, 10.24 and 10.32 except as noted.
The web splice consists of 2-Plates:
- Thickness = 5/16" minimum.
- Width = 12-1/2" (18-1/2" if 3 rows of bolts are required).
When the web section or steel grade changes at a splice, the smaller web strength should be used to design the splice.
Minimum Yield Strength and Minimum Tensile Strength
| ASTM A709 Grade 36 | = 36 ksi | = 58 ksi |
| ASTM A709 Grade 50 | = 50 ksi | = 65 ksi |
| ASTM A709 Grade 50W | = 50 ksi | = 70 ksi |
Allowable Steel Stresses
Allowable stresses are determined by AASHTO Table 10.32.1A.
| Allowable bending stress | |
| Allowable shear stress |
| ASTM A709 Grade 36 | = 20 ksi | = 12 ksi |
| ASTM A709 Grade 50 | = 27 ksi | = 17 ksi |
| ASTM A709 Grade 50W | = 27 ksi | = 17 ksi |
Allowable Bolt Stresses
Although standard holes are used in the fabrication of web splices, designing the splices for oversize holes allows for some fabrication and erection tolerances. Web splices required to resist shear between their connected parts are designated as slip-critical connections. Shear connections subjected to stress reversal, or where slippage would be undesirable, shall be slip-critical connections. Potential slip of joints should be investigated at intermediate load stages especially those joints located in composite regions. The resultant force shall be less than the allowable bolt shear force. All splice bolts shall be ASTM F3125 Grade A325 7/8" diameter High Strength Bolts.
= 19 ksi
Bolt Arrangement
The minimum distance from the center of any fastener in a standard hole to a sheared or thermally cut edge shall be 1-1/2 inches for 7/8" diameter fasteners. The minimum distance between centers of fasteners in standard holes shall be three times the diameter of the fastener, but shall not be less than 3 inches for 7/8" diameter fasteners.
Splice Plate Strength
The strength of the splice plates shall be determined by multiplying the allowable stress of the splice plates by the net area of all splice plates. The splice plates net area shall be taken as the gross area of the splice plates minus the bolt holes. Bolt holes are considered to be 1 inch diameter for the purpose of determining splice plate net area. Web splices are designed to develop 75% of net section of the web.
Web Strength
The strength of the web should be determined from the allowable web stress at the "top of web" to account for hybrid sections. Otherwise, the allowable web stress is based on a linear distribution of stress from outside face of flange to "top of web".
Weight of Splice
When calculating the weight of splice, the following simplified weights shall be used.
Weight of High-Strength bolts (diameter 7/8") = 0.95 lbs/bolt
Unit weight of Structural Steel = 490 lbs/ft3
751.40.8.9 Continuous Concrete Slab Bridges
751.40.8.9.1 Slabs
751.40.8.9.1.1 Design Assumptions
| Stresses - | FC | = | 1600 psi | N | = | 8 | (Slab, Integral Column) |
| FC | = | 1200 psi | N | = | 10 | (Open Bent, Footing) | |
| FY | = | 60,000 psi reinforcing steel | |||||
Use "Variable I" analysis for all structures except solid slabs without drop panels.
Use "Constant I" analysis for solid slabs without drop panels.
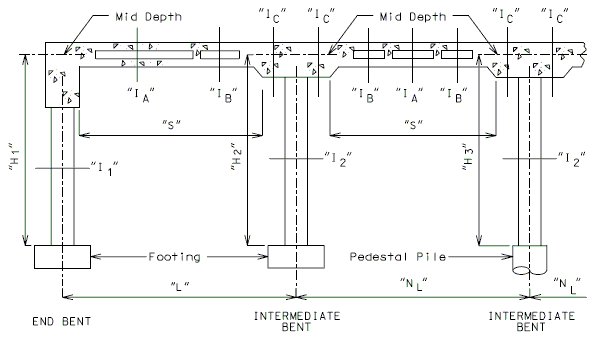
| "L" | = | Design Span |
| "H" | = | Design Height |
| "I" | = | Gross moment of inertia of the full cross-section (Slab minus voids - integral wearing surface not included) ("I1", "IA", etc. suggested I's to be considered.) |
| "S" | = | The effective span length for the use in determining minimum slab thickness under load factor design (AASHTO 8.9). |
Use the same column diameter and spacing for all Intermediate Bents.
Use the same slab thickness for all spans.
| DEGREE OF RESTRAINT - LONGITUDINAL | ||||
| Column Type | Footing Type | Top Column | Bottom Column | |
| INT. BENTS | Integral Column | Spread or Pile | Integral | (**) |
| Integral Column | Pedestal Pile | Integral | (**) | |
| END BENTS | Pinned Column | any | Pinned | (**) |
| Integral Pile | (*) Pinned | |||
| Open Bent with Column | any | Simple | ||
| INT. BENTS | Open Bent with Pile | Simple | ||
| (*) | See EPG 751.40.8.9.2.5 Design Assumptions for Integral Piles. | |
| (**) | Use "Pinned" for Seismic Performance Category A and "Fixed for Seismic Performance Categories B, C & D. (See Structural Project Manager or Liaison) |
751.40.8.9.1.2 Slab Design and Drop Panel
The Slab Depth is based on the following limitations:
| 1. | Vertical Clearance Requirements: see the Bridge Memorandum. | ||||
| 2. | Allowable Depths: | ||||
| A. | Positive Moments - | ||||
| see table of "Available Slab Depths and Void Data", in EPG 751.40.8.9.1.4 Slab Cross Section and Section Properties. | |||||
| B. | Slab Depth controlled by the minimum thickness formula - | ||||
| (Integral wearing surface is included with the total depth provided.) | |||||
| Continuous Spans - AASHTO 8.9 = (S + 10)/30 | |||||
| "S" | may be used as the clear distance between drop panels. | ||||
| Bridges may have two adjacent spans averaged if S2/S1 < 1.5 | |||||
| Simple Spans - AASHTO 8.9 = 1.2 (S + 10)/30 | |||||
| C. | Negative Moments - | ||||
| DROP PANEL DEPTHS | ||
| MIN. | MAX. | |
| Bents in median of dual roadway | 0" or 3" | 13" |
| Other Bents | 0" or 3" | 9" |
| INCREMENTS OF 1" | ||
| APPROXIMATE DROP PANEL WIDTH (FEET) (PARALLEL TO THE CENTERLINE OF ROADWAY) | |||||||
| Bents | Drop Panel Depth | ||||||
| 4" | 6" | 7" | 8" | 9" | 12" | ||
| 3 Span Bridge | 2 & 3 | 6' | 6' | 10' | 8' | 6' | |
| 4 Span Bridge | 2 & 4 | 6' | 6' | 10' | 8' | 6' | |
| 3 | 8' | 10' | 12' | 12' | 12' | 12' | |
| THESE WIDTHS ARE SUGGESTED ONLY AS TRIAL DIMENSIONS FOR DESIGN AND ARE NOT TO BE USED AS LIMITS FOR THE FINAL DESIGN. | |||||||
| 3. | Reinforcing Steel: | ||||
| A. | Positive Moments = Maximum #11 @ 5" cts. | ||||
| B. | Negative Moments = Maximum #11 @ 5" cts., except #14s @ 6" cts., may be used for long spans. | ||||
| 4. | Live Load Deflection - AASHTO 10.6 | ||||
| The deflection due to service live load plus impact shall not exceed 1/800 of the span, except on bridges in urban areas used in part by pedestrains whereon the ratio preferably shall not exceed 1/1000. | |||||
751.40.8.9.1.3 Slab Longitudinal Sections
HOLLOW SLABS
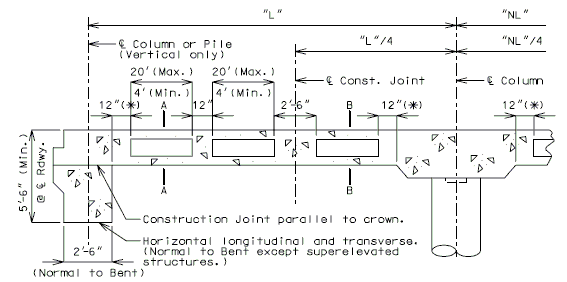
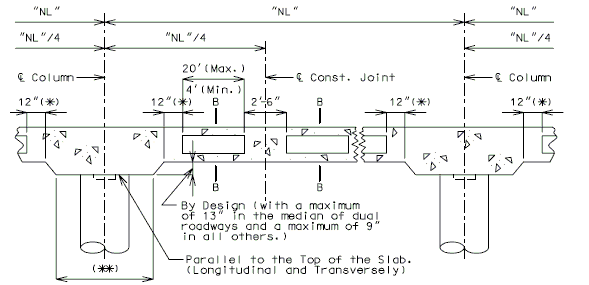
|
(*)Increase to maintain 6" minimum on skews (see detail) |
| (**) By Design (6" increments measured normal to the centerline of bent) (The minimum is equal to the column diameter + 2'-6") | |
| Note: All longitudinal dimensions shown are horizontal (Bridges on grades and vertical curves, included). For Sections A-A and B-B see EPG 751.40.8.9.1.4 Slab Cross Section and Section Properties. |
SOLID SLABS
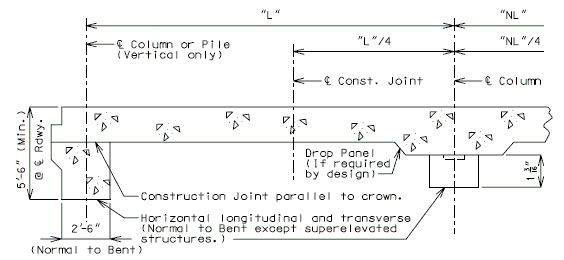
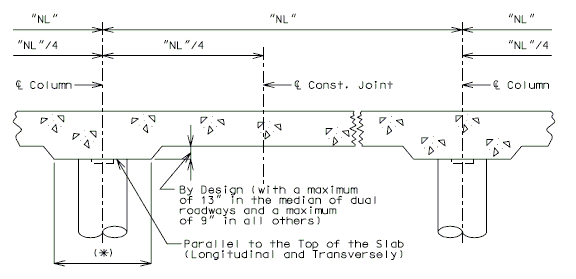
(*) By Design (6" increments measured normal to the centerline of Bent) (The minimum is equal to the column diameter + 2'-6")
Note:
All longitudinal dimensions shown are horizontal (Bridges on grades and vertical curves, included).
751.40.8.9.1.4 Slab Cross Section and Section Properties
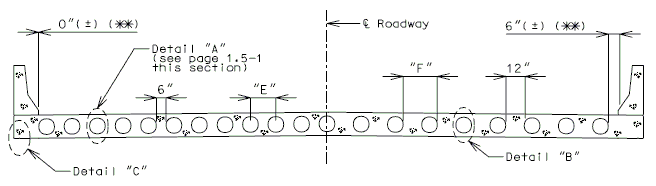
| HALF SECTION A-A CENTER OF SPAN |
HALF SECTION B-B NEAR INTERMEDIATE BENT |
| Notes: | |
| (*) | Increase the Dimension "T" by 1/2" for #14 bars placed in the top or bottom of the slab. |
| Increase the Dimension "T" by 1" for #14 bars placed in the top and bottom of the slab. | |
| ("T" and "D" are based on 3" clearance which includes the integral wearing surface to the top of the longitudinal bar.) | |
| (**) | For Roadways with slab drains, use 10" minimum. For Roadways that require additional reinforcement for resisting moment of the edge beam 20" minimum, refer to EPG 751.40.5.1 Structure with Wearing Surface Slab Drains - Details. |
| (***) | Preferred minimum (Consult the Structural Project Manager prior to the use of a thinner slab.) |
Voided Slab Spans
| Void Dia. (in.) |
Area (sq.ft.) |
Area (sq.in.) |
Moment of Inertia (ft.4) |
Moment of Inertia (in.4) |
Weight (lb./ft.) |
| 8.00 | 0.3490 | 50.2656 | 0.0096 | 201.0624 | 52.35 |
| 9.00 | 0.4417 | 63.6174 | 0.0155 | 322.0630 | 66.26 |
| 10.00 | 0.5454 | 78.5400 | 0.0236 | 490.8750 | 81.81 |
| 12.00 | 0.7854 | 113.0976 | 0.0490 | 1017.8784 | 117.81 |
| 14.00 | 1.0690 | 153.9384 | 0.0909 | 1885.7454 | 160.35 |
| 15.70 | 1.3443 | 193.5932 | 0.1438 | 2982.4242 | 201.66 |
| 16.70 | 1.5211 | 219.0402 | 0.1841 | 3818.0075 | 228.17 |
| 18.70 | 1.9072 | 274.6465 | 0.2894 | 6002.5789 | 286.09 |
| 20.85 | 2.3710 | 341.4310 | 0.4473 | 9276.7336 | 355.65 |
751.40.8.9.1.5 Slab Reinforcement
HOLLOW SLABS
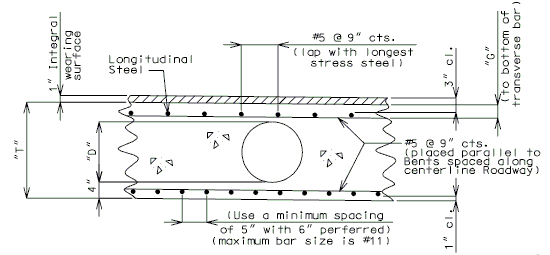
(POSITIVE MOMENT)
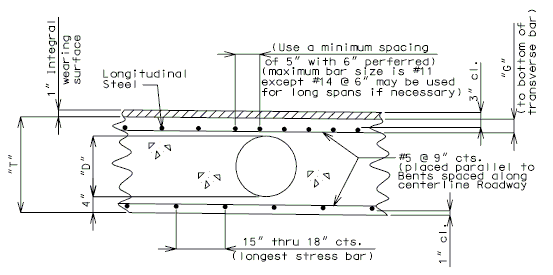
(NEGATIVE MOMENT)
| Longitudinal Reinforcement (Largest Bar) |
"G" |
| #8 | 3-5/8" |
| #9 | 3-3/4" |
| #10 | 3-7/8" |
| #11 | 4" |
| #14 | 4-3/8" |
Moment Curves
| 1. | Determine reinforcing steel from the sum of the dead loads and the live loads + impact (working stress design) or design in accordance with AASHTO Article 8.16 and 8.9 (load factor design). |
| 2. | Determine the cut-off points for the stress bars in sets of 2 or 3. Maximum length = 60'-0", see AASHTO Article 8.24 for extension of reinforcement. |
| 3. | Determine the drop panel width: |
| Minimum width = Column diameter plus 2~6". Maximum width = (Parallel to the centerline of roadway) as determined by deign). | |
| In general, the width of the drop panel normal to centerline bent should be adjusted to 6" increments. |
SOLID SLABS (BOTTOM)
Use AASHTO 3.24.10 Distribution Reinforcement shall be a percentage of positive moment reinforcement (% = 100/√S, with a maximum of 50%).
EDGE BEAM
| Positive Moment: | ||
| The bridge curb is not to be used in determining the resisting moment of the edge beam. | ||
| Dead Load: | Use the same distribution as for the slab design. Use for simple spans 0.1 PS. | |
| Live Load + I: AASHTO Article 3.24.8 | ||
| Use for negative moment on continuous spans 0.1 PS. Use for positive moment on continuous spans 0.08 PS. | ||
| Where | P = Wheel load in pounds, see EPG 751.40.8.5.1.1 Cantilever Moment. | |
| S = Span in feet | ||
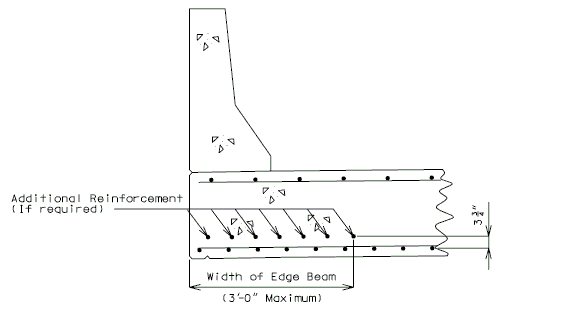
751.40.8.9.1.6 Shear
Shear Loads
The shear in the Hollow Slab should be computed for all loadings H20 and over.
Distribution of Loads
Use the same distribution for the dead and live load as was used for the moment.
Unit Shear Stress
| Load Factor: | |||
| Shear Stress | = | ||
| Working Stress: | |||
| Shear Stress | = | ||
| Where "d" = effective depth, = 0.85 for shear | |||
Allowable Shear Stress
| Load Factor: | |
| Where Vc = shear strength provided by concrete | |
| Working Stress: | |
| Where Vc = Allowable shear stress carried by concrete | |
If shear stress (load) exceeds the allowable shear use one or more of the following solutions.
- Eliminate some voids and replace remainder.
- Shorten alternate voids
- Use shear reinforcing in the critical zone.
Note:
Consider a voided slab the same as a regular slab as it pertains to the minimum stirrups (AASHTO - Article 8.19).
i.e. The minimum stirrups are not required if the shear stress is less than allowable.
751.40.8.9.1.7 Camber Deflection
Ultimate Deflection:
Compute the "ultimate deflection" at 0.2 points of the spans for the dead loads without the 35# future wearing surface.
Ultimate deflection (long term) = elastic deflection x 3
| Ec (Elastic Modulus) = | psi (districts 1 and 4) |
| psi (remainder of districts) |
The modulus of elasticity for the use in a continuous structure analysis computer program should be determined as follows:
| = | ||
| = | ||
| = | ||
| Where: | ||
| = | deflection. | |
| = | Ultimate deflection | |
| = | Elastic deflection |
Example No. 1
(Assume bridge is in District 8)
| = | ||
| = |
Therefore, use 2 \times 106 psi for modulus of elasticity in the structure analysis computer program to get ultimate deflection. (*)
Example No. 2
(Assume bridge is in District 1)
| = | ||
| = |
Therefore, use psi for modulus of elasticity in the structure analysis computer program to get ultimate deflection. (*)
(*) Gives long term deflection as output.
751.40.8.9.1.8 Slab Construction Joint Details
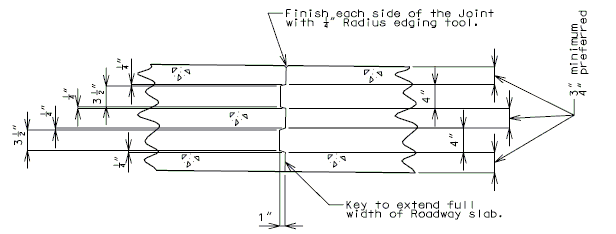
(FOR SLAB DEPTHS 17" OR MORE)
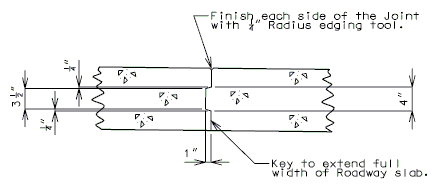
(FOR SLAB DEPTHS 16½" OR LESS)
751.40.8.9.2 End Bents
751.40.8.9.2.1 Pile Cap Bents
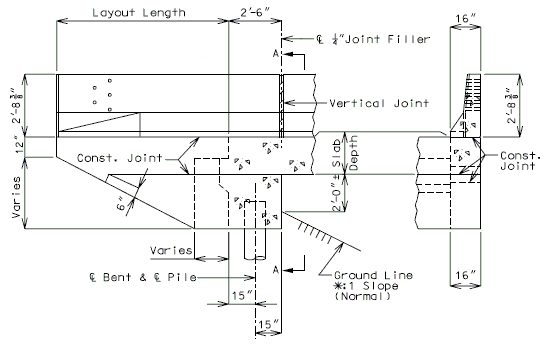
| SECTION THRU WING | SECTION A-A |
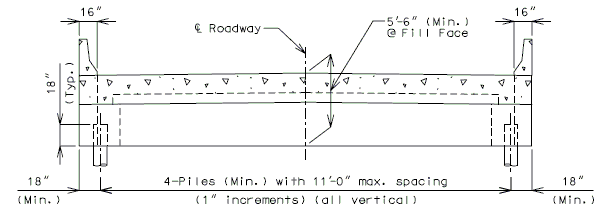
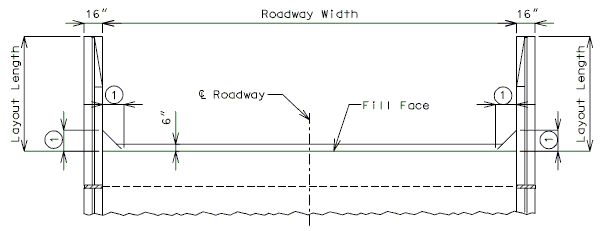
| (1) Wing brace details. | 
|
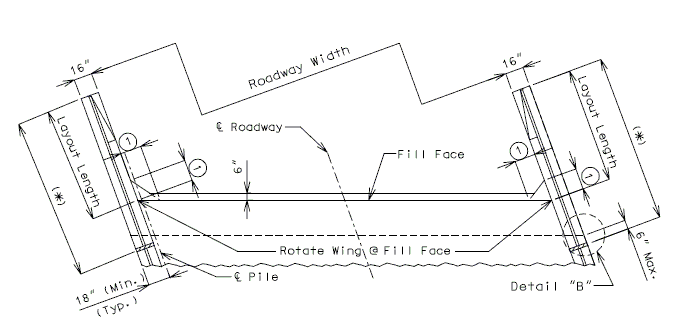
751.40.8.9.2.2 Integral Column Bents
SEISMIC PERFORMANCE CATEGORY A
(PINNED COLUMN AT TOP AND BOTTOM)
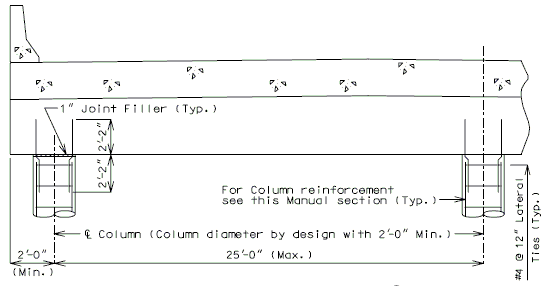
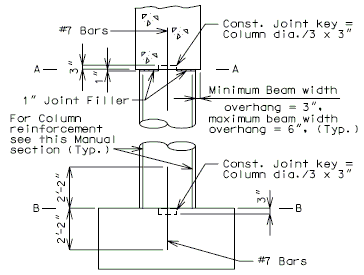 |
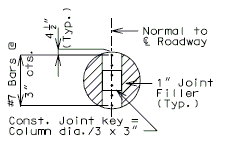
|
| SECTION A-A | |
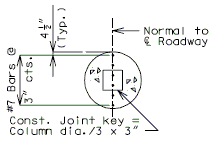
| |
| PINNED COLUMN | SECTION B-B |
Note: If the columns at an end bent have excessive moments due to shortness of the Column or length of the span, they should be detailed as "pinned" and designed for vertical reactions only.
SEISMIC PERFORMANCE CATEGORIES B, C & D
(PINNED COLUMN AT TOP, FIXED COLUMN AT BOTTOM)
For pinned column conditions at the top, see the above details.
For fixed column conditions at the bottom and column reinforcement details.
Note: For details not shown, see integral pile cap details.
751.40.8.9.2.3 Reinforcement - Pile Cap Bents
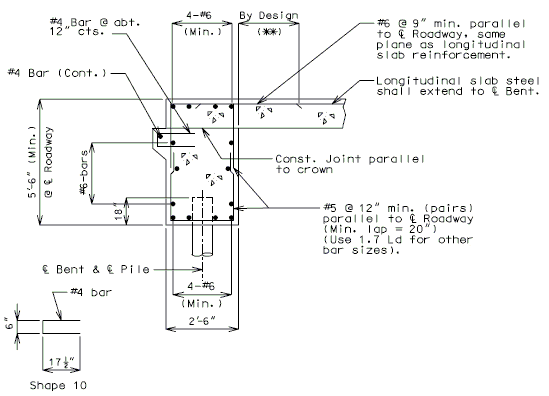
(Slab depth less than 16")
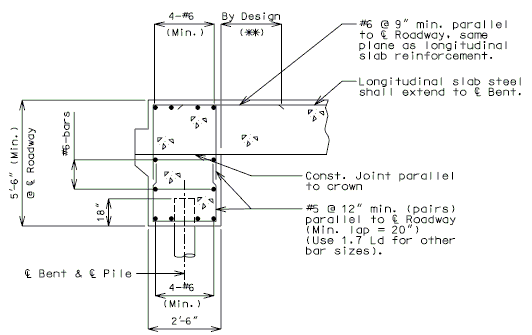
(Slab depth 16" or more)
(**) Development length for top bar minimum.
751.40.8.9.2.4 Reinforcement - Wing
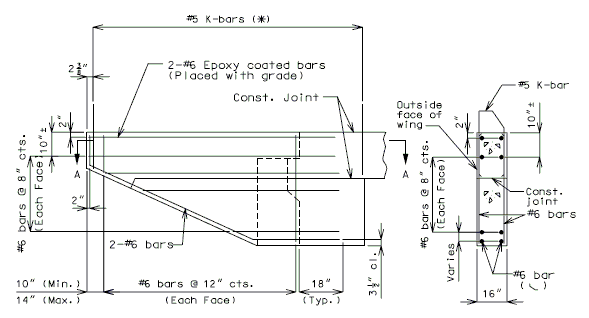
| ELEVATION OF WING | PART SECTION THRU WING |
| (*) Clip K bars as required to maintain minimum clearance at bottom of wing. | |
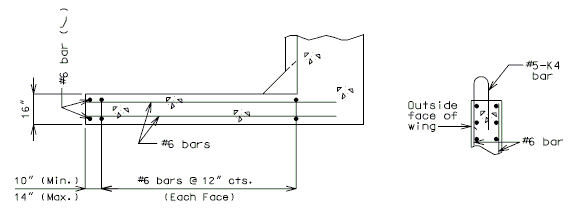
| SECTION A-A (K-bars not shown for clarity) |
PART SECTION THRU END OF WING |
Note: See _____ for barrier railing details and spacing of K-bars.
751.40.8.9.2.5 Design Assumptions for Integral Piles
Seismic Performance Category A
Piles may be considered as "pinned" (for superstructure) at the pile cap and designed for vertical loads only unless they fall under the following general conditions in which case they should be checked for the loadings as specified for columns.
| 1. | Height from centerline of slab to "pin" is less than 15'. |
| The location of the pinned joint is arbitratily taken as about 1/3 of the length of long piles or at a point about 10' below the natural ground line. | |
| 2. | Piles having a large gross moment of inertia (cast-in-place concrete) gross I of steel BP = I x n. |
| 3. | The number of piles used on a fairly long structure is small. |
Seismic Performance Categories B, C & D
Piles shall be checked for combined axial and bending stresses for seismic loading conditions. For AASHTO group loads I thru VI as applicable, follow criteria noted above for seismic performance category A.
751.40.8.9.3 Intermediate Bents
751.40.8.9.3.1 Integral Bents
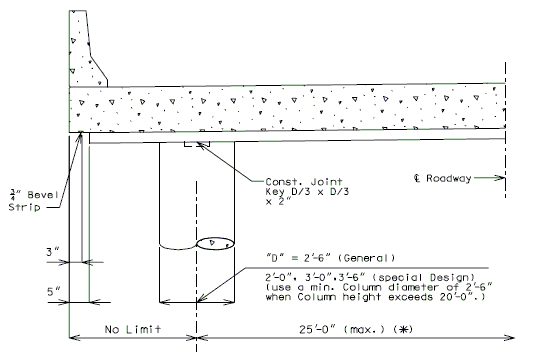
(*) 25'-0" is the max. column spacing allowed. However, the footing pressure may be the controlling factor for the column spacing. It is suggested that a rough check be made of the footing pressure before the spacing is definitely established.
In congested areas, when it is desired to keep the number of columns to a min., larger column spacings may be desirable. (consult the Structural Project Manager).
In general, use two 2'-6" columns for Roadways thru 44'-0" and additional 2'-6" columns for wider Roadways.
SEISMIC PERFORMANCE CATEGORY A
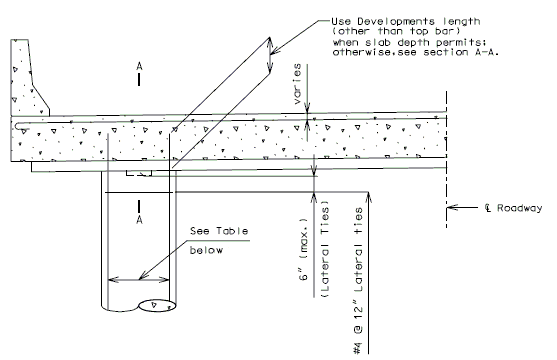
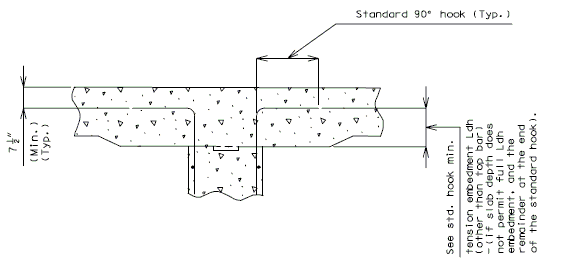
751.40.8.9.3.2 Integral Column Bent with Drop Panel
 |
ATTENTION DETAILER: When detailing Int. Bents on SPS the Section thru drop panel shall be drawn to appropriate grade. |
| PART SECTION |
| PART SECTION A-A (FLAT) |
PART SECTION A-A (GRADE OR V.C.) D = Diameter of Column |
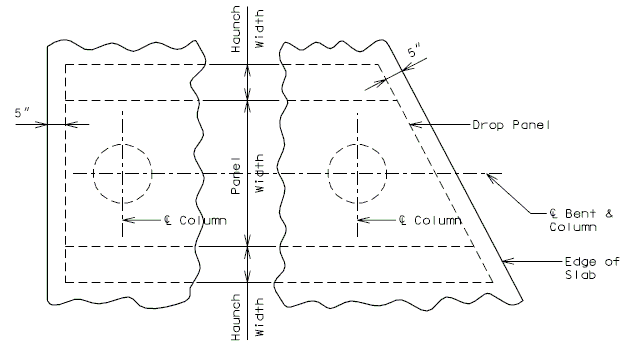
| PART PLAN - SQUARE | PART PLAN - SKEWED |
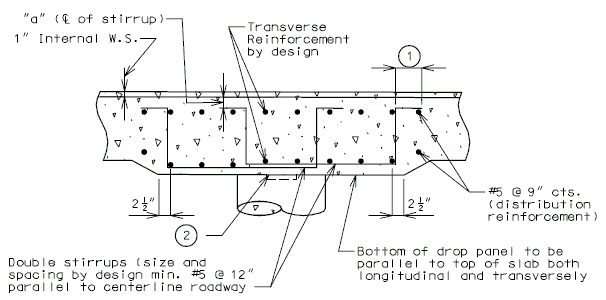
|
 |
For Reference Only | ||||||||
|
(*) Based on 3" clearance and #6 stirrups, (includes Integral W.S.) to top longitudinal bar.
(1) Standard 90° Hook.
(2) Const. joint key D/3 x D/3 x 2", D = Diameter of Column
751.40.8.9.3.3 Integral Pile Cap Bents with Drop Panel
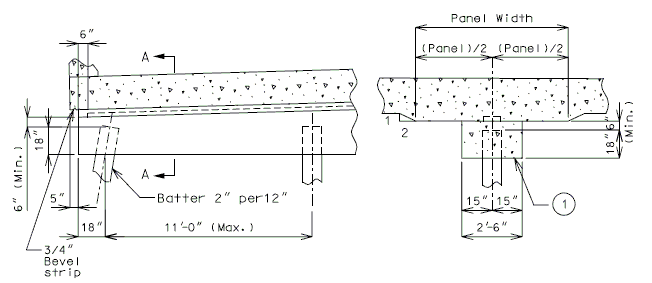
| PART SECTION | PART SECTION A-A (FLAT) |
| Bottom or drop panel to be parallel to top of slab both transversely and longitudinally. | 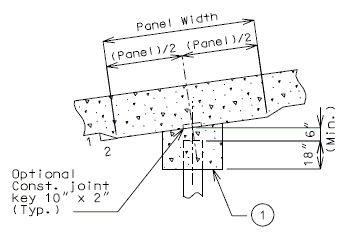
|
| (1)Horizontal except for superelevated structures. | |
| (2) Use 3" Min. clip on beam for skews above 35°. | |
| PART SECTION A-A (GRADE OR V.C.) |
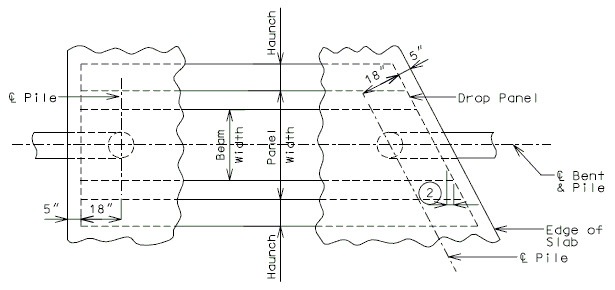
| PART PLAN - SQUARE | PART PLAN - SKEWED |
REINFORCEMENT
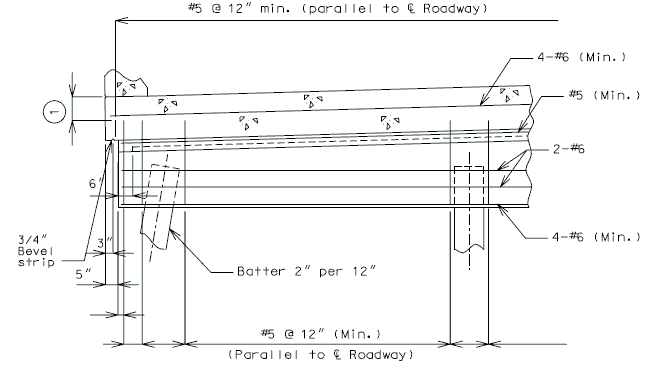
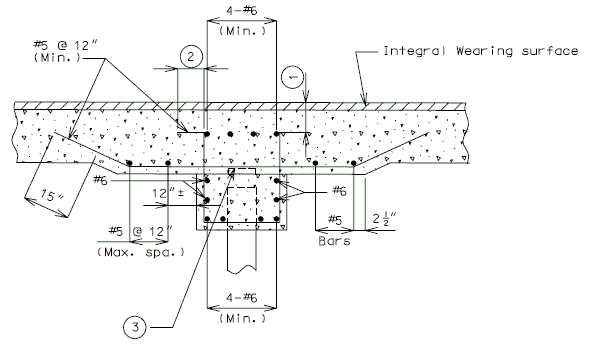
(1) Use 5 1/4" for computing length of stirrup bar. Do not detail on plans.
(2) Standard 90° hook.
(3) Optional Const. Joint Key 10" x 2"
751.40.8.9.3.4 Integral Pile Cap Bents without Drop Panel
REINFORCEMENT
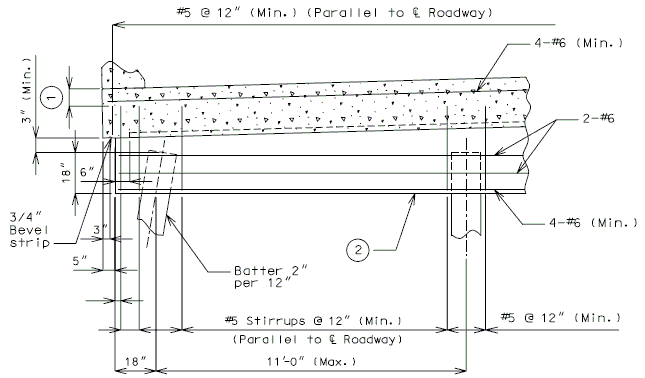
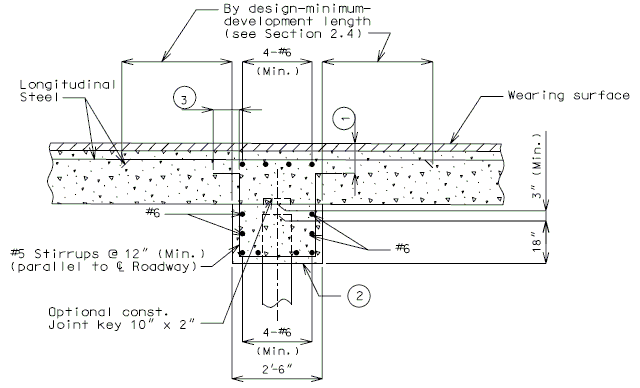
(1) Use 5 1/4" for computing length of stirrup bar. Do not detail on plans.
(2) Horizontal except for superelevated structures.
(3) Standard 90° hook.
751.40.8.9.3.5 Pile Footing Design and Details
(1) GENERAL
Number, size and spacing of piling shall be determined by computing the pile loads and applying the proper allowable overstresses.
Cases of Loading (AASHTO Article 3.22)
Group I maximum vertical loads.
Group IV temperature and shrinkage moments with applicable vertical loads.
1983 AASHTO guide specifications for seismic design of highway bridges. (See chapter 4 for earthquake loads combined with applicable vertical loads.) (*) (See Structural Project Manager or Liaison)
Internal stresses including the position of the shear line shall then be computed.
Long narrow footings are not desirable and care should be taken to avoid the use of an extremely long footing 6~0" wide when a shorter footing 8'-3" or 9'-0" wide could be used.
When using the load factor design method for footings, design the number of piles needed based on the working stress design method.
ASSUMPTIONS (Bents with 2 or more columns)
SEISMIC PERFORMANCE CATEGORY A
- Dead and live load moments will be 25% of the moments used for slab and top of Column design.
- Temperature moments shall be 50% of the moment at top of Column.
- Column reinforcement to be same as that required at top of Column. Footing dowel's to be #5 bars, same number as column bars.
- Footings to be proportioned for conditions as specified. Do not use ratio of bent height as specified for Intermediate Bents for longitudinal footings dimensions.
SEISMIC PERFORMANCE CATEGORIES B, C & D
- For Seismic Performance categories B, C & D, the connection between the bottom of Column and the footing is a fixed connection.
- Footing design is based on (Seismic Design of Beam-Column Joint).
(*) The design of all bridges in seismic performance B, C & D are to be designed by earthquake criteria in accordance with EPG 751.9 Bridge Seismic Design.
(2) PILE LOADS
- P = N/n ± M/S
- P = Pile Loads
- N = Vertical Loads
- n = number of piles
- M = overturning moment
- if minimum eccentricity controls the moment in both directions, it is necessary to use the moment in one direction (direction with less section modulus of Pile group) only for the footing check.
- S = Section Modulus of pile group
AASHTO GROUP I AND IV LOADS
Maximum P = Pile Capacity Minimum P = 0
Tension on a pile will not be allowed for any combination of forces.
Overstress reduction will not be used for loading minimums.
EARTHQUAKE LOADS
POINT BEARING PILES
(**) Maximum P = Pile capacity x 2
- (I.E. for HP 10 x 42 piles, maximum P = 56 x 2 = 112 tons/pile).
Minimum P = Use allowable uplift force specified for piles in EPG 751.39 Seal Course.
(**) Two (2) is our normal factor of safety. Under earthquake loadings only the point bearing pile and rock capacities are their ultimate capacities.
FRICTION PILES
Maximum P = Pile capacity
(3) INTERNAL STRESSES
- A) Shear Line
- B) Bending
- C) Distribution of Reinforcement
- D) Shear
751.40.8.9.3.6 Pedestal Pile
GENERAL
No concrete bell shall be used without approval of Structural Project Manager or Liaison.
SEISMIC PERFORMANCE CATEGORY A
- Assume column to be "pinned" for belled footing sitting on rock. All loads will be axial.
- Assume column to be fixed for pedestal pile embedded in rock.
- All earth loads within the diameter of belled footing, or pedestal pile if there is no bell, above ground line shall be included in footing design.
SEISMIC PERFORMANCE CATEGORY B, C & D
See (Seismic Design).
DETAILS
SEISMIC PERFORMANCE CATEGORY A
| Diameter of Shaft |
Minimum Bell Diameter |
Maximum Bell Diameter |
Minimum (*) Reinf. |
Cubic Yards Concrete per ft. |
| 2'-0" | 2'-4" | 6'-0" | 8-#7 | 0.1164 |
| 2'-6" | 2'-10" | 7'-6" | 8-#9 | 0.1818 |
| 3'-0" | 3'-6" | 9'-0" | 11-#9 | 0.2618 |
| 3'-6" | 4'-0" | 10'-6" | 14-#9 | 0.3563 |
| 4'-0" | 4'-6" | 12'-0" | 19-#9 | 0.4654 |
| 4'-6" | 5'-0" | 13'-0" | 24-#9 | 0.5890 |
| 5'-0" | 5'-6" | 14'-0" | 29-#9 | 0.7272 |
| 5'-6" | 6'-0" | 15'-0" | 35-#9 | 0.8799 |
| 6'-0" | 6'-6" | 16'-0" | 41-#9 | 1.0472 |
Concrete Quantities shown in table are per linear foot of shaft only. Bell Quantities are not included.
(*) Amount of reinforcing may be increased from that shown to meet the individual job requirements.
Minimum reinforcement meets AASHTO Spec. 8.18 for reinforcement of compression members.
DETAILS
SEISMIC PERFORMANCE CATEGORY B, C & D
| Diameter of Shaft |
Minimum (*) Reinf. |
Cubic Yards Concrete per ft. |
| 2'-0" | 8-#7 | 0.1164 |
| 2'-6" | 8-#9 | 0.1818 |
| 3'-0" | 11-#9 | 0.2618 |
| 3'-6" | 14-#9 | 0.3563 |
| 4'-0" | 19-#9 | 0.4654 |
| 4'-6" | 24-#9 | 0.5890 |
| 5'-0" | 29-#9 | 0.7272 |
| 5'-6" | 35-#9 | 0.8799 |
Concrete Quantities shown in table are per linear foot of shaft only.
(*) Amount of reinforcing may be increased from that shown to meet the individual job requirements.
Minimum reinforcement meets AASHTO Spec. 8.18 for reinforcement of compression members.
(**) Stay in place casing may be used in place of spirals for column diameters greater than 4 foot.
751.40.8.10 Prestressed Concrete I-Girders
751.40.8.10.1 Design
751.40.8.10.1.1 Girder Design
Geometric Dimensions
Girder Analysis (Continuous Span Series)
Stresses due to dead load weight of slab, girder, diaphragms, haunch and forms will be based on simple spans from centerline to centerline of bearings.
Stresses due to dead load weight of curbs, parapet, rails, future wearing surface and outlets will be based on continuous composite spans with loads equally distributed to all girders. The span lengths used in these computations will be based on the distance from the centerline of the bearing at the End Bent to the centerline of the Int. Bent, and from centerline of Int. Bent to centerline of Int. Bent.
Stresses due to live load plus impact will be based on continuous composite spans whose lengths are described above for curbs, etc.
The analysis will be made on the basis of transformed areas of all steel (both strands and bars) in the section using concrete with = 6.
In composite design, allowances shall be made for the difference in modulus of elasticity of slab and girder by using the effective slab area as specified for concrete T-Beams as given in the current AASHTO Specifications, multiplied by the factor . The area shall include the transformed area of all longitudinal reinforcing bars within the effective width. The 1" integral wearing surface shall not be used in the effective slab depth.
Effective Flange Width
The effective flange width for Beam Types 2,3,4 & 6 should be calculated using AASHTO 8.10.1. For Beam Type 7, the effective flange width should be calculated using AASHTO 9.8.3.
Continuity at Intermediate Supports
Continuity will be obtained at intermediate supports by pouring a concrete diaphragm monolithic with the deck slab and encasing the prestressed girders. Reinforcing bars will tie the slab, diaphragms and girders together.
Reinforcing bars, = 60,000 psi, will be placed in the deck slab for tensile steel.
The ultimate negative moments should be 2.17 times the maximum live load moments including impact and 1.3 times moments for future wearing surface and dead load of barrier or railing.
The area of longitudinal reinforcing steel at the centerline of the intermediate bent should be determined on the basis of a cracked section. This area of reinforcing bars is to be provided by adding additional bars between the normal longitudinal bars at the top of the slab. #8 maximum bar size for additional bars over bents.
These special negative moment reinforcing bars should be ended by one of the following criteria (whichever is greater):
- Where the stress on the normal longitudinal reinforcing bars does not exceed 24,000 psi. as based on a cracked section, plus 15 bar diameters or development length.
- Not closer to the centerline of the intermediate bent than 1/10 of the span. (8' min.)
The concrete stress at the bottom of the girder should be checked at a point 70 strand diameters plus 9 inches from the centerline of the intermediate bent to see that the total compressive stress due to prestress and negative moment does not exceed 3,000 psi. (AASHTO. 9.7.2)
The positive moment at the intermediate bent should be provided for by extending the top two rows of the top strands (both straight or deflected) and if available, the number of bottom strands indicated in tables below bent to form a right angle hook.
Design of Negative Moment Reinforcement
Since most of the dead load moments are carried by the beam acting as a simple span, the negative design moment over piers is the live load plus impact moment. In most designs, the dead load applied after continuity is achieved should also be considered in the negative design moment. The effect of initial precompression due to prestress in the precast girders may be neglected in the negative moment computation of ultimate strength if the maximum precompression stress is less than and the continuity reinforcement is less than 1.5 percent.
It will usually be found that the depth of the compression block will be less than the thickness of the bottom flange of the precast girder. For this reason, the negative moment reinforcement required can be determined by assuming the beam to be a rectangular section with a width equal to the bottom flange width of the girder. Due to the lateral restraint of the diaphragm concrete, ultimate negative compression failure in the PCA tests always occurred in the girders, even though the diaphragm concrete strength was about 1000 psi less than that of the girder concrete for this reason, it is recommended that the negative moment reinforce-ment be designed using the compressive strength of the girder concrete.
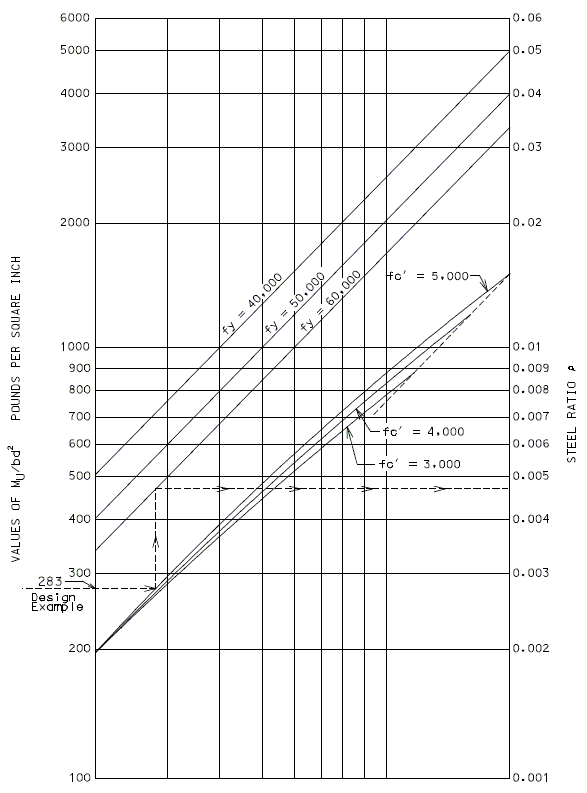
| Web Thickness (Inches) |
Number of Bottom Strands for Positive Moment Connection (C) for Closed Diaphragms | ||||
|---|---|---|---|---|---|
| Beam Type 2 or Modified |
Beam Type 3 or Modified |
Beam Type 4 or Modified |
Beam Type 6 or Modified |
Beam Type 7 or Modified | |
| 6 | 6 | 8 | 10 | -- | 18 |
| 6 1/2 | -- | -- | -- | 14 | -- |
| 7 (A) | 8 | 10 | 10 | -- | -- |
| 7 1/2 (B) | -- | -- | -- | 16 | -- |
| 8 (A) | 8 | 10 | 12 | -- | -- |
| 8 1/2 (B) | -- | -- | -- | 16 | -- |
| Web Thickness (Inches) |
Number of Bottom Strands for Positive Moment Connection (C) for Open Intermediate Diaphragms with Continuous Superstruecture | ||||
|---|---|---|---|---|---|
| Beam Type 2 or Modified |
Beam Type 3 or Modified |
Beam Type 4 or Modified |
Beam Type 6 or Modified |
Beam Type 7 or Modified | |
| 6 | 12 | 16 | 16 | -- | 22 |
| 6 1/2 | -- | -- | -- | 22 | -- |
| 7 (A) | 12 | 16 | 16 | -- | -- |
| 7 1/2 (B) | -- | -- | -- | 22 | -- |
| 8 (A) | 12 | 16 | 16 | -- | -- |
| 8 1/2 (B) | -- | -- | -- | 22 | -- |
| (A) | Modified Beam Type 2, 3 or 4. |
| (B) | Modified Beam Type 6. |
| (C) | If available, otherwise bend all bottom strands. |
Negative Moment Bar Cut-Off (Working Stress Controlling)
Area of slab bars required and stress in the slab bars are printed in program BR200.
Determine stress of the area of slab bars input into program at a point where the area required is larger than that input.
Interpolate along a straight line to where the stress is 24,000 psi.
Note: Negative moment bar computations use a cracked section analysis to determine stresses.
751.40.8.10.1.2 Allowable Concrete Stresses
The following criteria is shown for clarity and is in accordance with AASHTO 9.15.
- = 5,000 psi, = 4,000 psi
A. Temporary stresses before losses except as noted:
- Compression... (*)
- Tension
- Precompressed tensile zone ....................
- No temporary allowable stresses are specified. See paragraph "B" below.
- In tension areas with no bonded reinforcement...
- Where the calculated tensile stress exceeds this value, bonded reinforcement shall be provided to resist the total tension force in the concrete computed on the assumption of an uncracked section. The maximum tensile stress shall not exceed...
- Precompressed tensile zone ....................
B. Stresses at service loads after losses:
- Compression...
- Tension in the precompressed tensile zone...
- (a) For members with bonded reinf. (**)...
- (b) For members without bonded reinf...
- Tension in other areas
- Tension in other area is limited by the allowable temporary stresses specified in "A" above.
C. Cracking stress:
- Modulus of rupture from tests or (for normal weight concrete)...
D. Negative moment stresses in girders made continuous after deadload of slab is in place:
- Tension in negative moment reinforcement... = 60,000 psi, = 24,000 psi
- Compression in concrete at bottom of girder... = 5,000 psi,
(*) BR200 allows 2% overstress
(**)Strands qualify if not debonded at ends.
751.40.8.10.1.3 Prestress Loss and Prestress Camber
| Reduce to: | = Shrinkage | |
| = Elastic Strain | ||
| = Concrete Creep | ||
| = Steel Creep |
| = | |
| = (Approximate Estimate) | |
| = (Approximate Estimate) | |
| = Concrete stress at centroid of P/S steel at point considered due to P/S and dead load at release. | |
| = (Assume ) | |
| = (Estimate average) | |
| = Concrete stress at centroid of P/S Steel (due to dead load)(Assume fcds = 1/2 fc) | |
| = Initial stress in P/S steel | |
| = | |
| = | |
| = (AASHTO 9.16.2.1) | |
| = |
Total loss due to all causes, except friction, is 34.22 ksi. (Friction losses are applied to post-tensioned girder only.) Use 8.84% for initial loss and 8.84% for final loss for design.
= initial loss
= final loss
= total loss
In the above design example, if tension exceeds AASHTO Specifications, (425 psi for 5,000 psi concrete) the girder will have to be modified to limit stress to 425 psi.
| = 6,000 psi | |
| = 4,500 psi | |
| Grade 270 low relaxation strands | |
| = (Estimated average) | |
| = | |
| = | |
| AASHTO 9.16.2.1.3: (approximate estimate) | |
Reduce to:
| = (estimated average) | |
| = |
= Initial stress in low relaxation strands stressed to 75% of ultimate (*)
= 270,000 psi \times 75% = 202,500 psi
= total loss except friction
Use 9.44% for initial loss and 9.44% for final loss.
= initial loss
= final loss
= total loss
P/s force initial =
P/s force final =
(*) Suggested by FHWA: when using 3/8" round strands, max. , whichever is smaller. Larger initial stresses will cause debonding.
Prestress Concrete Girder Formula for Stress Calculation
(-) Tension; (+) Compression
Temp. Stress
| Allow Top | tension for | |
| Bottom | compression for |
- Temp. Top =
- Temp. Bottom =
Design Load Stress
| Allow Top | compression for | |
| Bottom | tension for |
- Top final =
- Bottom final =
- 0.153 sq. in. = Area of one 1/2 inch strand
- 270 ksi = f's = Ult, Str. P/S Strand
- 202.5 ksi = 0.75 (270) = Initial steel stress
- 0.0884 = 8.84% Initial loss - low relaxation
- 0.0884 = 8.84% Final loss - low relaxation
- 4 Str. 2 Draped
- 202.5 (0.153) = 30.98 kips/Str. P/s force
- 6 Strands (30.98) = 185.90 P/s force
| = Area Composite | |
| = Area Girder | |
| = Eccentricity of prestress force of composite section | |
| = Eccentricity of prestress force of non-composite section | |
| = Composite dead load moment | |
| = Girder dead load moment | |
| = Live load + impact moment | |
| = Slab + diaphragm moment | |
| = Prestress forces in girder | |
| = Composite section modulus at bottom of girder | |
| = Non-composite section modulus at bottom of girder | |
| = Composite section modulus at top of girder | |
| = Non-composite section modulus at top of girder |
Prestress Camber
Reference: Computer Program BR139B
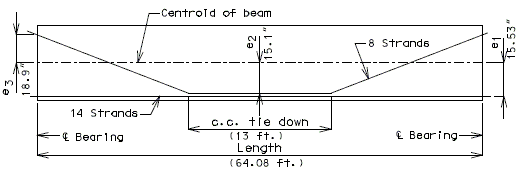
Used to resist uplift before beam is set on bent.
Used after beam is in place.
| Mult. factor |
| ||||||||||||||||||
| = 1.77 | |||||||||||||||||||
| =2.718 | |||||||||||||||||||
| = \varepsilon\ creep \times E_{28\ days} | |||||||||||||||||||
| = (See page 3 PCA design of precast prestressed concrete girders. Use 40% factor based on creep at erection for 28 days.) | |||||||||||||||||||
The following formulas are used to determine:
- Camber due initial strand stress (inch),
- deflection due beam weight (inch),
- camber due strands, beam weight and 28 day creep (inch),
- camber L/4 due strands, beam weight and 28 day creep (inch),
- deflection due to slab weight (inch),
- camber centerline due strands, beam weight, 28 day creep, slab and diaphragm (inch), and
- camber quarterpoint due strands, beam weight, 28 day creep, slab and diaphragm (inch).
Formulas used:
Positive deflect up
Negative deflect down
Beam weight camber
Slab weight camber
Force straight strands (1/2" low relaxation strands)
Force draped strands ( 1/2 " low relaxation strands)
| = dist. centroid beam to centroid straight strand (in.) | |
| = dist. centroid beam to low centroid draped at center of beam (in.) | |
| = dist. centroid beam to up centroid draped at end of beam (in.) | |
| = length (ft.) (cneterline bearing to centerline bearing). | |
| = moment of inertia (in.2) non-transformed. | |
| = moment of inertia (in.2) transformed. | |
| = concentrated loads due to variable slab thickness on each end. | |
| = dist. from centerline brg. to Ps. | |
| = concentrated load due to diaphragm at center of span (kips) | |
| = uniform beam load (kips/ft.) | |
| = uniform slab load (kips/ft.) | |
| = factor for 28 day creep | |
| = modulus of elasticity corresponding to initial girder concrete strength | |
| = modulus of elasticity corresponding to final girder concrete strength |
Note: Compute and show on plans camber at 1/4 points for bridges with spans less than 75', 1/10 points for spans 75' and over.
751.40.8.10.1.4 Superstructure Design
Live Load Distribution
The live load distribution to girders may be assumed to be the same as the AASHTO distribution for concrete floors on steel I-Beam stringers. These factors may be found in EPG 751.40.8.2 Distribution of Loads.
Ultimate Load Capacity
The ultimate load capacity shall be not less than 1.3 times (the weight of the girder plus the weight of the slab and diaphragms plus the weight of the future wearing surface) plus 2.17 times the design live load plus impact.
Ultimate Strength
The ultimate moment on a prestressed girder as determined in accordance with the ultimate load capacity indicated above, shall not be greater than the ultimate strength determined as follows:
| Where | Where | |
 |
| |
or |
Use the lesser in each case |
or |
Where:
| = Area of p/s strands in bottom flange | |
| , , & | = as shown above |
| = Ultimate strength of p/s strands | |
| = Ultimate strength of slab concrete = 4,000 psi |
Maximum Prestressing Steel Area
- When
- When
In lieu of the above, AASHTO - Article 9.17 & 9.18 may be used. (This is the method used by computer program BR200)
751.40.8.10.1.5 Web Reinforcement
(5" Min. - 21" Max. bar spacing for #4 bars) (5" Min. - 24" Max. bar spacing for #5 bars)

(*) Prestressed concrete members shall be reinforced for diagonal tension stresses. Shear reinforcement shall be placed perpendicular to the axis of the member. The formula to be used to compute areas of web reinforcement is as follows:
- Where but not more than
- But shall not be less than .
(**) Since large moments and large shears occur in the same area of the girder near the interior supports, the AASHTO formula (AASHTO - 9.20 -Shear) for computing the area of web reinforcement has been modified. The formula to be used to compute areas of web reinforcement near interior supports is as follows:
The value "jd" is the distance from the slab reinforcement to the center-of-gravity of the compression area under ultimate loads.
Use #4 shear reinforcement when possible. Alternate B1 bar will not work with #5.
Anchorage Zone Reinforcement - AASHTO Article 9.21.3
The following detail meets the criteria for anchorage zone reinforcement for pretensioned girders (AASHTO Article 9.21.3) for all MoDOT standard girder shapes.
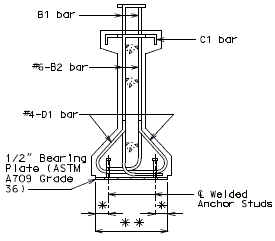
|
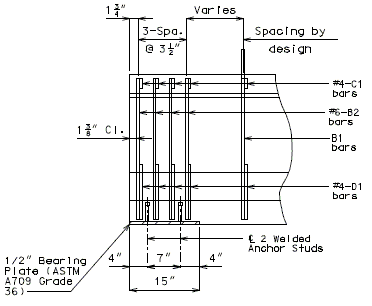
|
| * | 2 3/4" (Type 2, 3 & 4) 5 1/4" (Type 6) |
| ** | 15 1/2" (Type 2, 3 & 4) 22 1/2" (Type 6) |
Sole Plate Anchor Studs
The standard 1/2" sole plate will be anchored with four 1/2" x 4" studs.
Studs shall be designed to meet the criteria of AASHTO Div. I-A in Seismic Performance Category C or D.
Stud capacity is determined as follows:
Where:
| = no. of studs | |
| = area of stud | |
| = yield strength of stud (50 ksi) | |
| = Allowable Shear in Pins AASHTO Table 10.32.1A | |
| = seismic overload factor |
If required, increase the number of 1/2" studs to six and space between open B2 bars. If this is still not adequate, 5/8" studs may be used. The following table may be used as a guide to upper limits of dead load reactions:
| The minimum 3/16" fillet weld between the 1/2" bearing plate and 1 1/2" sole plate is adequate for all cases. |
| ||||||||||||||||||||||
751.40.8.10.1.6 Strands – Miscellaneous
Detensioning
In all detensioning operations the prestressing forces must be kept symmetrical about the vertical axis of the member and must be applied in such a manner as to prevent any sudden or shock loading.
General Information
Splicing:
One approved splice per pretensioning strand will be permitted provided the splices are so positioned that none occur within a member. Strands which are being spliced shall have the same "Twist" or "Lay". Allowance shall be made for slippage of the splice in computing strand elongation.
Wire failure:
Failure of one wire in a seven wire pretensioning strand may be accepted, provided that, it is not more than two percent of the total area of the strands.
Sand Blasting:
On structures where it is questionable as to the clarity of areas to be sandblasted: show limits of sandblasted area in a plan view of details on girder ends (bent sheet). However, generally, sandblasting is covered by Missouri Standard Specification 705.4.14.
751.40.8.10.2 Length
751.40.8.10.2.1 Structure Length
(Integral End Bents)
(Non-Integral End Bents)
751.40.8.10.3 Miscellaneous Details
751.40.8.10.3.1 Shear Blocks
A minimum of two Shear Blocks 12" wide x ![]() high by width of diaphragm, will be detailed at effective locations on open diaphragm bent caps when adequate structural restraint cannot be provided for with anchor bolts.
high by width of diaphragm, will be detailed at effective locations on open diaphragm bent caps when adequate structural restraint cannot be provided for with anchor bolts.
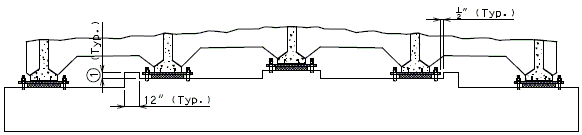
| Height of shear block shall extend a minimum of 1" above the top of the sole plate. |
751.40.8.10.3.2 Anchor Bolts
Simple Spans
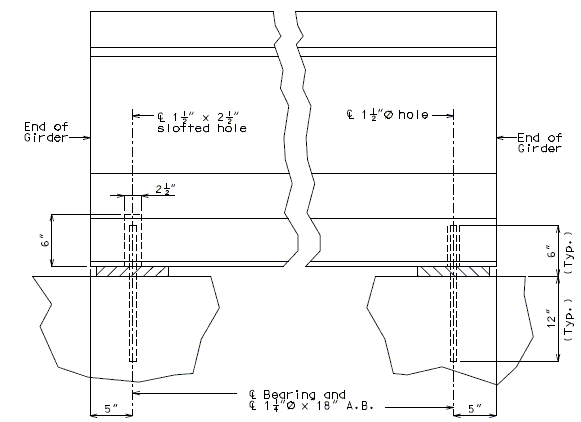
| |
| Expansion | Fixed |
|---|---|
| Part Elevation | |
| Note: | It is permissible for the reinforcing bars and or the strands to come in contact with the materials used in forming A.B. holes. |
| If A.B. holes are formed with galvanized sheet metal, the forms may be left in place. | |
| Hole (1 1/2" round) to be grouted with approved non-shirk grout. |
751.40.8.10.3.3 Dowel Bars
|
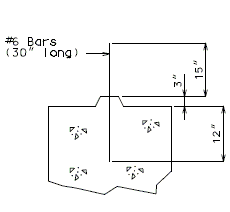
|
| Part Elevation (Fixed Bent) (*) |
Section A-A (*) |
|---|
| (*) | Details shown are for SPC A and B only. |
Dowel bars shall be used for all fixed intermediate bents under prestressed superstructures.
Seismic Performance Category A:
- Use #6 Bars @ 18" Cts. for dowel bars.
Seismic Performance Category B:
- Dowel bars shall be determined by design. (#6 Bars @ 18" Cts. minimum)
- Design dowel bars for shear using service load design.
- Allowable stresses are permitted to increase by 33.3% for earthquake loads.
Seismic Performance Categories C & D:
- See Structural Project Manager.
751.40.8.10.3.4 Expansion Device Support Slots
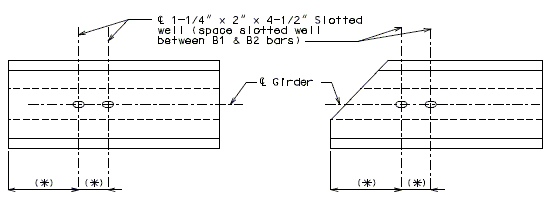
|
| Part Plan of P/S Concrete I-Girder @ Expansion Device End |
|---|
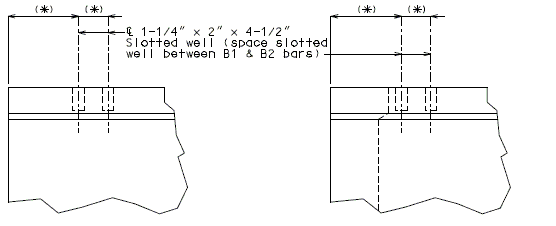
|
| Part Elevation of P/S Concrete I-Girder @ Expansion Device End |
| (*) | Show these dimensions on the P/S concrete girder sheet. |
751.40.8.11 Open Concrete Intermediate Bents and Piers
751.40.8.11.1 Design
751.40.8.11.1.1 General and Unit Stresses
GENERAL
Use Load Factor design method, except for footing pressure and pile capacity where the Service Load design method shall be used.
In some cases, Service Load design method may be permitted on widening projects, see Structural Project Manager.
The terms, Intermediate Bents and Piers, are to be considered interchangeable for EPG 751.40.8.11 Open Concrete Intermediate Bents and Piers.
DESIGN UNIT STRESSES
(1) Reinforced Concrete
Class B Concrete (Substructure) = 1,200 psi = 3,000 psi Reinforcing Steel (Grade 60) = 24,000 psi = 60,000 psi n = 10 (AASHTO Article 8.7.1) (*)
(2) Reinforced Concrete (**)
Class B-1 Concrete (Substructure) = 1,600 psi = 4,000 psi Reinforcing Steel (Grade 60) = 24,000 psi = 60,000 psi = 8 (AASHTO Article 8.7.1) (*)
(3) Structural Steel
- Structural Carbon Steel (ASTM A709 Grade 36)
- = 20,000 psi, = 36,000 psi
(4) Overstress
- The allowable overstresses as specified in AASHTO Article 3.22 shall be used where applicable for Service Load design method.
(*) Use
(**) May be used for special cases, see Structural Project Manager.
751.40.8.11.1.2 Loads
(1) Dead Loads
(2) Live Loads
- As specified on the Bridge Memorandum.
- Impact of 30% is to be used for the design of beam, web supporting beam and top of columns. No impact is to be used for bottom of column, tie beam or footing design.
(3) Wind and Frictional Forces
(4) Temperature and Shrinkage
- The effect of normal and parallel components to the bent shall be considered. When bearings with high friction coefficients are used or for long bridge lengths, the columns and footings are to be analyzed for moments normal to the bent due to the horizontal deflection of the top of the bent.
(5) Buoyancy
- If specified by the Structural Project Manager, or by the Bridge Memorandum.
(6) Earth Pressure
- Bents are to be analyzed for moments due to equivalent fluid pressure on columns and web where the ground line at time of construction, or potential changes in the ground line, indicate.
(7) Earthquake
- See Structural Project Manager or Liaison.
(8) Special Stability Situations
- When indicated by the Bridge Memorandum or by the Structural Project Manager, piers must be analyzed for special loadings as directed (i.e., differential settlement).
(9) Collision
- Where the possibility of collision exists from railroad traffic, the appropriate protection system, for example Collision Wall, shall be provided (See the Bridge Memorandum).
(10) Collision Walls
- Collision walls are to be designed for the unequal horizontal forces from the earth pressure, if the condition exists (See the Bridge Memorandum). The vertical force on the collision wall is the dead load weight of the wall (*). If a bent has three or more columns, design the steel in the top of the wall for negative moment.
(*) For footing design, the eccentricity dead load moment due to an unsymmetrical collision wall shall be considered.
751.40.8.11.1.3 Distribution of Loads
(1) Dead Loads
- Loads from stringers, girders, etc. shall be concentrated loads applied at the centerline of bearing. Loads from superstructure, such as concrete slab spans, shall be applied as uniformly distributed loads.
(2) Live Loads
- Loads from stringers, girders, etc., shall be applied as concentrated loads at the intersection of centerline of stringer and centerline of bent.
(3) Wind and Frictional Forces
(4) Temperature
- Apply at the top of the substructure beam.
(5) Earth Loads
- (a) Vertical
- Vertical earth loads on tie beams shall be applied as uniform loads for a column of earth equal to 3 times the width of the beam. The weight of earth for footing design shall be that directly above the footing, excluding that occupied by the column.
- The earth above the seal courses shall be considered in computing pile loads. Refer to the Design and Dimension of the Pile Footings portion of EPG 751.40.8.13 Concrete Pile Cap Non-Integral End Bents or EPG 751.36 Driven Piles.
- (b) Horizontal
(*) A factor of 2.0 is applied to the moment to allow for the possibility of the column esisting earth pressure caused by the earth behind the column twice the column width.
(6) Earthquake Loads
- See Structural Project Manager or Liaison.
(7) Seal Course
- The weight of the seal course shall not be considered as contributing to the pile loads, except for unusual cases.
751.40.8.11.1.4 Types of Design
TYPES OF DESIGN
Rigid frame design is to be used for the design of Intermediate Bents and Piers.
The joint between the beam and column, and web or tie beam and column,
is assumed to be integral for all phases of design and must be analyzed
for reinforcement requirements as a "Rigid Frame".
The joint between the column and footing is assumed to be "fixed",
unless foundation fexibility needs to be considered (consult Structural
Project Manager for this assessment).
If the distance from the ground line to the footing is large (*),
consideration shall be given to assuming the column to be "fixed" at a
point below the ground line.
(*) When the distance from the ground line to the top of footing is 10' or more, the unsupported height and the fixed point may be measured from the bottom of the beam to the ground line plus 1/2 of the distance from the ground line to the top of the footing.
UNSUPPORTED HEIGHT
Unsupported height is the distance from the bottom of the beam to the top of the footing.
SINGLE COLUMN
Use rigid frame design with the column considered "fixed" at the bottom for all of the conditions.
COLUMN DIAMETER CHANGE
Use a change in column diameter as required by the Bridge Memorandum or column design.
COLUMN SPACING (TRIAL)
(Except Web Supporting Beam type)
Estimate centerline-centerline column spacing for a two column bent as 72% of the distance from the centerline of the outside girder to the centerline of the outside girder.
A three column bent spacing estimation is 44% of the centerline-centerline outside girder spacing.
751.40.8.11.2 Reinforcement
751.40.8.11.2.1 Hammer Head Type
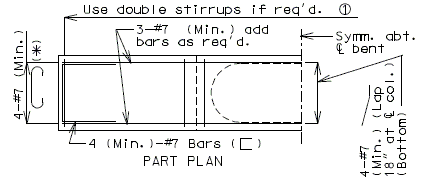 |
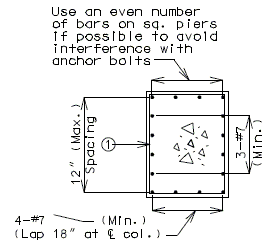
|
| PART PLAN | SECTION A-A |
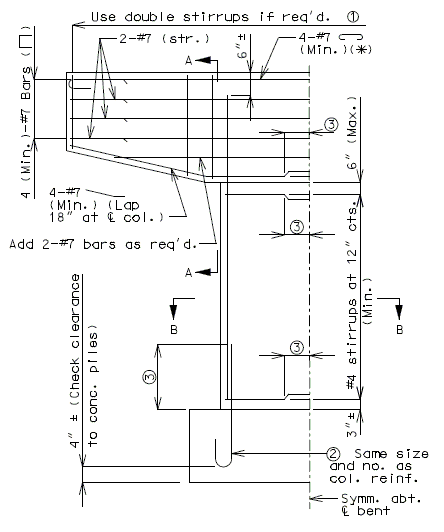 |
Note: When an expansion device in the slab is used at an intermediate bent, all reinforcement located entirely within the beam shall be epoxy coated. See details of protective coating and sloping top of beam to drain. |
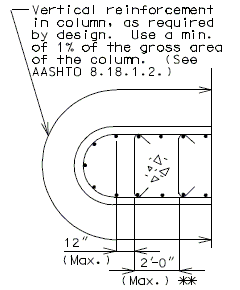
| |
| PART ELEVATION | PART SECTION B-B |
(*) Add hooked reinforcement as required by design.
(**) See AASHTO Article 8.18.2.3.4 for tie requirements.
![]() All stirrups in beam to be the same size bar. (Use a min. spacing of 5" (6" for double stirrups), minimum stirrups are #4 at 12" cts., and maximum
stirrups are #6 at 6" cts.)
All stirrups in beam to be the same size bar. (Use a min. spacing of 5" (6" for double stirrups), minimum stirrups are #4 at 12" cts., and maximum
stirrups are #6 at 6" cts.)
Locate #4 bars (┌─┐) under bearings if required. (Not required for P/S Double-Tee Girders.)
![]() See development length (Other than top bars) or standard hooks in
tension, Ldh.
See development length (Other than top bars) or standard hooks in
tension, Ldh.
751.40.8.11.3 Pile Footings
751.40.8.11.3.1 Design and Dimensions
GENERAL
- Number, size and spacing of piling shall be determined by computing the pile loads and applying the proper allowable overstresses.
- Cases of Loading: (AASHTO Article 3.22)
- Group I and Group II maximum vertical loads (refer to distribution of loads, this Section).
- Group III thru VI wind and/or temperature moments with applicable vertical loads.
- Internal stresses including the position of the shear line shall then be computed.
- Long narrow footings are not desirable and care should be taken to avoid the use of an extremely long footing 6~0" wide when a shorter footing 8'-3" or 9'-0" wide could be used.
- Footings are to be designed for the greater of the minimum moment requirements at the bottom of the column, or the moments at the bottom of the footing.
- When using the load factor design method for footings, design the number of piles needed based on the working stress design method.
PILE LOADS
- Pile Loads - Vertical Loads - Number of Piles - Overturning Moment If minimum eccentricity controls the moment in both directions, It is necessary to use the moment in one direction (direction with less section modulus of pile group) only for the footing check. - Section Modulus of Pile Group
- (A) AASHTO Group I thru VI Loads as applicable
- Maximum = Pile Capacity
- Minimum (zero)
- Tension on a pile will not be allowed for any combination of forces.
- Pile design force shall be calculated with consideration of AASHTO percentage overstress factors.
- (B) Earthquake Loads
See Structural Project Manager or Liaison before using the following seismic information.
- Point Bearing Pile
- Maximum (**)
- (i.e., for HP 10 X 42 piles, Max. tons/pile)
- Minimum = Allowable uplift force specified for piles in this
- Section under Seal Course Design.
- (**) Two "2" is our normal factor of safety. Under earthquake loadings only the point bearing pile and rock capacities are their ultimate capacities.
- Friction Piles
- Maximum = Pile Capacity
- Minimum = Allowable uplift force specified for piles in this
- Section under Seal Course Design.
- See combined axial & bending stresses in Cast-In-Place friction piles in liquefaction areas.
(1) Shear Line
| If the shear line is within the column projected, the footing may be considered satisfactory for all conditions and standard #6 hairpin bars shall be used.
|
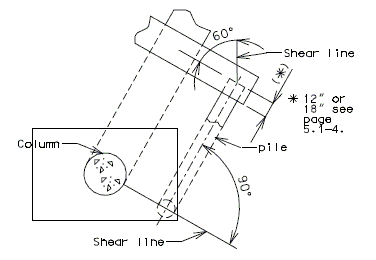
|
(2) Bending
The critical section for bending shall be taken at the face of the columns (concentric square of equivalent area for round columns).
The reinforcement shall be as indicated for reinforced footings, except that the standard #6 hairpin bars may be used for small footings if they provide sufficient steel area.
(3) Distribution of Reinforcement
Reinforcement in Bottom of Footing
Reinforcement shall be distributed uniformly across the entire width of footing in the long direction. In the short direction, the portion of the total reinforcement given by AASHTO Equation 4.4.11.2.2-1 shall be distributed uniformly over a band width equal to the length of the short side of the footing, .
- Band Width Reinforcement =
- where
The remainder of the reinforcement required in the short direction shall be distributed uniformly outside the center band width of footing.
Reinforcement in Top of Footing
Reinforcement in the top of the footing shall be provided based on a seismic analysis for Seismic Performance Categories B, C and D. This reinforcement shall be at least the equivalent area as the bottom steel in both directions. The top steel shall be placed uniformly outside the column.
(4) Shear
(AASHTO Article 8.15.5 or 8.16.6)
The shear capacity of footing in the vicinity of concentrated loads shall be governed by the more severe of the following two conditions.
(i) Beam shear
Critical Section at "d" distance from face of column.
| b = Footing Width Service Load | 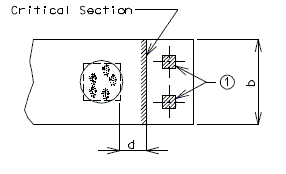
|
| Service Load | |
| Load Factor | |
| PART PLAN OF FOOTING |
|---|
(ii)Peripheral Shear
Critical Section at "d/2" distance from face of column.
| Service Load | 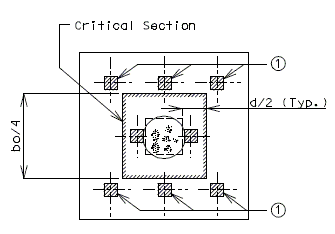
|
| Load Factor | |
| PART PLAN OF FOOTING |
|---|
If shear stress is excessive, increase footing depth.
| Piles to be considered for shear. (Center of piles are at or outside the critical section.) |
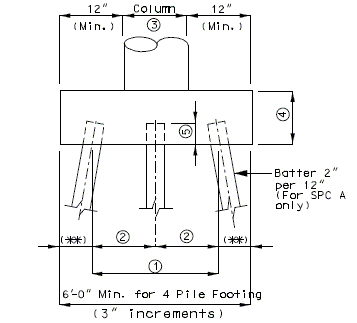 |
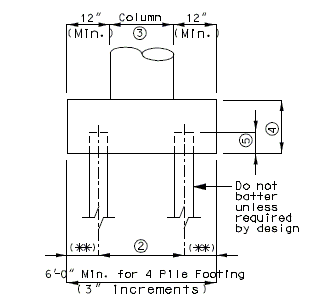
|
| SIDE ELEVATION | FRONT ELEVATION |
|---|
| Min. = 1/8 x (Distance from top of beam to bottom of footing.) | |
| 3'-0" (Min.) & 6'-0" (Max.) for steel HP piles, 14" CIP piles. AASHTO Article 4.5.6.4 shall be considered if piles are situated in cohesive soils. | |
| 3D (Min.) and 6D (Max.) for 20" and 24" CIP piles. (D = pile diameter) | |
| Indicates column diameter, or column length or width on a hammer head pier. | |
| Min. = 2'-6" or column diameter (*) (Or width) for friction piles for SPC A. | |
| Min. = 3'-0" or column diameter (*) (Or width) for steel piles for SPC A. | |
| Min. = 3'-0" or column diameter (*) (Or width) for friction piles for SPC B,C,& D. | |
| Min. = 3'-6" or column diameter (*) (Or width) for steel piles for SPC B, C & D. | |
| 12" for seismic performance category A and 18" for SPC B, C, & D. | |
| (*) | For column diameters 4'-0" and greater use a 4'-0" min. footing thickness. |
| (**) | Use 18" for steel HP piles, 14" CIP piles, prescase and prestress piles. |
TYPICAL PLAN OF
3 PILE FOOTINGS
(minimum pile spacings)
NOTES:
Use 3- piles on exterior foorings only.
Use only HP 10 x 42 or friction piles on three pile footings.
TYPICAL PLAN
STAGGERED PILE
(7 Pile footings shall not be used.)
| If horizontal thrust requires pile batter- consult the Structural Project Manager. |
(*) The maximum pile spacing is 4'-0".
751.40.8.11.3.2 Reinforcement
Unreinforced Footing - Use only in Seismic Performance Category A
|
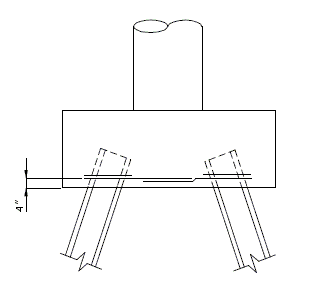
|
| Elevation (3 Pile Footing) |
Elevation (4 Pile Footing |
|---|---|
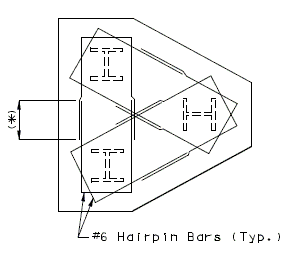
|
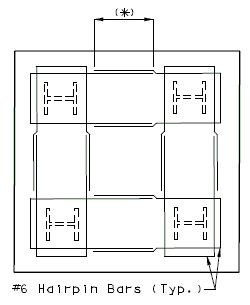
|
| Plan (3 Pile Footing) |
Plan (4 Pile Footing |
| (*) | See lap splice class C (Other than top bars). |
| Notes: | Reiforcement not required by design. Hairpins are sufficient for renforcing requirements. |
| The minimum percentage of reinforcement, "P" , is not required to be met, unless scour is anticipated. | |
| Use for all types of piling, except timber. |
Reinforced Footing - Seismic Performance Category A
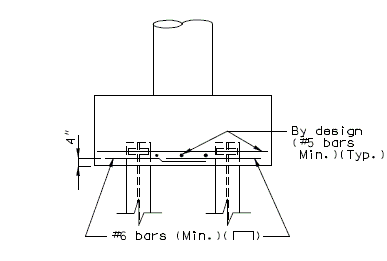
|
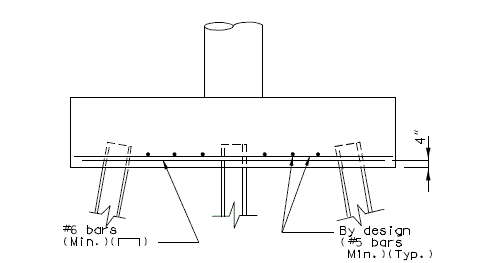
|
| Front Elevation | Side Elevation |
|---|---|
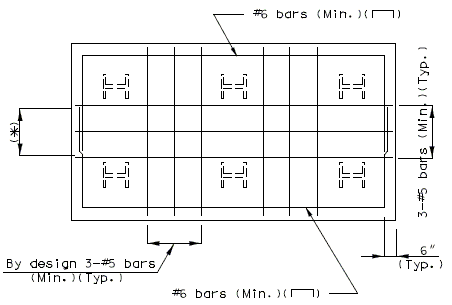
| |
| Plan | |
| (*) | See lap splice class C (Other than top bars). |
| Note: | The maximum size of stress steel allowed is #8 bars. |
Reinforced Footing - Seismic Performance Categorys B, C & D
See Structural Project Manager or Liaison before using the following seismic details.
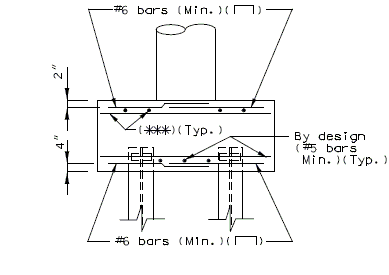
|
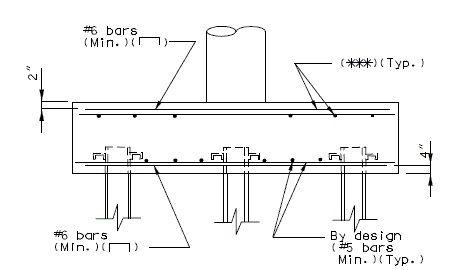
|
| Front Elevation | Side Elevation |
|---|---|
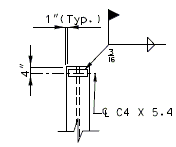
|
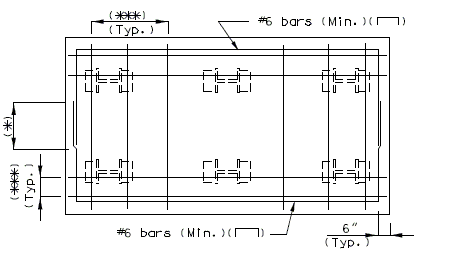
|
| Typical Detail Pile Channel Shear Connector | |
| Plan Showing Top Reinforcement | |
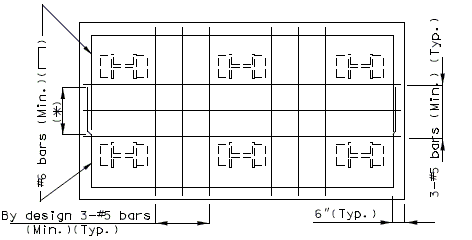
| |
| Plan Showing Bottom reinforcement | |
| (*) | For reinforcement in top of the footing, see lap splice class C (Top bars). |
| (**) | Place the top reinforcement uniformly outside the column. |
| (***) | Use same area of steel in the top of the footing as is required for the bottom. |
| Notes: | For reinforcement in bottom of the footing, see lap splice Class C (Other than top bars). |
| The maximum size of stress steel allowed is #8 bars. | |
| Unreinforced footings shall not be used in seismic performance categories B, C & D. |
751.40.8.11.4 Spread Footings
751.40.8.11.4.1 Design and Dimensions
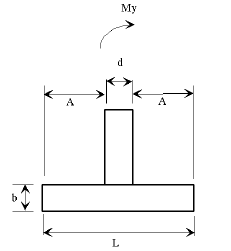
|
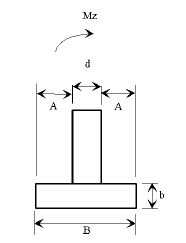
|
| Side Elevation | Front Elevation |
|---|
| d | = column diameter |
| L | = footing length |
| b | = footing depth |
| B | = footing width |
| A | = edge distance from column |
The calculated bearing pressure shall be less than the ultimate capacity of the foundation soil. The ultimate capacity of the foundation soil can be conservatively estimated as 2.0 times the allowable bearing pressure given on the Bridge Memorandum. The analysis method of calculating bearing pressures is outlined in the following information.
Dimensional Requirements
| L - | Minimum of 1/6 x distance from top of beam to bottom of footing (3" increments); |
| B - | Minimum footing width is column diameter + 2A, (3" increments); |
| A - | Minimum of 12"; |
| b - | Minimum of 30" or column diameter, Maximum of 72" at 3" increments; (for column diameters 48" and greater use a 48" minimum footing depth.) |
Size
The size of footing shall be determined by computing the location of the resultant force and by calculating the bearing pressure.
Long, narrow footings are to be avoided, especially on foundation material of low capacity. In general, the length to width ratio should not exceed 2.0, except on structures where the ratio of the longitudinal to transverse loads or some other consideration makes the use of such a ratio limit impractical.
Location of Resultant Force
The location of the resultant force shall be determined by the following equations.
The Middle 1/3 is defined as:
The Middle 1/2 is defined as: and
The Middle 2/3 is defined as: and
The following table specifies requirements for the location of the resultant force.
| Soil Type | Resultant Location Group I - VI | Resultant Location Earthquake Loads Categories B, C and D |
|---|---|---|
| Clay, clay and boulders, cemented gravel, soft shale with allowable bearing values less than 6 tons, etc. | middle 1/3 | middle 1/2 |
| Rock, hard shale with allowable bearing values of 6 tons or more. | middle 1/2 | middle 2/3 |
Bearing Pressure
The bearing pressure for Group I thru VI loads shall be calculated using service loads and the allowable overstress reduction factors as specified in AASHTO Table 3.21.1A. The calculated bearing pressure shall be less than the allowable pressure given on the Bridge Memorandum.
The bearing pressure for Earthquake Loads in Categories B, C, and D shall be calculated from loads specified in AASHTO Division I-A Seismic Design, Sections 6.2.2, 7.2.1, and 7.2.2. The seismic design moment shall be the elastic seismic moment (EQ) divided by the modified response modification factor R'. The modified seismic moment shall then be combined independently with moments from other loads:
Group Load =
Where:
| = dead load | |
| = buoyancy | |
| = stream flow pressure | |
| = elastic seismic moment | |
| = earth pressure | |
| = R/2 for category B | |
| = 1 for categories C and D | |
| = Response Modification Factor | |
| = 5 for multi-column bent | |
| = 3 for single-column bent | |
The calculated bearing pressure shall be less than the ultimate capacity of the foundation soil. The ultimate capacity of the foundation soil can be conservatively estimated as 2.0 times the allowable bearing pressure given on the Bridge Memorandum. The analysis method of calculating bearing pressures is outlined in the following information.
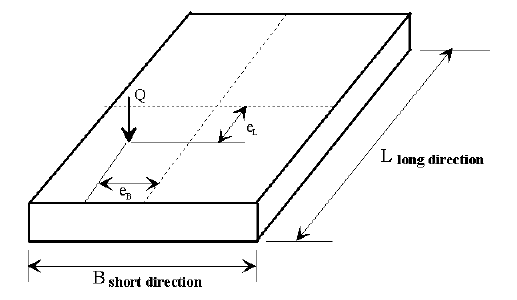
| For | For |
|---|---|
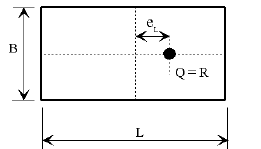
|
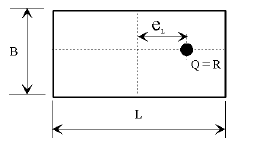
|
| Plan View | Plan View |
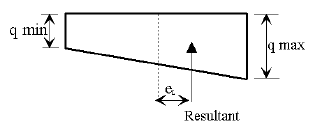
|
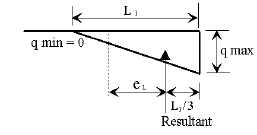
|
| Bearing Pressure | Bearing Pressure |
| CASE 1 | CASE 2 | |
|---|---|---|
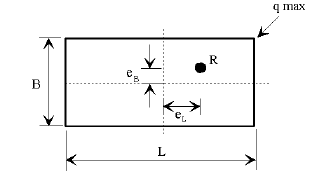
|
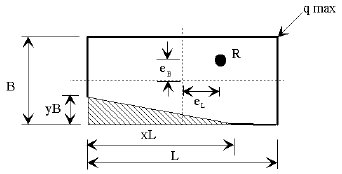
| |
| k, x and y from AASHTO chart | ||
| CASE 1 Plan View | CASE 2 Plan View | |
| CASE 3 | CASE 4 | |
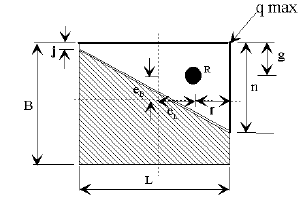
|
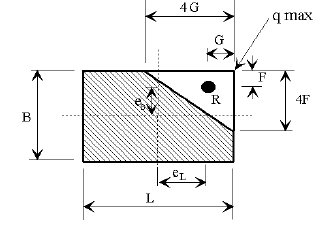
| |
| CASE 3 Plan View | CASE 4 Plan View | |
Loading Cases
Loads for Groups I thru VI shall be calculated for all bridges.
Earthquake loads shall be calculated when the bridge is in Seismic Zones B, C, and D.
Loads for other group loadings shall be used on a case by case basis.
Reinforcement
The footing is to be designed so that the shear strength of the concrete is adequate to handle the shear stress without the additional help of reinforcement. If the shear stress is too great, the footing depth should be increased.
Shear
The shear capacity of the footings in the vicinity of concentrated loads shall be governed by the more severe of the following two conditions.
Critical section at "d" distance from face of column:
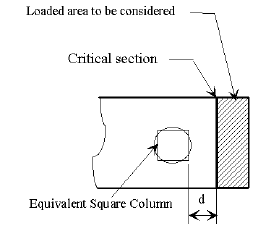
|
| Load Factor |
|---|
| = footing width |
Critical section at "d/2" distance from face of column:
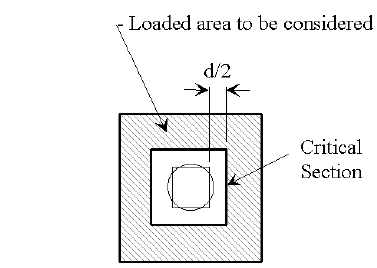
|
| Load Factor |
|---|
| If shear stress is excessive, increase footing depth. | |
Bending
If the shear line is within the projected equivalent square column, the footing may be considered satisfactory for all conditions. (minimum reinforcement required)
If the shear line is outside of the projected column, the footing must be analyzed and reinforced for bending and checked for shear stress.
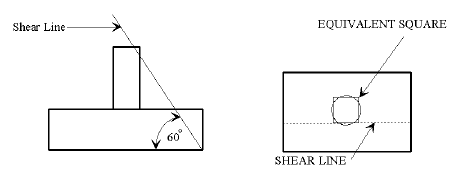
The critical section for bending shall be taken at the face of the equivalent square column. The equivalent square column is the theoretical square column which has a cross sectional area equal to the round section of the actual column and placed concentrically.
Reinforcement in Bottom of Footing
The bearing pressure used to design bending reinforcement for Group I thru VI loads shall be calculated using Load Factor Loads.
The bearing pressure used to design bending reinforcement for Earthquake Loads in Categories B, C, and D shall be calculated from the same loads as specified in AASHTO Division 1-A Seismic Design for ultimate bearing pressure.
The bottom reinforcement shall be designed using ultimate strength design.
Distribution of Reinforcement
|
| L = Footing Length |
| B = Footing Width |
Reinforcement shall be distributed uniformly across the entire width of footing in the long direction. In the short direction, the portion of the total reinforcement given by AASHTO Equation 4.4.11.2.2-1 shall be distributed uniformly over a band width equal to the length of the short side of the footing, B.
Reinforcement in Top of Footing
Reinforcement in the top of the footing shall be provided for Seismic Performance Categories B, C, and D. This reinforcement shall be the equivalent area as the bottom steel in both directions. The top steel shall be placed uniformly outside the column.
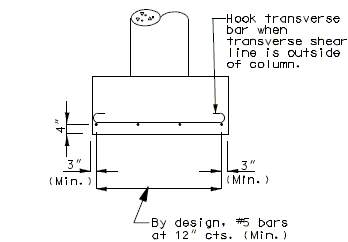
|
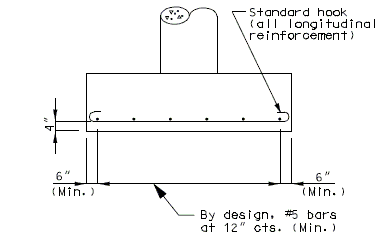
|
| Front Elevation | Side Elevation |
|---|
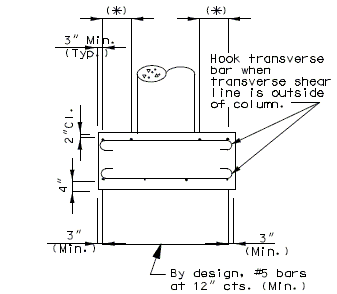
|
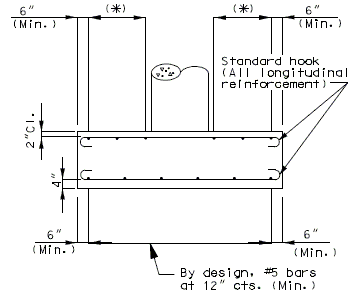
|
| Front Elevation | Side Elevation |
|---|
| (*) | Use same area of steel in the top of the footing as is required for the bottom. |
751.40.8.11.5 T- Joint Connections
Principal Tension and Compression Stresses in Beam-Column Joints
The connections where columns and beams join, or where columns and footings join, should be based on the capacity design for shear and diagonal tension. For most locations, this is a “T”-shaped joint. For the analysis of “knee joints”, see Priestley and Seible, 1996.

In the capacity design of connection joints, the column moment, M0, will be the moment that is known and which will correspond to flexural overstrength of the column plastic hinges, i.e. M0 = 1.3Mp of the column. If the columns are designed based on plastic hinging, the beam and footings shall be designed with capacities greater than or equal to 1.3Mp.
At each joint, the principal tension and compression stresses are defined and checked as follows:
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
- (7)
- (8)
- in which:
- Vjh = Average horizontal shear force within a joint.
- Vjv = Average vertical shear force within a joint.
- vjh = Average horizontal shear stress within a joint.
- vjv = Average vertical shear stress within a joint.
- hb = Beam depth.
- hc = Column diameter or rectangular column cross-section height.
- bje = The effective width of a joint, defined in Fig. 751.40.8.11.5.2.
- D = Round column diameter.
- fv = Average vertical axial stress due to column axial force Pc, including the seismic component.
- Pc = Column axial force.
- fh = Average horizontal axial stress at the center of the joint.
- pc = Nominal principal compression stress in a joint. (positive)
- pt = Nominal principal tensile stress in a joint. (negative)
- bb = Beam width
- bc = Column cross-section width
In Fig. 751.40.8.11.5.2(c), the effective width is taken at the center of the column section, allowing a 45° spread from boundaries of the column section into the beam cap. In the transverse direction, the effective width will be the smaller of the value given by eq. (3) and the beam cap width bb. Experimental evidence indicates that diagonal cracking is initiated in the joint region when psi. The principle compression stress pc shall be limited to .
Design of Reinforcement for Beam-Column Joints
When the principal tension stress, pt, exceeds psi, joint cracking occurs and the following reinforcement shall be provided:
a) Vertical beam stirrup reinforcement shall be placed throughout the distance of hb/2 from the column face on each side of the column. The required amount of vertical beam stirrup reinforcement, Ajv, is:
- (9)
- Where:
- Asc = The total area of longitudinal steel
- f°yc = overstrength stress in the column reinforcement use
- f°yc = 1.1f
- fyv = yield stress of vertical stirrup reinforcement.
b) Vertical beam stirrup reinforcement within the joint, Avi, is
- (10)
c) The additional beam bottom longitudinal reinforcement required is
- (11)
- where fyb = the yield stress of the beam bottom longitudinal reinforcement. This additional reinforcement must be carried a sufficient distance to develop its yield strength a distance hb/2 from the column face.
d) The horizontal hoop reinforcement within a joint requires
- (12)
which for F = 0 simplifies to
- (13)
- Where
- F = The beam cap prestress force.
- fyh = The yield stress of the horizontal hoops.
- La = The Anchorage length in the joint.
The minimum amount of horizontal hoop reinforcement shall be
- (14)
The spacing of the horizontal hoop can be based on:
(15)
- Where
- As = The cross-sectional area of the hoop bar.
- D’ = The hoop diameter.
When the principal tension stress, pt, does not exceed psi, no joint cracking is expected. However, the following minimum reinforcement shall be provided:
- a) Vertical beam stirrup reinforcement within the joint based on eq. (10)
- b) Minimum horizontal hoop reinforcement based on eq. (14)
Note that the bending of any hooked reinforcement outward, away from the column core, shall not be used because it directs the anchorage force away from the joint. Inward bending of the column reinforcement is allowed. However, it is likely to cause a congestion problem. The use of straight column reinforcement embedded into the beam-column joint is recommended. The standard T-joint reinforcement details are shown in Figs. 751.40.8.11.5.4 - 751.40.8.11.5.6. If any reinforcement requirement based on eqs. (9) through (14) is greater than that shown in Figs. 751.40.8.11.5.4 - 751.40.8.11.5.6, the greater requirement shall be used.
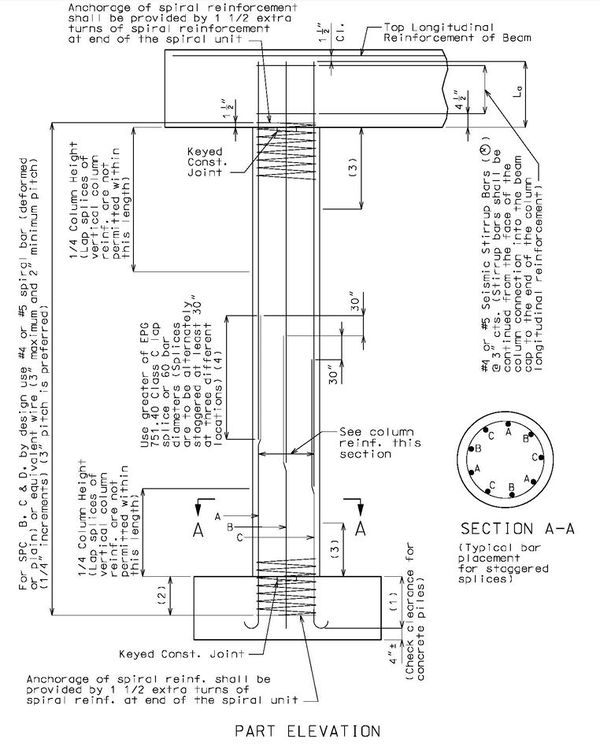
- (1) Increase by 25% the development length (other than top bars) or the standard hook in tension “Ldh” of EPG 751.40.8.4.2.
- (2) The spiral bars or wire shall be continued for a distance equal to ½ the column diameter but not less than 15” from the face of the column connection into the footing.
- (3) Use the greatest length of the following: column diameter of 1/6 of the clear height of column. Lapping of spiral reinforcement in this region is not permitted.
- (4) Splices may be eliminated when the column height is 20’-0” or less or restrictions do not practically allow for lap splices.
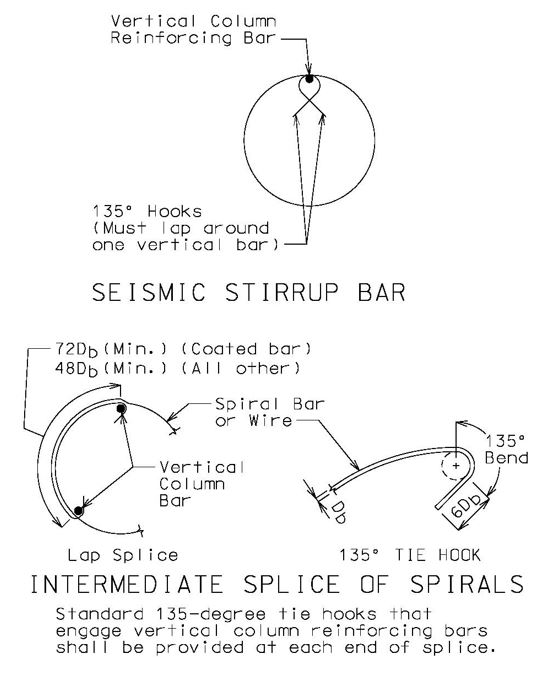
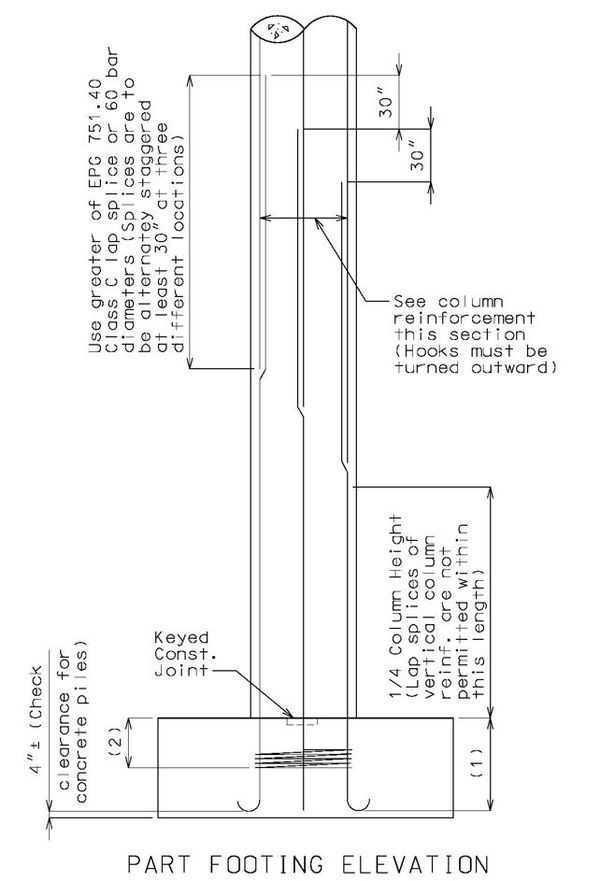
- See additional guidance in EPG 751.9.3.1.7, below, for footing reinforcement not shown.
- (1) Increase by 25% the development length (other than top bars) or the standard hook minimum in tension “Ldh” of EPG 751.40.8.4.2.
- (2) The spirals shall be continued for a distance equal to ½ the column diameter but not less than 15” from the face of the column connection into the footing.
Example 751.40.8.11.5.1: A column is subjected to an axial load (due to dead and seismic earthquake loads) of 520 kips. The column diameter is 36 in. with 20 #8 bars for longitudinal reinforcement. The beam cap dimensions are 3 ft. 9 in. wide by 3 ft. 7 in. deep with 5 #11 bars for the top reinforcement and 7 #10 bars for the bottom reinforcement as shown in Fig. 751.40.8.11.5.7. The column overstrength moment-axial load curve is shown in Fig. 751.40.8.11.5.8. Design the reinforcement details for the beam-column joint.
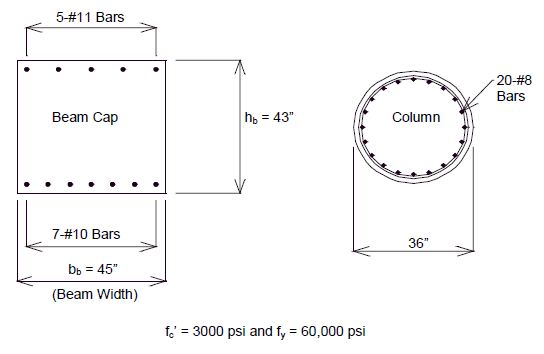
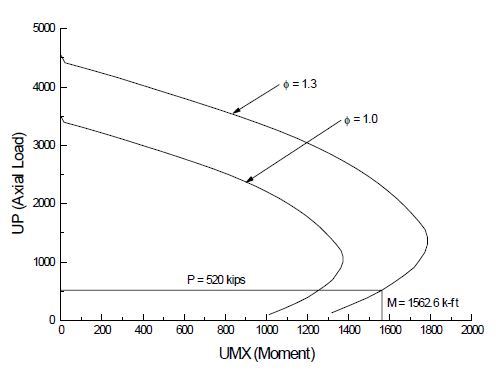
Solution:
The axial load for the column = 520 kips.
From Fig. 751.40.8.11.5.8, M0 = 1562.6 k-ft.
From eq. (1): = 436.07 kips
From eq. (3): = 45 in.
From eq. (2): = 269.18 psi.
Vertical Axial Stress:
From eq. (6):
- = 146.27 psi.
Horizontal Stress:
- fh = 0 psi.
From eq. (7):
pc = 352.07 psi ≤ 0.3(3000 psi) = 900 psi O.K.
From eq. (8):
pt = -205.80 psi ≥ 3.5 3000 = 191.7 psi Not O.K.
Since pt is greater than , special joint reinforcement based on eqs. (9) through (14) are needed.
Check if moment capacity of the beam is greater than the overstrength moment capacity of the column.
Neglect the effect of the compression steel (conservative).
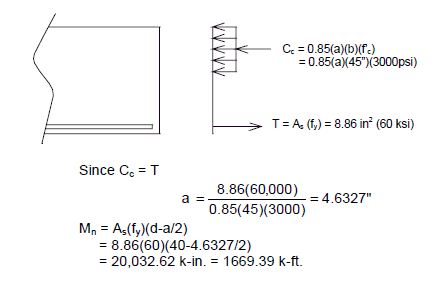
Compare moment capacity of beam versus overstrength moment capacity of the column:
- 1669.39 k-ft. > 1562.60 k-ft.
Moment capacity of beam is greater than the overstrength moment capacity of the column. O.K.
Design of reinforcement for the beam-column joint
- - Vertical reinforcement should be placed throughout a distance of hb/2 from the column face on each side of the column.
- From eq.(9):
- Asc = 15.70 in2
- From eq.(9):
- = 1.1f = 66 ksi.
- fyv = 60 ksi.
- Ajv = 0.125 (15.70) 66 / 60 = 2.16 in2
- - Reinforcement within the joint confines:
- From eq. (10):
- = 0.0625 (15.70) 66 / 60 = 1.08 in2
- From eq. (10):
- - Additional bottom of beam longitudinal reinforcement:
- From eq. (11):
- = 0.0625 (15.70) 66 / 60 = 1.08 in2
- From eq. (11):
- This reinforcement must be developed at a distance hb/2 away from the face of the column.
- - Hoop Reinforcement:
- From eq. (13):
- La = 40 in.
- fyh = 60 ksi
- ∴use ρs
- use #4 hoop reinforcement
- As = 0.1963 in2
- D’ = 36 – 2(2) – 4/8 = 31.5 in.
- ρs = 0.003238
- From eq. (15): = 7.70” spacing > 3” max. from Fig. 751.40.8.11.5.4. Therefore, Use S = 3”
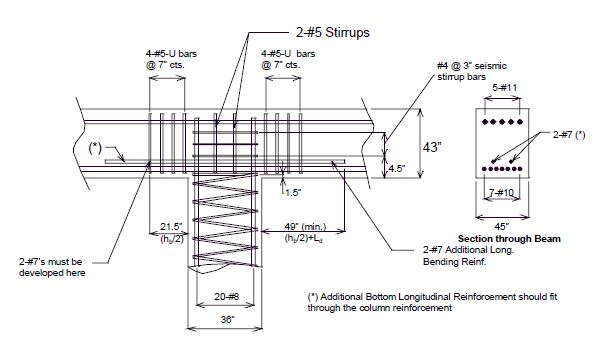
Principal Tension and Compression Stresses in Column-Footing Joints
Column – Footing joints are essentially the same as inverted beam-column T joints. Eqs. (1) through (8) are applicable to column-footing joints except the beam height, hb, shall be changed to the footing height, hf.
Design of Reinforcement for Column-Footing Joint
The design of the reinforcement for column-footing joints is similar to that for beam-column T joint. From a joint performance viewpoint, it is desirable to bend the column bars inward toward the joint by using 90° hook bars, but this will cause undue congestion. Bending column bars away from the joint will increase the diagonal tension stress within the joint region. However, it makes a stable platform for supporting the column cage and prevents congestion. When the column reinforcement is bent outward, eqs. (9) through (14) shall be applied. Since the column inelastic action may develop in directions other than parallel to one of the principal axes of the footing, the amount of vertical reinforcement in eq. (9) shall be placed in each of the four quadrant areas outside the joint. In other words, a total vertical stirrup area of:
- (16)
shall be placed around the column.
Extra top reinforcement in the footing is also required in accordance with eq. (11). This reinforcement should pass through the column reinforcement or be placed as close as possible to the sides of the column and extend a distance of not less than l = 0.5*D + Ld, where Ld is the bar development length, beyond the face on both sides of the column.
Example 751.40.8.11.5.2: A column is subjected to an axial load (due to dead and seismic loads) of 520 kips. The column diameter is 36 in. with 20 #8 bars for longitudinal reinforcement. All column reinforcement is bent outward into the footing away from the joint. The footing depth is 39 inches. The top and bottom reinforcement for the footing is shown in Fig. 751.40.8.11.5.10, below. Design the reinforcement details for the column-footing joint.
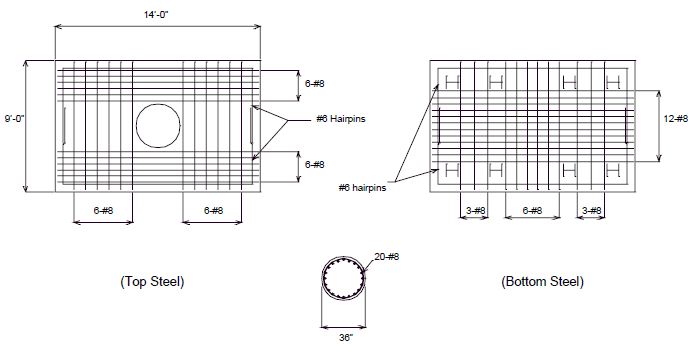
Solution:
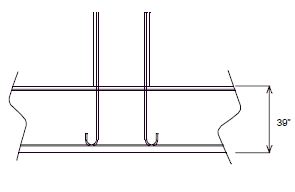
The axial load for the column = 520 kips.
From Fig. 751.40.8.11.5.8 in Example 751.40.8.11.5.1, M0 = 1562.6 k-ft.
From eq.(1): = 480.8 kips
From eq. (3):
From eq. (2): =262.39 psi.
Vertical Axial Stress:
From eq. (6):
- = 136.21psi.
Horizontal Axial Stress:
- fh = 0 psi.
Principal Stresses:
From eq. (7):
- = 339.19 psi. ≤ 0.3(3000psi.) = 900 psi. O.K.
From eq. (8):
- = -202.98 psi. > 3.5 = 191.7 psi. Not O.K.
Since pt is greater than allowed, special joint reinforcement based on eqs. (9)through (14) are needed.
Check moment capacity
Check the moment capacity of footing in the long direction to see if it is greater than the overstrength moment capacity of the column.
Neglect the effect of the compression reinforcement.
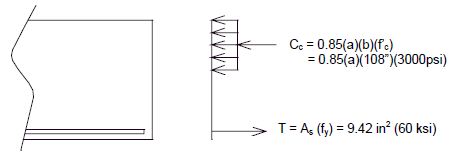
- Since Cc = T
- = 2.0523"
- Mn = As(fy)(d - a/2)
- = 9.42(60)(35-(2.0523/2))
- = 1600.17 k-ft.
Compare moment capacity of footing overstrength moment capacity of the column:
- 1600.17 k-ft > 1562.60 k-ft.
Moment capacity of the footing is greater than the overstrength moment of capacity of the column. O.K.
Check the moment capacity of the footing in the short direction to see if it is greater than the overstrength moment capacity of the column.
Neglect the effect of the compression reinforcement.
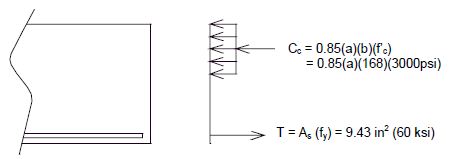
- Since Cc = T
- = 1.3207"
- Mn = As(fy)(d - a/2)
- = 9.43(60)(35-(1.3207/2))
- = 1619.11 k-ft.
Compare moment capacity of footing overstrength moment capacity of the column:
- 1619.11 k-ft > 1562.60 k-ft.
Moment capacity of the footing is greater than the overstrength moment of capacity of the column. O.K.
Design of reinforcement for the column-footing joint
- - Vertical reinforcement should be placed throughout a distance of hf/2 from the column face on each side of the column.
- From eq. (16):
- Asc = 15.71 in2
- = 1.1 fy = 66 ksi.
- fyv = 60 ksi.
- Ajv = 0.5 (15.71) (66 / 60) = 8.641 in2
- From eq. (16):
- - Reinforcement within the joint confines:
- From eqs. (9),(10) & (16):
-
- = 0.25 (15.71)(66/60) = 4.320 in2
-
- From eqs. (9),(10) & (16):
- - Additional top of footing longitudinal reinforcement:
-
- = 0.0625 (15.70)(66 / 60) = 1.08 in2
-
- This reinforcement must be developed at a distance hb/2 away from the face of the column and must be placed so that the reinforcement goes through the column reinforcement. Asb is required in both directions in the footing.
- - Hoop Reinforcement:
- From eq. (13):
- La = 35 in.
- fyh = 60 ksi
- = 0.004232
- = 0.003195
- ρs > ρs, min ∴use ρs
- Use #5 hoop reinforcement
- As = 0.3068
- D’ = 36 - 2(2) - 5/8” = 31.375”
- ρs = 0.004232
- From eq. (15): = 9.24"
- Use 9” Spacing
- Note: By adding 3 in. to footing depth in this example problem, the principal tensile stress in the joint would have been less than the maximum allowed tensile stress, thus eliminating the need for the special joint reinforcement other than the minimum required reinforcement. However, the practice of increasing footing depth to eliminate the need for the special joint reinforcement should be limited to increasing the footing depth a maximum of 6 inches.